22 几何组成分析的几个概念.

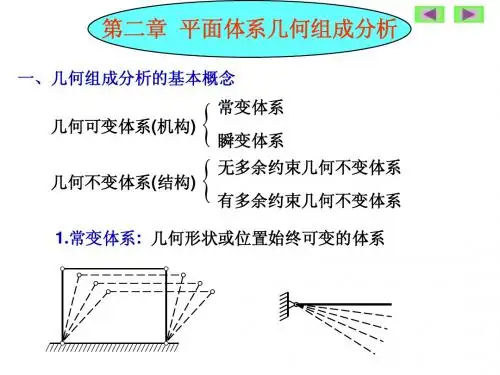
几何组成分析的几个概念1、几何不变体系与几何可变体系几何不变体系是指受到任意荷载作用下，若不考虑材料的应变，其几何形状和位置均能保持不变的体系。

几何可变体系是指即使不考虑材料的应变，在微小的荷载作用下也会产生刚体位移，而不能保持原有的几何形状和位置。

几何可变体系分为几何常变体系和几何瞬变体系。

几何可变体系在很小的荷载作用下会产生刚体位移，经微小位移后仍能继续发生刚体运动，这样的几何可变体系称为几何常变体系。

若原为几何可变体系，经微小位移后即转化为几何不变体系，这类几何可变体系称为几何瞬变体系。

工程结构绝不能采用几何瞬变体系，而且也应避免采用接近于瞬变的体系。

2、自由度指体系在所受限制的许可条件下独立的运动方式，即能确定体系几何位置的彼此独立的几何坐标数目。

平面内一点的自由度为2，一个刚片的自由度为3。

3、约束（联系）约束是指限制体系运动的各种装置，包括外部约束（支座约束）和内部约束。

（1）外部约束一个活动铰支座、固定铰支座和固定支座分别相当于1、2、3个约束。

（2）内部约束一根单链杆相当于1个约束；连接j（j>2）个结点的复链杆，相当于2j-3个单链杆，即相当于2j-3个约束；一个单铰相当于2个约束；连接m（m>2）个刚片的复铰，可折合成（m-1）个单铰，即相当于2(m-1)个约束作用；一单刚结点相当于3个约束；连接m（m>2）个刚片的刚结点称为复刚结点，可折合成（m-1）个单刚结点，即相当于3(m-1)个约束。

约束从能否减少体系的自由度方面来考虑，可分为必要约束和多余约束。

为保持体系几何不变所必须具有的约束称为必要约束，不能使体系的自由度数目减少的约束称为多余约束。

4、瞬铰（虚铰）两个刚片间用两个不共线链杆相连，其约束作用相当于这两根链杆交点位置处的一个铰所起的约束作用，这个铰称为虚铰或瞬铰（图1a）。

在几何组成分析中，尤其要注意：两刚片间用两根相互平行的链杆相连，两平行链杆所起的约束作用相当于无穷远处的瞬铰所起的约束作用，如图1b所示。

几何组成分析是结构力学中的重要内容，旨在判别体系是否为几何不变，从而决定其能否作为结构。该方法主要从约束的数量和布置方式两个方面进行分析。其中，自由度是表示体系自由运动程度的量，其数目等于决定体系几何位置的独立几何参数数目。刚片则是在平面内的刚体，一根杆件或一个几何不变部分均可看作一个刚片。约束则是能减少自由度的装置，如链杆和单铰等。平面杆件体系的自由度计算有具体的公式，如平面刚片系统的自由度计算公式－b－r。通过计算自由度，可以初步判断体系的几何性质。若自由度大于零，则体系几何可变；若自由度等于零，则体系为几何不变的必要条件，需进一步分析；若自由度小于零，则体系有多余约束，同样需进一步分析。此外，文档还介绍了复铰、复链杆等概念，并强调了计算自由度时的注意点。

3
1 2
3
A
A
1
B
2
C
3
1 2 3 1 2 3
1 2 3 1 2 3
几何常变体系
几何瞬变体系
几何瞬变体系
2.基本原则二： 三刚片组成原则 三刚片由三个不共线的铰两两相连，组成无多余约束几 何不变体系。
1.基本原则一： 二刚片组成原则
二刚片由三个不平行、不交于一点的链杆相连，组成无 多余约束几何不变体系。
虚铰
无多余约束几何不变体系
无多余约束几何不变体系
两个链杆相当于一个铰,故二刚片组成原则可改写为: 二刚片由不共线的一个铰和一个链杆相连，组成无多余约 束几何不变体系。
几何常变体系
1 2
几何瞬变体系
4.有多余约束几何不变体系: 减少一个或多个约束(链杆)仍为几 何不变的体系。
无多余约束几何不变体系
有多余约束几何不变体系
无多余约束几何不变体系 二、约束
有多余约束几何不变体系
＝
一个链杆为一个约束 一个铰链相当于两个链杆,为两个约束
虚铰 交于无穷远
＝
固定端相当于三个链杆,为三个约束
二、无多余约束几何不变体系的组成原则
无多余约束几 何不变体系
无多余约束几 何不变体系
几何瞬变体系
3.二元片理论 一个铰连接两个不共线的链杆称为二元片。 在一个体系上增加或减少一个二元片，不改 变原体系的几何组成性质。 二元片
＝
无多余约束几何不变体系
＝
有一个多余约束几何不变体系
三、刚片的划分 1. 铰接三链杆的三角形为无多余约束几何不变体系，可作为一 个刚片。在此基础上增加若干个二元片，仍为无多余约束几何不 变体系，可视作该刚片的扩大。

简单铰。
y
Ⅱ
A•
A• Ⅰ
(a)
o
x
(b)
y Ⅱ
Ⅰ
(c)
o
x
(d)
上面四图中，(a)、(b)图中A点为虚铰，(c)、(d)图中虚铰位置在无穷远处。
2020/9/17
2.2.4 必要约束和多余约束
必要约束——影响体系自由度数目增减的约束。
多余约束——不影响体系自由度数目增减的约束。
A
B
A
C
B
(a)
(b)
图（a）中，三根链杆均为必要约束。 图（b）中，横杆为必要约束，三根竖杆可任意去掉一根，为多余约束， 去掉后剩下的两根为必要约束。
2020/9/17
2.3 结构的几何组成规则
可以证明，铰接三角形为最基本的几何不变体系，且无多余约束。
C
A
B
2.3.1 点和刚片的组成规则
规则Ⅰ（二元体规则）——一点与刚片间用两根不共线的链杆相连，可
A，
有两个独立坐标 x、y，故一个点在平面内有两个自由度。
图（b）所示为平面内一个刚片由位置 A B 变为位置 A B 的情形，
这个刚片可以有 x 方向的移动（x）和 y 方向的移动（y），还可以有转
动（），由于一个刚片在平面内有三种独立的运动方式（x、y、三个独
立坐标），故一个刚片在平面内有三个自由度。
联结 n 个刚片的复铰，其作用相当于（ n -1）个简单铰。
3、固定端支座或简单刚性联结的约束作用
B
一个固定端支座相当于三个约束。
AⅠB
Ⅱ
一个刚性联结限制了三个自由度，
A
2020/9/17
故一个刚性联结相当于三个约束。

联系：限制运动的装置，又称为约束
y
1、多余联系：体系中不能减少自由度的联系
B
2、必要联系：体系中维持几何不变性所必须的联系
3、常见的联系
A 2
1
（1）链杆：两端用铰连接且不考虑自身重量的构件
o
x
一个链杆=一个联系
（四）联系
（2）单铰：只连接两个刚片的铰 一个单铰=两个联系
（3）复铰：连接两个以上刚片的铰 连接n个刚片的复铰 =(n-1)个单铰 =2(n-1)个联系
刚片：在平面上可以看作一个几何不变体系的物体
形 状 可 随 意 替 换 一根梁，一个柱子，一根链杆，地基基础，地球或体系中已经确定的几何不
变的某一部分，都可以看作一个平面刚片。
（三）自由度
自由度：确定平面体系位置所需的独立坐标的个数
y
y
x
y
O
x
一个点的自由度=2
B
xA
y
O
x
一个刚片的自由度=3
（四）联系
B
刚片Ⅲ
C
刚片Ⅰ
（二）两刚片规则
两个刚片用一个铰和一根不通过 此铰的链杆相连，组成的体系是几何 不变的，且没有多余联系。
推论2 两个刚片用三根链杆相连， 三链杆不全平行且不交于同一点，则 组成的体系是几何不变的，且没有多 余联系。
刚片Ⅱ
链杆
刚片Ⅰ
刚片Ⅱ
刚片Ⅰ
（三）二元体规则
二元体：两根不在一直线上的链杆连接 一个新结点的构造。
二元体规则：在一个体系上增加或 拆除二元体，不会改变原有体系的几何 构造性质。
A
链杆1
链杆2
刚片Ⅰ
（四）几何不变体系的基本组成规律 核心：铰接三角形规则

二、二刚片规则： 两个刚片用既不全平行也不全交于一点的 三根链杆相联，所组成的体系是几何不变 体系，且无多余约束。
O
ΙΙ
ΙΙΙ

推论： 两个刚片由一个铰和一根轴线不通过该铰的 链杆相联，所组成的体系是几何不变体系， 且无多余约束。
ΙΙ
C
A

B
例三、
C
A

分析图示体系的几何构造：
D
解法一： 1、找刚片：
依据材料概括晚清中国交通方式的特点，并分析其成因。
提示：特点：新旧交通工具并存(或：传统的帆船、独轮车， 近代的小火轮、火车同时使用)。 原因：近代西方列强的侵略加剧了中国的贫困，阻碍社会发 展；西方工业文明的冲击与示范；中国民族工业的兴起与发展；
政府及各阶层人士的提倡与推动。
[串点成面· 握全局]
（二）二元体规则：
增加或去掉二元体不改变原体系的几何
组成性质。
C
A

B
例五、 分析图示体系的几何构造：
解：
A
D
E
基本铰结三角形ABC符合 三刚片规则，是无多余约
B
束的几何不变体系；依次
C
F
G
在其上增加二元体A-D-C、
C-E-D、C-F-E、E-G-F后， 体系仍为几何不变体，且 无多余约束。
一、几何构造特性：
（一）无多余联系的几何不变体系称为静定 结构。
静定结构几何组成的特点是：
任意取消一个约束，体系就变成了
几何可变体系。
（二）有多余联系的几何不变体系称为超静 定结构。
特点： 某些约束撤除以后，剩余体系仍
为几何不变体系。
二、静力特性：
（一）静定结构： 在荷载作用下，可以依据

第二章平面杆件体系的几何组成分析杆件结构力学的任务之一就是研究结构的几何组成规律和合理形成，几何组成分析就是讨论这方面的内容。

本章从几何组成分析中相关的几个概念着手，研究平面杆件体系的几何组成规律及几何组成分析方法，并说明体系的几何组成与静定性之间的关系。

几何组成分析的主要目的是解决怎样组成的杆件体系才能承受荷载这个基本问题。

同时，由于结构的受力性能与其组成方式存在必然的联系，因此对一些较复杂的结构，可根据其几何组成特点，选择相应的计算方法和计算次序。

第一节几何组成分析的几个概念一、平面杆件体系的类型杆件结构是指由若干杆件相互连接，并与基础通过一定方式相连接而构成的结构体系。

结构受荷载作用时，杆件截面上产生应力，材料产生应变，从而结构产生变形。

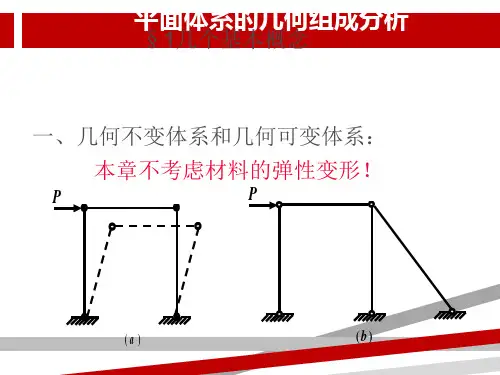
这种变形一般是很微小的，不影响结构的正常使用，因此在几何组成分析中不考虑这种由于材料应变而产生的变形。

当体系中一部分受到任意荷载作用，若不考虑材料的应变，其几何形状和位置均能保持不变，称该部分为几何不变部分，如图2-1(a)所示铰结三角形ABC为几何不变部分。

在几何组成分析中，任意一个几何不变部分都可以看作一个刚片，如一根链杆、铰接三角形ABC(图2-1(a))，甚至是支撑上部体系的基础等。

图2-1 几何不变体系与几何可变体系(a)几何不变部分（刚片）(b)几何不变体系(c)几何可变体系（几何常变）当上部体系通过一定方式与基础相连构成的整个体系，受到任意荷载作用时，若不考虑材料的应变，其几何形状和位置均能保持不变，则称该体系为几何不变体系。

如图2-1(b)所示，将铰接三角形ABC通过不相互平行也不交于一点的三根链杆与基础相连构成的杆件体系，为几何不变体系。

工程结构都应该是几何不变体系。

图2-1(c)所示三连杆体系，即使不考虑材料的应变，在微小的荷载作用下也会产生刚体位移(如图中虚线所示)，而不能保持原有的几何形状和位置，该体系称为几何可变体系。

几何可变体系有两种特殊情况。

2. 正确区分静定结构与超静定结构。
二、基本概念
1. 几何不变体系与几何可变体系
几何不变体系—若不考虑材料的应变，体系 的位置和形状不会改变。
2
几何不变体系
几何可变体系—若不考虑材料的应变，体系 的位置和形状是可以改变的。 常变体系
几何可变体系
瞬变体系
常变体系 ——可以发生大位移的几何可变体系
叫作常变体系。 3
1）链杆 简单链杆 仅连结两个结点的杆件称为简单链 杆。一根简单链杆能减少一个自由度，故一根 简单链杆相当于一个约束。yyx Nhomakorabeaφ
x
x,
链杆约束
3 2 x 1
y x
x, y,1,2,3
7
复杂链杆 连结三个或三个以上结点的杆件称 为复杂链杆，一根复杂链杆相当于（2n-3）根 简单链杆，其中n为一根链杆连结的结点数。
2. 在进行分折应时，宜先判别体系中有无二元体，如 有，则应先撤去，以使体系得到简化。
3. 如果体系仅通过三根既不完全平行，又不完全相交 的支座链杆与基础相联接的体系，则可直接分析体系内 部的几何组成。如果体系与基础相连的支座连杆数多于 三根，应把基础也看成刚片作整体分析。
4. 已知为几何不变的部分宜作为大刚片。 5. 两根链杆相当于其交点处的虚铰。 6. 运用三刚片规则时，如何选择三个刚片是关键，刚 片选择的原则是使得三者之间彼此的连接方式是铰结。
思考题： 18-3、18-4、18-7、18-8
习题：
18-24、18-26、18-27、 18-28、18-32、18-35
预习静定梁与静定刚架
36
若连结的刚片数为m，则该复杂铰相当于(m-1) 个简单铰，故其提供的约束数为2(m-1)个。

二、平面刚片系的自由度 1.平面刚片系的组成：
由刚片以一定方式相连组成
各刚片间用结点（刚结点、铰结点）相连
刚片与基础之间用支杆相连
2.刚片间连接对自由度的减少：
1）单铰：连结两个刚片的铰称为单铰 。一个单铰相当于两个 约束。
2）复铰：连结两个以上刚片的铰称为复铰。连结n 个刚片 的复铰相当于(n－1)个单铰。
A a
C
B
B
杆通过铰 瞬变体系
瞬 变 体 系 瞬 变 体 系 常 变 体 系
3、一点与一刚片用两根不共 线的链杆相联，组成无多余约束 的几何不变体系。 1 A 2
B
A
C
两根共线的链杆联一点 瞬变体系
两根不共线的链杆联 结一点称为二元体。
在一体系上增加（或减去）二元体不改变 原体系的机动性，也不改变原体系的自由度。
(平面刚片系) (平面链杆系)
计算自由度，可能出现以下三情况： ⑴ W>0 (V>0) → 存在自由度，几何可变。 ⑵ W=0 (V=0) → 约束数正好等于刚片全无联系时 的自由度。可能几何不变，但不能保证。 ⑵ W<0 (V<0) → 约束数正好大于刚片全无联系时 的自由度。体系有多余约束。
§2-3 平面几何不变体系的基本组成规则
铰
链杆
Ⅱ
铰 实铰
O
虚铰
刚片2 E B A D C 刚片1 F
C
刚片2
A
B
刚片1
D
E
说明： 1. 连接两刚片的三个链杆相交于一点， 形成瞬变体系。
实铰：几何可变
虚铰：瞬变
2. 连接两刚片的三个链杆相互平行。 ⑴三平行杆不等长，组成瞬变体系(图① )。 ⑵三平行杆等长，且在同一侧，组成几何 可变体系( 图② )。

A
O
x
一固定支座： 3个约束
三、约束（联系）
2、内部约束
y
AB
Ⅰ αβ
xC θ
Ⅱ
y O
x
自由度由6个减至5个
一根单链杆(Simple link， 连接两个铰结点的杆件) ：
n=1
y 1
23
O
x
自由度由6个减至3个
复链杆(Multiple link，连接j>2 个铰结点的杆件) ：相当于2j3个单链杆，n=2j-3
三、约束（联系） 2、内部约束
y
A
Ⅰ xBθ
α
Ⅱ
y
O
x
自由度由6个减至4个
一单铰(Simple hinge， 联结两个刚片的铰) ：
n=2
y
Ⅲ
βA
Ⅰ9个减至5个
复铰（ Multiple hinge，联结两个以 上刚片的铰）：联结m个刚片的复 铰可看成m-1个单铰，n=2(m-1)
一、平面杆件体系的分类 几何可变体系(Geometrically unstable system )
体系受到任意荷载作用，即使不考虑材料的应变，在很小的荷载 作用下也会引起体系的几何形状和位置的改变，这样的体系称为 几何可变体系。
情况I：几何常变体系(Constantly unstable system)
原为几何可变体系，经微小位移后 仍能继续发生刚体运动的几何可变 体系，称为几何常变体系。
一、平面杆件体系的分类 几何可变体系(Geometrically unstable system )
体系受到任意荷载作用，即使不考虑材料的应变，在很小的 荷载作用下也会引起体系的几何形状和位置的改变，这样的 体系称为几何可变体系。

几何组成分析几何组成分析（也称为结构几何学）是结构力学的一个重要方法，用于研究结构的形态、几何特性及其对结构力学特性的影响。

通过对结构的几何分析，可以获得结构的稳定性、刚度、位移、变形等重要信息，对结构的设计和优化具有重要意义。

几何组成分析的基本原理是根据结构的形态及其载荷情况，利用几何学的基本概念和计算方法，对结构的各个组成部分进行几何分析，并结合材料力学原理，求解结构的刚度矩阵、位移向量和变形矩阵等重要参数。

其中，结构的刚度矩阵描述结构在载荷作用下的刚度特性；位移向量表示结构在载荷作用下的位移；而变形矩阵则描述结构在载荷作用下的变化情况。

1.结构的坐标系及基本概念：建立合适的坐标系，确定结构的基本要素，如结构的节点、杆件或面坯等。

2.结构的构件模型：根据结构的具体形态和几何特性，采用适当的模型对结构的构件进行建模和描述。

3.结构的几何约束：根据结构的形态和几何特性，确定结构的几何约束条件，如节点和杆件的位移、角度等。

4.结构的刚度计算：根据结构的几何模型和几何约束条件，利用刚度法或变分原理，求解结构的刚度矩阵和刚度方程。

5.结构的位移计算：通过求解结构的刚度方程，得到结构的位移向量，描述结构在载荷作用下的位移的大小和方向。

6.结构的变形分析：根据结构的位移向量和几何约束条件，计算结构的变形矩阵，描述结构在载荷作用下的形变情况。

通过几何组成分析，可以定量描述结构的形态、几何特性及其对结构力学特性的影响。

它既可以作为结构静力分析的一种方法，用于求解结构的刚度、位移和变形等参数；也可以应用于结构动力分析，研究结构在动载荷作用下的动力响应。

几何组成分析在工程实践中具有非常重要的应用价值。

首先，它可以辅助结构工程师进行结构设计和优化，提高结构的稳定性和刚度性能。

其次，在结构检测和维修中，几何组成分析可以用于评估结构的变形和破坏情况，指导结构的维修方案和控制措施。

此外，几何组成分析还可以应用于结构材料的研究和性能表征，为结构材料的选择和设计提供科学依据。

在两刚片之间至少应该加入3个约束，才可能将这 两个刚片组成一个几何不变的体系。
下面讨论怎么布置这些约束才能达到上述目的。
一、两刚片法则
首先回顾一下铰结点的特点。
实铰
(a）
虚铰 O
刚片I
①
②
刚片II
(b）
图(b)中，刚片I和Ⅱ用两根不平行的链杆①、②联结。 若刚片I固定不动，那么刚片Ⅱ可绕两杆延长线的交点O转 动；反之，若设刚片Ⅱ固定不动，那么刚片I也可绕O点转 动。
三、二元体法则
二元体：由两根不共线的链杆联结一个新结点（特指 铰结点）的装置。
二元体
二元体法则：在一个体系上增加或者去掉一个二元体，不 会改变原体系的几何组成性质。即： 1）若原体系为几何可变体系，则增加或者去掉一个二元体 后，体系仍为几何可变体系； 2）若原体系为几何不变体系，则增加或者去掉一个二元体 后，体系仍为几何不变体系。
4、总结：静定结构、超静定结构的两种定义
• 用静力平衡条件叙述 全部反力和内力是否可以由静力平衡条件全部求得。
• 用几何组成规则叙述 静定结构：几何不变、无多余约束； 超静定结构：几何不变、有多余约束。
作业：书P.17 2-1、2-2、2-7、2-9、2-11、2-12
（a）
（b）
3、从几何组成上定义
1）静定结构：几何不变、无多余约束的体系。
凡是无多余约束的几何不变体系一定是静定结构； 反之，静定结构一定是几何不变且无多余约束的体系。
2）超静定结构：几何不变、有多余约束的体系。
凡是有多余约束的几何不变体系一定是超静定结构； 反之，超静定结构一定是几何不变且有多余约束的体系。
球或体系中已经肯定为几何不变的某个部分都可看 作一个刚片。

几何构造分析的几种常见分析思路： 几何构造分析的几种常见分析思路： 1、去除二元体，将体系化简单，然后再分析 分析实例1 A B C D E F
先去除两个二元体，然后再分析 A B C
刚片ABC由不交于同一点的三根链杆与地基刚片 相连，组成无多余约束的几何不变体系。
分析实例 2
F D D C A A B B E C E
c
(2,3)
d
(2,3)
.
(1,2) 6
e
分析实例 6
E D F D
O13
E
O12 O23
F
A A
B C
B
C
取三角形CEF、杆BD和基础为三刚片，分 、 和基础为三刚片， 取三角形 和基础为三刚片 别用链杆DE和 、 和 处支座链杆 处支座链杆、 别用链杆 和BF、AD和B处支座链杆、AE 处链杆两两构成的三虚铰O 和C处链杆两两构成的三虚铰 12，O23，O13 处链杆两两构成的三虚铰 相连，三铰不共线， 相连，三铰不共线，故体系为无多余约束的几 何不变体系。 何不变体系。
规律3：三个刚片之间用三个铰两两相连,且三个铰不在 一直线上,则组成 规律 ：
无多余约束的几何不变体系。
II
III
II
III
I
几何不变体系 4、增减二元体规则 、
I
几何瞬变体系
一体系上增加或减少若干个二元体，不改变原体系的几何组成。 二元体：两根不共线的链杆固定一个新结点的装置。如：
几何不变体系 几何不变体系
上述几个规则可归结为三角形规律
几何可变体系 几何可变体系
按组成规律结构可归结为三种基本装配格式： 按组成规律结构可归结为三种基本装配格式：
1、固定一结点的装配格式—简单装配格式 2、固定一刚片的装配格式—联合装配格式 3、固定二刚片的装配格式—复合装配格式 装配过程通常有两种 1、从基础出发构造

2.1 几何不变体系和几何可变体系
一、几何不变体系和几何可变体系
1、几何不变体系——受到任意荷载作用后，若不考虑 材料的应变，其几何形状和位置均能保持不变的体系。
D
FP A A1 弹性变形 EI FP A
几何不变体系：刚体.swf
EI1=∞
B
B
一、几何不变体系和几何可变体系
2、几何可变体系——受到任意荷载作用后，若不考虑材料 的应变，其几何形状和位置仍可以发生改变的体系。
三、体系的几何组成性质与计算自由度之间的关系
a) W=1>0 由此可知：
b) W=0
c) W=-1<0
(1) 若W＞0，体系一定是几何可变的。 (2) 若W≤0，只表明具有几何不变的必要条件，但不 是充分条件。因为体系是否几何不变还取决于约束的 布置是否合理。
2.4 平面几何不变体系的基本组成规则
(4)刚片与地基之间的固定支座和铰支座不计入g和h， 而应等效代换为三根支杆或两根支杆计入r。
【例2-1】试求图示体系的计算自由度W。
m1 m4 m7 (3)h m2 m5 (1)h m6 (3)g
(1)h m3 (3)h
m8
(3)r
m9 (3)r
m=9，g=3，h=8, r=6
W = 3m-(3g+2h+r) = 3×9-(3×3+2×8+6) = -4
图a是内部没有多余约束的 刚片，而图b、c、d则是内 部分别有1、2、3个多余约 a) 束的刚片，它们可以看作 在图a的刚片内部分别附加 了一根链杆或一个铰结或 c) 一个刚结。
b)
d)
在应用公式时，应注意以下几点：
(3)刚片与刚片之间的刚结或铰结数目（复刚结或复 铰结应折算为单刚结或单铰结数目）计入g和h。

4
二、二元体规则 二元体： 二元体： 两根不在同一直线上的链杆连结一点的装置 二元体规则： 在任一体系上增加或撤消一个二元体， 二元体规则： 在任一体系上增加或撤消一个二元体，均不会改 变原体系的几何组成性质 三、三刚片规则 三刚片用不共线的三个单铰两两相连， 三刚片用不共线的三个单铰两两相连，构成一几何不变体系 说明 （1）若三铰共线，则构成几何瞬变体系 ）若三铰共线， （2）单铰也可以是由两链杆构成的虚铰 ）
5
§2-3 静定结构和超静定结构
多余约束： 多余约束： 保证体系几何不变的前提下可以撤除的约束 静定结构： 几何不变而无多余约束的体系； 静定结构： 几何不变而无多余约束的体系； 全部支座反力和内力均可由静力平衡方程求出 超静定结构： 几何不变但有多余约束的体系； 超静定结构： 几何不变但有多余约束的体系； 支座反力和内力不可能由静力平衡方程全部求出
2
四、两种基本约束装置 约束： 限制物体位移的装置，称能够消除物体（体系） 约束： 限制物体位移的装置，称能够消除物体（体系）一个自 由度的装置为一个约束 1. 链杆 仅在两处与其他物体铰结的自重不计的刚性杆称为链杆 一根链杆为一个约束 2. 单铰 连结两个刚片的铰链称为单铰 一个单铰为两个约束，即一个单铰的约束 一个单铰为两个约束，即一个单铰的约束作用相当于两根链杆 说明： 说明： 两根链杆的约束作用可用一个位于其延长线交点处的单 铰来取代， 铰来取代，称为虚铰
3
五、几何不变体系的必要条件 加入足够多的约束消除其全部自由度
§2-2 几何不变体系的简单组成规则
一、两刚片规则 两刚片用三根不完全相交也不完全平行的链杆相连，构成一几何 两刚片用三根不完全相交也不完全平行的链杆相连， 不变体系 说明（1）三根链杆交于一点，构成几何可变体系 ）三根链杆交于一点， （2）三根链杆的延长线交于一点，构成几何瞬变体系 ）三根链杆的延长线交于一点， （3）三根链杆平行且等长，构成几何可变体系 ）三根链杆平行且等长， （4）三根链杆平行但不等长，构成几何瞬变体系 ）三根链杆平行但不等长，

第4讲几何构造分析的几个概念结构力学O O C中国大学M O O C 中国大学M O O C 中国大学M O O CO O C中国大学M O O C 中国大学M O O C 中国大学M O O CO O C中国大学M O O C 中国大学M OO C中国大学M OO CO O C中国大学MOOC 中国大学M O O C 中国大学M OO COO C中国大学M OO C 中国大学M O O C 中国大学M OO COO C中国大学M OO C中国大学M O O C中国大学M O O COO C中国大学M OO C中国大学M OO C中国大学M O O COO C 中国大学M OO C 中国大学M OO C 中国大学M O O C几何构造分析是力学计算吗？有计算公式吗？几何构造分析有什么用？自由度和约束是什么关系？O O C中国大学M O O C 中国大学M O O C 中国大学M O O CO O C中国大学M O O C 中国大学M O O C中国大学M O O CO O C中国大学M O O C中国大学M OO C中国大学M OO CO O C中国大学MOOC中国大学MO O C中国大学M OO COO C 中国大学M OO C 中国大学M OO C 中国大学M OO COOC中国大学M OOC中国大学M OO C中国大学M OO COO C中国大学M OO C中国大学M OO C 中国大学M OO COO C 中国大学M OO C 中国大学M OO C 中国大学M OO C一、几何构造分析的目的➢一个杆件结构要能够承受各种可能的荷载，它本身应是几何稳定的，即几何形状保持不变，简称几何不变体系。

➢几何构造分析的目的，就是把杆件结构看成一个杆件体系，检查它是不是几何不变体系，从而正确设计新结构。

➢也可以判定结构是静定还是超静定，如为超静定结构，还可判定其超静定次数。

O O C中国大学M O O C 中国大学M O O C 中国大学M O O C中国大学M O O C中国大学M O O C 中国大学M O O C 中国大学M O O C中国大学MO O C中国大学M O O C 中国大学M OO C中国大学M OO C中国大学MO O C中国大学MOOC 中国大学M OO C中国大学M OO C中国大学MOO C 中国大学M OO C 中国大学M OO C中国大学M OO C中国大学MOOC中国大学M OOC 中国大学M OO C中国大学M OO C中国大学MOO C中国大学M OO C 中国大学M OO C中国大学M OO C中国大学MOO C 中国大学M OO C 中国大学M OO C 中国大学M OO C中国大学M二、几何不变体系和几何可变体系➢不考虑由于材料的应变所产生的变形，即在零应变假设下（杆件假设为刚性杆件）进行几何构造分析。

Ⅰ
Ⅱ
ADC→Ⅰ，CBE→Ⅱ，ⅠⅡ用铰C和链杆DE联结满足规律2，组成一大 刚片。
上部体系与基础用3根链杆联结。 结论：体系几何不变，无多余约束。
例5：分析图示体系
• 解： • 支座杆多于3，上 部体系与基础一起分 析。 • 两点用铰与其他 部分联结的曲、直杆 均可视为链杆。 • 基础→Ⅰ， CDE→Ⅱ，两刚片用 1，2，3链杆联结。
自由度为1，可变 体系。
自由度为零，体 系可能几何不变。
例：
m = 4, n = 5 , r=3 W=3×4-(2×5+3) = - 1
有多余约束， 体系可能几何不变。
2、平面铰接体系计算公式 （研究对象：铰结点）
组成 = j 个自由的点+ b 个单链杆 + r个支座链杆 计算自由度 = j 个自由结点的自由度数 - b 个单链杆 - r个支座链杆
形状是不变的，且无多余约束。
几何组成分析时，应分清刚片（组合 刚片）和约束，所有部件使用不重复不遗 漏。注意对于某些复杂体系，基本规律不 适用。
O
Ⅱ
1 3 2
Ⅰ
由规律2，可见三杆交于 一点。
结论：几何瞬变体系。
例6(a)：分析图示体系
• 解：
用规则1，2均 不妥。 • 体系有九根杆， 规律3适用。取三根 OⅠⅡ 不相邻的链杆作刚 片，相连的三个铰 不共线。 •
Ⅰ
Ⅱ O ⅠⅢ
Ⅲ
OⅡⅢ
结论：体系内部几何不变，无多余约束。
例6(b)：分析图示体系
组成 = m个自由刚片+（ n个单铰+r个座链杆）
计算自由度= m个自由刚片的自由度数– （n个单铰+r个支座链杆）
(2-6)