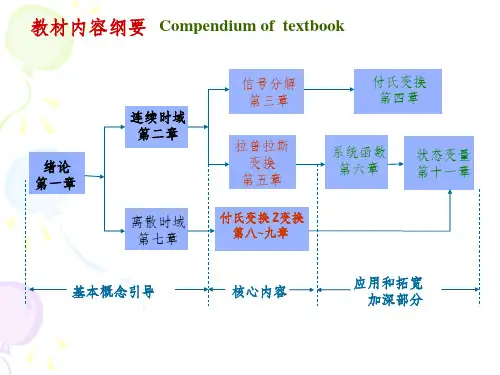
信号与线性系统课件(第5版)管致中 期末复习总结课件

四、拉普拉斯反变换由，常为s 的有理函数)()(t f s F 求)(s F 一般形式：1110111)(a s a s a s b s b s b s b s F n n n m m m m ++++++++=---- （为实数，m 、n 为整数）k k b a 、如nm ≥)()()()(s D s N s R s F +=R(s)的拉氏变换为冲激函数及其各阶导数——理想情况一般情况下：nm <求拉氏反变换有三种方法：查表、部分分式展开法和围线积分法（留数法）(一）部分分式展开法1110111)()()(a s a s a s b s b s b s b s D s N s F n n nm m mm ++++++++=---- ＝（）n m <要点：将分解，逐个求反变换，再叠加)(s F 基本形式：0,1≥↔-t e s s ts kk 1．的根无重根[的极点为单阶] 0)(=s D )(s F )1()())(()()()()(21 n s s s s s s s N s D s N s F ---=＝极零点)(s F 极点：使＝∞的s 根值，)(s F 如为的极点),,1(n k s k =)(s F 零点：使的s 根值，0)(=s F 如，)()()()(1m k z s z s z s s N ---= 为的零点),,1(m k z k =)(s F )2()(2211 nn k k s s k s s k s s k s s k s F -++-++-+-=ts n t s k t s t s n k ek e k e k e k t f +++++= 2121)(求系数的两种方法k k [方法一] （2）式两边乘以（）：k s s -nnk k k k k s s k s s k s s k s s s s k s s s F s s --++++--+--=-)()()()()(2211 令ks s =则ks s k k s F s s k =-=)]()[([方法二]用微分求])()()([lim s D s N s s k k s s k k -=→（形式）0)()]()[(lim s D ds ds N s s ds dk s s k -=→——罗彼塔法则k s s s D s N ='=])()([（))()()(])()[(s N s N s s s N s s k k +'-='-例1 求的反变换)2)(1(4)(+++=s s s s s F )(t f [为真分式，极点为实数])(s F 解：21)(321++++=s k s k s k s F 1）求：k s 2,1,0321-=-==s s s 2）求：k k 【方法一】,2])2)(1(4[01=+++==s s s s k ,3])2(4[12-=++=-=s s s s k 1])1(4[32=++=-=s s s s k 【方法二】用微分求,23)2)(1()(23s s s s s s s D ++=+=＋263)(2++='s s s D 2634)()(2+++='s s s s D s N ,2]2634[021=+++==s s s s k ,3]2634[122-=+++=-=s s s s k 1]2634[223=+++=-=s s s s k3）求：)(t f 21132)(++++=s s s s F －)()32()(2t eet f ttε--+-=例2)2)(1(795)(23+++++=s s s s s s F [为假分式，极点为实数] )(s F 解：)2)(1(32)(+++++=s s s s s F )(21s F s ++=令求的反变换：)(1s F 2112)2)(1(3)(1+-+++++=s s s s s s F ＝)()2()(21t ee tf tt ε---=求的反变换：)(s F )()2()(2)()()(2)()(21t e e t t t f t t t f t t εδδδδ---++'=++'=例3 求的反变换52)(2++=s s s s F [为真分式，极点为共轭复数] )(s F 解：【方法一】2211)(ss k s s k s F -+-=2令21j s --=*=s2）求：k k 1)]()[(11s s s F s s k =-=)2(41j +=2)]()[(22s s s F s s k =-=)2(41j -=*=1k 3）求：)(t f t s t s e k e k t f 2121)(+=tj t j e j ej )21()21()2(41)2(41--+--++=)](2)[(212222t j t j tj t j t e e j e e e ----++=)222(21t Sin t Cos e t -=-,2212t Sin e t Cos e t t---=0≥t ),,,()(2121k k s s f t f =tj tj ejc c ejc c t f )(21)(21)()()(βαβα-+-++=)(221t Sin c t Cos c e tββα-=)(,,,21t f c c 求→βα【方法二】为二次多项式)(s D 52)(2++=s s s D 4)1(2++=s ])[(22βα+-=s 4)1()(2++=s s s F ]2)1(2[212)1(12222++-+++=s s s tCos e s s t022)(ωωααα↔+--t Sin e s t02020)(ωωαωα↔+-1--t t2．当＝0有重根的情况[有多重极点])(s D )(s F 设＝0共有n 个根，其中一个根s 1为p 重根，其余为单根（异根）)(s D 即)())(()()(211n p p ps s s s s s s s s D ----=++ )1(][])()()([)()()(11111211211)1(111 n n p p p p p p s s k s s k s s k s s k s s k s s k s D s N s F -++-+-+-++-+-==++--令异根项][11nn p p s s k s s k -++-++ )()(00s D s N =其系数的求法如上所述重根项的求取111,,k k p （1）求：p k 1)2()()(])()()([)(00111211211)1(111 s D s N s s k s s k s s k s s k s F p p p p+-+-++-+-=--式（2）乘以，ps s )(1-)()()()()()()()(00111111221)1(1111s D s N s s k s s k s s k s s k s F s s pp p p p p-+-+-++-+=---- 再令s s =p（2）求（系数）11)1(1,k k p -引入)()()(11s F s s s F p-=）（4)()()()()()(100111121)2(11)1(11 p p p p p s s s D s N s s k s s k s s k k -+-++-+-+=---将式（4）对s 取导一次：）（5])()()([)()1()(2)(10021111)2(1)1(11 pp p p s s s D s N ds d s s k p s s k k ds s dF -+--++-+=---1])([1)1(1s s p dss dF k =-=将式（5）对s 取导一次，再令得1s s =1])([21212)2(1s s p dss F d k =-=一般情况：1,,1,,])([)!(1111 -=-==--p p k dss F d k p k s s kp kp k 总结：)()(])()()([)(001111)1(12112111s D s N s s k s s k s s k s s k s F pp p p +-+-++-+-=-- ∑-+++++=n t s t s p p ts t s t s q ek e t k e t k te k e k t f 112131111)(例求的反变换22)5)(3(52)(++++=s s s s s F 解：0)5)(3()(2=++=s s s D ⎩⎨⎧-=-=523121s s 重根个单根)1()5(53)(222211 +++++=s k s k s k s F 1）求系数22211,,k k k 单根项2)]()3[(31=+=-=s s F s k 重根项5221)]()5([-=+=s s F s dsd k 52]}352[{-=+++=s s s s ds d 1-=求式代入的另法：把)1(,22121k k k 5)5(1032)(212+++-+=s k s s s F 551032535)0(2122k F +-=⨯=121-=k 2) 求：)(t f )()102()(553t teeet f tttε-----=10)]()5[(5222-=+=-=s s F s k（二）围线积分法（留数法）拉氏反变换：⎰∞+∞-=j j stdse s F j tf σσπ)(21)(留数定理：∑⎰==ni icstsds e s F j 1Re )(21π上式左边的积分是在s 平面内沿一不通过被积函数极点的封闭曲线C 进行的，右边则是在此围线C 中被积函数各极点上留数之和。

第1章　绪　论1.1 说明波形如图1-1所示的各信号是连续信号还是离散信号。

图1-1答：连续时间信号是指它的自变量（时间变量t ）是连续的，若时间变量的取值是离散的，则为离散时间信号。

图1-1中，（a ）、（b ）、（d ）、（e ）是连续信号，而（c ）、（f ）是离散信号。

1.2 说明下列信号是周期信号还是非周期信号。

若是周期信号，求其周期T 。

（a ）t b t a 3sin sin -（b ）tb t a 7cos 4sin +（c ）141.33,cos 3sin a ≈≈+πππ和t b t （d ）t b t ππ2sin cos a +（e ）7sin 56cos 25sina tc t b t ++（f ）22sin a ）（t （g ）2)5sin 2sin (a t b t +提示：如果包含有个不同频率余弦分量的复合信号是一个周期为的周期信号，则n T 其周期必为各分量信号周期（＝1,2,3，……，）的整数倍。

即有＝或T i T i n T i m i T 。

式中为各余弦分量的角频率，i i m ωω=2i iT πω=＝为复合信号的基波频率，为正整数。

ω2Tπi m 因此只要找到个不含整数公因子的正整数使成立，就可判n 123m m m 、、、……、n m 定该信号为周期信号，其周期为：2i i iiT m t m πω==如复合信号中某两个分量频率的比值为无理数，则无法找到合适的；，该信号常称m 为概周期信号。

概周期信号是非周期信号，但如选用某一有理数频率来近似表示无理数频率，则该信号可视为周期信号。

所选的近似值改变，则该信号的周期也随之变化。

例如1.41，则可求得＝100，＝141，该信号的周期cos t+≈1m 2m 为＝200 1.414，则该信号的周期变为2000。

T π≈π答：（a ）sint 、sin3t 的角频率之比，因此该信号为周期信号，其周期为πωπ221111===m T m T （b ）sin4t 、sin7t 的角频率之比，因此该信号为周期信号，周期。