(完整版)导数与函数图像问题

高中数学导数与函数图像的关系分析与讲解在高中数学中，导数与函数图像是密不可分的。

导数是函数在某一点上的变化率，而函数图像则是函数在整个定义域上的变化规律的图形表示。

理解导数与函数图像之间的关系对于学习和应用数学知识都具有重要意义。

本文将通过具体的题目举例，分析导数与函数图像的关系，并给出解题技巧和使用指导。

一、导数与函数图像的关系导数与函数图像之间有着密切的联系。

函数的导数可以帮助我们确定函数图像的特征，如函数的增减性、极值点、拐点等。

下面通过几个具体的题目来说明导数与函数图像的关系。

例题1：已知函数$f(x)=x^3-3x^2+2x+1$，求函数在$x=1$处的导数。

解析：首先我们需要求出函数$f(x)$的导函数$f'(x)$。

根据导函数的定义，我们可以得到$f'(x)=3x^2-6x+2$。

然后，我们将$x=1$代入导函数中，得到$f'(1)=3(1)^2-6(1)+2=-1$。

这个结果告诉我们，在$x=1$处，函数$f(x)$的导数为-1。

通过这个例题，我们可以看出，函数$f(x)$在$x=1$处的导数为-1。

这意味着函数$f(x)$在$x=1$处的斜率为-1，即函数图像在该点的切线的斜率为-1。

这个信息可以帮助我们更好地理解函数图像的特征。

例题2：已知函数$g(x)=x^2-2x$，求函数$g(x)$的极值点。

解析：为了求函数$g(x)$的极值点，我们需要先求出函数$g(x)$的导函数$g'(x)$。

根据导函数的定义，我们可以得到$g'(x)=2x-2$。

然后，我们令$g'(x)=0$，得到$2x-2=0$，解得$x=1$。

这意味着函数$g(x)$的导数在$x=1$处为0，即函数图像在该点的切线的斜率为0。

通过这个例题，我们可以看出，函数$g(x)$的极值点出现在$x=1$处。

这个点处的切线斜率为0，意味着函数图像在该点处有一个极值。

这个极值可以是最大值或最小值，需要通过进一步的分析来确定。

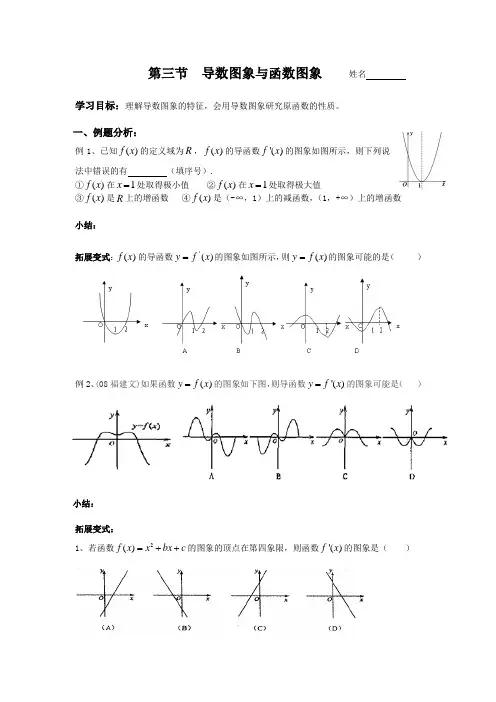
第三节 导数图象与函数图象 姓名学习目标：理解导数图象的特征，会用导数图象研究原函数的性质。

一、例题分析：例1、已知()f x 的定义域为R ，()f x 的导函数'()f x 的图象如图所示，则下列说法中错误的有 （填序号）.①()f x 在1x =处取得极小值 ②()f x 在1x =处取得极大值 ③()f x 是R 上的增函数 ④()f x 是（-∞，1）上的减函数，（1，+∞）上的增函数小结：拓展变式：)(x f 的导函数=y )('x f 的图象如图所示，则)(x f y =的图象可能的是（ ）例2、(08福建文)如果函数()y f x =的图象如下图，则导函数'()y f x =的图象可能是（ ）小结：拓展变式：1、若函数2()f x x bx c =++的图象的顶点在第四象限，则函数'()f x 的图象是（ ）2、函数()y f x =的图象过原点且它的导函数'()g f x =的图象是如图所示的一条直线，则()y f x =图象的顶点在第 象限.3、(07浙江)设()f x '是函数()f x 的导函数，将()y f x =和()y f x '=的图象画在同一个直角坐标系中，不可能正确的是（ ）例3、()f x 的导函数'()f x 的图象如右图所示，则()f x 的图象只可能是（ ）（A ） （B ） （C ） （D ）小结：拓展变式：1、(08全国卷Ⅰ文2)汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程s 看作时间t 的函数，其图象可能是( )2、已知函数()y f x =,()y g x =的导函数的图象如下图，那么()y f x =,()y g x =的图象可能是（ ）。

1.已知函数x x a x f ln )21()(2+-=.（R a ∈）（Ⅰ）当1=a 时，求)(x f 在区间[1，e ]上的最大值和最小值；（Ⅱ）若在区间（1，+∞）上，函数)(x f 的图象恒在直线ax y 2=下方，求a 的取值范围．解析：（Ⅰ）当1=a 时，x x x f ln 21)(2+=，xx xx x f 11)(2+=+='；………………2分对于∈x [1，e ]，有0)(>'x f ，∴)(x f 在区间[1，e ]上为增函数，…………3分∴21)()(2max ee f x f +==，21)1()(min ==f x f .……………………………4分（Ⅱ）令x ax x a ax x f x g ln 2)21(2)()(2+--=-=，则)(x g 的定义域为（0，+∞）.……………………………………………5分在区间（1，+∞）上，函数)(x f 的图象恒在直线ax y 2=下方等价于0)(<x g 在区间（1，+∞）上恒成立.∵xx a x xax x a xa x a x g ]1)12)[(1(12)12(12)12()(2---=+--=+--='① 若21>a ，令0)(='x g ，得极值点11=x ，1212-=a x ，………………6分当112=>x x ，即121<<a 时，在（2x ，+∞)上有0)(>'x g ，此时)(x g 在区间(2x ，+∞)上是增函数，并且在该区间上有)(x g ∈()(2x g ，+∞)，不合题意；………………………………………7分当112=<x x ，即1≥a 时，同理可知，)(x g 在区间(1，+∞)上，有)(x g ∈()1(g ，+∞)，也不合题意；………………………………………9分② 若21≤a ，则有012≤-a ，此时在区间(1，+∞)上恒有0)(<'x g ，从而)(x g 在区间(1，+∞)上是减函数；……………………………………11分 要使0)(<x g 在此区间上恒成立，只须满足021)1(≤--=a g 21-≥⇒a ，由此求得a 的范围是[21-，21].综合①②可知，当a ∈[21-，21]时，函数)(x f 的图象恒在直线ax y 2=下方.……12分2．已知函数()∈--=b a bx ax x x f ,(ln 2R ，且)0≠a .（1）当2=b 时，若函数()x f 存在单调递减区间，求a 的取值范围； （2）当0>a 且12=+b a 时，讨论函数()x f 的零点个数.解：（1）当2=b 时，函数()x f x ax x 2ln 2--=，其定义域是()∞+,0，∴()xx axax xx f1222212'-+-=--=.函数()x f 存在单调递减区间，∴()xx axx f1222'-+-=0≤在()∞+∈,0x 上有无穷多个解.∴关于x 的不等式01222≥-+x ax 在()∞+∈,0x 上有无穷多个解. ① 当0>a 时，函数1222-+=x ax y 的图象为开口向上的抛物线， 关于x 的不等式01222≥-+x ax 在()∞+∈,0x 上总有无穷多个解. ② 当0<a 时，函数1222-+=x ax y 的图象为开口向下的抛物线，其对称轴为01>-=a x .要使关于x 的不等式01222≥-+x ax 在()∞+∈,0x 上有无穷多个解. 必须480a ∆=+>，解得12a >-，此时102a -<<.综上所述，a 的取值范围为()1(,0)0,2-+∞ .另解：分离系数：不等式01222≥-+x ax 在()∞+∈,0x 上有无穷多个解， 则关于x 的不等式221212(1)1x a xx-≥=--在()∞+∈,0x 上有无穷多个解，∴21a >-，即12a >-，而0a ≠.∴a 的取值范围为()1(,0)0,2-+∞ .（2）当12b a =-时，函数()x f ()2ln 12x ax a x =---，其定义域是()∞+,0，∴()()2'12(12)1212ax a x fx ax a xx+--=---=-.令()0'=x f，得22(12)10ax a x x+--=，即22(12)10ax a x +--=，(1)(21)0x ax -+=， 0x > ，0a >，则210ax +>，∴1x = 当<<x 01时，()0'>x f；当>x 1时，()0'<x f.∴函数()x f 在区间()0,1上单调递增，在区间()1,+∞上单调递减. ∴当1x =时，函数()x f 取得最大值，其值为()1ln 1121f a b a a a =--=--+=-. ① 当1a =时，()10f =，若1≠x , 则()()1f x f <, 即()0<x f .此时，函数()x f 与x 轴只有一个交点，故函数()x f 只有一个零点； ② 当1a >时，()10f >，又()011112111ln 122<-⎪⎭⎫⎝⎛--=⨯--⎪⎭⎫ ⎝⎛⋅-=⎪⎭⎫ ⎝⎛a a a a a a e e a e a e a e e f ，()()()02121ln 2<---=---=e e ae e a aee ef ，函数()x f 与x 轴有两个交点，故函数()x f 有两个零点；③ 当01a <<时，()10f <，函数()x f 与x 轴没有交点，故函数()x f 没有零点. 3．已知函数.)(,ln )(x x g x x f ==（Ⅰ）若1>x ，求证：)11(2)(+->x x g x f ；（Ⅱ）是否存在实数k ，使方程k x f x g =+-)1()(2122有四个不同的实根？若存在，求出k 的取值范围；若不存在，说明理由.解：（I ）令,1)1(2ln )11(2)()(+--=+--=x x x x x g x f x F则222)1()1()1()1(2)1(21)(+-=+--+-='x x x x x x xx F ， ------4分因.0)(,1>'∴>x F x 故函数),1()(+∞在x F 上是增函数.又1)(=x x F 在处连续，所以，函数),1[)(+∞在x F 上是增函数.1>∴x 时，).11(2)(.0)1()(+->=>x x g x f F x F 即 ------7分（Ⅱ）令=+-=+-='=+-=+-=2322222112)(,).1ln(21)1()(21)(xx x xx x x h k y x x x f x g x h 由.1,1,0,0)(,1)1)(1(2-=='+-+x x h xx x x 则令 ------9分当x 变化时，)(x h '、)(x h 的变化关系如下表：据此可画出)(x h 的简图如下， ------12分 故存在)0,2ln 21(-∈k ，使原方程有4个不同实根. ------14分4．已知函数()()()⎪⎩⎪⎨⎧>-≤+=.01,03123x e x mx x x f x（1）当0≤x 时，函数()x f 在()()1,1--f 处的切线方程为013=+-y x ，求m 的值；（2）当0>x 时，设()1+x f 的反函数为()x g 1-（()x g 1-的定义域即是()1+x f 的值域）.证明:函数()()x gx x h 131--=在区间()3,e 内无零点，在区间()2,3e 内有且只有一个零点；（3）求函数()x f 的极值.（本小题主要考察分段函数、函数与方程、函数导数、函数的极值、函数图象的切线等知识，考查化归与转化、分类与整合、函数与方程的数学思方法，以及抽象概括能力、推理论证能力、运算求解能力和创新意识） 解:（1）当0≤x 时，()2331mx x x f +=，()311-=-m f ， ……1分()mx x x f 22+='，()m f 211-=-'，……2分函数()x f 在()()1,1--f 处的切线方程为:()()12131+-=⎪⎭⎫⎝⎛--x m m y ， ……3分 整理得:()032363=-+--m y x m ，所以有⎩⎨⎧=-=-132163m m ，解得.31=m ……4分(2) 当0>x 时，()x e x f =+1， 所以()()1ln 1>=-x x x g ，……5分()()x g x x h 131--==()1ln 31>-x x x ，()xx xx h 33131-=-='，令0)(>'x h 得3>x ；令0)(<'x h 得31<<x ，令0)(='x h 得3=x ，故知函数)(x h 在区间)3,1(上为减函数，在区间),3(+∞为增函数，在3=x 处取得极小值, 进而可知()x h 在()3,e 上为减函数，在()2,3e 上为增函数，在3=x 处取得极小值.……6分 又 ()023)(,03ln 13,013)(22>-=<-=<-=ee h h e e h .……7分所以，函数()()x gx x h 131--=在区间()3,e 内无零点，在区间()2,3e 有且只有一个零点.……8分(3)当0>x 时，()1-=x e x f 在()+∞,0上单调递增，且()1-=x e x f >0. ……9分 当0≤x 时，()()m x x mx x x f 222+=+='. ①若(),0,02≥='=x x f m 则()331x x f =在(]0,∞-上单调递增,且()0313<=x x f .又()00=f ，()x f ∴在R 上是增函数，无极值. ……10分 ②若0<m ，()()0222>+=+='m x x mx x x f ，则()2331mx x x f +=在(]0,∞-上单调递增.同理,()x f 在R 上是增函数，无极值. ……11分③若0>m ，()(),222m x x mx x x f +=+='令()0='x f ，得0,221=-=x m x .当m x 2-<时， ()0>'x f 当02<<-x m 时， ()0<'x f 所以,()2331mx x x f +=在(]m 2,-∞-上单调递增,在(]0,2m -上单调递减.又()x f 在()+∞,0上单调递增,故()[](),00==f x f 极小()[]()3342m m f x f =-=极大.……13分综上, 当0>m 时,()[](),00==f x f 极小()[]234m x f =极大.当0≤m 时, ()x f 无极值. ……14分5. 如图是函数y =f (x )的导函数y =f ′(x )的图象,则下面判断正确的是A.在区间(－2,1)内f (x )是增函数B.在(1,3)内f (x )是减函数C.在(4,5)内f (x )是增函数D.在x =2时,f (x )取到极小值 分析:本题主要考查函数的单调性、极值、最值与导函数的关系.解:在(－2,1)上,导函数的符号有正有负,所以函数f (x )在这个区间上不是单调函数;同理,函数在(1,3)上也不是单调函数.在x =2的左侧,函数在(－23,2)上是增函数,在x =2的右侧,函数在(2,4)上是减函数,所以在x =2时,f (x )取到极大值;在(4,5)上导数的符号为正,所以函数在这个区间上为增函数.答案:C6．函数a ax x y +-=23在)1,0(内有极小值，则实数a 的取值范围为（ ） A.(0,3) B. )3,(-∞ C. ),0(+∞ D. )23,0(解析： 32,023)('2a x a x x f ±==-=，由题意知只要230,1320<<<<a a 即选D7.（1992全国卷）等差数列{}n a 中，312a =，12130,0S S ><。

在微积分中，导数是一个至关重要的概念。

它提供了函数在不同点上的斜率或变化率的信息。

函数的图像则是通过绘制函数的曲线来呈现函数的全貌。

本文将探讨导数与函数图像之间的密切关系。

首先，我们来回顾一下导数的定义。

对于一个给定的函数f(x)，在点x处的导数可以通过以下公式计算得到：f'(x) = lim(h->0) [f(x+h) - f(x)] / h导数的几何解释是函数在该点的切线的斜率。

这意味着如果我们在点(x, f(x))处绘制切线，那么切线的斜率就是导数f'(x)。

根据这个定义，我们可以得出一些与函数图像有关的结论。

首先，导数提供了函数图像的局部信息。

通过计算导数，我们可以了解函数曲线在特定点的陡峭程度。

如果导数为正，那么函数曲线在该点上升；如果导数为负，那么函数曲线在该点下降。

导数的绝对值表示曲线的斜率的大小，即曲线的陡峭程度。

因此，导数可以帮助我们确定函数曲线在特定点的行为。

其次，导数提供了函数图像的全局信息。

通过计算导数，我们可以确定函数曲线在整个定义域内的变化规律。

如果导数始终为正，那么函数曲线将一直上升；如果导数始终为负，那么函数曲线将一直下降。

导数为零的点则表示函数曲线的极值点或拐点。

通过分析函数的导数，我们可以推断函数的整体行为，包括最大值、最小值和凹凸性等。

此外，导数还可以用于绘制函数的图像。

绘制函数的图像是通过连接许多点来得到的。

这样做的问题是，我们只能得到离散的点，而无法得到具体点之间的信息。

然而，通过计算导数，我们可以得到函数在每个点的斜率。

这些斜率可以帮助我们绘制更平滑的曲线，而不是简单地连接离散点。

因此，导数在绘制函数图像时起到了至关重要的作用。

最后，我们要注意到导数并不是函数图像的一切。

有些函数可能在某些点上没有导数，即导数不存在。

例如，函数在某些点上可能有间断或不可导的奇点。

在这种情况下，导数无法提供关于函数图像的任何信息。

因此，在分析函数图像时，我们应该综合考虑导数以及函数的其他特性。

导数中的图像关系问题一、常见基本题型：（1）已知图像交点个数，求参数的取值范围，例1. 已知3x =是函数2()16ln(1)10f x x x x =++-的一个极值点．(1)求函数()f x 的单调区间；(2)若直线y b =与函数()y f x =的图像有三个交点，求b 的取值范围．解：(1) f (x )＝16ln(1＋x )＋x 2－10x ，x ∈(－1，＋∞)， 2243()1x x f x x-+'=+. 当x ∈(－1,1)∪(3，＋∞)时，()0f x '>；当x ∈(1,3)时，()0f x '<.∴()f x 的单调增区间是(－1,1)，(3，＋8)；()f x 的单调减区间是(1,3)，（2）由(1)知()f x 在(－1,1)单调增加，在(1,3)单调减小，在(3，＋∞)上单调增加，且当x ＝1，或x ＝3时，f ′(x )＝0，∴f (x )的极大值为f (1)＝16ln2－9，极小值为f (3)＝32ln2－21.∵f (16)＞162－10×16＞16ln2－9＝f (1)， f (e －2－1)＜－32＋11＝－21＜f (3)，∴在f (x )的三个单调区间(－1,1)，(1,3)，(3，＋∞)，直线y ＝b 与y ＝f (x )的图像各有一个交点，即f (3)＜b ＜f (1)．∴b 的取值范围为(32ln2－21,16ln2－9).例2.已知函数))(1ln()(2R a x a ax x x f ∈---=（1）当1=a 时，求函数)(x f 的最值；（2）说明是否存在实数)1(≥a a 使)(x f y =的图象与2ln 85+=y 无公共点. 解：（1）函数))(1ln()(2R a x a ax x x f ∈---=的定义域是（1，+∞）当a=1时，1)23(21112)('--=---=x x x x x x f ， 所以)(x f 在)23,1(为减函数，在),23(+∞为增函数，所以函数)(x f 的最小值为2ln 43)23(+=f .（2）1≥a 时，由（1）知)(x f 在（1，+∞）的最小值为2ln 14)22(2a a a a f -+-=+， 令2ln 14)22()(2a a a a f a g -+-=+=在［1，+∞）上单调递减， 所以2ln 43)1()(max +==g a g ，则,081)2ln 85()(max >=+-a g 因此存在实数)1(≥a a 使)(x f 的最小值大于2ln 85+，故存在实数)1(≥a a 使y=)(x f 的图象与y=2ln 85+无公共点.(2)已知图像的位置关系求参数的取值范围例 3.已知二次函数2()(0)h x ax bx c c =++>，其导函数()y h x '=的图象如图所示，()ln ()f x x h x =-．若函数2ln y x x =-, ([1,4])x ∈的图象总在函数()y f x =的图象的上方，求c 的取值范围．解：由题意可知，2x －ln x >x 2－3x －c ＋ln x 在x ∈[1,4]上恒成立，即当x ∈[1,4]时，c >x 2－5x ＋2ln x 恒成立设g (x )＝x 2－5x ＋2ln x ，x ∈[1,4]，则c >g (x )max .易知()g x '=＝2x －5＋2x ＝2x 2－5x ＋2x =(21)(2)x x x--. 令()0g x '=得，x ＝12或x ＝2. 当x ∈(1,2)时，()0g x '<，函数()g x 单调递减；当x ∈(2,4)时，()0g x '>，函数()g x 单调递增．而g (1)＝12－5×1＋2ln 1＝－4，g (4)＝42－5×4＋2ln 4＝－4＋4ln 2，显然g (1)<g (4)，故函数g (x )在[1,4]上的最大值为g (4)＝－4＋4ln 2，故c >－4＋4ln 2. ∴c 的取值范围为(－4＋4ln 2，＋∞)．二、针对性练习1．已知函数21()ln 12f x x x =+-.，求证：在区间(1,)+∞上，函数()f x 的图象在函数 32()3g x x =的图象的下方. 证明：令2312()()()ln 123F x f x g x x x x =-=+-- 则2322112(1)(1)'()2x x x x x F x x x x x x+--++=+-== ∵当1x >时'()0F x <，∴函数()F x 在区间(1,)+∞上为减函数∴12()(1)1023F x F <=--< 即在(1,)+∞上，()()f x g x <∴在区间(1,)+∞上，函数()f x 的图象在函数32()3g x x =的图象的下方。

函数与导数的关系总结在微积分中，函数和导数是密切相关的概念。

导数是描述函数变化率的工具，它提供了函数在任意点附近的局部信息。

本文将总结函数与导数之间的关系，包括导数的定义、导数与函数图像的关系、导数的性质以及函数与导数的应用等内容。

一、导数的定义函数的导数是指函数在某一点的变化率，用极限来定义。

设函数f(x)在点x0处的导数为f'(x0)，则导数的定义如下：f'(x0) = lim┬(h→0)⁡〖(f(x0+h)-f(x0))/h〗二、导数与函数图像的关系函数的导数能够提供函数图像的许多重要信息。

根据导数的正负和大小，可以分析函数的增减性、极值点和拐点。

具体而言：1. 当导数大于0时，函数递增；2. 当导数小于0时，函数递减；3. 导数为0的点可能是函数的极值点或拐点。

三、导数的性质1. 常数导数性质：若c为常数，则(d/dx)(c) = 0，即常数函数的导数为0；2. 线性运算：若f(x)和g(x)都可导，且k为常数，则(d/dx)(k*f(x)) = k*(d/dx)(f(x))，(d/dx)(f(x)+g(x)) = (d/dx)(f(x))+(d/dx)(g(x))；3. 乘积法则：若f(x)和g(x)都可导，则(d/dx)(f(x)*g(x)) = f'(x)*g(x) + f(x)*g'(x)；4. 商法则：若f(x)和g(x)都可导，且g(x)≠0，则(d/dx)(f(x)/g(x)) =(f'(x)*g(x)-f(x)*g'(x))/[g(x)]^2。

四、函数与导数的应用函数的导数在实际问题中有许多应用。

以下是几个常见的应用情景：1. 切线与法线：函数在某一点的导数即为该点的切线斜率，通过导数可以求解切线和法线的方程；2. 极值问题：通过导数的符号变化，可以分析函数的极值点；3. 函数图像的绘制：通过导数的信息，可以确定函数图像的变化趋势和关键特征。

函数与导数图象关系问题解析在数学中，函数的概念是一个数学模型，通过它来解释实物中的某种变化，是一个客观存在的、抽象的数学概念。

通过某种算法表达，可以把函数表示出以图像形式，这种表示图像就是函数图象。

函数图象有多种表示形式，如折线图、曲线图和平面图等。

此外，由于函数的特性，有些函数的图象可以用极坐标表示，又称极坐标图。

不管用什么方式，函数图象里有两个重要的变量，一是它的函数值，即横坐标和纵坐标，表示函数值与它的参数之间的关系；二是函数的导数值，即曲线上每一点表示它相对于函数参数的变化率，也就是函数图象的斜率。

函数及其导数图象之间有着密切的联系，通过图象可以直观地看出函数及其导数之间的关系。

把函数图象和它的导数图象画在一起，可以更清楚地看出函数及其导数的关系，从而更深入地了解它们之间的关系。

例如，一次函数的图象为一条直线，它的导数的图象是一条平行于它的直线，两条直线的斜率分别为函数的常数和函数的导数，其它高阶函数的图像同理，其曲线的斜率也可以用函数的导数来表示。

一般来说，函数和导数图像之间的关系可以总结为：导数图像是函数图像斜率的图像，函数图像是导数图像反斜率的图像。

因此，不论函数是什么形式，都可以从它的导数来求得，从而知道它的形式。

另外，通过函数图象其导数图象可以推断出函数的最大值、最小值及极值的位置等信息，比如函数的凹凸性、分段处的断点，以及函数的增减性，等等。

也就是说，在研究函数特性时，函数图象和导数图象是分不开的，都是必不可少的。

从以上可以看出，函数及其导数图象之间有着十分密切的关系，只有通过综合分析，才能准确估计函数的参数，才能对函数的性质有更深入的了解。

因此，运用函数及其导数图象解决数学问题，成为数学中一个重要的内容。

综上所述，函数及其导数图象的关系是理解函数的性质和推断函数的参数的重要内容，是数学学习者必须掌握的基本技能。

因此，当学习数学的时候，要多多加强对函数及其导数图象关系的探究，从而更好地理解函数的特性，加深对数学的理解。

导数与函数图像的关系分析导数是微积分中的重要概念，它描述了函数在某一点的变化率。

而函数图像则是函数在平面上的可视化展示。

导数与函数图像之间存在着密切的关系，通过对导数与函数图像的分析，我们可以深入理解函数的性质与行为。

一、导数的定义与计算方法导数的定义是函数在某一点的变化率，可以通过极限的概念进行定义。

对于函数f(x)，其在点x处的导数可以表示为f'(x)，即f'(x) = lim Δx→0 (f(x+Δx) - f(x))/Δx。

这个定义可以理解为当Δx趋近于0时，函数在x点附近的变化率。

计算导数的方法有多种，其中最常见的是使用导数的基本公式。

对于常见的函数类型，我们可以通过这些公式来计算导数。

例如，对于多项式函数f(x) = ax^n，其中a为常数，n为整数，其导数为f'(x) = anx^(n-1)。

对于指数函数f(x) = e^x，其导数为f'(x) = e^x。

对于对数函数f(x) = ln(x)，其导数为f'(x) = 1/x。

二、导数与函数的增减性导数与函数的增减性密切相关。

通过导数的正负可以判断函数在某一点的增减性。

当导数大于0时，函数在该点上是递增的；当导数小于0时，函数在该点上是递减的；当导数等于0时，函数在该点上取得极值。

通过导数与函数的增减性，我们可以推导出函数的极值点和拐点。

当函数的导数从正变为负时，函数在该点上取得极大值；当函数的导数从负变为正时，函数在该点上取得极小值。

而函数的拐点则是导数的变号点，即导数从正变为负或从负变为正的点。

三、导数与函数的凹凸性导数还可以用来判断函数的凹凸性。

通过导数的二阶导数可以判断函数的凹凸性。

二阶导数表示导数的导数，可以表示为f''(x)。

当二阶导数大于0时，函数在该点上是凹的；当二阶导数小于0时，函数在该点上是凸的；当二阶导数等于0时，函数在该点上可能是拐点。

通过导数与函数的凹凸性，我们可以推导出函数的凹凸区间和拐点。

1．利用导数判断函数的单调性的方法：如果函数()y f x =在x 的某个开区间内，总有()0f x '>，则()f x 在这个区间上是增函数；如果函数()y f x =在x 的某个开区间内，总有()0f x '<，则()f x 在这个区间上是减函数． 2．利用导数研究函数的极值：已知函数()y f x =，设0x 是定义域内任一点，如果对0x 附近的所有点x ，都有0()()f x f x <，则称函数()f x 在点0x 处取极大值，记作0()y f x =极大．并把0x 称为函数()f x 的一个极大值点． 如果在0x 附近都有0()()f x f x >，则称函数()f x 在点0x 处取极小值，记作0()y f x =极小．并把0x 称为函数()f x 的一个极小值点．极大值与极小值统称为极值．极大值点与极小值点统称为极值点． 3．求函数()y f x =的极值的方法：第1步 求导数()f x '；第2步 求方程()0f x '=的所有实数根；第3步 考察在每个根0x 附近，从左到右，导函数()f x '的符号如何变化．如果()f x '的符号由正变负，则0()f x 是极大值；如果由负变正，则0()f x 是极小值．如果在()0f x '=的根0x x =的左右侧，()f x '的符号不变，则0()f x 不是极值．4．函数()f x 的最大（小）值是函数在指定区间的最大（小）的值．求函数最大（小）值的方法：第1步 求()f x 在指定区间内所有使()0f x '=的点；第2步 计算函数()f x 在区间内使()0f x '=的所有点和区间端点的函数值，其中最大的为最大值，最小的为最小值．题型一：原函数与导函数的图象【例1】 函数()f x 的导函数图象如下图所示，则函数()f x 在图示区间上（ ）O yxB ．有三个极大值点，两个极小值点C ．有两个极大值点，两个极小值点D ．有四个极大值点，无极小值点【例2】 函数()f x 的定义域为开区间()a b ，，导函数()f x '在()a b ，内的图象如图所示，则函数()f x 在开区间()a b ，内有极小值点（ ）．3个 D ．4个baOyx【例3】 ()f x '的图象不过第几象限?典例分析【例4】 若函数2()f x x bx c =++的图象的顶点在第四象限，则函数()f x '的图象可能为（ ）D.C.B.A.【例5】 汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程s 看作时间t 的函数，其图象可能是（ ）D.C.B.A.ss【例6】 设()f x '是函数()f x 的导函数，()y f x '=的图象如下图所示，则()y f x =的图象可能是（ ）A.【例7】 已知函数()f x 的导函数()f x '的图象如右图所示，那么函数()f x 的图象最有可能的是（ ）【例8】 已知函数()y xf x '=的图象如右图所示（其中()f x '是函数()f x 的导函数），下面四个图象中()y f x =的图象大致是（ ）-1-2-1211OyxD.C.B.A.-1-2-2-121O yx2112xyO 12-1-2-2-112xyO 12-1-2-2-1-1-2-2-121O yx21【例9】 ()f x '是()f x 的导函数，()f x '的图象如图所示，则()f x 的图象只可能是（ ）2xO222D.C.B.A.OxOx x OOx y【例10】 如果函数()y f x =的图象如图，那么导函数()y f x '=的图象可能是（ ）xyy=f(x)D【例11】设()f x'是函数()f x的导函数，将()y f x=和()y f x'=的图象画在同一个直角坐标系中，不可能正确的是（）【例12】如图所示是函数()y f x=的导函数()y f x'=图象，则下列哪一个判断可能是正确的（）)为增函数B．在区间(03)，内()y f x=为减函数C．在区间(4)+∞，内()y f x=为增函数D．当2x=时()y f x=有极小值【例13】如果函数()y f x=的导函数的图象如图所示，给出下列判断：函数()y f x=在区间13,2⎛⎫--⎪⎝⎭内单调递增；②函数()y f x=在区间1,32⎛⎫-⎪⎝⎭内单调递减；③函数()y f x=在区间(4,5)内单调递增；④当2x=时，函数()y f x=有极小值；⑤当12x=-时，函数()y f x=有极大值；则上述判断中正确的是___________．【例14】 函数321()2f x x x =-+的图象大致是 （ ） DC BA 1xyyxyxyxOOO O【例15】 已知函数的图像如下图所示，则其函数解析式可能是（ ）A ．()2ln f x x x =+B ．()2ln f x x x =-C ．()ln f x x x =+D ．()ln f x x x =-yx1O【例16】 函数2()(2)e xf x x x =-的图象大致是 （ ）DCBA y yyyxxxxOOOO【例17】 如图，一个正五角星薄片（其对称轴与水面垂直）匀速地升出水面，记t 时刻五角星露出水面部分的图形面积为()()()00S t S =，则导函数()y S t '=的图像大致为（ ）【例18】 函数22x y x =-的图像大致是（ ）【例19】 已知函数()f x 的导函数()f x '的图象如图所示，那么函数()f x 的图象最有可能的是（ ）【例20】 已知R 上可导函数)(x f 的图象如图所示，则不等式0)()32(2>'--x f x x 的解集为（ ）A ．(,2)(1,)-∞-+∞B ．(,2)(1,2)-∞-C ．(,1)(1,0)(2,)-∞--+∞D ．(,1)(1,1)(3,)-∞--+∞-2-121Oyx【例21()32f x ax bx c =++()f x '的图象如图所示，则函数()f x 的极小值是（ ）A ．a b c ++B ．84a b c ++C ．32a b +D ．c21Oyx题型二：函数的单调性【例22】 函数214y x x =+的单调增区间为（）A ．(0)+∞， B ．12⎛⎫+∞ ⎪⎝⎭，C ．(1)-∞-， D ．12⎛⎫-∞- ⎪⎝⎭， 【例23】 下列函数中，在区间(1)+∞，上为增函数的是（）A ．21xy =-+ B ．1xy x=- C ．2(1)y x =-- D ．12log (1)y x =-【例24】 函数()ln (0)f x x x x =>的单调递增区间是 ．【例25】 三次函数3()1y f x ax ==-在()-∞+∞，内是减函数，则（ ）A ．1a =B ．2a =C ．0a ≤D ．0a < 【例26】 函数2()(1)f x x x =-的单调递减区间是________．【例27】 函数32()31f x x x =-+是减函数的区间为（ ）A ．(2)+∞，B ．(2)-∞，C ．(0)-∞，D ．(02)， 【例28】 函数cos sin y x x x =-在下面哪个区间内是增函数（ ）A ．π3π22⎛⎫ ⎪⎝⎭，B ．(π2π)，C ．3π5π22⎛⎫⎪⎝⎭， D ．(2π3π)，【例29】 若y ax =与by x=-在()0+∞，上都是减函数，对函数3y ax bx =+的单调性描述正确的是（ ）A ．在()-∞+∞，上是增函数 B ．在()0+∞，上是增函数 C ．在()-∞+∞，上是减函数 D ．在()0-∞，上是增函数，在()0+∞，上是减函数 【例30】 函数()()()321483f x ax a x b x b =+-+-+的图象关于原点中心对称，则()f x （ ）A ．在⎡-⎣上为增函数B ．在⎡-⎣上为减函数C ．在)⎡+∞⎣上为增函数，在(-∞-，上为减函数D ．在(-∞-，上为增函数，在)⎡+∞⎣上为减函数 【例31】 若32()(0)f x ax bx cx d a =+++>在R 上是增函数，则（ ）A ．240b ac -≥B ．240b ac -≤C ．230b ac -≥D ．230b ac -≤【例32】 若21()ln(2)2f x x b x =-++在(1)-+∞，上是减函数，则b 的取值范围是（ ）A ．[1)-+∞，B ．(1)-+∞，C ．(1]-∞-，D ．(1)-∞-，【例33】 函数()21x f x x =-（ ）A ．在()02，上单调递减B ．在()0-∞，和()2+∞，上单调递增 C ．在()02，上单调递增D ．在()0-∞，和()2+∞，上单调递减 【例34】 若函数()221xf x x=-+，则()f x （ ） A ．在()-∞+∞，单调增加 B ．在()-∞+∞，单调减少C ．在(11)-，单调减少，在(1)-∞-，与(1)+∞，上单调增加D ．在(11)-，单调增加，在(1)-∞-，与(1)+∞，上单调减少【例35】 已知函数321()53f x x x ax =++-，若()f x 的单调递减区间是(31)-，，则a 的值是 ．【例36】 已知函数321()53f x x x ax =++-，若()f x 在[1)+∞，上是单调增函数，则a 的取值范围是 ．【例37】 已知321(2)33y x bx b x =++++是R 上的单调增函数，则b 的取值范围是（ ）A ．1b <-或2b >B ．1b -≤或2b ≥C ．12b -<<D ．12b -≤≤【例38】 若函数()23k kh x x x =-+在(1,)+∞上是增函数，则实数k 的取值范围是（ ）A ．[2,)-+∞B ．[2,)+∞C ．(,2]-∞-D ．(,2]-∞【例39】 已知()23k kh x x x =-+，()()ln g x h x x =+，且()g x 在(1,)+∞上是增函数，则此时实数k 的取值范围是______．【例40】 若函数32()1f x x ax =-+在(02)，内单调递减，则实数a 的取值范围是（ ） A ．3a ≥ B ．3a = C ．3a ≤ D ．03a << 【例41】 若函数32()1f x x ax =-+的单调递区间为(02)，，则实数a 的取值范围是（ ）A ．3a ≥B ．3a =C ．3a ≤D ．03a <<【例42】 已知函数232()43f x x ax x =+-在区间[]11-，上是增函数，则实数a 的取值范围为______． 【例43】 若函数232()43f x x ax x =+-在区间(2)-∞-，与(2)+∞，上都是减函数，则实数a 的取值范围为______．【例44】 函数214y x x=+的单调增区间为（ ）A ．(0,)+∞B ．1,2⎛⎫+∞⎪⎝⎭ C ．(,1)-∞- D ．1,2⎛⎫-∞- ⎪⎝⎭【例45】 对于R 上可导的函数()f x ，若满足(1)()0x f x '-≥，则必有（ ）A ．(0)(2)2(1)f f f +<B ．(0)(2)2(1)f f f +≤C ．(0)(2)2(1)f f f +≥D ．(0)(2)2(1)f f f +>【例46】 已知函数()f x 是偶函数，在()0,+∞上导数()f x '0>恒成立，则下列不等式成立的是（ ）Ａ．()()()312f f f -<-< B ．()()()123f f f -<<- C ．()()()231f f f <-<- D ．()()()213f f f <-<-【例47】 )(x f 是定义在(0,)+∞上的非负可导函数，且满足()()0xf x f x '+≤，对任意正数,a b ，若a b <，则必有（ ）A ．()()af a bf b ≤B ．()()bf b af a ≤C ．()()af b bf a ≤D ．()()bf a af b ≤【例48】 设()f x 、()g x 是R 上的可导函数，()f x '、()g x '分别是()f x 、()g x 的导函数，且()()()()0f x g x f x g x ''+<，则当a x b <<时，有（ ）A ．()()()()f x g x f b g b >B ．()()()()f x g a f a g x >C ．()()()()f x g b f b g x >D ．()()()()f x g x f a g a >【例49】 函数()()ln 1f x x ax =+-在()12，上单调递增，则实数a 的取值范围是 ． 【例50】 已知函数()321f x x ax x =-+--在()-∞+∞，上是单调函数，则实数a 的取值范围是（ ）A ．(()3-∞+∞，， B ．⎡⎣C ．(()3-∞+∞，，D ．(【例51】 若函数32()1f x x x mx =+++是R 上的单调函数，则实数m 的取值范围是（ ）A ．1(,)3+∞ B ．1(,)3-∞ C ．1[,)3+∞ D ．1(,]3-∞【例52】 已知对任意实数x 有()()f x f x -=-，()()g x g x -=，且0x >时，()0f x '>，()0g x '>，则0x <时（ ）A ．()0f x '>，()0g x '>B ．()0f x '>，()0g x '<C ．()0f x '<，()0g x '>D ．()0f x '<，()0g x '<【例53】 已知函数()21()ln 202f x x ax x a =--≠存在单调递减区间，求a 的取值范围．【例54】 设函数2()ln(1)f x x b x =++，其中12b >，判断函数()f x 在定义域上的单调性．【例55】 已知函数32()(1)(2)f x x a x a a x b =+--++()a b ∈R ，．若函数()f x 在区间(11)-，上不单调．．．，求a 的取值范围． 【例56】 函数325y ax x x =-+-在区间()-∞+∞，上单调递增，求a 的取值范围．【例57】 已知函数21()2(02]f x ax x x=-∈，，，若()f x 在(01]x ∈，上是增函数，求a 的取值范围． 【例58】 设a 为实数，函数()()3221f x x ax a x =-+-在()0-∞，和()1+∞，都是增函数，求a 的取值范围．【例59】 已知函数26()ax f x x b-=+的图象在点(1(1))M f --，处的切线方程为250x y ++=． ⑴求函数()y f x =的解析式；⑵求函数()y f x =的单调区间．【例60】 已知函数()2ln f x x x =-．⑴写出函数()f x 的定义域，并求其单调区间；⑵已知曲线()y f x =在点()()00x f x ，处的切线是2y kx =-，求k 的值．【例61】 已知函数22()ln axf x x e=-，(,a e ∈R 为自然对数的底数）． ⑴求函数()f x 的递增区间；⑵当1a =时，过点()()0,P t t ∈R 作曲线()y f x =的两条切线，设两切点为()()()11122212,(),,()P x f x P x f x x x ≠，求证：120x x +=．【例62】 已知函数x ax x x f ln 1)(2-++-=．⑴当3a =时，求函数()f x 的单调递增区间；⑵若)(x f 在区间10,2⎛⎫⎪⎝⎭上是减函数，求实数a 的取值范围． 【例63】 已知函数()ln xf x x=．⑴判断函数()f x 的单调性；⑵若()1y xf x x=+的图像总在直线y a =的上方，求实数a 的取值范围； ⑶若函数()f x 与()1263m g x x x =-+的图像有公共点，且在公共点处的切线相同，求实数m 的值．【例64】 已知函数2()ln(1)2kf x x x x =+-+（0k ≥）．⑴当2k =时，求曲线()y f x =在点()()1,1f 处的切线方程；⑵求()f x 的单调区间．【例65】 设函数32()91(0)f x x ax x a =+--<，若曲线()y f x =的斜率最小的切线与直线126x y +=平行，求：⑴a 的值；⑵函数()f x 的单调区间．【例66】 设a ∈R ，函数()()()()2121ln 1f x x a x =--+-+．⑴若函数()f x 在点()()00f ，处的切线方程为41y x =-，求a 的值； ⑵当1a <时，讨论函数()f x 的单调性．【例67】 已知函数321()32a a f x x x xb +=-++，其中a ，b ∈R ． ⑴若曲线()y f x =在点(2(2))P f ，处的切线方程为54y x =-，求函数()f x 的解析式；⑵当0a >时，讨论函数()f x 的单调性．【例68】 设函数()()e 0kx f x x k =≠．⑴ 求曲线()y f x =在点()()00f ，处的切线方程； ⑵ 求函数()f x 的单调区间；⑶ 若函数()f x 在区间()11-，内单调递增，求k 的取值范围．【例69】 已知32()f x ax bx cx d =+++是定义在R 上的函数，其图象交x 轴于A ，B ，C 三点，若点B的坐标为(20)，，且()f x 在[10]-，和[45]，上有相同的单调性，在[02]，和[45]，上有相反的单调性．⑴求c 的值；⑵在函数()f x 的图象上是否存在一点00()M x y ，，使得()f x 在点M 处的切线的斜率为3b ?若存在，求出点M 的坐标；若不存在，说明理由．【例70】 已知函数22()(1)x bf x x -=-，求导函数()f x '，并确定()f x 的单调区间．。

完整版)导数与极值、最值练习题三、知识新授一）函数极值的概念函数极值指的是函数在某个点上的最大值或最小值，包括极大值和极小值。

二）函数极值的求法：1）确定函数的定义域，并求出函数的导数f'(x)；2）解方程f'(x)=0，得到方程的根x（可能不止一个）；3）如果在x附近的左侧f'(x)>0，右侧f'(x)<0，则f(x)是极大值；反之，则f(x)是极小值。

题型一图像问题1、函数f(x)的导函数图像如下图所示，则函数f(x)在图示区间上（）第二题图）A．无极大值点，有四个极小值点B．有三个极大值点，两个极小值点C．有两个极大值点，两个极小值点D．有四个极大值点，无极小值点2、函数f(x)的定义域为开区间(a，b)，导函数f'(x)在(a，b)内的图像如图所示，则函数f(x)在开区间(a，b)内有极小值点（）A．1个B．2个C．3个D．4个3、若函数f(x)=x+bx+c的图像的顶点在第四象限，则函数f'(x)的图像可能为（）图略）4、设f'(x)是函数f(x)的导函数，y=f'(x)的图像如下图所示，则y=f(x)的图像可能是（）图略）A。

B。

C。

D。

5、已知函数f(x)的导函数f'(x)的图像如右图所示，那么函数f(x)的图像最有可能的是（）图略）6、f'(x)是f(x)的导函数，f'(x)的图像如图所示，则f(x)的图像只可能是（）图略）A。

B。

C。

D。

7、如果函数y=f(x)的图像如图，那么导函数y=f'(x)的图像可能是（）图略）ABCD8、如图所示是函数y=f(x)的导函数y=f'(x)图像，则下列哪一个判断可能是正确的（）图略）A．在区间(-2,0)内y=f(x)为增函数B．在区间(0,3)内y=f(x)为减函数C．在区间(4,+∞)内y=f(x)为增函数D．当x=2时y=f(x)有极小值9、如果函数y=f(x)的导函数的图像如图所示，给出下列判断：①函数y=f(x)在区间(-3,-1/2)内单调递增；②函数y=f(x)在区间(-1/2,2)内单调递减。

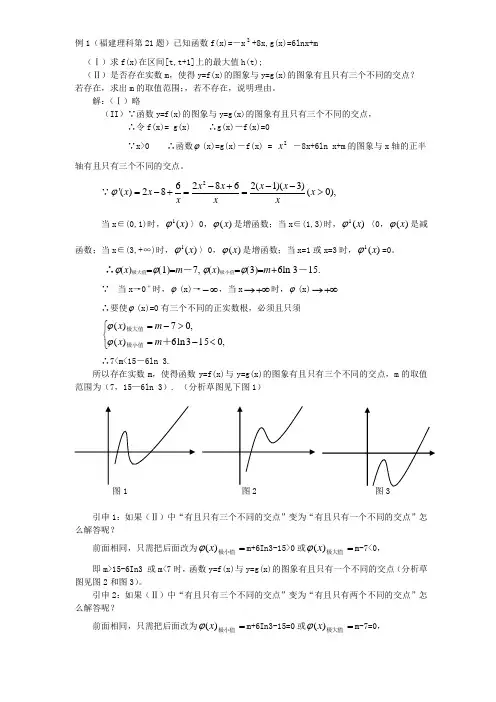
例1（福建理科第21题）已知函数f(x)=－x 2+8x,g(x)=6lnx+m（Ⅰ）求f(x)在区间[t,t+1]上的最大值h(t);（Ⅱ）是否存在实数m ，使得y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点？ 若存在，求出m 的取值范围；，若不存在，说明理由。

解：（Ⅰ）略（II ）∵函数y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点，∴令f(x)= g(x) ∴g(x)－f(x)=0∵x>0 ∴函数ϕ(x)=g(x)－f(x) = 2x－8x+6ln x+m 的图象与x 轴的正半轴有且只有三个不同的交点。

∵262862(1)(3)'()28(0),x x x x x x x x x xϕ-+--=-+==> 当x ∈(0,1)时，)(1x ϕ〉0，)(x ϕ是增函数；当x ∈(1,3)时，)(1x ϕ〈0，)(x ϕ是减函数；当x ∈(3,+∞)时，)(1x ϕ〉0，)(x ϕ是增函数；当x=1或x=3时，)(1x ϕ=0。

∴ϕ(x )极大值=ϕ(1)=m －7, ϕ(x )极小值=ϕ(3)=m+6ln 3－15.∵当x →0+时，ϕ(x)→∞-，当x +∞→时，ϕ(x)+∞→ ∴要使ϕ(x)=0有三个不同的正实数根，必须且只须⎩⎨⎧<-=>-=,0153ln 6)(,07)(＋极小值极大值m x m x ϕϕ ∴7<m<15－6ln 3.所以存在实数m ，使得函数y=f(x)与y=g(x)的图象有且只有三个不同的交点，m 的取值范围为（7，15—6ln 3）. （分析草图见下图1）图1 图引申1：如果（Ⅱ）中“有且只有三个不同的交点”变为“有且只有一个不同的交点”怎么解答呢？前面相同，只需把后面改为=极小值)(x ϕm+6In3-15>0或=极大值)(x ϕm-7<0，即m>15-6In3 或m<7时，函数y=f(x)与y=g(x)的图象有且只有一个不同的交点（分析草图见图2和图3）。

利用导数探究函数图像的交点问题在解决函数图像的交点问题时，导数起到了关键的作用。

导数能够帮助我们确定函数的变化趋势以及判断图像是否与坐标轴相交。

本文将通过一些具体的例子，来说明如何利用导数来探究函数图像的交点问题。

首先，我们来考虑一个简单的例子：求解函数y=x^2-1与x轴的交点。

我们首先将函数y=x^2-1代入x轴方程y=0，得到方程x^2-1=0。

然后我们可以通过求解这个方程来找到函数与x轴的交点。

为了更方便地解决这个问题，我们可以先求出函数的导数,即y'=2x。

然后，我们观察到导数的符号与函数的增减性息息相关。

根据导数的定义，当x>0时，导数y'>0，表示函数在该区间上是递增的。

当x<0时，导数y'<0，表示函数在该区间上是递减的。

当x=0时，导数y'=0，表示函数在该点取得极值。

综上所述，函数在x<0递减，在x>0递增，并在x=0处取得极值。

而函数y=x^2-1在x<0时，函数值始终小于0，因此不存在交点。

而在x>0时，函数值始终大于0，同样不存在交点。

所以，函数y=x^2-1不与x轴相交。

接下来，我们考虑一个稍复杂一些的例子：求解函数y=x^3-2x与y=x图像的交点。

同样地，我们先求出函数的导数，即y'=3x^2-2、然后我们观察导数的符号。

当x<-√(2/3)时，导数y'<0，表示函数在该区间上是递减的。

当-√(2/3)<x<√(2/3)时，导数y'>0，表示函数在该区间上是递增的。

当x>√(2/3)时，导数y'>0，表示函数在该区间上是递增的。

接下来，我们观察函数在极值点处的行为。

我们可以通过对导数y'=3x^2-2=0求解来找到极值点的横坐标。

解这个方程可以得到两个解：x=-√(2/3)和x=√(2/3)。

我们可以将这两个值代入原函数求解对应的纵坐标。

函数图像和导数的关系函数是数学中的一个重要概念，被广泛运用于各个领域，包括物理、经济学、生物学等。

而在研究函数时，导数是一个关键性的概念。

本文将探讨函数图像和导数的关系。

1. 函数图像的概念在数学中，函数是将一个变量的值映射到另一个变量的值的规则。

在二维平面上，我们可以用函数图像来更好地表示一个函数。

函数图像就是将函数的值在平面坐标系中表示出来的图形。

比如，y=x^2就是一个简单的函数，它的函数图像是一条抛物线。

函数图像可以帮助我们更好地理解一个函数的特点。

比如，从函数图像上我们可以看出一个函数的单调性、最值、奇偶性等。

2. 导数的概念导数是微积分中的一个概念，是描述一个函数变化率的工具。

一个函数的导数可以理解为在某一点上函数图像的切线的斜率。

它是一个数学上非常重要的概念，因为很多实际问题都需要用到导数来求解。

导数的公式是f'(x) = lim (f(x+∆x) - f(x))/∆x，其中lim代表着当∆x趋近于0时的极限值。

这个公式可以用来求出某一点上的导数值。

3. 函数图像和导数是密不可分的。

通过对函数图像的观察，我们可以大概的推测出它的导数在各个点上的趋势。

比如，对于y=x^2的函数图像，我们可以看出它在x=0的时候是处于最低点的，所以它的导数在这个点上应该是0。

而在x<0的时候，函数图像是下凹的，说明导数是负数；而在x>0的时候，函数图像是上凸的，说明导数是正数。

这个趋势可以通过计算导数值来进一步验证。

相反，导数也可以帮助我们更好地理解一个函数的图像。

一个函数的导数为0的点，对应着函数图像上的拐点或者极值。

通过计算导数，我们可以精确地找出这些关键点。

4. 总结函数图像和导数是数学中两个非常重要的概念。

它们不仅可以帮助我们理解一个函数的特点，还可以互相帮助来进一步加深我们的理解。

通过掌握函数图像和导数的关系，我们可以更好地应用函数这一概念来解决实际问题。

导数与函数的像变化一、导数的概念导数是微积分中的重要概念，用来描述函数在某一点的变化率。

对于函数 f(x)，当 x 沿着自变量的方向发生微小变化Δx 时，函数值 f(x) 也发生相应的微小变化Δf。

若Δf/Δx 在Δx 趋于零的极限存在，我们称之为函数 f(x) 在点 x 处的导数，记作 f'(x) 或 dy/dx。

二、导数的几何意义导数的几何意义可以通过斜率来理解。

在平面直角坐标系上，取函数 f(x) 上两点 A(x, f(x)) 和B(x+Δx, f(x+Δx))，则直线 AB 的斜率可以表示函数在这两点间的平均变化率。

而导数 f'(x) 表示的是函数在某一点x 处的瞬时变化率，即取点 A 为极限，使得Δx 趋于零，此时直线 AB 的切线斜率就等于导数 f'(x)。

三、导数的计算方法导数的计算可以通过极限来进行，也可以使用一些基本的导数公式进行求解。

以下是一些常见导数公式：1. 常数函数 f(x) = C 的导数为 0，即 f'(x) = 0。

2. 幂函数 f(x) = x^n（n 为常数）的导数为 f'(x) = nx^(n-1)。

3. 指数函数 f(x) = e^x 的导数为 f'(x) = e^x。

4. 对数函数 f(x) = ln(x) 的导数为 f'(x) = 1/x。

5. 三角函数的导数：- 正弦函数的导数为 f'(x) = cos(x)。

- 余弦函数的导数为 f'(x) = -sin(x)。

- 正切函数的导数为 f'(x) = sec^2(x)。

...（其他三角函数的导数公式根据需要补充）四、导数与函数的像变化函数的导数与函数的像变化密切相关，导数可以帮助我们研究函数在不同区间的增减性、极值点、拐点等重要性质。

1. 增减性：若函数在某区间上的导数始终大于零，则函数在该区间上单调递增；若导数始终小于零，则函数在该区间上单调递减；若导数恒为零，则函数在该区间上为常数函数。

函数图像与导数是微积分中重要的概念。

图像是函数的可视化表示，而导数是函数与其自变量之间的关系。

理解函数图像与导数之间的关系对于解决实际问题和深入理解数学的本质具有重要意义。

首先，我们来了解一下函数图像。

函数图像是函数在坐标系中的几何表达。

它展示了函数的输出值随着自变量的变化而变化的规律。

通过观察函数图像，我们可以获得函数的性质、特点和行为。

例如，考虑一个简单的一次函数 y = 2x + 1。

我们可以通过将自变量 x 的值代入函数来计算出相应的 y 值，并绘制出这些点。

通过连接这些点，我们可以得到一条直线。

这就是函数 y = 2x + 1 的图像。

我们可以看到，随着 x 的增加，y 也以一定的比例增加，从而得到一条斜率为 2 的直线。

接下来，让我们转向导数的概念。

导数可以被认为是函数图像的变化率。

它衡量了函数在某个特定点上的斜率，描述了函数在该点的瞬时变化情况。

通过导数，我们可以深入了解函数的特性，并解决一些实际问题。

导数可以通过求取函数在某一点的斜率来计算。

对于函数 y = 2x + 1，我们可以通过求取不同点处的导数来了解它的变化率。

对于任意给定的 x0，我们计算出在该点上函数图像的切线斜率。

这个切线斜率就是导数。

对于一次函数 y = 2x + 1，求导后得到的导函数为y’ = 2。

这意味着在这个函数图像的任何一个点上，其变化率都为常数。

导函数为正数时，说明函数是递增的；导函数为负数时，说明函数是递减的。

进一步，我们可以解析地理解函数图像与导数的关系。

对于函数 y = 2x + 1，导函数y’ = 2 表示该函数的斜率为 2，在每个点上都是如此。

换句话说，这是一条直线，而且其斜率不会改变。

这个结论可以在函数图像上直观地看到，因为函数图像是一条直线。

在更复杂的函数中，导数表达了函数图像的曲线特性。

当导数为正时，函数图像呈现上升态势；当导数为负时，函数图像呈现下降态势。

此外，导数的变化量也提供了函数图像曲线的“弯曲”程度的信息。