(完整版)函数与导函数图像

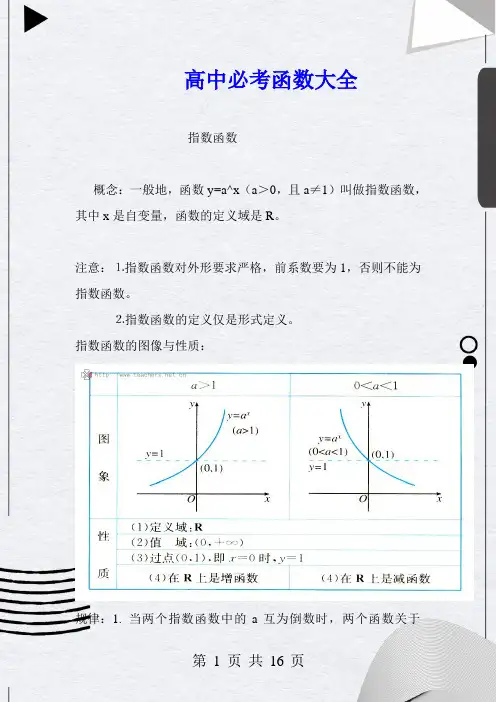
高中必考函数大全指数函数概念：一般地，函数y=a^x（a＞0，且a≠1）叫做指数函数，其中x是自变量，函数的定义域是R。

注意：⒈指数函数对外形要求严格，前系数要为1，否则不能为指数函数。

⒉指数函数的定义仅是形式定义。

指数函数的图像与性质：规律：1. 当两个指数函数中的a互为倒数时，两个函数关于y轴对称，但这两个函数都不具有奇偶性。

2.当a＞1时，底数越大，图像上升的越快，在y轴的右侧，图像越靠近y轴；当0＜a＜1时，底数越小，图像下降的越快，在y轴的左侧，图像越靠近y轴。

在y轴右边“底大图高”；在y轴左边“底大图低”。

3.四字口诀：“大增小减”。

即：当a＞1时，图像在R上是增函数；当0＜a＜1时，图像在R上是减函数。

4. 指数函数既不是奇函数也不是偶函数。

比较幂式大小的方法：1.当底数相同时，则利用指数函数的单调性进行比较；2.当底数中含有字母时要注意分类讨论；3.当底数不同，指数也不同时，则需要引入中间量进行比较；4.对多个数进行比较，可用0或1作为中间量进行比较底数的平移：在指数上加上一个数，图像会向左平移；减去一个数，图像会向右平移。

在f(X)后加上一个数，图像会向上平移；减去一个数，图像会向下平移。

对数函数1.对数函数的概念由于指数函数y=a x在定义域(-∞，+∞)上是单调函数，所以它存在反函数，我们把指数函数y=a x(a＞0，a≠1)的反函数称为对数函数，并记为y=log a x(a＞0，a≠1).因为指数函数y=a x的定义域为(-∞，+∞)，值域为(0，+∞)，所以对数函数y=log a x的定义域为(0，+∞)，值域为(-∞，+∞).2.对数函数的图像与性质对数函数与指数函数互为反函数，因此它们的图像对称于直线y=x. 据此即可以画出对数函数的图像，并推知它的性质.为了研究对数函数y=log a x(a＞0，a≠1)的性质，我们在同一直角坐标系中作出函数y=log 2x ，y=log 10x ，y=log 10x,y=log 21x,y=log 101x 的草图由草图，再结合指数函数的图像和性质，可以归纳、分析出对数函数y=log a x(a ＞0，a ≠1)的图像的特征和性质.见下表. 图 象 a ＞1a ＜1性 (1)x ＞0(2)当x=1时，y=0质(3)当x＞1时，y＞00＜x＜1时，y＜0 (3)当x＞1时，y＜0 0＜x＜1时，y＞0(4)在(0，+∞)上是增函数(4)在(0，+∞)上是减函数补充性质设y1=log a x y2=log b x其中a＞1，b＞1(或0＜a＜1 0＜b＜1)当x＞1时“底大图低”即若a＞b则y1＞y2当0＜x＜1时“底大图高”即若a＞b，则y1＞y2比较对数大小的常用方法有：(1)若底数为同一常数，则可由对数函数的单调性直接进行判断.(2)若底数为同一字母，则按对数函数的单调性对底数进行分类讨论.(3)若底数不同、真数相同，则可用换底公式化为同底再进行比较.(4)若底数、真数都不相同，则常借助1、0、-1等中间量进行比较.3.指数函数与对数函数对比名称指数函数对数函数一般形式y=a x(a＞0，a≠1) y=log a x(a＞0，a≠1)定义域(-∞，+∞) (0，+∞)值域(0，+∞) (-∞，+∞)函数值变化情况当a＞1时，⎪⎩⎪⎨⎧<<==>>)0(1)0(1)0(1xxxa x当0＜a＜1时，⎪⎩⎪⎨⎧<>==><)0(1)0(1)0(1xxxa x当a＞1时⎪⎩⎪⎨⎧<<==>>)1(0)1(0)1(0logxxxxa当0＜a＜1时，⎪⎩⎪⎨⎧<>==><)1(0)1(0)1(0logxxxxa单调性当a＞1时，a x是增函数；当0＜a＜1时，a x是减函数. 当a＞1时，log a x是增函数；当0＜a＜1时，log a x是减函数.图像y=a x的图像与y=log a x的图像关于直线y=x对称.幂函数幂函数的图像与性质幂函数ny x=随着n的不同，定义域、值域都会发生变化，可以采取按性质和图像分类记忆的方法．熟练掌握ny x=，当112,1,,,323n=±±±的图像和性质，列表如下．从中可以归纳出以下结论：①它们都过点()1,1，除原点外，任何幂函数图像与坐标轴都不相交，任何幂函数图像都不过第四象限．② 11,,1,2,332a =时，幂函数图像过原点且在[)0,+∞上是增函数．③ 1,1,22a =---时，幂函数图像不过原点且在()0,+∞上是减函数．④ 任何两个幂函数最多有三个公共点．n y x =奇函数偶函数非奇非偶函数1n >01n <<0n <定义域 R R R奇偶性奇奇奇非奇非奇OxyOxyOxyOxyOxyOx yOxyOxyOxy偶在第Ⅰ象限的增减性在第Ⅰ象限单调递增在第Ⅰ象限单调递增 在第Ⅰ象限单调递增 在第Ⅰ象限单调递增 在第Ⅰ象限单调递减幂函数y x α=（x ∈R ，α是常数）的图像在第一象限的分布规律是：①所有幂函数y x α=（x ∈R ，α是常数）的图像都过点)1,1(； ②当21,3,2,1=α时函数y x α=的图像都过原点)0,0(；③当1=α时，y x α=的的图像在第一象限是第一象限的平分线（如2c ）；④当3,2=α时，y x α=的的图像在第一象限是“凹型”曲线（如1c ）⑤当21=α时，y x α=的的图像在第一象限是“凸型”曲线（如3c ）⑥当1-=α时，y x α=的的图像不过原点)0,0(，且在第一象限是“下滑”曲线（如4c ）当0>α时，幂函数y x α=有下列性质： （1）图象都通过点)1,1(),0,0(；（2）在第一象限内都是增函数；（3）在第一象限内，1>α时，图象是向下凸的；10<<α时，图象是向上凸的；（4）在第一象限内，过点)1,1(后，图象向右上方无限伸展。

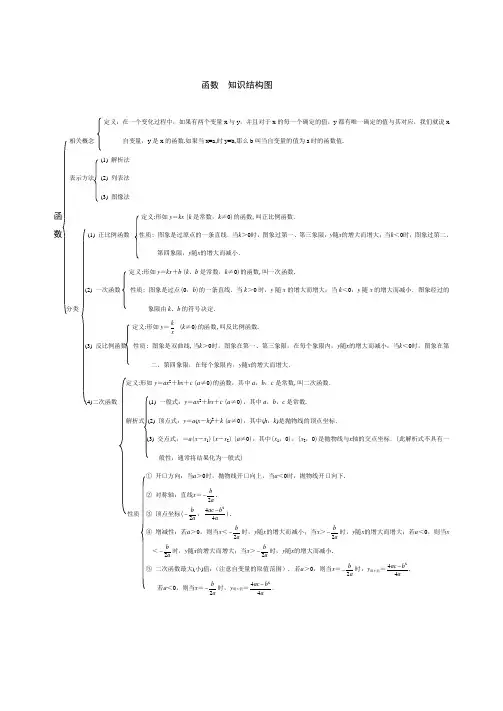
函数 知识结构图定义：在一个变化过程中，如果有两个变量x 与y ，并且对于x 的每一个确定的值，y 都有唯一确定的值与其对应，我们就说x相关概念 自变量，y 是x 的函数.如果当x=a,时y=b,那么b 叫当自变量的值为a 时的函数值.(1) 解析法表示方法 (2) 列表法(3) 图像法函 定义:形如y ＝kx (k 是常数，k ≠0)的函数,叫正比例函数．数 (1) 正比例函数 性质: 图象是过原点的一条直线．当k ＞0时，图象过第一、第三象限，y 随x 的增大而增大；当k ＜0时，图象过第二、第四象限，y 随x 的增大而减小．定义:形如y ＝kx ＋b (k 、b 是常数，k ≠0)的函数,叫一次函数.(2) 一次函数 性质: 图象是过点(0，b )的一条直线．当k ＞0时，y 随x 的增大而增大；当k ＜0，y 随x 的增大而减小．图象经过的分类 象限由k 、b 的符号决定．定义:形如y ＝k x(k ≠0)的函数,叫反比例函数. (3) 反比例函数 性质: 图象是双曲线,当k ＞0时，图象在第一、第三象限，在每个象限内，y 随x 的增大而减小；当k ＜0时，图象在第二、第四象限，在每个象限内，y 随x 的增大而增大．定义:形如y ＝ax 2＋bx ＋c (a ≠0)的函数，其中a ，b ，c 是常数,叫二次函数．(4)二次函数 (1) 一般式：y ＝ax 2＋bx ＋c (a ≠0)，其中a ，b ，c 是常数.解析式 (2) 顶点式：y ＝a (x －h )2＋k (a ≠0)，其中(h ，k )是抛物线的顶点坐标．(3) 交点式：＝a (x －x 1)(x －x 2) (a ≠0)，其中(x 1，0)，(x 2，0)是抛物线与x 轴的交点坐标．(此解析式不具有一般性，通常将结果化为一般式)① 开口方向：当a ＞0时，抛物线开口向上，当a ＜0时，抛物线开口向下.② 对称轴：直线x ＝2b a-. 性质 ③ 顶点坐标(2b a-，244ac b a -). ④ 增减性：若a ＞0，则当x ＜2b a -时，y 随x 的增大而减小；当x ＞2b a -时，y 随x 的增大而增大；若a ＜0，则当x ＜2b a -时，y 随x 的增大而增大；当x ＞2b a-时，y 随x 的增大而减小. ⑤ 二次函数最大(小)值：（注意自变量的取值范围）. 若a ＞0，则当x ＝2b a-时，y 最小值＝244ac b a -. 若a ＜0，则当x ＝2b a-时，y 最大值＝244ac b a -．。

函数图像是必考点，对于研究函数的单调性、奇偶性以及最值（值域）、零点有举足轻重的作用，但是很多同学看到眼花缭乱的函数解析式，就已经晕头转向了。

今天给大家整理了高中函数相关资料，希望能帮助高中生数学得高分！下面是基本初等函数的图像以及函数变换的规律，希望大家能学明白！一、基本初等函数的图像1.一次函数性质：一次函数图像是直线，当k>0时，函数单调递增；当k<0时，函数单调递减。

2.二次函数性质：二次函数图像是抛物线，a决定函数图像的开口方向，判别式b^2-4ac决定了函数图像与x轴的交点，对称轴两边函数的单调性不同。

3.反比例函数性质：反比例函数图像是双曲线，当k>0时，图像经过一、三象限；当k<0时，图像经过二、四象限。

要注意表述函数单调性时，不能说在定义域上单调，而应该说在（-∞，0），（0，∞）上单调。

4.指数函数当0<a<b<1<c<d时，指数函数的图像如下图：不同底的指数函数图像在同一个坐标系中时，一般可以做直线x=1，与各函数的交点，根据交点纵坐标的大小，即可比较底数的大小。

5.对数函数当底数不同时，对数函数的图像是这样变换的：6.幂函数y=x^a性质：先看第一象限，即x>0时，当a>1时，函数越增越快；当0<a<1时，函数越增越慢；当a<0时，函数单调递减；然后当x<0时，根据函数的定义域与奇偶性判断函数图像即可。

7.对勾函数对于函数y=x+k/x，当k>0时，才是对勾函数，可以利用均值定理找到函数的最值。

二、函数图像的变换注意：对于函数图像的变换，有的时候，看到解析式，可能会有两种以上的变换，尤其是针对x轴上的，那么此时，一定要根据上面的规则，判断好顺序，否则顺序错了，可能就没办法经过变换得到了！例如：画出函数y=ln|2-x|的图像通过研究这个函数解析式，我们知道此函数是由基本初等函数y=lnx 通过变换而来，那么这个函数经过了几步变换呢？变换的顺序又是如何？通过解析式x上附加的东西，我们会发现，会有对称变换，x前面加了负号，还有翻折变换，x上面还有绝对值，还有平移变换，前面加了一个2，既然有3种变换，那么顺序如何呢？牢记住一点：针对x 轴上的变换，那就一定要看x这个符号有啥变化。

常见函数性质汇总及简单评议对称变换常数函数 f (x ）=b (b ∈R) 1）、y=a 和 x=a 的图像和走势2）、图象及其性质：函数f (x ）的图象是平行于x 轴或与x 轴重合(垂直于y 轴）的直线一次函数 f (x )=kx +b (k ≠0，b ∈R ）1)、两种常用的一次函数形式:斜截式——点斜式——2）、对斜截式而言,k 、b 的正负在直角坐标系中对应的图像走势： 3）、|k ｜越大，图象越陡；|k|越小，图象越平缓 4）、定 义 域:R 值域:R单调性：当k 〉0时 ；当k<0时奇 偶 性：当b =0时，函数f （x )为奇函数;当b ≠0时,函数f (x ）没有奇偶性； 反 函 数:有反函数（特殊情况下：K=±1并且b=0的时候)。

补充：反函数定义：例题:定义在r y=f （x ）； y=g （x ）都有反函数,且f （x-1）和g —1(x ）函数的图像关于y=x 对称，若f （4）=周 期 性:无 5）、一次函数与其它函数之间的练习 1、常用解题方法：xy b Of (x )=bx yOf (x )=kx +b R 2）点关于直线（点）对称，求点的坐标2、与曲线函数的联合运用反比例函数 f (x ）=xk(k ≠0，k 值不相等永不相交；k 越大，离坐标轴越远） 图象及其性质:永不相交，渐趋平行;当k 〉0时，函数f (x ）的图象分别在第一、第三象限；当k<0时，函数f (x ）的图象分别在第二、第四象限； 双曲线型曲线，x 轴与y 轴分别是曲线的两条渐近线；既是中心对成图形也是轴对称图形定 义 域：),0()0,(+∞-∞ 值 域：),0()0,(+∞-∞ 单 调 性：当k> 0时；当k< 0时 周 期 性:无奇 偶 性：奇函数 反 函 数：原函数本身补充：1、反比例函数的性质2、与曲线函数的联合运用（常考查有无交点、交点围城图行的面积)—-入手点常有两个——⑴直接带入,利用二次函数判别式计算未知数的取值；⑵利用斜率，数形结合判断未知数取值（计算面积基本方法也基于此）3、反函数变形（如右图）1）、y=1/（x —2）和y=1/x —2的图像移动比较 2)、y=1/(—x)和y=—（1/x)图像移动比较3）、f （x ）= dcx bax ++ (c ≠0且 d ≠0）（补充一下分离常数）（对比标准反比例函数，总结各项内容)二次函数 一般式：)0()(2≠++=a c bx ax x f 顶点式:)0()()(2≠+-=a h k x a x f两根式：)0)()(()(21≠--=a x x x x a x f图象及其性质：①图形为抛物线，对称轴为 ，顶点坐标为 ②当0>a 时，开口向上，有最低点 当0<a 时。

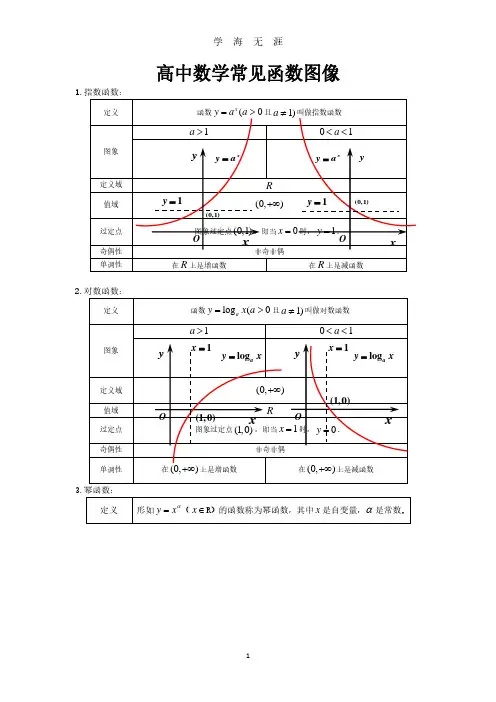
高中数学常见函数图像1.指数函数：定义函数(0x y a a =>且1)a ≠叫做指数函数图象1a >01a <<定义域 R值域(0,)+∞过定点 图象过定点(0,1)，即当0x=时，1y =．奇偶性 非奇非偶单调性在R 上是增函数在R 上是减函数2.对数函数：定义函数log (0a y x a =>且1)a ≠叫做对数函数图象1a >01a <<定义域 (0,)+∞值域 R过定点 图象过定点(1,0)，即当1x =时，0y =． 奇偶性 非奇非偶单调性在(0,)+∞上是增函数在(0,)+∞上是减函数3.幂函数：定义形如αx y =（x ∈R ）的函数称为幂函数，其中x 是自变量，α是常数.xa y =xy(0,1)O1y =xa y =xy (0,1)O1y =xyO(1,0)1x =log a y x=xyO(1,0)1x =log a y x=图像性质过定点：所有的幂函数在(0,)+∞都有定义，并且图象都通过点(1,1)． 单调性：如果0α>，则幂函数的图象过原点，并且在[0,)+∞上为增函数．如果0α<，则幂函数的图象在(0,)+∞上为减函数，在第一象限内，图象无限接近x 轴与y 轴．4.函数sin y x =cos y x = tan y x =图象定义域R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1−[]1,1−R最值 当22x k ππ=+()k ∈Z 时，max 1y =； 当22xk ππ=−当()2x k k π=∈Z 时，max 1y =；当2xk ππ=+既无最大值也无最小值()k ∈Z 时，min 1y =−．()k ∈Z 时，min 1y =−．周期性 2π2ππ奇偶性奇函数 偶函数奇函数单调性在2,222k k ππππ⎡⎤−+⎢⎥⎣⎦()k ∈Z 上是增函数；在32,222k k ππππ⎡⎤++⎢⎥⎣⎦()k ∈Z 上是减函数．在[]()2,2k k k πππ−∈Z 上是增函数；在[]2,2k k πππ+()k ∈Z 上是减函数．在,22k k ππππ⎛⎫−+⎪⎝⎭()k ∈Z 上是增函数．对称性对称中心()(),0k k π∈Z对称轴()2x k k ππ=+∈Z对称中心(),02k k ππ⎛⎫+∈Z⎪⎝⎭ 对称轴()x k k π=∈Z对称中心(),02k k π⎛⎫∈Z ⎪⎝⎭无对称轴。

五大基本函数图像及性质经过数学发展的几千年，函数成为数学研究的主要内容之一，用来描述理解宇宙规律的精妙抽象工具，而函数图像则是这些函数形式反射出来的表达形式。

在数学探索中，五种基本函数图像最为常见，它们分别是：直线函数图像，二次函数图像，指数函数图像，对数函数图像和正弦函数图像。

直线函数图像是函数图像中最简单的一种形式，它可以用方程的形式y=kx +b来表示，其中K表示斜率，b表示偏移量，x、y是函数的模型变量，模型变量是可以表达数学物理实验结果的变量。

斜率便是表示函数图像斜线斜率，偏移量是表示函数图像经过y轴的截距，而此类函数一般没有极限，但伴随着变量不断变化而无限的延伸。

这种特性使它成为很多具有统计推论意义的实验结果的基础数据，在解决微积分问题时也是非常重要的概念。

二次函数图像的基本形式为y=ax^2 +bx +c，其中a,b,c代表的是函数的方程的三个常数，x是函数模型变量，y是函数的值，在实际应用中，一般需要将该方程写成y=a(x-h)^2 +k的形式；a为非负实数，当a为0时，表示函数直线，当a不为0时，表示函数曲线；h是函数的极值点横坐标，k是函数极值点的点的纵坐标，这样的函数有两个极值点，极值点的大小取决于a的正负，正值表示极值点为最小值，负值表示极值点为最大值。

指数函数图像是根据指数函数进行描述的，其基本形式为y=a^x，其中a为正实数，x为函数模型变量，y为函数值，这种函数图像有两个极限，即横坐标上趋于无穷大时，纵坐标为正负无穷大，指数函数在应用时非常广泛，它可以用来描述多种不同的物理实验结果，比如温度变化，加速速度的变化等等。

对数函数图像是根据对数函数来描绘的，其基本形式为y=loga(x)，其中a是底数，x是函数模型变量，y是函数值，这种函数图像的横坐标上的极限为0，纵坐标上的极限为正负无穷大，对数函数可以用来描述指数函数和二次函数的变化，在温度变化，分子运动速度和其它变化等等应用也十分重要。

经典数学函数图像(大全)1. 一次函数图像一次函数图像是一条直线，其一般形式为 y = mx + b，其中 m是斜率，b 是 y 轴截距。

当 m > 0 时，直线向上倾斜；当 m < 0 时，直线向下倾斜。

2. 二次函数图像二次函数图像是一个抛物线，其一般形式为 y = ax^2 + bx + c，其中 a、b、c 是常数。

当 a > 0 时，抛物线开口向上；当 a < 0 时，抛物线开口向下。

3. 三角函数图像三角函数图像包括正弦函数、余弦函数和正切函数。

正弦函数图像是一条波动曲线，余弦函数图像与正弦函数图像相似，但相位差为π/2。

正切函数图像是一条周期性振荡的曲线。

4. 指数函数图像指数函数图像是一条上升或下降的曲线，其一般形式为 y = a^x，其中 a 是底数，x 是指数。

当 a > 1 时，曲线上升；当 0 < a < 1 时，曲线下降。

5. 对数函数图像对数函数图像是一条上升或下降的曲线，其一般形式为 y =log_a(x)，其中 a 是底数，x 是真数。

当 a > 1 时，曲线上升；当0 < a < 1 时，曲线下降。

6. 双曲函数图像双曲函数图像包括双曲正弦函数、双曲余弦函数和双曲正切函数。

双曲正弦函数和双曲余弦函数图像都是上升或下降的曲线，而双曲正切函数图像是一条周期性振荡的曲线。

7. 幂函数图像幂函数图像是一条上升或下降的曲线，其一般形式为 y = x^n，其中 n 是指数。

当 n > 0 时，曲线上升；当 n < 0 时，曲线下降。

8. 反比例函数图像反比例函数图像是一条双曲线，其一般形式为 y = k/x，其中 k是常数。

当 k > 0 时，曲线位于第一和第三象限；当 k < 0 时，曲线位于第二和第四象限。

经典数学函数图像(大全)3. 反三角函数图像反三角函数是三角函数的反函数，包括反正弦函数、反余弦函数和反正切函数。

高三数学知识点导数图表导数是高中数学中非常重要的一个概念，它是微积分的核心内容之一。

导数图表是学习和理解导数概念的重要工具，通过图表我们可以清晰地看到函数在不同点上的变化趋势以及导数的特性。

本文将介绍高三数学中一些常见的导数知识点，并用图表形式展示。

一、导数的定义导数表示函数在某一点上的变化速率，可用以下定义来表达：若函数f(x)在点x0处可导，则其导数为f'(x0) = lim(x->x0)[f(x)-f(x0)] / (x-x0)。

二、导数的基本性质1. 常数函数的导数为0：若f(x) = c，其中c为常数，则f'(x) = 0。

2. 幂函数的导数：若f(x) = x^n，其中n为整数，则f'(x) = nx^(n-1)。

3. 指数函数的导数：若f(x) = a^x，其中a为正实数且a≠1，则f'(x) = ln(a) * a^x。

4. 对数函数的导数：若f(x) = loga(x)，其中a为正实数且a≠1，则f'(x) = 1 / (x *ln(a))。

5. 三角函数的导数：若f(x) = sin(x)，则f'(x) = cos(x)；若f(x) = cos(x)，则f'(x) = -sin(x)；若f(x) = tan(x)，则f'(x) = sec^2(x)。

三、导数的几何意义导数的几何意义是函数曲线上某一点处的切线的斜率。

假设函数f(x)在点(x0, f(x0))处可导，则切线的斜率等于导数f'(x0)。

通过导数的几何意义，我们可以直观地理解函数在不同点上的变化趋势。

四、导数图表示例下面给出几个常见函数在不同点上的导数图表示例：1. 幂函数 f(x) = x^n导数图表：```x f(x) = x^2 f'(x) = 2x-3 9 -6-2 4 -4-1 1 -20 0 01 1 22 4 43 9 6```2. 指数函数 f(x) = a^x（a > 1）导数图表：```x f(x) = 2^x f'(x) = ln(2) * 2^x -3 1/8 -ln(2)/4-2 1/4 -ln(2)/2-1 1/2 -ln(2)0 1 ln(2)1 2 ln(2) * 22 4 ln(2) * 43 8 ln(2) * 8```3. 三角函数 f(x) = sin(x)导数图表：```x f(x) = sin(x) f'(x) = cos(x)-3.14 0 1-1.57 -1 00 0 11.57 1 03.14 0 -1```通过以上导数图表的示例，我们可以看到函数在不同点上的导数值及其变化趋势。

基本初等函数的导数表1. y=c y'=02. y=αμy'=μα(μ-1)3. y=a x y'=a x lnay=e x y'=e x4. y=loga x y'=loga e/xy=lnx y'=1/x5. y=sinx y'=cosx6. y=cosx y'=-sinx7. y=tanx y'=(secx)2=1/(cosx)28. y=cotx y'=-(cscx)2=-1/(sinx)29. y=arc sinx y'=1/√(1-x^2)10.y=arc cosx y'=-1/√(1-x^2)11.y=arc tanx y'=1/(1+x^2)12.y=arc cotx y'=-1/(1+x^2)13.y=sh x y'=ch x14.y=ch x y'=sh x15.y=thx y'=1/(chx)^216.y=ar shx y'=1/√(1+x^2)17.y=ar chx y'=1/√(x^2-1)18.y=ar th y'=1/(1-x^2)1、求一次函数y=ax+b的导数。

导数其实就是函数图象在某一点的斜率,对于一次函数来说,各点斜率都是相同的,加的那个b对斜率没有影响,可忽略,剩下y=ax,a就是函数的斜率,也就是导数。

可设任意两点(x1,y1)(x2,y2),斜率= (y2-y1) /(x2-x1)=a(1)当a=0,且b=0时,y=0 y'。

(2)当a=0,b不等于0时,y=b y'=0(3)当a不等于0,y'=a2、求二次函数y=ax2+bx+c的导数f(x)'=2ax+b3、求y=x3+ax2-4/3 a的导数y′=3x2+2ax.例:y=ax3+ax2+4x求单调区间,用导数的方法求y'=3ax2+2ax+43ax2+2ax+4=03a(x+1/3)2=a/3 -4a>=12时-1/3-√(1/9-4/3a) <x<-1/3+√(1/9-4/3a) f'(x)<0 递减x<-1/3-√(1/9-4/3a) 或x>-1/3+√(1/9-4/3a),f'(x)>0 递增a<12时,y'>0 单调递增例:用导数求函数y=-x3-2x2-4x+5的单调区间y'=-3x2-4x-4判别式小于0,开口向下所以y'<0所以减区间是R例:若函数f(x)的导数f'(x)=x^2-4x+3,则函数f(x+1)的单调递减区间为解:由f'(x)<0得,x^2-4x+3<0,解得1<x<3,即f(x)的单调递减区间为(1,3),f(x+1)的图像是由f(x)的图像向左移动一个单位得到的,所以f(x+1)的单调递减区间为(1-1,3-1),即(0, 2),所以f(x+1)的单调递减区间是(0,2)。

Sin的导函数图像为理解正弦波，我们必须学习Sin、Cos、Tan函数的曲线图像。

假设我们有一个圆，并设有一个角为，角夹在x轴和单位圆的半径之间，半径与单位圆交点处的坐标为（x,y）。

我们对三角函数做了新的定义：现在我们试着画出他们的曲线，那么我们先开始对Sin 画出曲线，我们先绘制一个表格：当为零弧度时，Sin会是多少？我们画出图来直观看：红色就是那条0弧度的半径，那个交点是单位圆的交点，这点坐标是（1，0）。

所以，当它与单位圆的交点是坐标（1，0），那么Sin 就等于坐标y，即为0。

当为π/2弧度时，Sin会是多少？我们画出图来直观看：橙色就是那条π/2弧度的半径，那个交点是单位圆的交点，这点坐标是（0，1）。

所以，当它与单位圆的交点是坐标（0，1），那么Sin 就等于坐标y，即为1。

当为π弧度时，Sin会是多少？我们画出图来直观看：绿色就是那条3π/2弧度的半径，那个交点是单位圆的交点，这点坐标是（-1，0）。

所以，当它与单位圆的交点是坐标（-1，0），那么Sin 就等于坐标y，即为0。

当为3π/2弧度时，Sin会是多少？我们画出图来直观看：紫色就是那条3π/2弧度的半径，那个交点是单位圆的交点，这点坐标是（0，-1）。

所以，当它与单位圆的交点是坐标（0，-1），那么Sin 就等于坐标y，即为-1。

当为2π弧度时，Sin会是多少？我们画出图来直观看：红色就是那条2π弧度的半径，那个交点是单位圆的交点，这点坐标是（1，0）。

所以，当它与单位圆的交点是坐标（1，0），那么Sin 就等于坐标y，即为0。

这样我们得到了：现在我们开始尝试把这些点连接起来，从而得到 sin 函数的图像：这就是正弦曲线，它像是震荡，或者上下移动。

Cos函数和Tan函数，可以尝试自己画一下。