[]相似三角形判定三边两边夹角

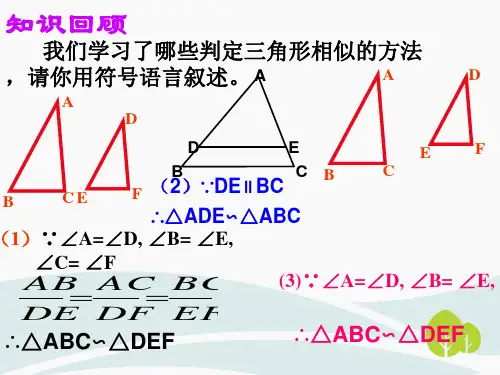
三角形相似的判定方法一1、定义法：三个对应角相等，三条对应边成比例的两个三角形相似．2、平行法：平行于三角形一边的直线和其它两边(或两边的延长线)相交，所构成的三角形与原三角形相似．3、判定定理1：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．简述为：两角对应相等，两三角形相似．4、判定定理2：如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似．简述为：两边对应成比例且夹角相等，两三角形相似． 5、判定定理3：如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这 两个三角形相似．简述为：三边对应成比例，两三角形相似． 特殊、判定直角三角形相似的方法：(1)以上各种判定均适用．(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．(3)直角三角形被斜边上的高分成的两个直角三角形与原三角形相似． 注：射影定理：在直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项。

每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。

如图，Rt △ABC 中，∠BAC=90°，AD 是斜边BC 上的高， 则AD 2=BD ·DC ，AB 2=BD ·BC ，AC 2=CD ·BC 。

二 相似三角形常见的图形三、1，下面我们来看一看相似三角形的几种基本图形：（1） 如图：称为“平行线型”的相似三角形（有“A 型”与“X 型”图）(2) 如图：其中∠1=∠2，则△ADE ∽△ABC 称为“斜交型”的相似三角形。

（有“反A 共角型”、“反A 共角共边型”、 “蝶型”）ACD E 12AADDEE12412DBCEAD(3)BCAE (2)CB（3） 如图：称为“垂直型”（有“双垂直共角型”、“双垂直共角共边型（也称“射影定理型”）”“三垂直型”）(4)如图：∠1=∠2，∠B=∠D ，则△ADE ∽△ABC ，称为“旋转型”的相似三角形。

初三数学---相似三角形和解直角三角形一、相似三角形1．相似三角形判定定理：（1）平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似. （2）判定定理1如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．即“两角对应相等，两三角形相似”．（3）判定定理2如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似．即“两边对应成比例且夹角相等，两三角形相似”．（4）判定定理3如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似．即“三边对应成比例，两三角形相似”．（5）若△1∽△2、△2∽△3、则△1∽△3．对于直角三角形相似，还有如下判定定理：（6）如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．（7）直角三角形被斜边上的高分成的两个直角三角形和原三角形相似．2．相似三角形的性质（1）相似三角形的对应角相等；（2）相似三角形的对应边成比例；（3）相似三角形的对应高的比、对应中线的比与对应角平分线的比都等于相似比；（4）相似三角形周长比等于相似比；（5）相似三角形面积的比等于相似比的平方．二、锐角三角函数1．掌握锐角三角函数的定义，准确地进行计算．2．互余角的三角函数间的关系（1）sin（90°－）＝cos；（2）cos（90°－）＝sin；（3）．3．同角三角函数间的关系（1）；（2）．三、解直角三角形1．如图，在Rt△ABC中，∠C＝90°，（1）三边之间的关系：a2＋b2＝c2；（2）两锐角之间的关系：∠A＋∠B＝90°；（3）边与角之间的关系：，，．2．如图，若直角三角形ABC中，CD⊥AB于点D，设CD＝h，AD＝q，DB＝p，则由△CBD∽△ABC，得a2＝pc；由△CAD∽△BAC，得b2＝qc；由△ACD∽△CBD，得h2＝pq；由△ACD∽△ABC或由△ABC的面积，得ab＝ch．从三角函数的角度考虑，有由，得a2＝pc；同理，得b2＝qc；由，得h2＝pq；由，得ab＝ch．在有关直角三角形的相似问题中，可以尝试运用三角函数的知识来解题，即“三角法”．3．如图1，若CD是直角三角形ABC中斜边上的中线，则（1）CD＝AD＝BD＝；（2）点D是Rt△ABC的外心，外接圆半径．4．如图2，若r是直角三角形ABC的内切圆半径，则．图1 图2 图3 5．直角三角形的面积：（1）如图2，S△ABC．（2）如图3，S△ABC．6B＝90°－A，，，由求角A，B＝90°－A，由求角A，B＝90°－A例题分析例1．如图，等腰梯形ABCD中，AD∥BC，AD＝3，BC＝7，∠B＝60°，P为下底BC上一点（不与B，C重合），连接AP，过P点作PE交DC于E，使得∠APE＝∠B．（1）你认为图中哪两个三角形相似，为什么?（2）当点P在底边BC上自点B向C移动的过程中，是否存在一点P，使得DE∶EC＝5∶3?如果存在，求BP的长；如果不存在，请说明理由．例2．如图，正方形ABCD的边长为4，M，N分别是BC，CD上的两个动点，当M点在BC上运动时，保持AM和MN垂直．（1）求证：Rt△ABM∽Rt△MCN；（2）设BM＝x，梯形ABCN的面积为y，求y与x之间的函数关系式；当M点运动到什么位置时，四边形ABCN的面积最大，并求出最大面积；（3）当M点运动到什么位置时，Rt△ABM∽Rt△AMN，并求x的值．例3．如图，在△ABC中，∠BAC＝120°，AB＝10，AC＝5，求sin B·sin C的值．例4．如图，D是AB上一点，且CD⊥AC于C，S△ACD∶S△CDB＝2∶3，，AC＋CD＝18，求tan A的值和AB的长．5．如图，△OAB是边长为2的等边三角形，过点A的直线y＝与x轴交于点E．求点E的坐标．6．已知：如图（a），梯形ABCD中，AB∥CD，∠C＝90°，AB＝BC＝4，CD＝6．（1）E为BC边上一点，EF∥AD，交CD边于点F，FG∥EA，交AD边于点G，若四边形AEFG为矩形，求BE的长；（2）如图（b），将（1）中的∠AEF绕E点逆时针旋转为∠A′EF′，EF′交CD边于F′点，且F′点与D点不重合，射线EA′交AB边于点M，作F′N∥EA′交AD边于点N，设BM为x，△NF′D中，F′D边上的高为y，求y关于x的函数解析式及自变量x的取值范围．图（a）图（b）答案例1、解：（1）△ABP∽△PCE．其理由是除∠B＝∠C外，由于∠APE＝∠B＝60°，∠APC＝∠B＋∠BAP＝∠APE＋∠CPE，∴∠BAP＝∠CPE．由“两角对应相等，两三角形相似”可得△ABP∽△PCE．说明：此图形结构可以称为“一线三等角问题”．（2）作DF⊥BC于F，由已知可得CF＝，腰长AB＝CD＝2CF＝4，这样原问题转化为在底边BC上是否存在一点P，使得CE＝1.5．假设存在P点，使CE＝1.5，由△ABP∽△PCE，得，可得BP·PC＝AB·CE＝6．设BP＝x，∵BC＝BP＋PC＝7，∴PC＝7－x．∴x（7－x）＝6，即x2－7x＋6＝0．解得x1＝1，x2＝6．答：当BP＝1或BP＝6时，使得DE∶EC＝5∶3．例2、解：（1）在正方形ABCD中，AB＝BC＝CD＝4，∠B＝∠C＝90°．∵AM⊥MN，∴∠AMN＝90°．∴∠CMN＋∠AMB＝90°．在Rt△ABM中，∠MAB＋∠AMB＝90°，∴∠MAB＝∠CMN．∴Rt△ABM∽Rt△MCN．（2）∵Rt△ABM∽Rt△MCN，，即．．．当x＝2时，y取最大值，最大值为10．（3）∵∠B＝∠AMN＝90°，∴要使△ABM ∽△AMN，只需．由（1）知．∴BM＝MC．∴当点M运动到BC的中点时，△ABM∽△AMN，此时x＝2．例3、分析:为求sin B，sin C，需将∠B，∠C分别置于直角三角形之中，另外已知∠A的邻补角是60°，若要使其充分发挥作用，也需要将其置于直角三角形中，所以应分别过点B，C，向CA，BA的延长线作垂线段，即可顺利求解．解：过点B作BD⊥CA的延长线于点D，过点C作CE⊥BA的延长线于点E．∵∠BAC＝120°，∴∠BAD＝60°．；．又∵CD＝CA＋AD＝10，，．同理，可求得．．说明：由于锐角的三角函数是在直角三角形中定义的，因此若要求某个角的三角函数值，一般可以通过作垂线段等方法将其置于直角三角形中．例4、解：作DE∥AC交CB于E，则∠EDC＝∠ACD＝90°．∵，设CD＝4k（k＞0），则CE＝5k，由勾股定理得DE＝3k．∵△ACD和△CDB在AB边上的高相同，∴AD∶DB＝S△ACD∶S△CDB＝2∶3．．即．．∵AC＋CD＝18，∴5k＋4k＝18．解得k＝2．．．说明：本章解题的基本思路是将问题转化为解直角三角形的问题，转化的目标主要有两个，一是构造可解的直角三角形；二是利用已知条件通过设参数列方程．在解直角三角形时，常用的等量关系是：勾股定理、三角函数关系式、相等的线段、面积关系等．例5、解：作AF⊥x轴于F．∴OF＝OA·cos60°＝1，AF＝OF·．∴点A坐标为（1，）．代入直线解析式，得．．．当y＝0即时，x＝4．∴点E坐标为（4，0）．例6、解：（1）作AH⊥CD于点H（如图（c））可得∠1＝∠2＝∠D．由AB＝BC＝CH＝4可得HD＝CD－CH＝2．．．∴BE＝2，即E为BC的中点．（2）图（d），作NP⊥CD于点P，则PN＝y．可得∠4＝∠5＝∠6，它们的正切值相等．，即．，．，，∵CD＝CF′＋PF′＋PD，，即．整理，得．若点F′与点D重合（见图（e）），则∠BEM＝∠EDC，．．．∴x的取值范围为。

三角形相似的判定方法三角形相似的判定方法一1、定义法：三个对应角相等，三条对应边成比例的两个三角形相似．2、平行法：平行于三角形一边的直线和其它两边(或两边的延长线)相交，所构成的三角形与原三角形相似．3、判定定理1：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．简述为：两角对应相等，两三角形相似．4、判定定理2：如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似．简述为：两边对应成比例且夹角相等，两三角形相似． 5、判定定理3：如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似．简述为：三边对应成比例，两三角形相似．特殊、判定直角三角形相似的方法：(1)以上各种判定均适用．(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．(3)直角三角形被斜边上的高分成的两个直角三角形与原三角形相似．注：射影定理：在直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项。

每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。

如图，Rt△ABC中，∠BAC=90°，AD是斜边BC上的高，则AD=BD·DC，AB=BD·BC ，AC=CD·BC 。

22二相似三角形常见的图形三、1，下面我们来看一看相似三角形的几种基本图形：BC（1）如图：称为“平行线型”的相似三角形（有“A型”与“X型”图）(2)B(3)(2) 如图：其中∠1=∠2，则△ADE∽△ABC称为“斜交型”的相似三角形。

（有“反A共A角型”、“反A共角共边型”、“蝶型”）A4DCDEADE1E（3）如图：称为“垂直型”（有“双垂直共角型”、“双垂直共角共边型（也称“射影定理型”）”DEB(D)B(4)如图：∠1=∠2，∠B=∠D，则△ADE∽△ABC，称为“旋转型”的相似三角形。

三角形相似的判定方法6种相似三角形是初中数学中的一个非常重要的知识点，它也是历年中考的热点内容，通常考查以下三个部分：一是考查相似三角形的判定；二是考查利用相似三角形的性质解题；三是考查与相似三角形有关的综合内容。

以上试题的考查既能体现开放探究性，又能注重知识之间的综合性。

首先我们帮助学生突破相似三角形判定这个难点。

三角形相似的定义：对应角相等，对应边成比例的两个三角形叫做相似三角形比值与比的概念比值是一个具体的数字如：AB/EF=2而比不是一个具体的数字如：AB/EF=2：1判定方法证两个相似三角形应该把表示对应顶点的`字母写在对应的位置上。

如果是文字语言的“△ABC与△DEF相似”，那么就说明这两个三角形的对应顶点可能没有写在对应的位置上，而如果是符号语言的“△ABC∽△DEF”，那么就说明这两个三角形的对应顶点写在了对应的位置上。

知道了定义那么我们接下来就看看，三角形相似的判定的6种方法。

方法一(预备定理)平行于三角形一边的直线截其它两边所在的直线，截得的三角形与原三角形相似。

(这是相似三角形判定的定理，是以下判定方法证明的基础。

这个引理的证明方法需要平行线与线段成比例的证明)方法二如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。

方法三如果两个三角形的两组对应边成比例，并且相应的夹角相等,那么这两个三角形相似方法四如果两个三角形的三组对应边成比例，那么这两个三角形相似方法五(定义)对应角相等，对应边成比例的两个三角形叫做相似三角形三个基本型Z型A型反A型方法六两个直角三角形中，斜边与直角边对应成比例，那么两三角形相似。

一定相似的三角形1、两个全等的三角形(全等三角形是特殊的相似三角形，相似比为1：1)2、两个等腰三角形(两个等腰三角形，如果其中的任意一个顶角或底角相等，那么这两个等腰三角形相似。

)3、两个等边三角形(两个等边三角形，三角都是60度，且边边相等，所以相似)4、直角三角形中由斜边的高形成的三个三角形(母子三角形)。

三角形的相似三角形是几何学中的基本形状之一，它由三条边和三个角组成。

当两个三角形的对应角度相等且对应边的比例相等时，我们称这两个三角形为相似三角形。

本文将介绍三角形的相似性质、判定方法以及一些与相似三角形相关的常见应用。

一、三角形的相似性质相似三角形有以下几个重要的性质：1. AAA相似性质：如果两个三角形的三个内角分别相等，则这两个三角形相似。

2. AA相似性质：如果两个三角形的两个对应角分别相等，则这两个三角形相似。

3. SAS相似性质：如果两个三角形的两边对应成比例，并且它们的夹角相等，则这两个三角形相似。

4. SSS相似性质：如果两个三角形的三边对应成比例，则这两个三角形相似。

二、判定两个三角形是否相似的方法根据以上相似性质，我们可以采用以下方法判定两个三角形是否相似：1. 角-角-角（AAA）判定法：当两个三角形的三个内角分别相等时，可以判定这两个三角形相似。

2. 角-边-角（AA）判定法：当两个三角形的两个对应角分别相等，且其夹角处的边也成比例时，可以判定这两个三角形相似。

3. 边-角-边（SAS）判定法：当两个三角形的两边对应成比例，并且它们的夹角相等时，可以判定这两个三角形相似。

4. 边-边-边（SSS）判定法：当两个三角形的三边对应成比例时，可以判定这两个三角形相似。

三、相似三角形的常见应用相似三角形的性质可以应用于实际生活和解决几何问题中，下面介绍三个常见的应用场景：1. 测量高度：当无法直接测量高度时，可以利用相似三角形的性质通过测量已知长度和角度，并找到对应的相似三角形，从而计算出高度。

2. 影子问题：在阴影问题中，利用相似三角形的性质可以求解未知物体的尺寸。

通过测量物体和其阴影的长度，以及测量太阳光和物体的夹角，可以建立相似三角形的比例关系，从而计算出未知物体的尺寸。

3. 图像放大缩小：利用相似三角形的性质，可以通过控制不同比例的相似变换对图像进行放大或缩小。

这在摄影、计算机图形学等领域中广泛应用。

《相似三角形的判定——三边法、两边及其夹角法》的教学反思
《相似三角形的判定——三边法、两边及其夹角法》是九年制义务教育新课程标准九年级第二十七章的内容。

首先复习回顾使用定义和平行法两种方法判定三角形相似，为学习新知储备常见的A型X型两种相似三角形，教师抛出类比三角形全等的五种方法区判断两个三角形相似的猜想。

教师引导学生任意画一个三角形，再画一个三角形，使它的各边长都是原来三角形的各边长的k倍，画完后同桌交换你们的图形，分别度量这两个三角形的对应角，确定它们相等与否以及两个三角形相似与否。

充分探究后，师生共同推理验证：三边成比例的两个三角形相似，并且确定其几何语言。

为确保学生掌握该判定定理，学生做跟踪训练巩固新知。

巩固练习环节，教师提前预设，从添加第三边的角度入手满足三边成比例，推导两三角形相似。

遗憾的是，有些题目未指明对应边，故可能产生多种情况，有学生会想不全面。