M-K突变检验

% M-K 趋势检定clear, close all,clc % clear:清变数 close all:清图面 clc:清画面% define and assign the full file path using "file open" dialog[filename filepath]=uigetfile('data1.xls');full_filepath=[filepath filename];[X,TXTX,RAWX]=xlsread(full_filepath,1); % 数据全部读入,数据缺失不影响结果x=X(:,1); % x 时间 <nx1>y=X(:,2); % y 数据 <nx1>% 计算 Sn=size(y,1); % 数据个数S=0;for i=1:n-1S = S + sum(sign(y(i+1:n) - y(i))); % S 计算式end% 计算 VarSVarS=n*(n-1)*(2*n+5)/18;%计算 Zif S>0Z=(S-1)/sqrt(VarS);elseZ=(S+1)/sqrt(VarS);end% 计算 Zabsalpha1=0.05; % 信度 95% 的显著水平alpha2=0.01; % 信度 99% 的显著水平PZ1=norminv(1-alpha1/2,0,1);PZ2=norminv(1-alpha2/2,0,1);H=0; % 虚无假设Zabs=abs(Z);if Zabs >= PZ1H=1;elseH=0;endP_value=2*(1-normcdf(abs(Z),0,1)); % 若 P_value 比 alpha1 小,则否定虚无假设% 计算倾斜度ndash=n*(n -1)/2; % 对称矩阵上半部slope1= zeros( ndash, 1 ); % 起始归零m=0;for k = 1:n-1,for j = k+1:n,m=m+1;slope1(m) = ( y(j) - y(k) ) / (x(j) - x(k) ) ;% 分母非 (j-k) end;end;slope= median( slope1 ); % 中位数% 历线绘图yd=max(y)-min(y);figureplot(x,y,'b-o','linewidth',1.5);axis([min(x),max(x),min(y)-0.2*yd,max(y)+0.2*yd]); % 全距外扩 20% xlabel('时间','FontName','TimesNewRoman','FontSize',12);ylabel('数据','FontName','TimesNewRoman','Fontsize',12);title('数据历线图') %添加标题grid onoutput='数据历线图';saveas(gcf, output, 'jpg')% M-K 突变检定Sk=zeros(size(y)); % 起始归零UFk=zeros(size(y)); % 起始归零s1=0;for i=2:nfor j=1:iif y(i)>y(j)s1=s1+1;elses1=s1+0;end;end;Sk(i)=s1;E=i*(i-1)/4; % 均值Var=i*(i-1)*(2*i+5)/72; % 方差UFk(i)=(Sk(i)-E)/sqrt(Var);end;% 起始归零y2=zeros(size(y));Sk2=zeros(size(y));UBk=zeros(size(y));s2=0;for i=1:ny2(i)=y(n-i+1); % 逆序end;for i=2:nfor j=1:iif y2(i)>y2(j)s2=s2+1;elses2=s2+0;end;end;Sk2(i)=s2;E=i*(i-1)/4; % Sk2(i)的均值Var=i*(i-1)*(2*i+5)/72; % Sk2(i)的方差UBk(i)=-(Sk2(i)-E)/sqrt(Var);end;UBk2=zeros(size(y));for i=1:nUBk2(i)=UBk(n-i+1); % 逆序end;% 线性回归x1=x-x(1)+1; % x1 可为非连续时间序列,有缺失数据无所谓 x1< nx1 >,非 x1=[1:n]' r=corrcoef(x1,y) % 相关系数R2=r(1,2)^2C=polyfit(x1,y,1) % C(1):一次项系数 C(2):常数项系数% 画 UFk,UBk M-K统计量曲线图dFB=max(max(UFk)-min(UFk),max(UBk2)-min(UBk2));dFB1=min(min(UFk),min(UBk2))-0.2*dFB; % 全距外扩 20%dFB2=max(max(UFk),max(UBk2))+0.2*dFB;if dFB1>-PZ2dFB1=-5;endif dFB2<PZ2dFB2=5;endfigureplot(x,UFk,'r-','linewidth',1.5);hold onplot(x,UBk2,'b-','linewidth',1.5);plot(x ,PZ1*ones(n,1),'k-','linewidth',2);plot(x ,PZ2*ones(n,1),'g-','linewidth',2);axis([min(x),max(x),dFB1,dFB2]);legend('UF统计量','UB统计量','0.05显著水平','0.01显著水平'); xlabel('时间','FontName','TimesNewRoman','FontSize',12);ylabel('UFk UBk 统计量','FontName','TimesNewRoman','Fontsize',12); title('M-K 统计量曲线图') % 添加标题plot(x,0*ones(n,1),'k-.','linewidth',2) ;plot(x,-PZ1*ones(n,1),'k-','linewidth',2);plot(x,-PZ2*ones(n,1),'g-','linewidth',2);grid on % 画出主格网hold offoutput='M-K 统计量曲线图';saveas(gcf, output, 'jpg')[filename filepath]=uigetfile('test.xls');full_filepath=[filepath filename];xlswrite(full_filepath,x,'Sheet1','A1');xlswrite(full_filepath,UFk,'Sheet1','B1');xlswrite(full_filepath,UBk2,'Sheet1','C1');。

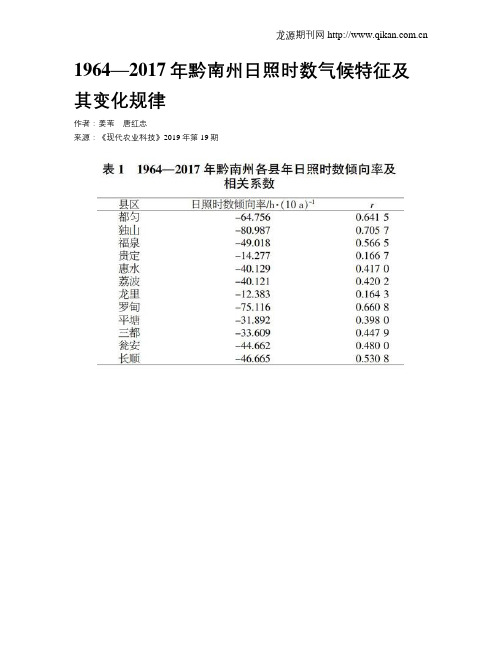
1964—2017年黔南州日照时数气候特征及其变化规律作者：姜苇唐红忠来源：《现代农业科技》2019年第19期摘要 ; ;本文采用线性趋势、滑动平均、Mann-Kendall等方法对贵州省黔南州12个站1964—2017年的年日照时数、季日照时数进行了线性趋势和突变特征分析。

结果表明，全州12个县年日照时数均呈减少趋势，其中独山和罗甸减少趋势最显著，分别为-80.398 7/10 a和-75.116/10 a;在突变检验中，仅荔波、惠水年平均日照时数存在突变现象，突变时间分别为1982年和1989年，但其他县仍存在明显的下降趋势。

另外，从空间分布来看，黔南州54年平均日照时数分布呈现西部、南部高，东部、北部低的特点，年平均值为700～1 800 h;最高值（≥1 800 h）区域出现在罗甸，最低值（≤700 h）区域出现在贵定和都匀市的部分地区。

关键词 ; ;日照时数;气候特征;变化规律;贵州黔南;1964—2017年中图分类号 ; ;P467 ; ; ; ;文献标识码 ; ;A文章编号 ; 1007-5739（2019）19-0194-02 ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; 开放科学（资源服务）标识码（OSID）黔南州位于贵州南部，处于云贵高原边缘向广西山地丘陵过渡地带。

区域呈现南北长条性分布，南面和东南面与广西接壤，属于亚热带湿润季风气候，四季分明，冬季天气主要受南下冷空气影响。

农作物主要有茶叶、火龙果、百香果及茶叶等。

在全球气候变化的影响下，人们的生产生活都发生了巨大的改变，因而研究本地气象要素的气候变化特征十分必要。

虽然人类已经累积了较长时期的气象观测资料，对本地的气候也有一定的认识，但对于全州性的气候演变规律及分布尚无明确结论。

因此，需要应用气候分析方法对长年观测积累的气象资料进行统计分析，找出黔南州气候变化规律，以便更好地掌握全球气候变化背景下本地气候受到的影响。

基于M-K检验方法的沈阳地区典型水文站近53年洪水要素演变分析靳明【摘要】结合沈阳地区两个典型水文站近53年洪水要素,结合M-K检验方法对其站点洪水演变趋势进行分析,分析结果表明:东陵站洪峰呈现上升趋势外,其最大1日和最大3日洪量都呈现略递减变化趋势,大河泡站洪峰和洪量都呈现递减趋势,但趋势变化较弱;两个站点峰量关系均较好,相关系数在0.9以上,属于高度相关;东陵站洪峰突变年份在2000年,而洪量突变主要发生在80年代,大河泡站洪峰突变年费在1972年,而洪量突变主要发生2000年代,洪量和洪峰突变特征不同.【期刊名称】《地下水》【年(卷),期】2019(041)002【总页数】3页(P119-120,161)【关键词】M-K检验方法;洪峰变化;洪量变化;演变特征分析;沈阳地区【作者】靳明【作者单位】辽宁省沈阳水文局,辽宁沈阳 110043【正文语种】中文【中图分类】P336对洪水要素演变特征的分析对于区域防洪科学规划十分重要[1]。

当前，人类活动和气候变化的双重影响下[2]，区域洪水要素发生不同程度的变化，急需要对其洪水演变特征进行分析，从而为制定防洪措施提供重要的依据[3]。

当前，对于洪水要素演变特征分析采用的方法为M-K非线性趋势检验方法[4-9]，该方法可以对洪水要素的演变特征进行有效分析。

为此本文结合M-K非线性趋势检验方法，对沈阳地区两个典型站点的洪水特征进行分析，从而为区域的防洪规划提供重要的数据支撑。

1 研究方法1.1 趋势非线性检验方法为对暴雨特征变化趋势进行检验，采用M-K非线性趋势检验方法对朝阳市各短历时强降水的变化特征进行检验，该方法假设时间数据序列(x1，x2，…，xn)为独立、随机同变量分布的样本序列，检验统计变量S计算方程为：(1)当(2)(3)当(4)在上述方程中， S为正态分布的检验统计变量；xi和xj分别为同一样本中不同分布的两个系列，其中1≤j<i≤n；σs表示为标准方差；sign表示为运算符号；n表示为样本的总个数；Z表示为检验值，若Z>0, 检验的时间序列为上升变化趋势，Z<0，检验的时间序列为上下降变化趋势；Z的绝对值大于或等于2.32、1.64、1.28, 表示通过置信度分别为99%、95%以及90%的显著性检验水平。

⽓象数据分析之突变检验及python的实现：MK突变、Pettitt⽅法、滑动T检验⽂章⽬录前⾔：什么是突变？常见的⽓候突变是把它定义为⽓候从⼀个平均值到另 ⼀个平均值的急剧变化, 它表现为⽓候变化的不连续性（符淙斌，1992）。

下图总结了四种常见的突变：(a)均值突变：从⼀个均值到另⼀个均值的变化，表现⽓候变化的不连续性(b)变率突变：平均值没有变但是⽅差变了©跷跷板突变(d)转折突变：某⼀ 时段持续减少 ( 增加 ) , 然后突然在某点开始持续增加 (减少 )检验突变的⽅法有很多，但是啊每种⽅法都有优缺，有可能不同⽅法的检验结果不同，所以建议使⽤多种⽅法进⾏⽐较。

另外，要指定严格的显著性⽔平进⾏检验。

本⽂介绍⼏种常⽤的⽅法，内容均来⾃《现代⽓候统计诊断与预测技术(第⼆版）》（魏凤英 著）。

1. MK突变分析Mann-Kendall法是⼀种⾮参数统计检验⽅法，该类型⽅法亦称为五分部检验，其优点是不需要样本遵从⼀定的分布，也不受到少数异常值的⼲扰，更实⽤于类型变量和顺序变量，计算也⽐较简便。

但是不适⽤于检测有多个突变点的序列。

例图如下，置信区间内（红⾊虚线内）的交点就是突变点，正值代表增长，负值反之from scipy import statsimport numpy as npfrom matplotlib import pyplot as pltdef sk(data):n=len(data)Sk =[0]UFk =[0]s =0E =[0]Var =[0]for i in range(1,n):for j in range(i):if data[i]> data[j]:s = s+1else:s = s+0Sk.append(s)E.append((i+1)*(i+2)/4)# Sk[i]的均值Var.append((i+1)*i*(2*(i+1)+5)/72)# Sk[i]的⽅差UFk.append((Sk[i]-E[i])/np.sqrt(Var[i]))UFk=np.array(UFk)return UFk#a为置信度def MK(data,a):ufk=sk(data)#顺序列ubk1=sk(data[::-1])#逆序列ubk=-ubk1[::-1]#逆转逆序列#输出突变点的位置p=[]u=ufk-ubkfor i in range(1,len(ufk)):if u[i-1]*u[i]<0:p.append(i)if p:print("突变点位置：",p)else:print("未检测到突变点")#画图conf_intveral = stats.norm.interval(a, loc=0, scale=1)#获取置信区间plt.figure(figsize=(10,5))plt.plot(range(len(data)),ufk,label ='UFk',color ='r')plt.plot(range(len(data)),ubk,label ='UBk',color ='b')plt.ylabel('UFk-UBk',fontsize=25)x_lim = plt.xlim()plt.ylim([-6,7])plt.plot(x_lim,[conf_intveral[0],conf_intveral[0]],'m--',color='r',label='95%显著区间') plt.plot(x_lim,[conf_intveral[1],conf_intveral[1]],'m--',color='r')plt.axhline(0,ls="--",c="k")plt.legend(loc='upper center',frameon=False,ncol=3,fontsize=20)# 图例plt.xticks(fontsize=25)plt.yticks(fontsize=25)plt.show()#输⼊数据和置信度即可MK(data,0.95)2. Pettitt⽅法是⼀种与MK⽅法相似的⾮参数检验⽅法。

BFAST--一种分析气候极端事件变化的新方法王烨;李宁;张正涛;张洁【摘要】为了分析北京气候变化对极端事件频次的影响，采用 Mann-Kendall 突变检验方法对北京站1952－2010年年平均温度数据进行突变分析，在不能成功地检测到北京年平均温度的突变情况时，引入 BFAST 方法处理月平均温度时间序列，这是由于月平均温度数据与年数据相比更加精细，灾害或极端事件发生的情况在月数据上有更加良好的反映，得到月平均温度的变化趋势和突变点后，进一步探究北京极端高温事件频次的变化。

研究结果显示，BFAST 监测到的气候变化趋势和突变点与极端高温频次的变化有较好的一致性，它是一个判定气候变化情况和分析气候极端事件的有力工具。

%To analyze the influence of climate change on the frequency of extreme events in Beijing,firstly, Mann-Kendall method is used to deal with annual average temperature data in 1952-2010 of Beijing station.Since abrupt change of the annual average temperature of Beijing was not successfully detected,BFAST is introduced to deal with the monthly average temperature time series,this is because monthly average data is more sophisticated compared with annual average data,diasaster or extreme events can be better reflected on monthly data.The article further explores the changes of the frequency of extreme high temperature events in Beijing after gaining the trend and abrupt change of monthly average data.The results show that the climate change trend and abrupt change which BFAST detected is consistent with the change of the frequency of extreme high temperature events.BFAST is a powerful tool to determine climate change and to analyze climate extremes.【期刊名称】《灾害学》【年(卷),期】2016(031)004【总页数】4页(P196-199)【关键词】M-K突变检验;BFAST方法;气候变化;极端高温事件【作者】王烨;李宁;张正涛;张洁【作者单位】北京师范大学地表过程与资源生态国家重点实验室，北京 100875; 民政部/教育部减灾与应急管理研究院，北京 100875;北京师范大学地表过程与资源生态国家重点实验室，北京 100875; 北京师范大学环境演变与自然灾害教育部重点实验室，北京 100875; 民政部/教育部减灾与应急管理研究院，北京 100875;北京师范大学地表过程与资源生态国家重点实验室，北京 100875; 民政部/教育部减灾与应急管理研究院，北京 100875;北京师范大学地表过程与资源生态国家重点实验室，北京 100875; 民政部/教育部减灾与应急管理研究院，北京 100875【正文语种】中文【中图分类】X43;P4611900年以来, 地球气候正经历一次以全球变暖为主要特征的显著变化。

M-K检验方法原理代码网址降雨、径流分析采用非参数检验方法曼-肯德尔法（Mann-Kendall）检验法来检测泾河合水川流域降水的长期变化趋势和突变情况。

在时间序列趋势分析中，Mann-Kendall检验方法，最初由Mann和Kendall提出，许多学者不断应用Mann-Kendall方法分析降水、径流、气温和水质等要素时间序列趋势变化[6-7]。

Mann-Kendall检验不需要样本遵循一定的分布，也不受少数异常值的干扰，适用于水文、气象等非正态分布的数据，计算方便。

在Mann-Kendall检验中，原假设H0为时间序列数据（X1，…,Xn),是n个独立的、随机变量同分布的样本；备择假设H1 是双边检验，对于所有的k，j≤n，且k≠j，X k 和X j的分布是不相同的，检验的统计量S计算如下式：∑∑=+=-=1-n1kn1kj) SgnkjXXS（其中，⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<-=->-+=-0)(1-0)(001)gn k j k j k j k j X X X X X X X X S ）（（S 为正态分布，其均值为0，方差18/)5n 2(1-n n αr+=）（）（S V 。

当n>10时，标准的正态系统变量通过下式计算： ⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧<+=>=010001-αr αr S S V S S S S V S Z ）（）（这样，在双边的趋势检验中，在给定的α置信水平上，如果α/21-≥Z Z ,则原假设是不可接受的，即在α置信水平上，时间序列数据存在明显的上升或下降趋势。

对于统计量Z ，大于0时是上升趋势；小于0时是下降趋势。

Z 的绝对值在大于等于、1、64和时，分别表示通过了信度90%，95%，99%的显着性检验。

当Mann-Kendall 检验进一步用于检验序列突变时，检验统计量与上述Z 有所不同，通过构造一秩序列： ∑∑==k 1i 1-i j ijk αS （k=2,3,4，…，n ）其中，⎩⎨⎧<>=j i ji ij 01αX X X X 1≤j ≤i定义统计变量： []）（）kk k kαr (S V S E S UF -= （k=1，2, …，n ） 式中：72/)52)(1()(;4/1k )(αr k +-=+=k k k S V K S E k）（ UF k 为标准正态分布，给定显着性水平α，若|UF k |>U α/2 ,则表明序列存在明显的趋势变化，将时间序列x 按逆序排列，再按照上式计算，同时使 ⎩⎨⎧-+=-=k UF UB 1n k k k （k=1,2，…，n ），通过分析统计序列k k UB UF 和可以进一步分析序列x 的趋势变化，而且可以明确突变的时间，指出突变的区域。

多种方法在水文关键要素一致性检验中的比较管晓祥;张建云;鞠琴;王国庆;关铁生【摘要】以武隆站的水文资料作为研究基础,分析了不同的一致性检验方法的特点、适用性以及不足等.结果表明:就趋势性检验方法而言,其过程线法、滑动平均法以及线性拟合法可直接显示序列过程走势,也可通过目估法判断序列走势,但是该方法依赖经验性,不能给出趋势的显著性程度;而作为非参数检验的Mann-Kendall趋势检验法和Spearman秩次相关检验法能确定一定置信水平下的趋势显著性水平;就突变点检验方法而言,双累积曲线法、有序聚类法和M-K突变检验法的结果直观,但双累积曲线一致性关系较为模糊,需配合其他方法一起诊断,有序聚类法计算简单但是检验结果不易评价显著性,均值差异T检验法和M-K突变点检验法可以确定多个突变点;总体而言,M-K检验方法最优,原理清晰,结果直观,便于识别,能检验趋势性和突变性,并可以给出一定置信水平下的检验结果的显著性评价.【期刊名称】《华北水利水电学院学报》【年(卷),期】2018(039)002【总页数】6页(P51-56)【关键词】水文要素;一致性检验方法;趋势性检验方法;突变点检验方法;比较【作者】管晓祥;张建云;鞠琴;王国庆;关铁生【作者单位】河海大学水文水资源学院,江苏南京210098;水利部应对气候变化研究中心,江苏南京210029;南京水利科学研究院水文水资源与水利工程科学国家重点实验室,江苏南京210029;水利部应对气候变化研究中心,江苏南京210029;河海大学水文水资源学院,江苏南京210098;南京水利科学研究院水文水资源与水利工程科学国家重点实验室,江苏南京210029;水利部应对气候变化研究中心,江苏南京210029;南京水利科学研究院水文水资源与水利工程科学国家重点实验室,江苏南京210029;水利部应对气候变化研究中心,江苏南京210029【正文语种】中文【中图分类】TV11气候变化和人类活动是影响流域水文循环过程和水资源演变规律的两大驱动因素，所引起的水文效应已成为当前全球变化研究领域的焦点问题。