邹(Chow)突变点检验
- 格式:doc
- 大小:85.50 KB
- 文档页数:3
一、邹式检验(突变点检验、稳定性检验)1.突变点检验1985—2002年中国家用汽车拥有量(t y ,万辆)与城镇居民家庭人均可支配收入(t x ,元),数据见表6.1。
表6.1 中国家用汽车拥有量(t y )与城镇居民家庭人均可支配收入(t x )数据年份 t y (万辆) t x (元)年份 t y (万辆) t x (元)1985 28.49 739.1 1994 205.42 3496.2 1986 34.71 899.6 1995 249.96 4283 1987 42.29 1002.2 1996 289.67 4838.9 1988 60.42 1181.4 1997 358.36 5160.3 1989 73.12 1375.7 1998 423.65 5425.1 1990 81.62 1510.2 1999 533.88 5854 1991 96.04 1700.6 2000 625.33 6280 1992 118.2 2026.6 2001 770.78 6859.6 1993155.772577.42002968.987702.8下图是关于t y 和t x 的散点图:从上图可以看出,1996年是一个突变点,当城镇居民家庭人均可支配收入突破4838.9元之后,城镇居民家庭购买家用汽车的能力大大提高。
现在用邹突变点检验法检验1996年是不是一个突变点。
H0:两个字样本(1985—1995年,1996—2002年)相对应的模型回归参数相等H1:备择假设是两个子样本对应的回归参数不等。
在1985—2002年样本范围内做回归。
在回归结果中作如下步骤(邹氏检验):1、Chow 模型稳定性检验(lrtest)用似然比作chow检验,chow检验的零假设:无结构变化,小概率发生结果变化* 估计前阶段模型* 估计后阶段模型* 整个区间上的估计结果保存为All* 用似然比检验检验结构没有发生变化的约束得到结果如下;(如何解释?)2.稳定性检验(邹氏稳定性检验)以表6.1为例,在用1985—1999年数据建立的模型基础上,检验当把2000—2002年数据加入样本后,模型的回归参数时候出现显著性变化。


72INTERNATIONAL PETROLEUM ECONOMICS国际石油经济Vol.28, No.122020摘 要:新冠肺炎疫情在全球范围内暴发,持续冲击世界经济,2020年4月20日,美国原油期货价格史无前例地跌至-40.32美元/桶,疫情期间国际原油价格驱动因素值得探讨。
选取2020年1月13日至8月3日交易日数据,考虑结构突变,构建国际原油价格驱动因素断点最小二乘法模型。
经实证,原油价格跌至负值当日确为模型的结构断点,结构断点前新冠肺炎疫情对国际原油价格上涨起严重阻碍作用,投资者预期对国际原油价格上涨也存在消极影响;结构断点后货币政策消极程度严重阻碍国际原油价格上涨;原油需求对原油期货价格的影响在结构断点前后有所不同。
据此认为,疫情防控和提升货币的政策积极性是各国的首要任务,保持对投资者具有重大利好的货币政策倾向、提升信息透明度是促进原油价格提升的重要手段。
关键词:新冠肺炎疫情;国际原油价格;断点最小二乘法;邹突变点检验Abstract :The outbreak of COVID-19 on a global scale continues to impact the world economy. On April 20, 2020, the US crude oil futures price fell to USD -40.32/barrel for an unprecedented time due to the impact of the pandemic. It is worth exploring the driving factors of international crude oil price during the pandemic. The paper selects the trading date of solstice on January 13, 2020 to August 3, considers the abrupt change of structure, and constructs driving factors of international crude oil price—the least square model of the breakpoint. Empirical results show that the day when crude oil price falls to the negative is indeed the structural break point of the model. Before the structural break point, COVID-19 has seriously hindered the rise of international crude oil price, and investor’s expectations also have a negative impact on the rise of international crude oil price. After the structural break point, the degree of monetary policy passivity seriously hinders the rise of international crude oil price. The effect of crude oil demand on crude oil futures price varies before and after the structural break point. Therefore, this paper believes that the prevention and control of the pandemic and the promotion of monetary policy initiatives are the top priorities of all countries in the world, and maintaining a monetary policy orientation that is highly beneficial to investors and improving information transparency are also important means to promote the increase of international crude oil prices.Key words :the COVID-19; international crude oil price; least square with breakpoint; Chow breakpoint test新冠肺炎疫情下国际原油价格驱动因素研究——基于断点最小二乘法与邹突变点检验闫勇1,张雪峰2,宋鸽2,付杨3( 1.中国石油集团经济技术研究院;2.北方工业大学经济管理学院;3.北京石油机械有限公司)Research on the driving factors of international crude oil price under COVID-19—Based on least square with breakpoint and Chow breakpoint test YAN Yong 1, ZHANG Xuefeng 2, SONG Ge 2, FU Yang 3(1. CNPC Economics &Technology Research Institute; 2. School of Economics and Management, North China University of Technology; 3. CNPC Beijing Oilfield Machinery Co., Ltd.)FORUM油价论坛731 国际原油价格驱动因素及相关研究2020年初,新型冠状病毒肺炎(下文简称“新冠”)疫情在全球范围内暴发。

1.突变点检验1985—2002年中国家用汽车拥有量(t y ,万辆)与城镇居民家庭人均可支配收入(t x ,元),数据见表。
表 中国家用汽车拥有量(t y )与城镇居民家庭人均可支配收入(t x )数据年份 t y (万辆) t x (元)年份 t y (万辆) t x (元)198519941986 1995 4283 1987 1996 1988 1997 1989 1998 1990 1999 5854 1991 2000 6280 1992 2001 19932002下图是关于t y 和t x 的散点图:从上图可以看出,1996年是一个突变点,当城镇居民家庭人均可支配收入突破元之后,城镇居民家庭购买家用汽车的能力大大提高。
现在用邹突变点检验法检验1996年是不是一个突变点。
H 0:两个字样本(1985—1995年,1996—2002年)相对应的模型回归参数相等 H 1:备择假设是两个子样本对应的回归参数不等。
在1985—2002年样本范围内做回归。
在回归结果中作如下步骤(邹氏检验):1、 Chow 模型稳定性检验(lrtest )用似然比作chow 检验,chow 检验的零假设:无结构变化,小概率发生结果变化 * 估计前阶段模型* 估计后阶段模型* 整个区间上的估计结果保存为All* 用似然比检验检验结构没有发生变化的约束得到结果如下;(如何解释)2.稳定性检验(邹氏稳定性检验)以表为例,在用1985—1999年数据建立的模型基础上,检验当把2000—2002年数据加入样本后,模型的回归参数时候出现显著性变化。
* 用F-test作chow间断点检验检验模型稳定性* chow检验的零假设:无结构变化,小概率发生结果变化* 估计前阶段模型* 估计后阶段模型* 整个区间上的估计结果保存为All* 用F检验检验结构没有发生变化的约束*计算和显示 F检验统计量公式,零假设:无结构变化然后dis f_test则得到结果;* F统计量的临界概率然后得到结果* F统计量的临界值然后得到结果(如何解释)二、似然比(LR)检验DEBT,亿元)模型如下:有中国国债发行总量(t0123t t t t t DEBT GDP DEF REPAY u ββββ=++++其中t GDP 表示国内生产总值(百亿元),t DEF 表示年财政赤字额(亿元),t REPAY 表示年还本付息额(亿元)。

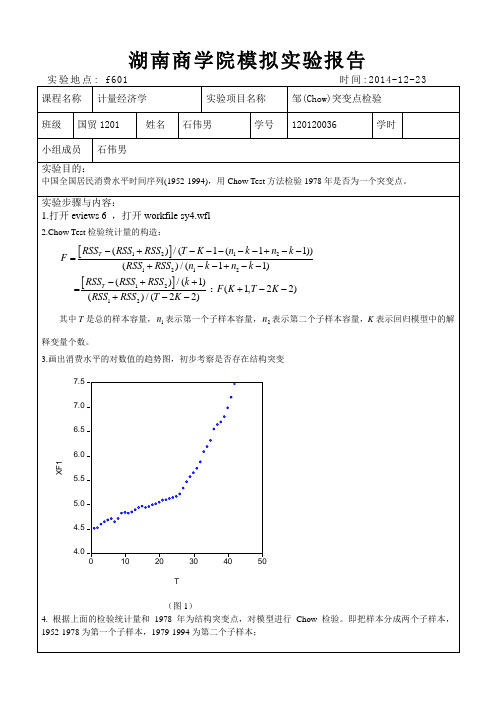
数学与统计学院实验报告院(系):数学与统计学学院学号:姓名:实验课程:计量经济学指导教师:实验类型(验证性、演示性、综合性、设计性):验证性实验时间:2017年 3 月15 日一、实验课题Chow检验(邹氏检验)二、实验目的和意义1 建立财政支出模型表1给出了1952-2004年中国财政支出(Fin)的年度数据(以1952年为基期,用消费价格指数进行平减后得数据)。
试根据财政支出随时间变化的特征建立相应的模型。
表1obs Fin obs Fin obs Fin19521970198819531971198919541972199019551973691199119561974199219571975199319581976199419591977199519601978199619611979199719621980199819631981199919641982200019651983200119661984200219671985200319681986200419691987步骤提示:(1)做变量fin的散点图,观察规律,看在不同时期是否有结构性变化。
(2)建立时间变量t=1,2,…,做Fin关于t的线性回归模型,并对其做参数结构稳定性检验(Chow检验或Chow预测检验)(建立变量t的方法是:t=@trend()+1)三、解题思路(1)Eviews6---建立fin的连续序列(object--series)---画散点图(view—graph—dot plot)(2)建立t的时间变量(quick—generate series—t=@trend()+1)---建立fin、t的方程(quick--estimate equation—fin c t)---chow检验(view—stability test—chow breakpoint test—断点为1996)---建立三个方程(一个受约束方程,两个不受约束方程)---比较1996年属于不受约束方程那个方程四、实验过程记录与结果(1)、散点图通过散点图可以发现,1996年存在结构性变化(针对斜率96年前后突然变大)(2)chow检验受约束模型:由该方程发现,残差存在明显的相关性,即存在自相关性,进行以1996年为断点分阶段检验不受约束模型(1)、1952-1996(2)1997-2004根据受约束模型相比,各统计量明显有转好的趋势。
邹至庄(Gregory C. Chow )检验比较两个回归 :检验模型的结构稳定性所谓模型的结构稳定的指模型在样本期的不同时期(子样本),其参数不发生改变。
而任何参数样本期的不同时期发生改变,则称模型不具有结构稳定性。
一般而言,导致模型发生结构变化的因素是重要的外生事件,或外生冲击,故常设定某一时点或年份,以此将样本分为二个子样本,分别估计这二个子样本和样本全体,构成F 统计量,据此推断模型是否发生结构变化。
例子:美国个人收入和储蓄(样本1970-1995)。
由于美国在1982年失业率达到8.2%,为检验这一高失业率是否导致个人储蓄行为发生变化,将1981年设定为一个可能的结构变化点,将样本分为1970-1981和1982-1995,并设定这两个时期的储蓄函数为t t t u x Y 121++=αα (1))1954(,,2,11==n t Λt t t u x Y 221++=ββ (2))1963(,,2,12==n t ΛCHOW 检验:假设 ),0(~2σN u i ,0)(.2,121==u u E i ;1.用全体样本(211,1,,2,1n n n t ΛΛ+=)对模型t t t u x Y ++=21λλ (3)进行OLS ,得到RSS ,其自由度为))2((21=-+k n n ,并记为S R ;这里下标R 表示将两个子样本的回归参数约束为相等2.用2个子样本分别估计(1)和(2),且分别记RSS 为S 1和S 2;其自由度分别为k n -1和k n -2。
定义45214S S S S S S R -=+= 其自由度分别为k k k n n )),2(2(21=-+。
3.构造CHOW 的F 统计量,在上述假设下,有)2,(~)2/(/212145k n n k F k n n S k S F -+-+= (4) 以此检验原假设:无结构变化,备选假设:模型具有结构变化(任意参数).特别强调,结构变化检验,不是对于不同的子样本的估计进行比较,而是计算(4)的F 值进行推断。