人教版小学五年级上册数学多边形的面积--爬坡题

人教版五年级上册数学多边形面积应用题1、做一块底是12米，高是8米的三角形广告牌，共用720元铁皮，平均每平方米铁皮多少元？2、一块三角形地的底是16米，高是8米，共收萝卜512千克，这块地平均每平方米收萝卜多少千克？3、一个面积是384平方米的平行四边形苗圃，底是24米，高是多少米？4、油漆如下图所示的广告牌，如果每平方米的成本是5元，那么一共需要多少钱？5、一块三角形钢板的底边长24厘米，高15厘米，如果每平方厘米钢板重20克，这块钢板重多少千克？6、一块梯形地，它的上底是100米，下底是150米，高是80米，这块地的面积是多少平方米？7、一个平行四边形的停车场，底是63米，高是25米。

平均每辆车占地15平方米，这个停车场可停车多少辆？8、一块梯形的铁皮，上、下底的和是25厘米，高是22厘米，这块铁皮的面积是多少平方厘米？9、一块梯形牡丹园的上底是12米，下底是16米，高是2米。

这个牡丹园一共种了56棵牡丹，平均每平方米种多少棵牡丹？10、如图平行四边形菜地里，种萝卜的面积是青椒面积的2倍。

（1）青椒种了多少平方米？（2）这块平行四边形菜地共有面积多少平方米？11、一块三角形纸板的底是12.6cm，高比底长2.4cm。

求三角形纸板的面积。

12、一个三角形的底长6米，如果底缩短1米，那么面积就减少1.5平方米。

那么原来三角形的面积是多少平方米？13、一个平行四边形，若高增加4厘米，底不变，则面积增加48平方厘米；若底减少4厘米，高不变，则面积减少40平方厘米。

原平行四边形的面积是多少平方厘米？14、一块菜地一面靠墙，用62米的篱笆刚好把菜地的三条边围起来（如图），这块菜地的面积是多少平方米？15、已知一个平行四边形的面积是227.5平方分米，它的底长18.2分米，它的高比底少多少分米？16、一块平行四边形钢板，底长8dm, 高6dm。

每平方分米钢板重0.4千克，这块钢板重多少千克？17、下图是一块长方形草地，长方形的长是16，宽是10，中间有两条道路，一条是长方形，一条是平行四边形，那么，有草部分（阴影部分）的面积有多大？（单位：米）18、如图所示，已知直角梯形ABCD的高是30厘米，且∠1 = ∠2 = 45 ∘，∠DEC = 90 ∘，则梯形ABCD 的面积是多少平方厘米？19、如图，一个三角形的底长5米，如果底延长1米，那么面积就增加1.5平方米。

（常考题）新人教版小学数学五年级上册第六单元多边形的面积测试题（含答案解析）(1)一、选择题1．一个梯形的上底、下底各扩大到原来的10倍，高不变，这个梯形的面积（）。

A. 扩大到原来的10倍B. 扩大到原来的20倍C. 扩大到原来的100倍2．如图，每个小方格的面积是1平方厘米，估一估，这个脚印的面积大约是（）平方厘米。

A. 13B. 20C. 35D. 403．下面不是运用转化思想方法的是（）。

A. 计算7.65÷0.85时，将其看成765÷85来算。

B. 计算2.4×0.8时，先算24×8＝192，再算192÷100＝1.92。

C. 推导平行四边形面积公式，把平行四边形沿着高剪拼成一个长方形。

D. 计算“一个长是2.4dm，宽是2dm”的长方形的面积”，列式为：2.4×2。

4．如图：平行线间的三个图形，它们的面积相比（）A. 三角形的面积大B. 梯形的面积大C. 平行四边形的面积大D. 面积都相等5．如图的梯形中，两个阴影部分的面积相比，（）A. S1＞S2B. S1＜S2C. S1＝S2D. 无法确定6．图中甲的面积是50cm2，乙的面积是（）A. 25cm2B. 30cm2C. 50cm27．下图中阴影部分的面积（）空白部分的面积。

A. 大于B. 小于C. 等于D. 无法确定8．一个梯形的上底是acm，下底是3cm，高是bcm，那么它的面积是（）。

A. （a+b）×3B. （a+b）×3÷2C. （a+3）×b×2D. （a+3）×b÷2 9．三角形与平行四边形的底和面积都相等。

已知平行四边形的高是5厘米，三角形的高应是（）。

A. 5厘米B. 10厘米C. 15厘米10．如图，阴影部分的面积与空白部分的面积相比较，它们（）。

A. 相等B. 不相等C. 无法确定11．底和高分别相等的两个平行四边形（）。

人教版五年级上册数学第六单元《多边形面积》同步练习题一.选择题1.一个梯形的上底增加2厘米，下底减少2厘米，高不变，它的面积与原面积相比（）。

A.变大了B.变小了C.不变D.高不知道，所以无法比较2.等底等高的两个三角形（）。

A.形状相同B.周长相等C.面积相等3.下图平行四边形的面积计算正确的是（）。

A.15×4B.6×15C.6×44.一个长方形框架，把它拉成平行四边形，面积与原来长方形的面积比较（）。

A.变大B.变小C.不变5.如图所示两个完全相同的长方形中，阴影部分的面积相比，甲（）乙。

A.大于B.小于C.相等D.无法确定二.判断题1.从平行四边形中剪一个最大的三角形，三角形的面积占平形四边形面积的。

（）2.用同样长的铁丝围成的平行四边形的面积相等。

（）3.有一块长6米、宽2.5米的黄布，要做成直角边都是0.2米的小三角形的小旗，可以做720面。

（）4.任意一个平行四边形都可以分成两个大小和形状都一样的梯形。

（）5.一个正方形可以分割成两个等边三角形。

（）三.填空题1.拼成平行四边形的两个三角形（）。

2.一个三角形的面积是4.8平方厘米，与它等底等高的平行四边形的面积是（）平方厘米。

3.沿着平行四边形的一条高剪开，然后拼成一个长方形，这个长方形的长等于平行四边形的（），长方形的宽等于平行四边形的（）。

因此，平行四边形的面积等于（），用字母表示是（）。

4.一个等腰直角三角形的直角边是9厘米，它的面积是（）平方厘米。

5.一个长12厘米、宽6厘米的长方形，需要（）个边长是2厘米的小正方形才能把这个长方形正好摆满。

四.计算题1.求下面图形中涂色部分的面积。

（单位：厘米)2.计算下列图形的面积。

（单位：厘米）五.作图题1.求下面各图形的面积。

（单位：cm）1. 2.六.解答题1.如图，一个平行四边形的一边长15厘米，这条边上的高为6厘米，一条线段将此平行四边形分成了两部分，它们的面积相差18平方厘米，求其中梯形的上底是多少厘米？2.果农要在一块底是93米，高是15米的平行四边形土地上栽果树，如果每棵果树树苗占地4.5平方米，那么这块土地一共能栽多少棵树？3.一堆水泥电线杆堆成一个梯形，最上层有4根，最下层有12根，一共有9层。

人教版小学五年级上册第六章多边形的面积知识点及习题(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（人教版小学五年级上册第六章多边形的面积知识点及习题(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为人教版小学五年级上册第六章多边形的面积知识点及习题(word版可编辑修改)的全部内容。

五年级上册第六章多边形的面积1、长方形: 周长=(长+宽)×2——【长=周长÷2-宽；宽=周长÷2—长】字母表示：C=(a+b）×2面积=长×宽字母表示：S=ab2、正方形：周长=边长×4字母表示:C=4a面积=边长×边长字母表示：S=a23、平行四边形：面积=底×高字母表示： S=ah4、三角形的面积=底×高÷2 ——【底=面积×2÷高；高=面积×2÷底】字母表示： S=ah÷25、梯形的面积=(上底+下底）×高÷2字母表示： S=（a+b)h÷2上底=面积×2÷高－下底,下底=面积×2÷高—上底；高=面积×2÷（上底+下底)6、平行四边形面积公式推导：剪拼、平移、割补法7、三角形面积公式推导：旋转、拼凑法平行四边形可以转化成一个长方形；两个完全一样的三角形可以拼成一个平行四边形，长方形的长相当于平行四边形的底；平行四边形的底相当于三角形的底；长方形的宽相当于平行四边形的高；平行四边形的高相当于三角形的高；长方形的面积等于平行四边形的面积,平行四边形的面积等于三角形面积的2倍，因为长方形面积=长×宽，所以平行四边形面积=底×高.因为平行四边形面积=底×高，所以三角形面积=底×高÷28、梯形面积公式推导：旋转、拼凑法9、两个完全一样的梯形可以拼成一个平行四边形;平行四边形的底相当于梯形的上下底之和;平行四边形的高相当于梯形的高；平行四边形面积等于梯形面积的2倍，因为平行四边形面积=底×高，所以梯形面积=(上底+下底)×高÷210、等底等高的平行四边形面积相等；等底等高的三角形面积相等；等底等高的平行四边形面积是三角形面积的2倍.11、长方形框架拉成平行四边形，周长不变，面积变小。

人教版小学五年级数学上册多边形的面积练习题(有答案)第六单元：多边形的面积第一课时：平行四边形的面积测试题基础碰碰车1.填一填1) 1平方米 = (100)平方分米 = ()平方厘米2) 把一个平行四边形转化成长方形，它的面积与原来的平行四边形的面积(相等)。

转化后长方形的长与平行四边形的(底)相等，宽与平行四边形的(高)相等。

3) 平行四边形的面积 = (底) × (高)，字母公式为(S = ah)4) 一个平行四边形的底是8.5米，高是3.4米，求其面积的算式是(8.5 × 3.4)5) 等底等高的两个平行四边形的面积(相等)。

2.判断1) 形状不同的两个平行四边形面积一定不相等(×)。

2) 周长相等的两个平行四边形面积一定相等(×)。

3) 知道一个平行四边形的底和其对应的高的长度就能求出它的面积(√)。

3.一块平行四边形的玻璃，底是50厘米，高是24厘米，它的面积是多少？S = 50 × 24 = 1200(平方厘米)升级跷跷板4.有一个平行四边形的面积是56平方厘米，底是7厘米，高是多少厘米？因为S = ah，所以h = S ÷ a = 56 ÷ 7 = 8(厘米)5.一块平行四边形的菜地，底是36米，高是25米，每平方米收白菜8千克，这块地共收白菜多少千克？S = 36 × 25 = 900(平方米)共收白菜 = S × 8 = 900 × 8 = 7200(千克)6.一个平行四边形的果园，底是30米，高是15米，中了90棵梨树，平均每棵梨树占地多少平方米？每棵梨树占地 = S ÷ n = (30 × 15) ÷ 90 = 5(平方米)智慧摩天轮7.已知下图中正方形的周长是36厘米，求平行四边形的面积。

正方形的边长 = 36 ÷ 4 = 9(厘米)平行四边形的底 = 9(厘米)平行四边形的高 = 9(厘米)平行四边形的面积 = 底 ×高 = 9 × 9 = 81(平方厘米)8.一块平行四边形的铁皮的周长是82厘米，一条底长是16厘米，这条底上的高是20厘米，求另一条底上的高是多少厘米？平行四边形的周长 = 82(厘米)两条底的长度之和 = 82 ÷ 2 = 41(厘米)已知一条底长为16厘米，所以另一条底长为25(厘米)因为S = ah，所以另一条底上的高 = S ÷ b = (16 × 20) ÷ 25 = 12.8(厘米)第六单元：多边形的面积第二课时：三角形的面积测试题快乐研究1.填一填1) 两个(全等)的三角形可以拼成一个平行四边形。

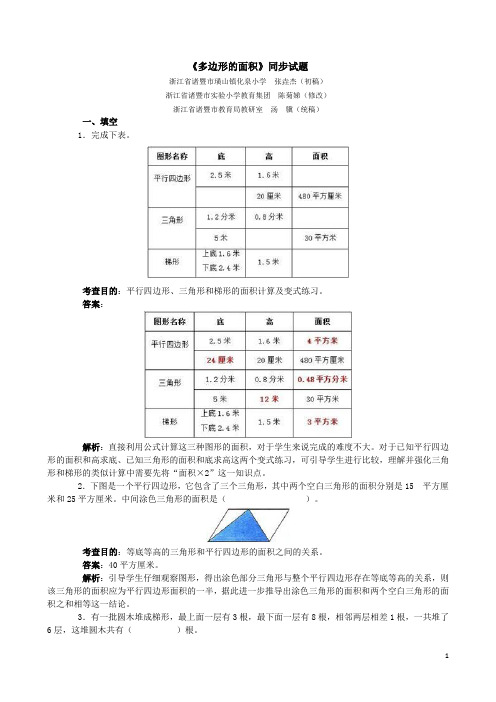
《多边形的面积》同步试题浙江省诸暨市璜山镇化泉小学张垚杰（初稿）浙江省诸暨市实验小学教育集团陈菊娣（修改）浙江省诸暨市教育局教研室汤骥（统稿）一、填空1．完成下表。

考查目的：平行四边形、三角形和梯形的面积计算及变式练习。

答案：解析：直接利用公式计算这三种图形的面积，对于学生来说完成的难度不大。

对于已知平行四边形的面积和高求底、已知三角形的面积和底求高这两个变式练习，可引导学生进行比较，理解并强化三角形和梯形的类似计算中需要先将“面积×2”这一知识点。

2．下图是一个平行四边形，它包含了三个三角形，其中两个空白三角形的面积分别是15 平方厘米和25平方厘米。

中间涂色三角形的面积是（）。

考查目的：等底等高的三角形和平行四边形的面积之间的关系。

答案：40平方厘米。

解析：引导学生仔细观察图形，得出涂色部分三角形与整个平行四边形存在等底等高的关系，则该三角形的面积应为平行四边形面积的一半，据此进一步推导出涂色三角形的面积和两个空白三角形的面积之和相等这一结论。

3．有一批圆木堆成梯形，最上面一层有3根，最下面一层有8根，相邻两层相差1根，一共堆了6层，这堆圆木共有（）根。

考查目的：运用梯形的面积计算方法解决相关的实际问题。

答案：33。

解析：根据“（顶层根数+底层根数）×层数÷2”进行解答。

在此基础上，可引导学生用不同的方法对结果加以验证，重点分析采用等差数列求和的方法即“（首项+末项）×项数÷2”，这既是解决该题的基本数学模型，也能突出体现“数形结合”的思想。

4．如图的小花瓶中，1个小正方形的面积是1平方厘米，那么整个花瓶的面积是（）平方厘米。

考查目的：组合图形的面积计算。

答案：5。

解析：通过转化，小花瓶左右两侧的部分可以组合成两个小正方形，再加瓶身的部分即可。

也可采用计算的方法，由题意可得一个小正方形的边长为1厘米，则花瓶两边三角形的面积之和为2×1÷2×2=2（平方厘米），整个花瓶的面积为2+3=5（平方厘米）。

小学数学五年级上册人教版第六单元多边形的面积测试（包含答案解析）一、选择题1．如图中，A、B和C三个图形的面积相比较，（）A. A＝BB. A＝CC. B＝CD. A＝B＝C 2．如图，如果一个梯形的上底和下底都向右延长2dm，变成一个新的梯形，新的梯形的面积比原来梯形的面积增加（）。

A. 12dm2B. 6dm2C. 3dm2D. 无法计算3．如图，在边长相等的三个正方形中，关于三角形S1和S2面积大小的说法中正确的是（）。

A. S1>S2B. S1<S2C. S1=S2D. 不确定4．一个直角三角形的三条边长分别是6cm，8cm，10cm，这个三角形的面积是（）。

A. 24cm2 B. 30cm2 C. 40cm2 D. 48cm25．一个三角形的底不变，要使面积扩大2倍，高要扩大（）A. 2倍B. 4倍C. 6倍D. 8倍6．一个三角形的面积是24平方厘米，高是8厘米，与这条高对应的底是（）。

A. 1.5厘米B. 3厘米C. 6厘米D. 9厘米7．一堆钢管最上层有14根，最下层有26根。

每层相差1根，共有13层，这堆钢管共有（）根。

A. 260B. 240C. 220D. 2108．一个梯形的面积是84cm2，上底和下底的长度之和是7cm，它的高是（）。

A. 24cmB. 12cmC. 48cmD. 36cm 9．一个三角形和一个平行四边形的底和面积都相等，那么三角形的高（）A. 和平行四边形的高相等B. 是平行四边形高的一半C. 是平行四边形高的2倍D. 是平行四边形高的4倍10．如图，4个完全相同的正方形拼成一个长方形，图中阴影部分的面积大小关系是（）。

A. 甲>乙>丙B. 乙>甲>丙C. 甲=乙=丙11．一个直角三角形，直角所对的边长是10厘米，其余两边分别是8厘米和6厘米，这个三角形的面积是（）平方厘米。

A. 40B. 30C. 2412．下图平行线间的三个图形的面积相比较，（）。

北师大5数下爬坡题第一单元 分数加减法例1 如下图，已知各种图形的面积都相等，那么可以在“=”后面表示阴影部分面积运算结果的是（ ）。

【详解】 根据分数的意义，题目中第一个图形是把圆的面积看作单位“1”，平均分成4份，阴影部分占了3份，即阴影部分面积是圆面积的43；第二个图形是把正方形的面积看作单位“1”，平均分成2份，阴影部分占了1份，即阴影部分面积是正方形面积的21；第三个图形是把三角形的面积看作单位“1”，平均分成了4份，而阴影部分占其中的1份，即阴影部分面积是三角形面积的41。

又因为三种图形的面积都相等，所以题中阴影部分面积可以用算式43-21+41=21表示，结果是21。

【答案】21 例2 不用通分母，比较95和136的大小。

方法一：通分子比较分数的大小。

【详解】95和136的分子和分母都不相同，无法直接比较它们的大小，可以根据分数的基本性质把分数化成分子相同的分数进行比较。

即：5430696595=⨯⨯=，653051356136=⨯⨯=，分子相同，分母小的分数大，所以65305430>，所以95>136。

【答案】5430696595=⨯⨯=，653051356136=⨯⨯=，因为65305430>，所以95>136。

方法二：借助中间量比较。

【详解】因为95和136的分子都接近分母的一半，可以借助21进行比较。

95表示把单位“1”平均分成9份，取其中的5份，而9份的一半是4.5份，所以95>21；136表示把单位“1”平均分成13份，取其中的6份，而13份的一半是6.5份，所以136<21。

【答案】因为95>21，136<21，所以95>136。

例3 把 0.33……和 0.4747…… 化成分数。

【详解】纯循环小数的循环节最少位数是几，分母就是由几个9组成的数；分子是纯循环小数中一个循环节组成的数。

0.33……×10＝3.33……0.33……×10－0.33……=3.33……－0.33……=3=（10-1）×0.33……即9×0.33……=3 那么0.33……=93=31 0.4747……×100=47.4747……0.4747……×100－0.4747……=47.4747……－0.4747……=47= (100－1)×0.4747……即99×0.4747……=47 那么 0.4747……=9947 【答案】0.33……=31 0.4747……=9947 第二单元 长方体（一）例1 用丝带捆扎一种礼品盒（如下图），接头处长25厘米，要捆扎这种礼品盒需准备（ ）的丝带比较合理。

五年级上册数学人教版6 《多边形的面积》操作题专项练习（含答案）五上《多边形的面积》作图题专项练习学校:___________姓名：___________班级：___________考号：___________1．如图，在方格纸上找一个点C，连接AB、AC和BC后得到一个三角形，且使三角形的面积为2平方厘米。

2．（1）画出将三角形先向下平移3格，再向右平移4格后的图形B。

（2）以虚线a为对称轴，画出平移后图形B的轴对称图形C。

（3）画一个与三角形面积相等的梯形。

3．按要求画图。

（每小格都是边长为1厘米的正方形）。

（1）在下面的方格图中画出一个面积为12平方厘米的平行四边形。

（2）画出一个与平行四边形面积相等的钝角三角形。

（3）画出一个与平行四边形面积相等的梯形。

4．（1）请你在方格纸中用直尺画一个与图中平行四边形面积相等的三角形；（2）请你在方格纸中用直尺画一个与图中平行四边形面积相等的梯形。

5．在方格中按要求画出图形。

（小正方形的边长为1cm）（1）请你画出△向下平移四格，再向左平移两格的图形。

（2）以△的边为底，再画出一个和△面积相等的三角形。

（3）小明把两个完全一样的梯形DEFG拼成了两种不同的图形。

请你画出这两个图形，要求一个是轴对称图形，另一个不是轴对称图形。

（4）请你画出到线段a的距离等于1cm的所有的点。

6．在图中的平行线间，画出与三角形面积相等的平行四边形、梯形各一个，并标出底的长度（每小格表示1厘米）。

7．画一个面积为12cm2的平行四边形。

（图中每个小方格的面积是1cm2）8．如图，是把一个平行四边形等分成面积相等的三份的一种方法（提示：图1和图2是同一种分法，因为它们分的思路相同）。

请你再用三种不同的思路设计3种分法（不同于第一种分法），分别把下面3个平行四边形等分成面积相等的三份。

9.按要求画图形。

（每个小方格的边长都表示1厘米）（1）画一个面积是12平方厘米，高是3厘米的平行四边形。

2023-2024学年人教版五年级数学上同步复习题：多边形的面积一．选择题（共4小题）1．如图平行四边形的面积是( )A ．27cmB ．28cmC ．29cmD ．210cm2．已知一个三角形两边的长度分别是9厘米、12厘米，那么，这个三角形的周长可能是()厘米。

A ．24B ．30C ．42D ．453．一个面积是65平方厘米的梯形，上底是5厘米，下底是8厘米，它的高是( )厘米。

A ．5B ．10C ．204．如图，三个图形A 、B 、C 的面积，按从大到小排列是( )A ．A CB S S S >>B ．2C A S S S >>C ．A B c S S S >>D ．C B A S S S >>二．填空题（共4小题）5．一个梯形的上底是2m ，下底是5m ，高是1.8m ，它的面积是 2m 。

6．在梯形ABCD 中，上底长5厘米，下底长10厘米，20BOC S =平方厘米，则梯形ABCD 的面积是 平方厘米。

7．一块平行四边形草坪的高是15m ，底是9.6m ，它的面积是 2m ，每平方米草坪的价格是12元，种这片草坪用了 元。

8．一个梯形的上底与下底的和是18厘米，高是6厘米，面积是 平方厘米。

两个这样的梯形拼成一个平行四边形，平行四边形的面积是 平方厘米。

三．计算题（共3小题）9．求平行四边形的面积。

10．算一算下面组合图形的面积。

（单位：厘米）11．计算下面图形的面积。

（单位：)cm四．应用题（共4小题）12．等腰三角形的周长是80厘米，它的一条腰长24厘米，那么，它的底边长多少厘米？13．如图，一个长方形框架拉成平行四边形后，面积是218dm，长方形框架的周长是多少分米？14．把一个边长是6分米的正方形铁丝框架拆开，用这些铁丝围成一个最大的等边三角形，这个等边三角形的边长是多少分米？15．有一块梯形的果园，它的上底是70米，下底是110米，高80米。