最新新人教版圆柱的体积解决问题例7

把握数量关系教学，聚焦核心素养发展——以人教版六下《圆柱体积的应用》为例《义务教育数学课程标准（2022版）》指出数学学习要引导学生在真实情境中发现问题和提出问题，培养学生发现、提出、分析和解决问题的能力。

当学生遇到问题时，他们尝试借助图形描述和分析问题，从而更好地解决问题，实际上就是他们对题目有了自己的理解。

数学学习需要学生运用逻辑思维，而这个分析的过程能够逐步培养学生的逻辑思维和应用意识，提升学生思维品质，是学生思维提升的一个重要推进过程。

“数量关系”作为数与代数领域的重要主题内容，是小学数学数与代数学习的重要领域。

人教版六年级下册《圆柱体积的应用》一课的教学，是学生经历从现实情境中抽象出数学问题并进行解决，构建数学问题直观模型的课例。

本节课作为发展学生几何直观和应用意识的有效载体，学生要经历借助图形分析和解决问题的过程，思维发展得到一次跨越。

在教学中，笔者创设独特情境，让学生合作探究，给予学生充足的探究空间，在思维过程中构建数学问题的直观模型，探索解决问题的思路。

一、巧妙转化，几何直观促模型建构六年级学生的思维发展水平开始由具体形象思维向具体抽象思维过渡，教学时，要以学生的思维发展水平为基础，在导入环节，注重创设贴近学生生活的情境，激发学生的学习兴趣；例如：《圆柱体积的应用》一课中由于教科书中的情境比较单薄，在创设情境时，可以结合实际，关注学生的兴趣特点，老师拿出一瓶饮料展示，并当场喝掉一部分，让学生根据这一过程提出数学问题。

学生可能提出以下问题：（1）瓶子里还有多少饮料？（剩下多少饮料？）（2）老师喝了多少饮料？（也就是瓶子的空气部分。

）（3）这个瓶子一共能装多少饮料？（也就是这个瓶子的容积是多少？）通过创设情境让学生结合身边经历，唤醒学生的生活经验，激发学生的学习兴趣，调动学生积极探索新知。

教学时，给予学生充足的探索时间和空间，对于问题1：学生很容易发现瓶子里剩下的水呈圆柱状，只要测量出这个圆柱的底面直径和高就能算出它的体积；问题2：学生会发现喝掉部分形状是不规则的，没有办法直接计算，教师注意引导学生发现：在瓶子倒置前后，空气的体积不变，利用水的流动性成功地将不规则的空气部分转化成了一个圆柱体，得到所需数据后就能求出它的体积。

解决问题第1关练速度1.填一填。

（1）求圆柱形水桶能装水多少升，是求它的（）；做一个圆柱形水桶要多少铁皮，是求它的（）。

（2）已知一个正方体、一个长方体与一个圆柱的底面周长相等，高也相等，则它们的体积相比，（）的体积大。

（3）有两个底面积相等的圆柱，一个圆柱的高是6cm，体积是18.84cm³；另一个圆柱的高是10cm，体积是（）cm³。

2.一个圆柱形的玻璃杯，测得底面内直径是8cm，内装药水的深度是16cm，正好占杯内容积的80%，这个玻璃杯的容积是多少毫升？3.如图是一个酸奶瓶，它的瓶身呈圆柱形（不包括瓶颈），底面直径是6cm。

当瓶子正放时瓶内酸奶高为10cm，瓶子倒放时，空余部分高为2cm。

（1）瓶子里酸奶的体积倒置后没变，酸奶的体积加上（）cm高的圆柱的体积就是酸奶瓶的容积。

（2）算一算，酸奶瓶的容积是多少毫升？4.一个水龙头的内直径是1.4cm，打开水龙头后水的流速是25cm/s。

淘气洗手后没有关闭水龙头，10分钟后被发现并关闭，淘气浪费了多少水？第2关练准确率5.输液100m，每分钟输2.5mL，如图是刚过12分钟时吊瓶的数据，求整个吊瓶的容积是多少毫升。

6.把一个底面半径为5cm的圆柱形铁块放入个底面半径为10cm，高为14cm的圆柱形容器里，完全浸没在水中，水面上升了3cm，求这个圆柱形铁块的体积。

7.一支牙膏出口处直径是5mm，小红每次刷牙都挤出1cm长的牙膏。

这支牙膏可用36次。

现将出口处的直径改为6mm，小红还是按习惯每次挤出1cm长的牙膏。

这样这支牙膏能用几次？8下面三个图形的面积都是16cm²（图中的单位：cm）。

用这些图形分别卷成圆柱（图形的宽作为圆柱的高），可以卷成体积最小的圆柱的图形是（），可以卷成体积最大的圆柱的图形是（）。

9.有甲、乙两个圆柱形容器，从里面量得它们的底面半径分别为10cm和5cm，两个容器内分别盛有深10cm和15cm的水，现将乙容器中的一部分水倒入甲容器内，使得两个容器里的水面相平，这时水深多少厘米？第3关练思维10.如图，有一个高为8cm、容积为50mL的圆柱形容器A，里面装满了水。

六年级数学下册期末-圆柱的体积《解决问题》专项练习（人教版，含解析）学校:___________姓名：___________班级：___________考号：___________1．一个圆柱形汽油箱，从里面测量底面直径是6dm，高是7dm，这个油箱最多能装多少升汽油？（得数保留整数）2．有一张长方形的铁皮（如图），剪下图中的阴影部分，正好可以做一个底面直径为4分米的圆柱形油桶。

（1）原来的长方形铁皮面积是多少平方分米？（2）做成的这个圆柱形油桶的容积是多少立方分米？3．一个圆柱形水池，直径是20米，深是直径的14，求：（1）在水池的侧面和池底抹上水泥，求抹水泥部分的面积。

（2）这个水池能蓄水多少立方米？请你算一算每枚1元硬币的体积大约是多少立方厘米？（π取近似值3，结果保留整数）5．一个圆柱形玻璃容器的底面直径是8cm，把一块完全浸泡在这个容器水中的铁块取出后，水面下降3cm。

这块铁块的体积是多少？6．有块正方体的木料，它的棱长是4dm，把这块木料加工成一个最大的圆柱。

这个圆柱体积比原来正方体体积少了百分之几？7．一个圆柱形的粮仓，从里面量得底面直径是4米，装有2.5米高的小麦。

如果每立方米小麦重710吨，这个粮仓装有多少吨的小麦？8．如下图，有高度相同的甲、乙两个圆柱形容器，从里面量，底面积分别是60cm2、75cm2，甲容器中装满水，乙容器是空的。

把甲容器中的水全部倒入乙容器中，则乙容器中的水深比甲容器中的水少了5cm。

问甲圆柱形容器的容积是多少cm3？（列方程解）9．小拓家面盆的容积是8L，他家自来水管内直径是2厘米。

若水管内水流速度是8厘米/秒，小拓打开水龙头，5分钟能否将面盆放满水？10．一个圆柱形玻璃杯的底面直径是8厘米，把一块铁浸没在水中，水面上升了2厘米，这块铁的体积是多少？11．一个注满水的圆柱形水池，底面直径是10米，用去一部分水后，水面下降了40厘米，剩下的水正好是这池水的78。

2021-2022学年六年级数学下册典型例题系列之第三单元：圆柱体积的生活实际问题专项练习（解析版）1．家具厂订购了500根方木，每根方木横截面的面积是0.24m2、长3m，这些木料一共是多少立方米？【解析】0.24×3×500＝0.72×500＝360（立方米）答：这些木料一共是360立方米。

2．用七步洗手法洗手可以有效地清洁双手，预防病毒传播。

小红外出回家用七步洗手法洗一次手，放水时间大约30秒，而自来水管内直径是2厘米，水管内水的流速是每秒8厘米。

小红洗一次手用水多少升？【解析】3.14×（2÷2）²×（30×8）＝3.14×1×240＝753.6（立方厘米）753.6立方厘米＝0.7536升答：小红洗一次手用水0.7536升。

3．有一个圆柱形钢材，它的高是1.5米，底面直径是2米，它的重量是多少吨？（每立方米钢重7.5吨，得数保留整数）【解析】3.14×（2÷2）2×1.5×7.5=3.14×1×1.5×7.5=35.325（吨）≈35(吨)答：它的重量是35吨。

4．一个圆形水池，它的内直径是10米，深2米，池上装有5个同样的进水管，每个管每小时可以注入水7.85立方米，五管齐开几小时可以注满水池？【解析】[3.14×（10÷2）2×2]÷（7.85×5）＝157÷39.25＝4（小时）答：五管齐开4小时可以注满水池。

5．一个圆柱形油桶，底面内直径为40厘米，高50厘米，如果每立方分米柴油重0.85千克，这个油桶可装柴油多少千克？【解析】53.38千克6．一根水管的内直径是4厘米，放水时水的流速是25厘米/秒。

打开水龙头后，往一个容积是94.2升的水桶里放水，放满这桶水需要多少分钟？【解析】3.14×（4÷2）2×25＝3.14×4×25＝314（立方厘米）94.2升＝94200立方厘米94200÷314＝300秒＝5（分钟）答：放满这桶水需要5分钟。

解决问题第1关练速度1.填一填。

（1）求圆柱形水桶能装水多少升，是求它的（）；做一个圆柱形水桶要多少铁皮，是求它的（）。

（2）已知一个正方体、一个长方体与一个圆柱的底面周长相等，高也相等，则它们的体积相比，（）的体积大。

（3）有两个底面积相等的圆柱，一个圆柱的高是6cm，体积是18.84cm³；另一个圆柱的高是10cm，体积是（）cm³。

2.一个圆柱形的玻璃杯，测得底面内直径是8cm，内装药水的深度是16cm，正好占杯内容积的80%，这个玻璃杯的容积是多少毫升？3.如图是一个酸奶瓶，它的瓶身呈圆柱形（不包括瓶颈），底面直径是6cm。

当瓶子正放时瓶内酸奶高为10cm，瓶子倒放时，空余部分高为2cm。

（1）瓶子里酸奶的体积倒置后没变，酸奶的体积加上（）cm高的圆柱的体积就是酸奶瓶的容积。

（2）算一算，酸奶瓶的容积是多少毫升？4.一个水龙头的内直径是1.4cm，打开水龙头后水的流速是25cm/s。

淘气洗手后没有关闭水龙头，10分钟后被发现并关闭，淘气浪费了多少水？第2关练准确率5.输液100m，每分钟输2.5mL，如图是刚过12分钟时吊瓶的数据，求整个吊瓶的容积是多少毫升。

6.把一个底面半径为5cm的圆柱形铁块放入个底面半径为10cm，高为14cm的圆柱形容器里，完全浸没在水中，水面上升了3cm，求这个圆柱形铁块的体积。

7.一支牙膏出口处直径是5mm，小红每次刷牙都挤出1cm长的牙膏。

这支牙膏可用36次。

现将出口处的直径改为6mm，小红还是按习惯每次挤出1cm长的牙膏。

这样这支牙膏能用几次？8下面三个图形的面积都是16cm²（图中的单位：cm）。

用这些图形分别卷成圆柱（图形的宽作为圆柱的高），可以卷成体积最小的圆柱的图形是（），可以卷成体积最大的圆柱的图形是（）。

9.有甲、乙两个圆柱形容器，从里面量得它们的底面半径分别为10cm和5cm，两个容器内分别盛有深10cm和15cm的水，现将乙容器中的一部分水倒入甲容器内，使得两个容器里的水面相平，这时水深多少厘米？第3关练思维10.如图，有一个高为8cm、容积为50mL的圆柱形容器A，里面装满了水。

新人教版小学六年级下数学《用圆柱的体积解决问题》教课方案优秀教课方案《用圆柱的体积解决问题》设计浙江省诸暨市暨阳小学章梧飞一、教课目的（一）知识与技术用已学的圆柱体积知识解决生活中的实质问题，并浸透转变。

（二）过程与方法经历研究不规则物体体积的转变、丈量和计算过程，让学生在着手操作中初步成立“转变”的数学思想，体验“等积变形”的转变过程。

（三）感情态度和价值观经过实践，让学生在合作中成立协作精神，并加强学生“用数学” 的意识。

二、教课重难点教课要点：利用所学知识合理灵巧地剖析、解决不规则物体的体积的计算方法。

教课难点：转变前后的交流。

三、教课准备每组一个矿泉水瓶（课前一致收集农民山泉矿泉水瓶，装有适当清水，水高度分别为 6、7、8、9 厘米），直尺。

四、教课过程（一）复习旧知，做好铺垫1．板书：圆柱的体积。

问：圆柱的体积怎么计算？体积和容积有什么差别？2．揭题：这节课，我们要依据这些体积和容积的知识来解决生活中的实质问题。

（完好板书：用圆柱的体积解决问题。

）【设计企图】经过复习圆柱的体积计算方法以及体积和容积之间的联系和差别，为学习新知做好知识上的准备。

（二）研究实践，体验转变过程1．创建情境，提出问题。

每个小组桌子上有一个没有装满水的矿泉水瓶。

教师：本来这是一瓶装满水的矿泉水，已经喝了一部分，你能依据它来提一个数学识题吗？（随机板书）预设 1：瓶子还有多少水？（剩下多少水？）预设 2：喝了多少水？（也就是瓶子的空气部分。

）预设 3：这个瓶子一共能装多少水？（也就是这个瓶子的容积是多少？）2．你感觉你能轻松解决什么问题？（ 1）预设 1：瓶子有多少水？（怎么解决？）学生：瓶子里剩下的水呈圆柱状，只需量出这个圆柱的底面直径和高就能算出它的体积。

教师：需要用到什么工具？（直尺）你想利用直尺获得哪些数据？（底面直径、水的高度）小结：知道了底面直径和水的高度，要解决这个问题确实易如反掌。

请你准备好直尺，也许等会儿实用哦！（2）预设 2：喝了多少水？学生：喝掉部分的形状是不规则，没有方法计算。

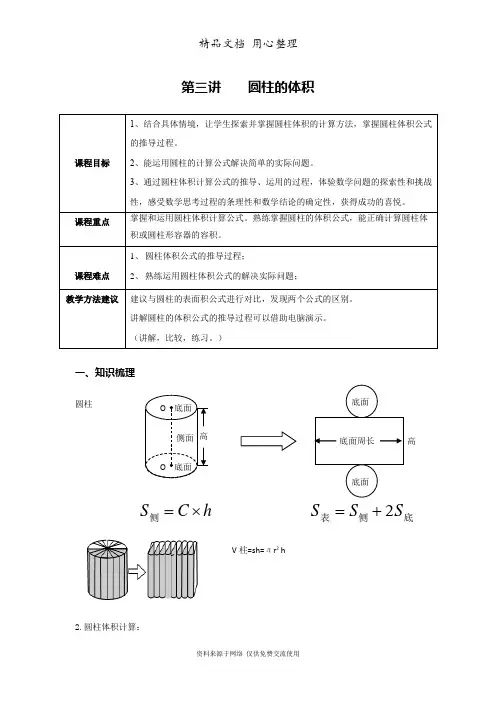
第三讲 圆柱的体积一、知识梳理圆柱V 柱=sh=лr ²h2.圆柱体积计算：hC S ⨯=侧底侧表S S S 2+=高圆柱所占空间的大小是圆柱的体积：圆柱的体积（容积） = 底面积×高，用含有字母的式子表示是：V = sh 或者V = лr²h 。

二、方法归纳1、掌握圆柱的特点，认识它的底面和高，把圆柱转化为长方体，推导出计算公式。

2、理解和掌握求圆柱体积的计算公式，运用公式计算它的体积、容积，并能解决有关的实际问题。

3、观察、比较、实验、猜想、证明等数学活动，增强对空间的认识，建立初步的空间观念，发展应用意识。

三、课堂精讲（一）直接运用圆柱的体积公式例1 一个圆柱体的底面半径是4厘米，高8厘米，求它的表面积和体积．例2 一根圆柱形钢材高2米，其底面周长为12.56分米，它的体积是多少立方分米？【规律方法】会使用圆柱体积计算公式是一个基本的要求。

但知道圆柱体积计算公式的推导过程也非常重要。

体积计算公式的推导过程和之前的圆柱的侧面积计算公式推导过程一样，都用了转化的数学思想。

题中各量计量单位统一是本题的易错点。

【变式训练1】【难度分级】 A1、求下面各圆柱的体积。

（1）底面积0.6平方米，高0.5米（2）底面半径是3厘米，高是5厘米。

（3）底面直径是8米，高是10米。

（4）底面周长是25.12分米，高是2分米。

2、一个圆柱，底面周长18.84分米，高20厘米。

求它的体积？（二）逆用圆柱的体积公式例3一个圆柱体的体积是10立方分米，底面积是2.5平方分米，它的高是多少分米？【规律方法】熟知圆柱体积计算公式，并会把体积公式进行变形使用。

（三）运用圆柱的体积公式解决实际问题例4 一个圆柱形的粮囤，从里面量得底面周长是9.42米，高是2米，每立方米稻谷约重545千克，这个粮囤约装稻谷多少千克？（得数保留整千克数）。

【规律方法】理解求容积的方法和求体积的方法相同，但并不意味着体积就是容积。

《圆柱的体积解决问题》教学设计土地堂小学陈明华教学目标：知识与技能：在自主探究圆柱体容积的过程中，能熟练运用圆柱的体积计算公式解决实际问题。

过程与方法：通过经历发现与提出问题、分析与解决问题和回顾与反思的过程，掌握问题解决的策略，培养学生的应用意识。

情感与态度及价值观：在解决问题的过程中体会转化、推理方法，渗透等积变形的思想，提高学生的学习兴趣，树立学好数学的信心。

学情分析：大多数学生对于圆柱体积的计算方法掌握得比较好，但少数学生在解决问题的时候缺乏灵活性，部分学生动手的能力比较差。

从上次课堂作业中体现出个别学生连圆（圆柱底面）的面积都不会计算，所以对于这样的学生学起来肯定有难度。

教学重点：正确、灵活地运用圆柱体积的计算方法解决实际问题，培养学生的问题意识，体会数学中的转化思想。

教学难点：通过实践操作和合作交流，渗透转化的数学思想。

教学活动：准备一个矿泉水瓶、直尺等，装小半瓶水后，小组合作进行倒置，观察、讨论，得出结论：瓶子里的水倒置后，体积没有变化，水的体积加上18㎝高圆柱的体积就是瓶子的容积。

也就是把瓶子的容积转化成了两个圆柱的体积。

教学过程：一、导入新课我们在五年级学过运用排水法计算不规则物体体积的方法，今天我们来学习一种新的计算不规则物体容积的方法。

教师拿出一个装了半瓶水的瓶子，上下倒转，让学生观察里面水的变化。

思考如何计算出这个瓶子的容积。

【编排意图】教材例7呈现的是一个装了小半瓶水的矿泉水瓶，下部是圆柱形，而上部是一个不规则的立体图形。

教材给出了瓶子平置时的水的高度，要求这个瓶子的容积。

因为这样的问题不是学生常见的常规问题，所以教师为了使学生有所了解才设置了这个演示，让学生能比较容易的发现问题和提出问题的解决方法。

二、合作探究出示教材第27页例7.1.阅读与理解。

学生读题，了解题意。

请学生自己阅读题目，找出题目中的信息和问题。

指名汇报，说出题目中的信息和问题：一个内直径是8㎝的瓶子里，水的高度是7㎝，把瓶盖拧紧倒置放平，无水部分是圆柱形，高度是18㎝.这个瓶子的容积是多少？指导学生根据问题重新梳理信息，找出解决这个问题可能用到的信息，并加以整理。

第五课时《解决问题》教学内容：教科书第27页例7和相关的内容。

教学目标：1．使学生熟练运用圆柱的体积计算公式解决实际问题。

2．使学生通过经历发现和提出问题、分析和解决问题的完整过程，掌握问题解决的策略，培养应用意识。

3．使学生在解决问题的过程中体会转化、推理和变中有不变的数学思想。

教学重点：培养问题意识，体会转化思想。

教学难点：通过实践操作、合作交流，体会转化的数学思想。

（一）导入师：这单元我们学习了哪些圆柱的知识？学生汇报。

今天我们继续学习有关圆柱的知识，解决问题。

（板书课题：解决问题）（二）利用转化的方法，计算瓶子的容积1、出示一个瓶子：看老师这有一个瓶子，给你们变个魔术，把瓶子倒置过来，学生仔细观察，再来一遍，你们有什么发现？学生汇报。

师：瓶子里水的体积在倒置前后有没有变？师：倒置前后，不仅瓶子里水的体积没变，瓶子里空气的体积也没有变。

这样，相当于把不规则的图形转化成一个规则图形。

小结：这是转化思想。

板书：转化那我们看看这道题会做吗：出示例7：一个内直径是8cm的瓶子里，水的高度是7cm，把瓶盖拧紧倒置放平，无水部分是圆柱形，高度是18cm。

这个瓶子的容积是多少？师：请同学们自己阅读题目，找出题目中的信息和问题。

学生汇报，说出信息和问题：一个内直径是8cm 的瓶子里，水的高度是7cm ，把瓶盖拧紧倒置放平，无水部分的高度是18cm 。

这个瓶子的容积是多少？师：根据问题再次梳理信息，找出解决这个问题可能用到的信息，并加以整理。

说说你是怎样理解的。

学生说自己对题意的理解，教师结合实物加以解释：瓶子的内直径是8cm ，水的高度是7cm ，倒置后无水部分高18cm 。

求的是整个瓶子的容积。

2．分析与解答。

师：这个瓶子不是一个完整的圆柱，你有什么想法？学生可能提出转化为学过的图形——圆柱。

教师引导学生思考：应该怎样转化？学生各抒己见，分享自己的设想和操作方法。

教师提供准备好的教具让学生在解释的时候同步演示。