当前位置：文档之家 › 中职升高职数学专题复习——解三角形课件

中职升高职数学专题复习——解三角形课件

  • 格式：ppt
  • 大小：214.00 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

解三角形课件PPT

解三角形课件PPT
所以A=B=C，
所以△ABC是等边三角形.
利用正弦定理证明等式 பைடு நூலகம்名师指津】利用正弦定理证明等式应注意：
观察等式的特点，有边有角，需把边、角统一，为此用 正弦定理将a、b、c转化为sinA、sinB、sinC，此时题目完全 转化成三角函数的运算了.可见，三角形中的三角函数问题也 是解三角形过程中经常遇到的. 【特别提醒】要注意灵活应用正弦定理的变形公式.
∵0°<A<180°，∴A＝60°，∴C＝75°.
当c＝
6－ 2
2时，由余弦定理得
cos A＝b2＋2cb2c－a2＝2＋ 2×
6－ 2
2×
62－2－23＝－12. 2
∵0°<A<180°，∴A＝120°，C＝15°.
故c＝
6＋ 2
2 时，A＝60°，C＝75°或c＝
6－ 2
2 时，A＝
120°，C＝15°.
3.在△ABC中，若B=2A，a∶b 1∶ 3，则A=_______.
【解析】∵ a∶b 1∶ 3,sin A∶sin B 1∶ 3，
即sin A∶sin 2A 1∶ 3,所故以Aco=s3A0°. 3，
2
答案：30°
4.在△ABC中，A=30°，C=45°，c 2，则边a=______.
【解析】在△ABC中，由正弦定理 a 得c ,
sin A sin C a csin A 2 sin 30 1.
sin C sin 45
答案：1
5.在△ABC中，B＝135°，C＝15°，a＝5，则此三角形的
最大边长为多少？
【解析】根据三角形中“大角对大边”可知，此三角形的
最大边为b，
由B＝135°，C＝15°，可得A=30°，

高中数学课件《三角公式》中职总复习

高中数学课件《三角公式》中职总复习

（1）sin αcos α；
（2）s2insinα－α－2ccoossαα.
【解析】（1）解法一：由已知可得方程组
得sin α=3cos α，cos2α=110. 故sin αcos α=3cos αcos α=3cos2α=130.
典例解析
解法二：sin αcos α=ssinin2αα+ccoossα2α=tatna2nαα+1=323+1=130. 解法三：因为tan α=3，所以sin α=3cos α. 所以sin αcos α=ssinin2αα+ccoossα2α=9co3s2cαo+s2cαos2α=9+31=130. （2）因为tan α=csoins αα=3，所以sin α=3cos α. 所以2sisninαα－－2ccooss αα=36ccoossαα－－2ccoossαα=5.
又因为α∈(π2,π)，所以cos α=- 23.
典例解析
【例2】已知α∈(π2,π)，sinα2+cosα2= 26.
（2）因为-
π 2
<α-β<
π 2
，cos(α-β)=
1−sin2(α−β)= 45,
所以cos β=cos［α-(α-β)］=cos αcos(α-β)+sin αsin(α-β)
典例解析
【例2】已知α∈(π2,π)，sinα2+cosα2= 26.
（1）求cos α的值；
（2）若sin(α-β)=-35，β∈(π2,π)，求cos β的值.
【解析】（1）因为（sinα2+cos
α 2
）2=1+2sin
α 2
cos
α 2

解三角形复习课课件

解三角形复习课课件
2. 已知一个三角形的两边长分别为a和b，它们的 02 夹角为θ，且满足a>b，求证：
cosθ=(a²+b²)/(2ab)。
3. 已知一个三角形的三条边长分别为a、b和c， 03 且满足a²=b²+c²，求证：该三角形为直角三角形
。
THANKS
感谢观看
详细描述
三角形的分类是根据其角度和边长进行的，常见的分类包括锐角三角形、直角三 角形、钝角三角形、等边三角形和等腰三角形等。这些分类在解三角形的过程中 具有重要的应用价值，可以帮助我们更好地理解和解决问题。
02
解三角形的主要方法
正弦定理
总结词
利用正弦定理可以解决与三角形边和角 有关的问题，特别是当已知两边及其夹 角时。
解三角形时常见的错误
忽视角度范围
在解题过程中，由于忽视角度的范围 ，导致得出的答案不符合实际情况。
使用错误的公式
在解题过程中，使用了不合适的三角 恒等式或解三角形公式，导致答案错
误。
混淆相似与全等三角形
在解题过程中，将相似与全等三角形 混淆，导致解题思路和答案错误。
计算错误
由于计算失误，导致得出的答案与正 确答案不符。
几何图形制作中的应用
01
制作几何图形
通过解三角形的方法，可以制作各种几何图形， 如三角形、四边形等。
02
制作立体几何模型
通过解三角形的方法，可以制作各种立体几何模 型，如立方体、球体等。
建筑设计中的应用
设计建筑结构
通过解三角形的方法，可以设计出建筑的支撑结 构，以确保建筑的稳定性。
设计建筑外观
通过解三角形的方法，可以设计出建筑的外观线 条和造型，以达到美观和实用的效果。
解三角形复习课课件

中职数学6.4解三角形课件

中职数学6.4解三角形课件

容易看出，利用正弦定理可以解决下列两类问题： (1) 已知三角形的两边和其中一边所对的角,求其他两角和另一条边； (2) 已知三角形的两个角和任意一边,求其他两边和另一个角.
6.4.2 正弦定理
情境导入 探索新知 典型例题 巩固练习 归纳总结 布置作业
例3 在ΔABC中, ∠B=45°，∠C=15°，a=5，求b. 解
6.4 解三角形
6.4 解三角形
ΔABC中,常用∠A、∠B、∠C 表示 三个角，用 a、b、c分别表示这三个角的 对边．根据已知条件求三角形的边和角的 过程称为解三角形.
在生产实践和科学研究中,经常会遇到解三角形的 问题．余弦定理和正弦定理反映了任意三角形中边和 角之间的数量关系，是解三角形的重要工具.
6.4.1 三角形面积公式
情境导入 探索新知 典型例题 巩固练习 归纳总结 布置作业
用ΔABC表示所建花圃，其中， b=4, c=6. 以ΔABC的顶点A为坐标原点， 建立如图所示的平面直角坐标系.于是, 点A的坐标为(0,0)，点B的坐标为(c,0).
设点C的坐标为(x0,y0)，过点C作AB边上的高CD，则CD⊥AB， 且 =CD.
6.4.1 三角形面积公式
情境导入 探索新知 典型例题 巩固练习 归纳总结 布置作业
由三角函数的定义，可以得到
同理可得， 因此，
6.4.1 三角形面积公式
情境导入 探索新知 典型例题 巩固练习 归纳总结 布置作业
这就是说，三角形的面积等于它的任意两 边及其夹角的正弦乘积的一半.
6.4.1 三角形面积公式
6.4.3
余弦定理
6.4.3 余弦定理
情境导入 探索新知 典型例题 巩固练习 归纳总结 布置作业
在6.4.1的“情境与问题” 中，园林工人在修建花圃的过 程中,需在墙角的对面建造一道 篱笆墙，问所建篱笆墙的长度 为多少(不考虑其他因素)？

考点35 正、余弦定理与解三角形课件-2021年浙江省中职升学数学一轮复习

考点35 正、余弦定理与解三角形课件-2021年浙江省中职升学数学一轮复习

c2=___a_2_+_b_2－__2_a_b_c_o_s_C_.
b2 c2 a2
a2 c2 b2
变式：cosA=______2_b_c______，cosB=______2_a_c______，
a2 b2 c2
cosC=______2_a_b______.
知识要点
6.利用余弦定理主要解哪两类解三角形问题： （1）_已__知__三__角__形__两__边__及__夹__角__，__可__求__出__第__三__边________________； （2）_已__知__三__角__形__两__边__及__其__一__边__对__角__，__可__求__其__他__的__角__和__第__三__边__.
典例剖析
【变式训练4】 在△ABC中，已知S△ABC＝6 3，∠A＝60°， b＋c＝10，求a的值．
解∴：12 ∵bcsSi△n6AB0C°＝＝12 6bcs3in，A即＝b6c＝3 2，4.
联立
bc 24, b c 10,
解得
b c
6, 4
或
b c
4, 6.
在△ABC中，由余弦定理得a2＝b2＋c2－2bccosA＝62＋42－
∴sinC＝ BA sin B 2 sin 60 =1.
AC
3
【思路点拨】 用余弦定理来解已知三边之比的问题较为常见， 通常采用设出三边的长，再用余弦定理来解决.
知识要点
考点35 正、余弦定理与解三角形
1.基本概念：由三角形六个元素（三条边和三个角）中的三
个已知元素（至少有一个元素是边），求其余三个未知元素
的过程叫做__解__三__角__形____.
2.正弦定理：在一个三角形中，各边和它所对的角的_正__弦___

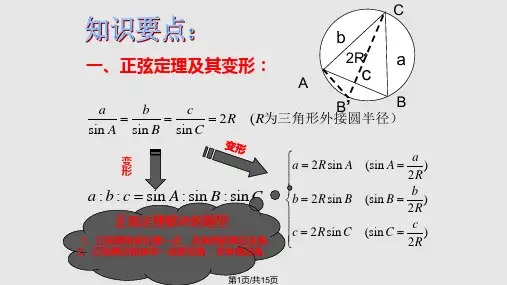
解三角形章节复习课PPT课件

解三角形章节复习课PPT课件

A
b
ha
aC
第2页/共15页
四、解三角形的思路
• 1、根据题意，画出图形，作出标识。 • 2、由已知条件和欲求的量确定可解的三角形和要解的三角形。并找出其中
的联系。 • 3、若题中无直接可解的三角形应考虑用方程的思想来解题。（在列方程的
过程中，可以以公共边，互补，互余的俩角等做等量关系）
第3页/共15页
C
b
一、正弦定理及其变形：
A
2R a
c
a b c 2R (R为三角形外接B’圆半径）B
sin A sin B sin C
变 形
a : b : c sin A : sin B : sin C
正弦定理解决的题型：
1、已知两角和任意一边，求其他的两边及角. 2、已知两边和其中一边的对角，求其他边角.
2
(1) cos C 1 8
（2）c=6
第10页/共15页
11. 在ABC中，已知A、B、C所对的边分别是a、b、c，边c 7， 2
且 tan A tan B 3 tan A• tan B 3，又ABC的面积为
SABC
3 3 ，求a 2
b的值.
解：由已知tan A tan B 3(tan A• tan B 1)
变、 某舰艇在A处测得遇险渔船在北偏东45距离10海里的C处， 此时得 知， 该渔船沿北偏东105方向， 以每小时9海里的速度向一小岛靠近， 舰艇时速21海里， 则舰艇到达渔船的最短时间是_______
小结：准确的将实际问题的条件画出三角形，转化为 解三角形问题，是关键。
第7页/共15页
练习 一、选择题：
1、在ＡＢＣ中，AC= 3,A 45 ,C 75 ,则BC

2024版中职数学全套PPT课件完整版

2024版中职数学全套PPT课件完整版
数学归纳法应用
数学归纳法在数列求和、不等式证明、组合数学等领域 有广泛应用。例如，可以利用数学归纳法证明等差数列 和等比数列的求和公式。
04
平面解析几何初步
直线方程求解技巧
熟练掌握直线方程的基本 形式：一般式、点斜式、 斜截式等，理解各参数的 含义。
掌握直线方程的求解方法： 如两点式、截距式等，能 根据已知条件选择合适的 求解方法。
根据数据分析结果，对实际问题作出解释和判断，为决策提供依据。
THANKS
感谢观看
多面体的性质
了解多面体的性质，如欧拉公式等，能够运用性质解决相关问题。
空间向量基本概念运算
空间向量的定义与表示 理解空间向量的定义和表示方法，能够正确表示空间向量。
空间向量的线性运算 掌握空间向量的加法、减法、数乘等线性运算规则，能够 运用规则进行运算。
空间向量的坐标运算 理解空间向量的坐标概念，能够运用坐标进行向量的运算。
应的弧长为单位。两者之间可以通过公式进行相互转换。
角度制与弧度制下的三角函数值
02
在不同的角度制或弧度制下，三角函数的值也会有所不同，需
要注意转换。
实际应用中的转换问题
03
在实际应用中，如物理、工程等领域，经常需要进行角度制与
弧度制的转换，需要熟练掌握转换方法。
三角函数基本概念及性质
1 2
三角函数定义及符号 正弦、余弦、正切等三角函数的定义及符号，以 及各象限内三角函数的正负性。
数列。
求和公式推导
利用错位相减法或无穷递缩等比 数列法，可推导出等比数列的求
和公式。
求和公式应用
利用求和公式，可以快速求解等 比数列的前n项和。
数学归纳法原理及应用
数学归纳法原理

解三角形课件

解三角形课件

（3）a 18, b 20, A 150
解法一：（几何作图法）分别如下图①、②、③
c
C
b=22
A
B
DA
a=11 B
c
b=20 A
解法二：(1)2 2 2 3 2 6 ABC有两解 2
(2)11 22 1 AB解C三有角形一课件解! (3)A 150 ABC无解 2
例5. ABC中，已知A 60,b 4 3,为使此三角形只有
2sin B sinC 1 - cos（B C） ①
又cos(B C ) cos B cosC sin B sinC ②
由 ① 、 ② 得cos B cosC sin B sinC 1
即cos(B C ) 1 B C ABC是 等 腰 三角 形 解三角形课件!
已知边与角之间的关系
2
则当为多少时OAB的面积最 大值？
解 ：SOBC SOCMD ( SOAC SOBD SABM )
SOCED
1
SOAC
1 cos 2
SOBD
1 2
sin
Y
D(0,1)
O
B(sin ,1) M
A(1,cos ) X
C(1,0)
SABM
1 2
(1
cos
)(1
sin
)
SABM
1（1- sin 2
cos
sin
cos）
SOAC
SOBD SABM
1 1 sin cos 22
SOBC
1 2
(1 sin
cos )
1 2
(1
1 sin2 2
)
当 时 2
S
OBC
达
到

四川省中等职业学校对口升学考试-数学-第五章《三角函数》总复习-课件

四川省中等职业学校对口升学考试-数学-第五章《三角函数》总复习-课件
(4)扇形的弧度与面积公式.
扇形的弧长公式：l=|α|r或l=nπr/180.
扇形的面积公式：S=1/2lr=1/2|α|r2或S=nπr2/360.
(5)象限角和轴线角的表示法.
第一象限角：{α|2kπ＜α＜2kπ+π/2，k∈Z}.
第二象限角：{α|2kπ+π/2＜α＜2kπ+π，k∈Z}.
第三象限角：{α|2kπ+π＜α＜2kπ+3π/2，k∈Z}.
（3）tan(α±β)=tanα±tanβ/(1∓tanα·tanβ).
2.倍角公式
(1)sin2α=2sinαcosα.
(2)cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α.
(3)tan2α=2tanα/(1-tan2α).
一
知识清单
3.降次公式
(1)sin2α=1-cos 2α2;(2)cos2α=1+cos 2α2.
（1）第一象限的诱导公式.
sin(2kπ+α)=sin α,cos(2kπ+α)=cos α,tan(2kπ+α)=tan α.(k∈Z)
（2）第二象限的诱导公式.
sin(π-α)=sin α,cos(π-α)=-cos α,tan(π-α)=-tan α.
（3）第三象限的诱导公式.
sin(π+α)=-sin α,cos(π+α)=-cos α,tan(π+α)=tan α.
相同的角不一定相等，但相等的角终边一定相同.
一
典例解析
例2
将75°转化为弧度为 .
【解析】 由角度与弧度的换算关系可得75°=π/180×75=5/12π.
【技巧点拨】 角度化为弧度,分母是180;弧度化为角度,分母是π.

中职升高职数学专题复习——解三角形课件

中职升高职数学专题复习——解三角形课件

A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
用余弦定 1.应用正、余弦定理解三角形: 理 ①已知三边,求其它;
②已知两边及其夹角,求其它;
用余弦定 理
③已知两边及一边对角,求其它;
正弦定理、余弦定理都可以
④已知一边及两角,求其它;
用正弦定理
△ABC中,B=450,AC=
的形状是（ C ）
b
（1 ,2）
1.会用正余弦定理,结合三角形的性质 解三角形,求解时注意解的情况; 已知两边及一边对角,求其它. 会有二解,一解的情况. 2.会用正余弦定理进行边角互化,关键 是统一.
0
2.四边形ABCD中,AD⊥CD来自AD=10, AB=14,∠BDA=600,∠BCD=1350, 求BD及BC的长。
D
10 600 14
C
A
B
c 1 3.△ABC中, b c a bc, 且 3 b 2 求∠A及tanB的值.
2 2 2
1.△ABC中, 若 ( 3b c ) cos A a cos C , 则cosA= 3 3 2.△ABC中, 若a· cosA=b· cosB,则△ABC A.等腰三角形 B.直角三角形 C.等腰三角形或直角三角形 D.等腰直角三角形 a 的取值范围是： 3.△ABC中, A=2B,则
会用正余弦定理结合三角形的性质解三角形求解时注意解的情况
中职升高职数学专题复习 解三角形
a=2RsinA a b c 1.正弦定理: sinA = sinB= sinC= 2R 2.余弦定理: b2+c2-a2 cosA= 2 2 2 2bc
cosC= 3.面积公式: 2ab 1 absinC= 1 bcsinA= 1 acsinB S= 2 2 2 4.三角形的性质: A+B+C=π 大边对大角,大角对大边

解三角形-PPT课件

解三角形-PPT课件
2023最新整理收集 do something
本 章 优 化 总 结
本章优化总结
知识体系网络
专题探究精讲
知识体系网络
专题探究精讲
判断三角形形状 判断三角形的形状，一般有以下两种途径： (1)将已知条件统一化成边的关系，用代数方法 求解； (2)将已知条件统一化成角的关系，用三角方法 求解． 在解三角形时的常用结论有：
【解】 (1)依题意，PA－PB＝1.5×8＝12 (km)， PC－PB＝1.5×20＝30 (km)． 因此 PB＝(x－12) km，PC＝(18＋x) km. 在△PAB 中，AB＝20 km， cos∠PAB＝PA2＋2PAAB·A2－B PB2＝x2＋2022－x·20x－122 ＝3x＋ 5x32.
(1)设A到P的距离为x km，用x表示B、C到P 的距离，并求x的值； (2)求静止目标P到海防警戒线a的距离．(结果 精确到0.01 km)
【思路点拨】 (1)PA、PB、PC长度之间的关 系可以通过收到信号的先后时间建立起来； (2)作PD⊥a，垂足为D，要求PD的长，只需要 求出PA的长和cos∠APD，即cos∠PAB的 值．由题意，PA－PB，PC－PB都是定值，因 此，只需要分别在△PAB和△PAC中，求出 cos∠PAB，cos∠PAC的表达式，建立方程即可.
例4 如图所示，a是海面上一条南北方向的 海防警戒线，在a上点A处有一个水声监测点, 另两个监测点B、C分别在A的正东方向20 km 处和54 km处，某时刻，监测点B收到发自静 止目标P的一个声波，8 s后监测点A、20 s后 监测点C相继收到这一信号，在当时的气象条 件下，声波在水中的传播速度是1.5 km/s.
(1) 在 △ ABC 中 ， ∠ A> ∠ B⇔ a>b ⇔ sinA>sinB ⇔

中职数学人教版拓展模块第一章三角公式及其应用《三角形的面积及正弦定理(第2课时)》课件

中职数学人教版拓展模块第一章三角公式及其应用《三角形的面积及正弦定理(第2课时)》课件
解: 因为



=
=

，所以



=
°

≈ . ．
用函数型计算器计算可得
∠ ≈ °′或∠ ≈ °′．
但°′+° > °，舍去°′．
所以∠ ≈ °′ ．
温故知新
1. 正弦定理：
2. 正弦定理在解三角形中的应用主要有以下两种情况：

=
2 3sin 45°
2 2
=
3
，
2
所以∠ = 60°或∠ = 120° （如图）．
练习巩固
练习2 在△ 中，已知＝15， = ，∠ = °，
求∠ （角度精确到1分） ．
解: 因为


=
=


，所以


=
°



中职数学人教版拓展模块第一
章三角公式及其应用
1.4.2 三角形的面积及正弦定理
（第2课时）
复习提问
1．写出正弦定理公式，并说说你是怎样把握公式的特征去进行记忆的．
2．应用正弦定理可解怎样条件下的斜三角形．
新知探究
➢ 正弦定理
我们把以上公式称为正弦定理，即在一个三角形中，各边与
它所对角的正弦的比相等．
= ，
用函数型计算器计算可得
∠ ≈ °′或∠ ≈ °′．
所以∠ ≈ °′或∠ ≈ °′．
新知探究
例4 在△中，已知 = ， = ，∠ = °，求∠，
（角度精确到1分）．
解

sin
因为
=
sin =

sin
，所以
sin 6sin 60°

解三角形完整讲义课件.doc

解三角形完整讲义课件.doc

正余弦定理知识要点：a b c1、正弦定理: 2Rsin A sin B sin C或变形： a :b: c sin A:s in B : sin C .2 2 2a b c 2bc cos A2 2 2b ac 2ac cosB2 2 2c b a 2ba cosC 或cos AcosBcosC2 2 2b c a2bc2 2 2a c b2ac2 2 2b a c2ab2、余弦定理：.3、解斜三角形的常规思维方法是：（1）已知两角和一边（如A、B、C），由A+B+C =π求C，由正弦定理求a、b；（2）已知两边和夹角（如a、b、c），应用余弦定理求 c 边；再应用正弦定理先求较短边所对的角，然后利用A+B+C =π，求另一角；（3）已知两边和其中一边的对角（如a、b、A），应用正弦定理求B，由A+B+C = π求C，再由正弦定理或余弦定理求 c 边，要注意解可能有多种情况；（4）已知三边a、b、c，应余弦定理求A、B，再由A+B+C =π，求角C。

4、判定三角形形状时，可利用正余弦定理实现边角转化，统一成边的形式或角的形式.5、解三角形问题可能出现一解、两解或无解的情况，这时应结合“三角形中大边对大角定理及几何作图来帮助理解”。

6、已知三角形两边a,b,这两边夹角C，则S＝1/2 * absinC7、三角学中的射影定理：在△ABC 中，b a cos C c cos A，,8、两内角与其正弦值：在△ABC 中，A B sin A sin B ，,【例题】在锐角三角形ABC中，有（ B ）A．cosA>sinB且cosB>sinA B．cosA<sinB且cosB<sinAC．cosA>sinB 且cosB<sinA D．cosA<sinB 且cosB>sinA9、三角形内切圆的半径：r2Sa b c，特别地，r直a b c斜2正弦定理专题：公式的直接应用1、已知△ABC 中，a 2 ，b 3 ，B 60 ，那么角 A 等于（）A．135 B．90 C．45 D．30 2、在△ABC中，a＝2 3 ，b＝2 2 ，B＝45°，则A 等于（ C ）A．30°B．60°C．60°或120°D．30°或150°3、△ABC 的内角A，B，C 的对边分别为a，b，c，若c2，b 6，B 120，则a1等于（）A．B．2 C．D．6 3 2 4、已知△ABC中，A 30 ，C 105 ，b 8 ，则 a 等于（ B ）A．4 B.4 2 C.4 3 D. 4 5 5、在△ABC中，a＝10，B=60°,C=45°,则c等于（ B ）A．10 3 B．10 3 1 C． 3 1 D．10 36、已知ABC 的内角 A ，B ，C 所对的边分别为a，b ，c，若1s i n A ，b 3sin B ，33则a等于．（）37、△ABC中，B 45 ，C 60 ，c 1，则最短边的边长等于（ A ）A .63B.62C .12D .328、△ABC中，A:B1: 2，C 的平分线CD 把三角形面积分成3: 2 两部分，则cos A （ C ）A . 13B .12C .34D .0cos 2A cos2 B 1 19、在△ABC中，证明： 2 2 2 2a b a b。

高教版中职数学基础模块《余弦定理、正弦定理》总复习课件

高教版中职数学基础模块《余弦定理、正弦定理》总复习课件

(3)△ABC的三边分别为m，n，√m2+mn+n2，求△ABC的最大角；
(4)在△ABC中，b=12,∠A=30°，∠B=120°，求边c.
【举一反三】

1. 在△ABC中，b=2，c= ，∠B= ，求∠C；

2. 在△ABC中，a=32，b=16 ，A=2B，求边c；
3. 在△ABC中，a=5，b=3，a、b两边夹角的余弦是方程5x2-7x-6=0其中一根 , 求边c；
a
b
c
________=________=________=2R
sinA
sinB
sinC
正弦定理的应用：
(1)已知两角和一边，求其他元素；
(2)已知两边和其中一边所对的角，求其他元素.
三、三角形的面积
三角形的面积，等于它的任意两边及其夹角的正弦乘积的一半.
1 bcsinA
1 absinC
1 acsinB
(2)在△ABC中，a=2 ，c= ，∠B=105°，则S△ABC=__________；
一课一案 高效复习
题型3
判断三角形的形状
【例3】 在△ABC中，判断以下情况三角形的形状：
(1)a=10 ，b=5，c=9 ；
(2)sin2A+sin2B=sin2C ；
(3)a:b:c= : : ；


4. 在△ABC中，a=1，c= ，cosC= ，求(1)sin(A+B)的值；(2)b的值.
一课一案 高效复习
题型2
三角形面积公式的应用


【例2】在△ABC中，∠B= ，a= ，b=12，则△ABC的面积是________；
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
0
2.四边形ABCD中,AD⊥CD,AD=10, AB=14,∠BDA=600,∠BCD=1350, 求BD及BC的长。
D
10 600 14
C
A
B
c 1 3.△ABC中, b c a bc, 且 3 b 2 求∠A及tanB的值.
2 2 2
1.△ABC中, 若 ( 3b c ) cos A a cos C , 则cosA= 3 3 2.△ABC中, 若a· cosA=b· cosB,则△ABC A.等腰三角形 B.直角三角形 C.等腰三角形或直角三角形 D.等腰直角三角形 a 的取值范围是： 3.△ABC中, A=2B,则
的形状是（ C ）
b
（1 ,2）
1.会用正余弦定理,结合三角形的性质 解三角形,求解时注意解的情况; 已知两边及一边对角,求其它. 会有二解,一解的情况. 2.会用正余弦定理进行边角互化,关键 是统一.
a =b +c -2bccosA 2+c2-b2 a b2=a2+c2-2accosB cosB= 2ac c2=a2+b2-2abcosC a2+b2-c2
1.△ABC中,sinA:sinB:sinC=3:2:4, 1 则cosC= . 4 2.△ABC中,“A>B”是“sinA>sinB”的 C 条件.
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
用余弦定 1.应用正、余弦定理解三角形 : 理 ①已知三边,求其它;
②已知两边及Hale Waihona Puke 夹角,求其它;用余弦定 理
③已知两边及一边对角,求其它;
正弦定理、余弦定理都可以
④已知一边及两角,求其它;
用正弦定理
△ABC中,B=450,AC=
中职升高职数学专题复习 解三角形
a=2RsinA a b c 1.正弦定理: sinA = sinB= sinC= 2R 2.余弦定理: b2+c2-a2 cosA= 2 2 2 2bc
cosC= 3.面积公式: 2ab 1 1 1 S= 2 absinC= bcsinA= acsinB 2 2 4.三角形的性质: A+B+C=π 大边对大角,大角对大边
(1)求BC的长; (2)设AB中点为D,求中线CD的长.
A D B
5 10 , sin C 5
10
C
△ABC中,角A,B,C所对的边分别为a,b,c,
5 若 cos ( A ) cos A , b c 3a 2 4
2
求角A,B,C.
1. △ABC中, a 3 , b 2 , B 45 , 求∠A;