三星堆出土的1号青铜神树上,为何只有九只鸟,第十只去哪了
- 格式:docx
- 大小:2.54 MB
- 文档页数:6

三星堆新发现通天的神树文/邹鹏 图/唐二胖胖在三星堆博物馆一号展馆的展厅里有一件极其珍贵的青铜器,所有人在看到它的第一眼时都会不由自主地发出惊叹。
它形体庞大、结构复杂、造型精美,是3000多年前三星堆古人创作的一件绝世精品,它就是被称为三星堆博物馆“镇馆之宝”的青铜神树。
现在就让我们一起走近这件文物,了解它和它背后的故事。
从“2000”到“1”的重获新生1986年,考古人员在三星堆的二号“祭祀坑”里发现了一些奇奇怪怪的青铜器残件和碎片。
它们有的像弯曲的树枝,有的像树叶,有的像花和果实,还有一些是造型精美的青铜鸟。
考古人员经过清点发现,这些青铜器的残件和碎片竟然有2000多件。
最让考古人员和文物修复人员感到惊喜的是,这些残件和碎片都是可以拼接、修复的。
经过文物修复人员近10年的努力,2000多件残件和碎片被拼接起来修复好了,一件残高达到3.96米的青铜器重获新生,出现在人们眼前,它看起来像是一棵高大的树。
它不仅是中国目前发现的3000多年前的青铜器中形体最大的,也是世界上发现的同时代单件青铜器中形体最大的。
因此,它有了一个霸气的名字——青铜神树。
青铜神树上有什么这么高大的青铜器上都有些什么呢?让我们一起来看看吧!神树的最下面是一个巨大的圆形底座,底座三面镂空,装饰有精美的太阳纹和云气纹。
青铜神树修复现场这个底座似乎是一座神山的象征,而高大挺拔的青铜树则是矗立在神山上的神树。
目光上移,你会看到神树被分为三层,每一层都有三根弯曲的树枝,每根树枝又分成了两根或三根果枝,其中一根向上,每根果枝上都长着镂空的叶子和像桃子那样大的果实,其中朝上的果实上还站立着鸟,一共有9只。
最引人注目的是树上这9只造型相同的鸟,它们都长着大大的嘴、弯弯的喙,身体镂空,尾羽上翘,造型栩栩如生。
虽然大部分鸟的翅膀已经残缺不全,但我们依旧能据此想象它们展翅欲飞的样子。
还有让人意想不到的设计呢,神树的一侧有一条造型独特的龙。
仔细观察你会发现,这条龙是头朝下、尾朝上倒挂在树上的。

三星堆十大未解之谜作者:来源:《家教世界·创新阅读》2021年第06期自1934年開始大规模挖掘以来,三星堆拢共被发掘面积不到2万平方米,而其遗址总占地面积却高达12平方公里!也就是说,我们几十年的考古工作才仅仅揭开了它神秘面纱的千分之二。
2021年,国家重启三星堆神秘之旅,发现了很多新的“猛料”,造型奇特的珍稀国宝接二连三地浮现。
而三星堆之所以如此神秘,就在于它完全独立于中原文明的特殊风格,乃至留下了“十大未解之谜”。
起源之谜三星堆的太阳轮、金权杖、怪异的人物特征等,都与古埃及、苏美尔甚至玛雅文明有相似之处,三星堆文明和他们有关吗?有人支持外星说:文明高度发达,不留任何记载,风格特立独行,只有外星人才能这样;但更多的专家认为:三星堆文明是中华文明起源的重要组成部分,绝对不会是外星人的产物。
至于青铜器面具,可能是因为古代人比较信奉神,所以用想象中“神”的模样建造。
三星堆文明一定是属于我们中华文明的一部分,是我们中华文明多元一体的表现。
消失之谜三星堆占地面积广、青铜文化发达、建设规模庞大,为什么会突然消失,而且没有留下子脉呢?学者总结了以下几大推测:外族入侵,洪水灾害,部落迁移,内部矛盾……可不管是哪种,三星堆人总会有所遗存的吧?那么,这些后裔又去哪儿了?文字之谜三星堆存在时间跨度非常大,约距今5000年至3200年,试问一个发展了近两千年的文明,怎么会不形成文字?他们用什么交流,手语吗?而且,根据出土文物显示,三星堆应该与商朝有过文化交流,殷商有甲骨文,而三星堆却没有,这很不科学,毕竟二者是同时代、同发达的两大文明。
金杖之谜提起权杖,我们会不由自主联想到古埃及法老手中的东西,好像这类象征权力的物件非常地具有西方风格,而“鼎”似乎才是中国历史特色。
但有学者认为,中国高古时期也有使用权杖的习惯,三星堆的这根金权杖,终究还是未解之谜。
象牙之谜新近发现的祭祀坑中出土了大量象牙,那么这些象牙的来源是哪里呢?专家分为“土著象牙”与“外来象牙”两支观点队伍。

三星堆文明(古蜀文化遗址)三星堆遗址是一处距今4800年至3100年左右(公元前2800年至公元前1100年)的古蜀文化遗址,面积达12平方公里,是中国20世纪重大的考古发现之一。
自20世纪20年代以来,中外考古学家进行了大量的考古发掘和专题研究,发现了城墙遗址和大量精美的文物。
三星堆遗址和文物的发现有力地证明了三四千年前古蜀国的存在和中华文明起源的多样性。
1988年1月,被国务院公布为全国重点文物保护单位。
三星堆位置位于四川省广汉市遗址种类三星堆文明三星堆遗址内存在三种面貌不同但又连续发展的三期考古学文化,即以成都平原龙山时代至夏代遗址群为代表的一期文化,又称“宝墩文化”;以商代三星堆规模宏大的古城和高度发达的青铜文明为代表的二期文化;以商末至西周早期三星堆废弃古城时期为代表的三期文化,即成都“十二桥文化”。
在三星堆二期文化中,青铜文明的自身文化特点始终占据主导地位,并且其影响范围也超出了传统的古蜀国分布的成都平原,扩散到陕南地区和江汉平原等地。
同时,青铜文明也受到了中原夏商文明及长江中游地区、陕南地区文明的强烈影响,表现出古蜀文明强烈的内聚和外衍的两面性。
三星堆遗址及其出土文物有许许多多的神秘之处,世界各国的考古专家争论了半个多世纪,仍有许多千古之谜至今难以破译,以致不少外国媒体称三星堆遗址是来自“外星人”的文化。
[2]出土文物三星堆出土的大量珍贵文物。
其中最神奇的便是众多青铜造像,这些青铜像铸造精美、形态各异,在众多的青铜人面像里有三件著名的“千里眼、顺风耳”造型,它们不仅体型庞大,而且眼球明显突出眼眶,双耳更是极尽夸张,长大似兽耳,大嘴亦阔至耳根,它们有的唇吻三重嘴角上翘的微笑状。
其中最大的一件通高65厘米、宽138厘米,圆柱形眼珠突出眼眶达16.5厘米。
另一件鼻梁上方镶嵌有高达66厘米的装饰物,既像通天的卷云纹,又像长有羽饰翘尾卷角势欲腾飞的夔龙状。
在世界所有考古发现中,三星堆遗址出土的青铜神树,称得上是一件绝无仅有极其奇妙的器物。

三星堆通天神树1(1196)各位游客朋友,大家好!今天我带领大家参观三星堆博物馆,三星堆博物馆位于四川广汉南兴镇,距广汉城区五公里。
我们的游览路线是序厅、一至六展厅。
参观时请大家注意安全,带好随身物品。
咱们三星堆博物馆于1992年8月奠基,1997年10月正式开放。
大家有没有想过她的名字是怎么来的呢?有人说,她是玉皇大帝从天上撒下的三堆土,也有人认为它是天上掉下的三颗星星。
她真的像传说的这样这么神秘吗?事实上,他是四川地区、目前所知、范围最大、延续时间最长,文化内涵最丰富的古城、古国、古蜀文化遗址,被誉为“世界第九大奇观”。
就连当代学者余秋雨先生也说:中国的历史过于清晰,缺乏神秘感,索性我们还有三星堆。
咱们现在所处的位置就是三星堆博物馆的综合馆,此馆为基础陈列馆,由《三星伴月》和《三星永耀》组成。
前者陈列金、铜、玉石、陶等各类文物,全面系统的介绍古蜀国在各个领域取得的辉煌成就。
后者系统展示三星堆造型神秘诡谲的青铜神品。
好了,游客朋友们,现在映入我们眼帘的这棵通天神树,那可是三星堆文物中最具神韵的重器神树,更是综合馆的压轴戏。
对于神树而言,想必大家都知道,北欧神话的宇宙树,古埃及的天树,西印度的宇宙树,他们都体现了古人精神的追求、信仰和崇拜,但都限于图腾崇拜,唯有咱们古蜀人把它造成一个青铜实物。
她通高3.95m,重达500多公斤,是全世界体积最大的青铜制品。
由底座,树,及龙三部分组成。
底座呈穹窿形,象征着一座神山。
古人认为山是离天最近的地方,在神山上矗立一棵能到达天堂的神树,无疑象征了神树具有通天的功能。
树分三层,每层三支,共九支,每个枝头都有一只鸟儿,共有九只鸟,由于树的顶部残缺,现已无法考证是否还有第十只鸟儿咯!鸟啊,在上古时候鸟是太阳的象征,相信大家都知道“金乌西坠,玉兔东升”这个成语是吧!直至今日我们仍然以“金乌”来称呼太阳。
所以神树上的鸟代表的是太阳。
这样看来,这棵树似乎还影射了著名的神话传说“后羿射日”。


三星堆青铜神树——生命之树三星堆遗址发掘现场超出所有人的预料,看情形,似乎三千年前这里的一切都被砸烂烧毁过,仿佛已经完成了一场涅槃。
二号祭祀坑出土了几百块青铜碎片,这些留在人间的片段,还能拼贴出那个世界的一丝端倪吗?三星堆文物修复团队历经八年,拼接出三千年前这里最大最完整的一件,当它呈现之时,新的谜团又接踵而至。
器物所要表达的意图完全超出人们的经验。
眼前这件青铜器残高3.96米,由基座和主体两部分组成。
树顶已残缺,基座仿佛三座山相连,主干三层,于山顶节节攀升,人们很容易联想它是一棵大树。
树的树枝分为三层,每层三枝,树枝上分别有两条果枝,一条向上,一条下垂,果托硕大,全树共有九只鸟,站立在向上果枝的果实上。
再仔细观察,我们可以看到它的非凡。
一条龙沿主干旁侧而下,蓄势待飞,不难想像,它凌空飞舞的壮阔景象!这棵树似乎并非生长于人间,也不仅仅是古蜀先民对自然的理解,不只是他们对鸟类划过天际和在树上栖息的观察。
几棵树也许象征着九天,树顶是否已经是九天之外?神树所蕴含的秘密可能还不止这些,从另一株至今只修复出下半段的青铜神树底座,能看到更多隐喻和象征。
它的三面各有一跪坐铜人像,前臂残缺,参照出土的其他青铜人物来推测,很可能是双臂前伸手持礼器如璋、琮等,表现祭祀仪式的情境。
三星堆出土的其它青铜器,同样证实了古蜀先民非凡的创造力。
不断试图沟通天地,认识宇宙的可能。
这些符号与青铜神树一样,也许都来自一场仪式。
这些,也许超越了他们日常可见的形象,成为符号,成为拥有去过另一个维度和时空的神秘力量。
在全世界各大文明的神话中,大树都是天地之间的灵物。
历史,文明,想像似乎都是以一种相同的方式构建起来的,这种连接方式就如同树状结构。
树立天地。
生命之树成为人类一个古老的象征。



专题11.1 两个计数原理1.(2021·全国·高二单元测试)青铜神树是四川省广汉市三星堆遗址出土的文物,共有八棵,其中一号神树有三层枝叶,每层有三根树枝,树枝上分别有两条果枝,一条上翘、一条下垂,每层上翘的果枝上都站立着一只鸟,鸟共九只(即太阳神鸟).现从中任选三只神鸟,则三只神鸟来自不同层枝叶的选法种数为( )A .6B .18C .27D .36【答案】C【分析】按照分步乘法计数原理从每层枝叶各选一只神鸟即可得到答案.【详解】每只神鸟有3种选法,三只神鸟来自不同层枝叶的选法种数有33327⨯⨯=(种).故选:C.2.(2021·全国·高二课时练习)中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)中的一种,现有十二生肖的吉祥物各一个,甲同学喜欢牛和马,乙同学喜欢牛、狗和羊,丙同学哪个吉祥物都喜欢,三位同学按甲、乙、丙的顺序依次选一个作为礼物,如果让三位同学选取的礼物都满意,那么不同的选法有()A .360种B .50种C .60种D .90种【答案】B【分析】首先根据题意分成第一类甲同学选择牛和第二类甲同学选择马,分别计算各类的选法,再相练基础加即可.【详解】第一类:甲同学选择牛,乙有2种选法,丙有10种选法,选法有1×2×10=20(种),第二类:甲同学选择马,乙有3种选法,丙有10种选法,选法有1×3×10=30(种),所以共有20+30=50(种)选法.故选:B.3.(2021·全国·高二课时练习)如图所示,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同,则不同的涂色方法共有________种.(用数字作答)【答案】750【分析】由分步计数原理即得.【详解】首先给最左边的一个格子涂色,有6种选择,左边第二个格子有5种选择,第三个格子有5种选择,第四个格子也有5种选择,根据分步乘法计数原理得,共有6×5×5×5=750(种)涂色方法.故答案为:7504.(2021·全国·高二课时练习)如图所示,由连接正八边形的三个顶点而组成的三角形中与正八边形有公共边的三角形有________个.【答案】40【分析】根据分类加法计数原理即可求解.【详解】满足条件的有两类:第一类:与正八边形有两条公共边的三角形有m1=8个;第二类:与正八边形有一条公共边的三角形有m2=8×4=32个,所以满足条件的三角形共有8+32=40个.故答案为:405.(2021·全国·高二课时练习)1.计算:(1)将2封信投入4个邮箱,每个邮箱最多投一封,共有多少种不同的投法?(2)将2封信随意投入4个邮箱,共有多少种不同的投法?【答案】(1)12;(2)16【分析】(1)(2)用分步乘法原理求解.【详解】(1)将2封信投入4个邮箱,每个邮箱最多投一封,第一封信有4种选择,第二封有3种⨯=(种);选择,答案为4312⨯=(种).(2)将2封信随意投入4个邮箱,则每封信都有4种选择,所以共有44166.(2021·全国·高二课时练习)如图,把硬币有币值的一面称为正面,有花的一面称为反面.拋一次硬币,得到正面记为1,得到反面记为0.现抛一枚硬币5次,按照每次的结果,可得到由5个数组成的数组(例如若第一、二、四次得到的是正面,第三、五次得到的是反面,1,1,0,1,0,则可得不同的数组共有多少个?则结果可记为()【答案】32【分析】利用分步乘法计数原理求得正确答案.【详解】依题意可知不同的数组共有5⨯⨯⨯⨯==个.222222327.(2021·全国·高二课时练习)有不同的红球8个,不同的白球7个.(1)从中取出一个球,共有多少种不同的取法?(2)从中取出两个颜色不同的球,共有多少种不同的取法?【答案】(1)15(2)56【分析】(1)分别计算出取出一个红球、取出一个白球的方法种数,利用分类加法计数原理可得结果;(2)利用分步乘法计数原理可求得结果.(1)解:从中取出一个红球,有8种取法,从中取出一个白球,有7种取法,+=种不同的取法.由分类加法计数原理可知,从中取出一个球,共有7815(2)解:从中取出一个红球,有8种取法,从中取出一个白球,有7种取法,由分布乘法计数原理可知,从中取出两个颜色不同的球,共有7856⨯=种不同的取法. 8.(2021·全国·高二课时练习)有一项活动,需从3位教师、8名男同学和5名女同学中选人参加.(1)若只需1人参加,则有多少种不同的选法?(2)若需教师、男同学、女同学各1人参加,则有多少种不同的选法?【答案】(1)16(种);(2)120(种).【分析】(1)利用分类加法原理求解(1)利用分步乘法原理求解【详解】(1)选1人,可分三类:第1类,从教师中选1人,有3种不同的选法;第2类,从男同学中选1人,有8种不同的选法;第3类,从女同学中选1人,有5种不同的选法.共有3+8+5=16(种)不同的选法.(2)选教师、男同学、女同学各1人,分三步进行:第1步,选教师,有3种不同的选法;第2步,选男同学,有8种不同的选法;第3步,选女同学,有5种不同的选法.共有3×8×5=120(种)不同的选法.9.(2021·全国·高二课时练习)若直线方程Ax+By=0中的A,B可以从0,1,2,3,5这五个数字中任取两个不同的数字,则方程所表示的不同直线共有多少条?【答案】14条【分析】分类讨论A或B中有一个为0时和都不取0时的情况,根据计数原理即可求解.【详解】分两类完成:第一类:当A 或B 中有一个为0时,表示直线为x =0或y =0,共有2条;第二类:当A ,B 都不取0时,直线Ax +By =0被确定需分两步完成:第一步,确定A 的值,从1,2,3,5中选一个,共有4种不同的方法;第二步,确定B 的值,共有3种不同的方法.由分步乘法计数原理,共确定4×3=12(条)直线.由分类加法计数原理,方程所表示的不同直线有2+12=14(条).10.(2021·全国·高二课时练习)从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种,分别种在不同土质的三块土地上,其中黄瓜必须种植,求有多少种不同的种植方法.【答案】18种【分析】方法一:(直接法)分别考虑黄瓜种在第一块、第二块、第三块土地上的不同的种植方法,再运用加法原理可求得所有的不同种植方法.方法二:(间接法)先求得从4种蔬菜中选出3种,种在三块地上的不同的种植方法,再减去不种黄瓜的不同的种植方法,由此可求得答案.【详解】解:方法一:(直接法)若黄瓜种在第一块土地上,则有3×2=6(种)不同的种植方法.同理,黄瓜种在第二块、第三块土地上,均有3×2=6(种)不同的种植方法.故不同的种植方法共有6×3=18(种).方法二:(间接法)从4种蔬菜中选出3种,种在三块地上,有4×3×2=24(种),其中不种黄瓜有3×2×1=6(种),故共有不同的种植方法24-6=18(种).1.(2020·江苏扬州中学高一月考)已知集合,若A ,B 是P 的两个非空子集,则所有满足A 中的最大数小于B 中的最小数的集合对(A ,B )的个数为( )A .49B .48C .47D .46【答案】A【解析】集合知:1、若A 中的最大数为1时,B 中只要不含1即可:的集合为,而有 种集合,集合对(A ,B )的个数为15;2、若A 中的最大数为2时,B 中只要不含1、2即可:{}1,2,3,4,5P ={}1,2,3,4,5P =A {1}B 42115-=练提升的集合为,而B 有种,集合对(A ,B )的个数为;3、若A 中的最大数为3时,B 中只要不含1、2、3即可:的集合为,而B 有种,集合对(A ,B )的个数为;4、若A 中的最大数为4时,B 中只要不含1、2、3、4即可:的集合为,而B 有种,集合对(A ,B )的个数为;∴一共有个,故选:A2.(2021·全国·高二课时练习)一个同心圆形花坛,分为两部分,中间小圆部分种植草坪和绿色灌木,周围的圆环分为n (n ≥3,n ∈N *)等份,种植红、黄、蓝三种颜色不同的花,要求相邻两部分种植不同颜色的花.(1)如图①,圆环分成3等份,分别为a 1,a 2,a 3,则有多少种不同的种植方法?(2)如图②,圆环分成4等份,分别为a 1,a 2,a 3,a 4,则有多少种不同的种植方法?【答案】(1)6种;(2)18种.【分析】(1)利用分步计数原理求解即可.(2)首先根据题意分成两类:第一类a 1,a 3不同色和第二类a 1,a 3同色,分别计算各类的得数再相加即可.【详解】(1)先种植a 1部分,有3种不同的种植方法,再种植a 2,a 3部分.因为a 2,a 3与a 1的颜色不同,a 2,a 3的颜色也不同,所以由分步乘法计数原理,不同的种植方法有3×2×1=6(种).(2)当a 1,a 3不同色时,有3×2×1×1=6(种)种植方法,A {2},{1,2}3217-=2714⨯=A {3},{1,3},{2,3},{1,2,3}2213-=4312⨯=A {4},{1,4},{2,4},{3,4},{1,2,4},{1,3,4},{2,3,4},{1,2,3,4}1211-=818⨯=151412849+++=当a 1,a 3同色时,有3×2×1×2=12(种)种植方法,由分类加法计数原理得,共有6+12=18(种)种植方法.3.(2021·全国·高二单元测试)已知集合{}3,2,1,0,1,2M =---,()(),,P a b a b M ∈表示平面上的点,问:(1)P 可表示平面上多少个第二象限的点?(2)P 可表示多少个不在直线y x =上的点?【答案】(1)6(个);(2)30(个).【分析】(1)由分步乘法原理求第二象限的点的个数,(2)依次确定横坐标和纵坐标的可能取法,由分步乘法原理求不在直线y x =上的点的个数.【详解】(1)因为P 表示平面上第二象限的点,故可分两步:第一步,确定a ,a 必须小于0,则有3种不同的情况;第二步,确定b ,b 必须大于0,则有2种不同的情况;根据分步乘法计数原理,第二象限的点共有326⨯=(个).(2)因为P 表示不在直线y x =上的点,故可分两步:第一步,确定a ,有6种不同的情况;第二步,确定b ,有5种不同的情况.根据分步乘法计数原理,不在直线y x =上的点共有6530⨯=(个).4.(2021·全国·高二单元测试)某同学计划用不超过30元的现金购买笔与笔记本.已知笔的单价为4元,笔记本的单价为5元,且笔至少要买2支,笔记本至少要买2本,问不同的购买方案有多少种?【答案】7【分析】根据分类加法计数原理求解即可.【详解】设购买笔x 支,笔记本y 本,则453022x y x y +≤⎧⎪≥⎨⎪≥⎩,得305242y x y -⎧≤≤⎪⎨⎪≥⎩,将y 的取值分为三类:①当2y =时,25x ≤≤,因为x 为整数,所以x 可取2,3,4,5,共4种方案.②当3y =时,1524x ≤≤,因为x 为整数,所以x 可取2,3,共2种方案;③当4y =时,522x ≤≤,因为x 为整数,所以x 只能取2,只有1种方案.由分类加法计数原理得不同的购买方案有4217++=(种).5.(2021·全国·高二课时练习)如图所示,有些共享单车的密码锁是由4个数字组成的,你认为共享单车的密码锁能设置成由3个数字组成吗?5个数字呢?为什么?【答案】3个数字的不合适,5个数字的合适;【分析】根据分步乘法计数原理求出所有的密码组合数,再根据概率分析可行性;【详解】解:如设成3个数字,则一共有1010101000⨯⨯=种组合,组合数不是很大,随便尝试一次开锁,打开锁的概率11000P =,打开锁的概率比较大,不合适;如设成5个数字,则一共有1010101010100000⨯⨯⨯⨯=种组合,组合数比较大,随便尝试一次开锁,打开锁的概率1100000P =,打开锁的概率比较小,合适;6.(2021·全国·高二课时练习)过三棱柱任意两个顶点的直线共15条,其中异面直线有多少对?【答案】36【分析】如图,分四类进行计数,求出对应的数目,加起来即可.【详解】如图,在三棱柱111ABC A B C -中,分四类进行计数:与上底面111111A B A C B C ,,异面的直线有35=15⨯对;与下底面的AB AC BC ,,异面的直线有9对(除去与上底面的);与侧棱111AA BB CC ,,异面的直线有6对(除去与下底面的);侧面对角线之间成异面直线的有6对.由分类加法计数原理,知共有异面直线共有15966=36+++对.7.(2021·全国·高二课时练习)计算(1)用1,2,3,4,5,6可以排成多少个数字不重复的两位数?(2)用1,2,3,4,5,6可以排成多少个数字可以重复的两位数?【答案】(1)30(2)36【分析】(1)用数字1,2,3,4,5,6可组成没有重复数字的两位数,用两步完成,第一步十位数字有6种选择,然后第二步个位数字在剩下的5个数字中选择有5种方法,运用乘法原理,即可得解,(2)按照分步乘法计数原理计算可得;(1)解:第一步十位数字有6种选择,然后第二步个位数字在剩下的5个数字中选择有5种方法,运用乘法原理得6530⨯=.所以可以排成30个不重复的两位数;(2)解:第一步十位数字有6种选择,然后第二步个位数字有6种选择,运用乘法原理得6636⨯=.所以可以排成36个可以重复的两位数;8.(2021·全国·高二课时练习)已知n 是一个小于10的正整数,且由集合{},A x x x n =∈≤N 中的元素可以排成数字不重复的两位数共25个,求n 的值.【答案】5【分析】用列举法表示集合A ,再按照分步乘法计数原理得到方程,解得即可;【详解】解:因为n 是一个小于10的正整数,且{},A x x x n =∈≤N ,所以{}0,1,2,,A n = ,所以从集合A 中的元素选出两个数组成两位数,则十位有n 种选法,个位有11n +-种选法,按照分步乘法计数原理可得一共有()11n n +-个,所以()1125n n +-=,解得5n =或5n =-(舍去)9.(2021·全国·高二课时练习)(1)4名同学选报跑步、跳高、跳远三个项目,每人报一项,共有多少种报名方法?(2)4名同学选报跑步、跳高、跳远三个项目,每项限报一人,且每人至多报一项,共有多少种报名方法?(3)4名同学争夺跑步、跳高、跳远三项冠军,共有多少种可能的结果?【答案】(1)81(种);(2)24(种);(3)64(种).【分析】由分步乘法计数原理即得.【详解】(1)要完成的是“4名同学每人从三个项目中选一项报名”这件事,因为每人必报一项,4人都报完才算完成,所以按人分步,且分为四步,又每人可在三项中选一项,选法为3种,所以共有3×3×3×3=81(种)报名方法.(2)每项限报一人,且每人至多报一项,因此跑步项目有4种选法,跳高项目有3种选法,跳远项目只有2种选法.根据分步乘法计数原理,可得不同的报名方法有4×3×2=24(种).(3)要完成的是“三个项目冠军的获取”这件事,因为每项冠军只能有一人获得,三项冠军都有得主,这件事才算完成,所以应以“确定三项冠军得主”为线索进行分步,而每项冠军的得主有4种可能结果,所以共有4×4×4=64(种)可能的结果.10.(2021·全国·高二课时练习)“回文数”是指从左到右读与从右到左读都一样的正整数.如22,121,343,94249等.显然,2位数的回文数有9个,即11,22,33,…,99;3位数的回文数有90个:101,111,121,…,191,202,…,999.求:(1)4位数的回文数个数;(2)21n +位数的回文数个数.【答案】(1)90(2)910n⨯【分析】(1)对于4位数的回文数,只需排好前2位即可确定回文数,首先列举出第一项为1的四位回文数的个数,即可知所有4位数的回文数个数;(2)根据题设,对于奇数个数的回文数,先排好中间的数字,再在两侧对其中一侧排数即可得所有回文数的个数.(1)由题设,四位数回文:1001,1111,1221,1331,1441,1551,1661,1771,1881,1991,...∴共有90个.(2)n+位数,则中间的数字有10种选法,而两侧的数字只需排好一侧,则另一侧确定,21n-都有10种选法,不妨排前n位数字,显然第一位数字有9种选法,其余1∴共有910n⨯个回文数.练真题1.(山东省2018年普通高校招生(春季))景区中有一座山,山的南面有2条道路,山的北面有3条道路,均可用于游客上山或下山,假设没有其他道路,某游客计划从山的一面走到山顶后,接着从另一面下山,则不同走法的种数是()A. 6 B. 10 C. 12 D. 20【答案】C【解析】先确定从那一面上,有两种选择,再选择上山与下山道路,可得不同走法的种数是2×2×3 =12.因此选C.2.(2013·山东高考真题(理))用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为( )A.243B.252C.261D.279【答案】B【解析】由分步乘法原理知:用0,1,…,9十个数字组成的三位数(含有重复数字的)共有9×10×10=900,组成无重复数字的三位数共有9×9×8=648,因此组成有重复数字的三位数共有900-648=252.3.(2012·北京高考真题(理))从0,2中选一个数字.从1,3,5中选两个数字,组成无重复数字的三位数.其中奇数的个数为( )A.24 B.18 C.12 D.6【答案】B【解析】由于题目要求的是奇数,那么对于此三位数可以分成两种情况:奇偶奇;偶奇奇.如果是第一种奇偶奇的情况,可以从个位开始分析(3种选择),之后十位(2种选择),最后百位(2种选择),共12种;如果是第二种情况偶奇奇,分析同理:个位(3种情况),十位(2种情况),百位(不能是0,一种情况),共6种,因此总共12+6=18种情况.4.(2016全国甲理5)如图所示,小明从街道的处出发,先到处与小红会合,再一起到位于处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )A.24B.18C.12D.9【答案】B 【解析】从的最短路径有种走法,从的最短路径有种走法,由乘法原理知,共种走法.故选B .5.(2012·四川高考真题(文))方程ay =b 2x 2+c 中的a,b,c ∈{−2,0,1,2,3},且a,b,c 互不相同,在所有这些方程所表示的曲线中,不同的抛物线共有( )A .28条B .32条C .36条D .48条【答案】B【解析】方程ay =b 2x 2+c 变形得,若表示抛物线,则所以,分b=-2,1,2,3四种情况:(1)若b=-2,; (2)若b="2,"以上两种情况下有4条重复,故共有9+5=14条;同理 若b=1,共有9条; 若b=3时,共有9条.综上,共有14+9+9=32种6.(2011·安徽高考真题(理))设集合{}1,2,3,4,5,6,A ={}4,5,6,7,B =则满足S A ⊆且S B ≠∅ 的集合S 的个数为( )A .57B .56C .49D .8【答案】B【解析】E FG E F →6F G →36318⨯=由题意可知集合S 可以表示为S M N = 的形式,其中M 为集合{}1,2,3的非空子集,N 为集合{}4,5,6的非空子集,由子集个数公式可得,集合M 的个数为7个,集合N 的个数为7个,则集合S 的个数为7856⨯=个.故选:B .。

龙源期刊网 青铜神树作者:张馨月来源:《环球人文地理》2015年第12期“沉睡数千年,一醒惊天下。
”这是张爱萍将军对“三星堆遗址”的称赞。
发现“三星堆遗址”可谓石破天惊,从中出土的文物无一不是稀世之宝,出自其中的“青铜神树”更是其代表性文物之一。
青铜神树出土于1986年,共有8棵,属于夏代晚期的青铜器。
其中一号神树高达3.96米,拥有3层枝叶,每层均有3根树枝,树枝上接有由青铜铸就的花果,或上翘,或下垂,姿态各异,惟妙惟肖。
每一根树枝上,均站立着一只鸟,总共9只,其原型则是中国古代神话中的“太阳神鸟”。
神树的下部,悬吊着一条巨龙,龙头朝下,龙尾朝上,姿态雄伟。
出土的二号神树仅保留着下半段,其余部分则形态不明。
在保留尚好的下半部分,由3条树根组成的底座上,各拥有一个跪坐人像,人像双手前伸,似乎正托着什么东西,可见二号神树与一号神树的造型截然不同,但由于其余部分损毁严重,二号神树的全貌究竟为何,至今不得而知。
而其余6棵神树,同样因为损毁严重而无法复原。
事实上,形态完整的一号神树在刚出土时,同样有多处损毁,由于长期处于被夯实的土层中,其变形十分严重,树干断成了;3;段,树枝则断为;18;段,鸟、龙、花果的碎片更是难以计数。
如此严重的损毁,自然就为修复工作带来了极大的不便,以至于从出土的1986年到10年后的1996年,一号神树的修复工作才得以完成。
青铜神树的形态精密细致,吸引了无数考古学家的注意,据研究,这8棵神树的原型均应出自中国古代神话传说当中的神树,由于其余几棵神树的形态尚不可知,因此考古专家只确定了一号神树的原型;:扶桑。
扶桑学名朱槿,本是一种观赏性植物,但根据相关文献记载,在上古时期,扶桑是生长在东方的太阳树,在远古传说中,天上有10个太阳,每一个太阳都是一只通体发光的神鸟,每一天都有一只太阳神鸟从扶桑树上升起,其余;9;只则栖息在树上,故扶桑也被称为“太阳神树”。
那时,崇拜神树是人类的重要信仰和习俗,因此,以“太阳神树”的原型扶桑铸就的青铜神树,无疑是上古时期的一件祭祀器物。
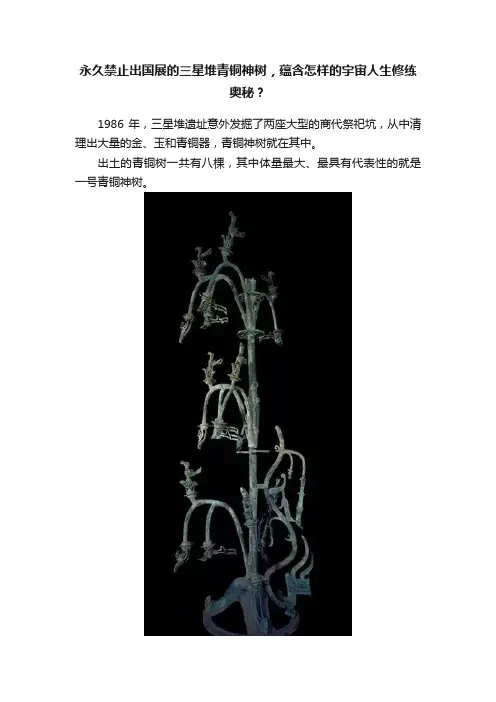
永久禁止出国展的三星堆青铜神树,蕴含怎样的宇宙人生修练奥秘?1986年,三星堆遗址意外发掘了两座大型的商代祭祀坑,从中清理出大量的金、玉和青铜器,青铜神树就在其中。
出土的青铜树一共有八棵,其中体量最大、最具有代表性的就是一号青铜神树。
这棵青铜树现残高359厘米,顶部有残缺,据推测,实际高度应为396厘米。
全树采用分段铸造法制成,运用了套铸、铆铸、嵌铸、铸接等当时最为先进的手法,可谓青铜铸造工艺的集大成者。
神树由底座、树和龙三部分组成,底座呈穹窿形,由三面弧边三角状镂空虚块面构成,构拟出三山相连的“神山”意象,座上铸饰象征太阳的“☉”纹和云气纹。
▲ 青铜神树上的神鸟。
树铸于“神山之巅”的正中,分为三层,每层有三根枝条,共九枝上面有镂空花纹的小圆圈和花蕾,花蕾上各有一只昂首翘尾的神鸟,共有九只。
树的顶部有残缺,专家推测,顶部也应该有一只鸟站立于其上,总共十只神鸟。
在青铜树的枝干上可以清晰地看到有一些用以垂挂器物的穿孔,人们推测,器物坑中的一些小型青铜发声器也许原本是悬挂在铜树上的。
2其二曰建木,在中央《吕氏春秋·有始》中记载:“白民之南,建木之下,日中无影,呼而无响,盖天地之中也。
”《淮南子·墬形训》中则说:“建木在都广,众帝所自上下。
”天地的中心是一棵树,叫做建木,它在太阳下面没有影子,风吹过也不会有声音,神仙们通过这棵树往来于天地之间。
高近4米的青铜树顶天立地,树间攀援的龙,或许就是巫师们驾乘着上天入地的坐骑。
今天的许多文学作品也沿用了这个传说,电视剧《天外飞仙》《仙剑奇侠传》、动画《大鱼海棠》中,天地相连之处就是一棵树。
鸟首铜铃,怀疑原本是悬挂在神树上的神话传说中的“通天神树”这些青铜树为什么被称为“神树”呢?在我国的古史神话中,树和日月运行、天地相通有着密切的联系,《山海经》等志怪书中就记载了很多种。
1其一曰扶桑,在东方《山海经·海外东经》中说:“汤谷上有扶桑,十日所浴,在黑齿北。
三星堆中青铜神树解释和猜想《三星堆中青铜神树:解释与猜想》在中国四川省广汉市附近的三星堆遗址中,考古学家们发现了许多令人惊叹的文物,其中一个引人注目的发现是出土的青铜神树。
这座神秘的青铜铸造物引起了人们广泛的解释和猜想,为我们揭示了古代文明的一角。
青铜神树是一件高约四米的青铜铸造物,具有树干和树枝的形态,树冠缀满了各种动物和神秘人物的雕刻。
这些动物和人物的表情栩栩如生,栩栩如生的细节使得这件艺术品更加令人惊叹。
关于青铜神树的解释,目前学界存在很多争议。
一种观点认为,青铜神树是古人的宗教信仰的象征。
树是自然界的生命象征,而树干上的动物和人物则代表了宇宙万物。
这种解释认为,青铜神树是对宇宙万物和自然界的崇拜,是古代人类对环境的一种神圣敬畏。
另一种解释认为,青铜神树可能是古人对社会组织的象征。
树枝的分叉被理解为家族或社会的分支,人物和动物的雕刻代表了不同的氏族或社群。
这种解释认为,青铜神树是古代人类对社会组织和集体意识的表达,是一种对共同生活的理解和呈现。
除了以上的解释外,还有一些学者猜测,青铜神树可能是古人对宇宙起源的揣测。
树冠上的雕刻可能代表了宇宙中的星球和神秘的天体。
青铜神树此时被解读为一种对宇宙起源的探索和思考,是古代人类对未知世界的一种表达。
尽管这些解释和猜想各有道理,但关于青铜神树真正含义的争议目前仍在进行中。
为了更好地理解这一艺术品,进一步的考古研究和学术探索是必要的。
通过更多的发掘和研究,我们相信会有更多的明确解释和猜想出现,为我们揭示古代文明的奥秘。
《三星堆中青铜神树:解释与猜想》带领我们走进了古代文明的一部分。
青铜神树的发现和研究不仅展示了古人的智慧和艺术造诣,也引发了人们对古代文化的思考和探求。
相信随着进一步的研究,我们将能够更好地理解这一神秘的青铜铸造物背后的故事。
穿梭于天地间的精灵文/邹 鹏1986年三星堆遗址的发现,为我们揭开了3000多年前古蜀王国的神秘面纱。
三星堆遗址中出土了丰富多样、设计奇特的动物造型文物,其中,阵容强大的鸟类一族最为引人注目。
三星堆遗址出土的鸟类造型文物有10多种不同的形态,它们或简约,或精巧,或秀雅,或古朴,千姿百态,美不胜收!这些充满灵气的文物不仅是精美的艺术珍品,而且为我们展现了古蜀人丰富的精神世界。
在古蜀人心目中,这些鸟既是穿梭于天地间的精灵,又是沟通人和神的使者。
众鸟之王——青铜大鸟头在三星堆遗址出土的众多鸟类造型文物中,青铜大鸟头是最大的一件。
它有40厘米高,设计风格简约。
这只大鸟紧闭着嘴,圆睁着眼,精神抖擞,颇具众鸟之王的气质。
器物出土时,考古学家发现它的嘴和眼珠周围都保留有红色的朱砂,看来古人制作的有可能是一只彩色的神鸟。
仔细观察,你会发现大鸟的颈部下端有三个小圆孔。
考古学家以此推断,这只大鸟很可能是当时某个部族的族徽,古蜀人用小圆孔就可以将它固定在建筑或者其他物体之上了。
三星堆新发现青铜大鸟头这只颇具王者之气的大鸟,在3000多年前的古蜀人心中有着怎样独特的象征意义呢?大家看,大鸟弯钩状的嘴看上去与鱼鹰十分接近,因此有考古学家推测它可能代表了传说中的第三代蜀王——鱼凫,也有人认为这是当时鱼凫族的标志之一。
独具想象力的作品——青铜凤鸟与青铜大鸟头简约生动的设计风格不同,三星堆出土的很多凤鸟造型的器物精巧、秀雅,有很强的观赏性和艺术性。
在众多文物中,有一件青铜凤鸟,它头上的羽冠很有特色。
这只鸟的身体呈流线型,双眼浑圆,嘴又长又尖,直立的羽冠像一排迎风招展的旌旗,看上去它似乎正在聚精会神地看着什么,一动不动,展现着静态美。
从残断的双腿来看,它可能是与其他器物组合使用的,估计是某件重要器物上的附件或者装饰物。
另外一件青铜凤鸟同样极具特色。
只见傲立的小鸟身体修长,弯弯的嘴,圆圆的眼,身上飞扬的羽翅犹如跳动的青铜凤鸟青铜凤鸟铜人首鸟身像鸟形青铜铃雕刻有鸟纹的金杖陶鸟头勺把。
青铜神树“复活”记作者:秋慈来源:《科学之友》2022年第03期青铜神树的发现是个偶然。
1986年7月18日,四川省广汉市当地一家砖厂工人在取土做砖坯时,无意中挖到了三星堆1号祭祀坑的一个角,出土了一些玉器和石器,随后,考古队组织正式发掘,1号祭祀坑正式与世人见面。
仅仅一个月后,砖厂工人在取土时又挖到了一个青铜头像的耳朵,就向考古队汇报。
至此,2号祭祀坑也重见天日。
2号祭祀坑中共出土了8棵青铜神树,其中修复得最完整的是1号青铜神树,这也是目前考古发现中体量最大的青铜文物。
神树由底座、树和龙三部分组成,采用分段铸造法铸造,同时使用了套铸、铆铸、嵌铸等工艺,通高3.96米,树干顶部及龙身后段略有残缺。
神树底座呈穹隆形,圆形底盘上由三叉支架构拟出山形,树座上绘有精美的云气纹,寓意“神山”。
树铸于“神山”之巅,卓然挺拔,直接天宇。
树分3层,每层3枝,共9枝。
树枝柔和垂下,每枝中部又伸出果枝,枝上有镂空花纹的小圆圈和花蕾。
向上的9个花蕾上各站一只昂首翘尾的小鸟,全树共9只神鸟。
树侧则有一条逶迤而下的长龙,整条龙造型怪异诡谲,莫可名状。
1号青铜神树青铜龙局部如此精美的大型青铜器,放到现在都是罕见的工艺品,更遑论3 000多年前。
不过,1号青铜神树刚出土的时候可并不是这么威风。
因为坑中的器物在掩埋前已经被人为敲碎,神树重见天日的时候,树干断为3截,树枝断成18截,鸟儿、果实等碎片多达上千片,层层叠叠散落一坑,根本没有人能想到它曾经的风采。
1986年10月,残破的青铜神树被运往四川省文物考古研究院,由文物修复专家杨晓邬带队修复。
“全是碎片,和泥土混在一起。
”年过七旬的杨晓邬仍能回忆起30多年前的场景。
他说,古人把精美的祭品敲断、火烧,然后埋进土坑,交付给神灵,而几千年后,这成了给文物修复师们出的难题。
首先要想办法让神树重新“站”起来,总重达150多千克的神树树干不仅折断,而且很多地方氧化严重,无法承受焊接。
杨晓邬想到一个办法,他和团队在四川省文物考古研究院修复室外面的天井里,搭起一个5米高的棚子和脚手架,围上塑料膜,盖上玻纤瓦,充当临时工作室。
一號青銅神樹前世傳奇專家評價
在一号青铜神树的前世传奇中,国宝守护人张晋将回到上古时期,演绎古蜀人卫皋带领族人穿越岷江山谷寻找栖息之地的故事。
《山海经·海外东经》记载:“汤谷有扶桑,十日所浴,九日居下枝,一日居上枝。
”意思就是说,在东海汤谷生长着一棵名叫“扶桑”的神树,树上居住了十个太阳,每天由三足乌驮着轮流值日。
每当一个太阳升起,其他九个就在神树上休息。
这与三星堆一号青铜神树上九只神鸟的造型不谋而合,因此专家们推测它很可能就是神树的实物标本。
节目中,陪伴三星堆走出蜀地、走向世界的前四川省文物管理局局长,将担任一号青铜神树的今生讲述人,为观众讲述三星堆文物的“环球旅行”。
据介绍,“三星堆文物自1986年出土后,共举办了43次外展,足迹遍及五大洲,是继兵马俑之后西方观众最喜爱的展览。
”。
三星堆地下秘密:还有七棵青铜神树等待发现1986年夏,在三星堆遗址发现大型青铜神树二件,被称为“I号大型神树”和“II号大型神树”,同时出土的还有青铜小型神树残件四件,修复完毕后发现共有8棵青铜。
如果根据《尚书》、《山海经》的记载,三星堆青铜神树应该有十二颗小青铜树,三颗大青铜树名扶木、若木、建木,当为十五棵。
目前已出土8颗,还有7颗在地下。
《山海经》里记录有日月出入之山共十四座。
《山海经大荒东经》记载了七座日月所出之山,六座只有山名,一座有山名,还有树名:汤谷上有扶木。
1、东海之外,大荒之中,有山名曰大言,日月所出。
2、大荒之中,有山名曰合虚,日月所出。
3、大荒中有山,名曰明星,日月所出,4、大荒之中,有山名曰鞠陵于天、东极、离暓,日月所出。
5、大荒之中,有山名曰孽摇頵羝。
上有扶木,柱三百里,其叶如芥。
有谷曰温源谷,汤谷上有扶木,一日方至,一日方出,皆载于乌。
6、大荒之中,有山名曰猗天苏门,日月所出。
7、东荒之中,有山名曰壑明俊疾,日月所出《山海经大荒西经》记载了七座日月所入之山,六座只有山名,其中一座有山名,还有树名:青树,名曰柜格之松。
1、西海之外,大荒之中,有方山者,上有青树,名曰柜格之松、日月所出入也。
2、大荒之中,有山名曰丰沮玉门,日月所入。
3、大荒之中,有龙山,日月所入。
4、大荒之中,有山名曰月山,天枢也。
吴姖天门,日月所入。
5、大荒之中,有山名曰鏖鏊钜,日月所入者。
6、大荒之中,有山名曰常阳之山,日月所入。
7、大荒之中,有山名曰大荒之山,日月所入。
我们常说太阳东升西落,月亮西出东隐,那只是模糊的说法,太阳月亮的升降位置因为地球的自转和公转,随四季而移动。
冬至日,太阳直射南回归线,太阳在东南方升起,从西南方落下;春分与秋分,太阳直射赤道,正是东升西落;夏至日,太阳直射北回归线,从东北方升起,落入西北方。
《淮南子天文训》:日冬至,日出东南维,入西南维;至春秋分,日出东中,入西中;夏至,出东北维,入西北维,至则正南。
三星堆出现的“天鸟”的由来作者:傅希春笔名:颂夏龙马负图作为华夏重要的神话传说,能流传到今天,说明《河图》是⼀个⾮常重要的远古物件,与华夏⽂明有关联,⼜因华夏⽂明与盘古(固)开天地中的“神斧”有关联,因⽽我们可作出这样的判断,《河图》极可能也与盘古(固)开天地中的“神斧”有关联。
⼏千年来,我们这个世界之所以未搞明⽩盘古(固)开天地真相,是因为我们这个世界⼀直没搞明⽩盘古(固)开天地隐语中的“神斧”到底是什么。
“神斧”劈向四⽅,分出了天地。
搞清楚“神斧”的真相,是揭秘盘古(固)开天地隐语的关键,也是解读《圣经·创世纪》中“起初神创造天地”这句话的关键。
远古的“神斧”之形,可从甲45号墓出⼟的这个蚌塑⼈⾻北⽃,在出⼟时极可能被⼈动过,上古⼈们下葬时不可能这样摆放。
这个蚌塑⼈⾻北⽃的⽃柄只能⽤⼀根⼈⾻,北⽃只有⼀根⽃柄,另⼀根⼈⾻是不是并排在⼀起的,作为“帝王命⾻”的那根⼈⾻与作为北⽃⽃柄的那根⼈⾻应是近乎垂直摆放的,只有近乎垂直的摆放,才能我们会发现这蚌塑⼈⾻北⽃就是“斧”之形。
“斧”,有北⽃之象,在远古,古⼈⽤“斧”象征天上的北⽃,这应是⼥娲⽒开创华夏⽂明的重要天机。
“神斧”劈向四⽅,即,在傍晚,北⽃的⽃柄指东为春,指南为夏,指西为秋,指北为冬,北⽃的旋转,引发了远古先哲开天地创世的⼼智。
我在研究我国纳西族东巴教⽂化时,发现了我国上古佛教七祖虞象在古蜀地弘扬佛法的东巴绘画(虞象是4000多年前寞瞽叟的⼆⼦,舜的弟弟,被舜封于蜀,在北起长江南⾄南海、印度洋的⼴⼤区域⾥做蜀王),发现了⼀些东巴⽂字中带有华夏远古、上古⽂明的信息,古蜀三星堆⽂化是远古华夏⽩夷⽂化的延续,纳西东巴⽂化是古蜀三星堆上古⽂化的延续,纳西东巴教⼜是未受到后世西藏佛教很⼤影响的原⽣态佛教(只是历史上的纳西⼈在周王朝伐荆楚灭佛后不敢再称“佛教”⽽已),因此,深⼊研究纳西东巴教的⽂化现象和发展脉络,有助于我们还原三星堆上古华夏⽩夷⽂化的本真。
“三星堆遗址”是我国古代的一座著名“遗址”,相信很多读者都会想到,这座遗址距今已有5000至3000年历史,被称为20世纪人类最伟大的考古发现之一。
但专家在发掘三星堆遗址,曾遇到一个大难题,出土的1号青铜神树上,为何只有九只鸟,剩下的一只去了哪里?
(本文所有图片,全部来自网络,感谢原作者,如侵犯您的权利,请联系本号作者删除。
图片
与内容无关)
1929年,四川省广汉市西北地区的一位农民,在田间挖蓄水沟时,意外地发现一个人造石洞,里面竟有好几块玉器。
紧接着,农民挖出宝物的消息便被传出,大量的古董商人蜂拥而至。
看到珍贵的玉器时,他们并没有察觉到,发现玉器的地方,还沉寂着更多的珍贵文物。
1980年5月,四川省的文物专家们,接到上级命令,再次对三星堆进行发掘,而这次发掘,
专家们出土了大量的陶器、石器、玉器等文物。
两年后,相关部门决定对发掘“三星堆遗址”
项目进行专项拨款。
经过长时间的发掘,专家们在二号祭坑中又取得了一个巨大的收获,他们发现一件“与众不同”的文物,它就是“1号大型铜神树”。
1号大型铜神树是用青铜铸造而成的物件,树干残高359厘米,通高396厘米。
该件文物由
四部分构成:底座、树、金乌、龙。
在铸造的过程中,工匠采用了套铸、铆铸、嵌铸等工艺。
正因如此,通神树才会如此精美。
专家看到“1号大型铜神树”后,心生疑惑,铜树上共有九只金乌(传说中的神鸟),难道是有什么寓意吗?根据相关传说记载,铜树上应该有十只金乌,缺少的一只去哪了?专家们通过专业的分析,共给出三个原因。
一、金乌在值日
根据《山海经•大荒东经》中的描述,太阳是无法移动的,所以,十个太阳是由金乌背负着,轮班上岗,十个太阳会交替着,每天按着时辰上升或下降。
正因如此,我们才能看到日出和日落。
铜树上有九只金乌,而第十只金乌背负太阳去带给人间光明去了,所以,铜树上才没有它的身影。
二、出土时被毁掉
专家们不会主动地发掘文物,只有当它们遭到破坏时,专家才会进行抢救式发掘。
文物出土很容易,但保存却非常困难。
在发掘三星堆遗址的过程中,专家并不能保障所有文物都被完整取出。
铜神树的树干残高359厘米,所以,专家们推测,第十只金乌可能在出土时,遭到毁坏或深埋底下被腐蚀。
三、并不是太阳神之意
铜树共分为三层,每层三枝,共九枝。
专家认为,每层的三支代表祖、父、孙的一个传承周期,铜枝上的分叉代表同辈之间关联。
而铜树上的九只鸟,并不是用来背负太阳的,而是有
关联的独立个体,它们代表着古蜀国不同时代的九代蜀王的传承顺序。
无论“1号大型铜神树”有没有第十只金鸟,小编相信各位读者心中早就有了答案。
如今,这
件文物被收藏在三星堆博物馆,它独有的魅力,让众多游客流连忘返。
如果大家对它感兴趣,可以亲自去看一看,说不定,您就能找到第十只金乌的秘密。