基本模型网格节点分布

gambit网格划分基本类型：（一）Mesh Face ：面划分Element :Quad:四边形网格Tri：三角形网格Quad/Tri：四边形和三角形网格混合Type :1、map：建立规则的四边形结构性网格2、submap：将不规则的区域划分为几个规则的区域3、pave：非结构性网格4、Tri Primitive:将一个三角形区域划分为三个四边形区域，并同时划分为四边形网格5、Wedge Primitive:将一个楔形的尖端划分为三角形网格，沿着楔形向外辐射，划分为四边形网格（二）Mesh Volume：体划分Element :Hex:六面体网格Hex/Wedge：以六面体为主，在适当的位置包括楔形网格Tet/Hybrid:以四面体为主，在适当的位置上包括六面体、锥形和楔形网格Type :1、map：建立规则的结构化六面体网格2、submap：将不可结构化划分的体积进行分割，再建立map网格3、tet primitive：将四面体分成多个六面体，再对各区域建立map网格4、cooper：通过源面对整个体进行网格样式的扫描,适用于逻辑圆柱体5、stairstep：建立规则六面体网格和相应的微小体积来近似原来的几何体形状，椭圆体。

6、tgrid：将网格指定为四面体元素，但是在适当处可能包括六面体、金字塔形和楔形网格划分方法：（一）MESH FACE FORM1、Map Scheme:4*End+N*Side（1）Periodic(周期性) map Scheme: N*Side，针对圆柱面（2）Face（面）Mapple操作方法：(1)打开“Face Vertex form”对话框，选择用圆圈标注的点，将其修改为“S”类型；然后，打开“Mesh Face Form”对话框，划分网格。

或者(2)在“Mesh Face Form”对话框中，直接将schemme(框架)修改为“Map”。

4*End+L*Side+M*End+Corner+N*2*End+Reverse2、Submap:()()修改方法同2：“E ”改成“S ”。

0经典产品教程与实例详解m210二阶近似最好的结果用多个单元的线性近似好结果线单元?只支持线性变化的位移因此一个单元内为常应力?对单元扭曲高度敏感?如果仅对名义应力结果感兴趣则可接受二次单元?支持二次变化的位移及在一个单元内线性变化的应力?能代表曲边边界及曲面比线性单元更为准确
第八章: 创建节点单元模型与网格划分技术
• 网格划分的三个步骤:
– 定义单元属性(单元类型、实常数、材料属性). – 定义网格控制(控制网格密度). – 网格划分以前保存数据库. – 产生网格.
• 主要内容:
A. 多种单元属性 B. 控制网格密度 C. 改变网格 E. 六面体到四面体的过渡 F. 网格拖拉 G. 网格的扫略
D. 映射网格
ANSYS9.0经典产品教程与实例详解
M2-1
8.1创建有限元模型的两种方法
• 方法一：直接法，首先创建节点，然后利用节点创建单元, 单个和多个单元组成一个有限元模型。 • 方法二：几何模型网格划分法，首先创建或者导入CAD几何 模型，然后利用网格划分工具将其划分成单元网格 模型。
ANSYS9.0经典产品教程与实例详解
M2-2
8.2 单元库、单元类型与单元实常数
8.2.1单元库、单元类型
点单元 线单元 –梁 单元用于模拟螺栓、管件、C-sections、角钢或只需膜应力和弯曲应力的 任何 细长杆件。 质量单元MASS21
–杆单元 用于模拟弹簧、螺栓、预应力螺栓及桁架。 –弹簧 单元用于模拟弹簧、螺栓、细长部件或通过等效刚度替代复杂部件.
壳单元 –用于模拟薄板或曲面。 –一般来讲，细的定义依赖于应用，主要方向的尺寸至 少为其厚度的10倍
ANSYS9.0经典产品教程与实例详解
M2-3
• 二维实体单元:

k–ε 湍流模型
标准 k–ε (SKE) 模型 在工程应用中使用最为广泛的紊流模型 Robust 而且相对准确 包括用于可压缩性, 浮力, 燃烧, 等等子模型 局限性 ε 方程包括一个不能在壁面上计算的项. 因此, 必须使用壁面边界条件. 在流动有强烈的别离下一般表现不好,比方大曲率流线和大压力梯度 重正规化群 (RNG) k–ε模型 k–ε 方程中 的常数源自使用重正规化群理论. 包括以下子模型 解决低雷诺数下的特异粘度模型 源自对紊流 Prandtl / Schmidt数的代数公式的解析解 漩涡修正 对更复杂的剪切流来说比SKE 表现更好,比方高应变率，漩涡和别离的流
Rij uiuj
(Reynolds 压力张量)
Reynolds 应力是由附加未知的平均程序引进的,因此为了封闭控制方 程组系统它们必须被模拟 (涉及到平均流动属性).
方程封闭问题
RANS 模型能够在以下方法其中之一下封闭 (1) 漩涡粘性模型 (通过 Boussinesq 假设)
Rij
uiuj
fine mesh near surface & first cell at y+ = 1.
Grid for Flow Over a Cylinder
Prediction of Turbulent Vortex Shedding
Contours of effective viscosity eff = + t
Uk
Ui xk
p xi
2Ui
x jx j
Rij x j
其中 Rij uiu j
(雷诺应力)
时间平均湍流速度脉动通过基于经历常数和主流的信息来求解. 大涡模拟Large Eddy Simulation对大涡进展直接求解，而对小涡采

网格拓扑：关联块与实 体的点线 面，把对基本 块划分的网格节点投影到 实体中。（相对空间位置（节 点）的一一映射。）
基本块
2D:四边形块 3D:六面体块
•

安心+耐心
块 映射 实体
块 Block
点/Vertex 直边/Edge 平面/Face

Point / 点 Curve /曲线 Surface曲面
Patch Independent : 忽略小特征 ShrinkWrap :自动化消除特征 Delanney(beta) : 从表面到内部逐渐粗化 AutoBlock : 2D正交,网格贴近几何表面
• Compute Mesh-Surface Mesh Only（可更改划 分方法），检查网格质量 ； Edit Mesh-Display Mesh Quality
点击apply或ok，然后点击output——〉write/view input，打开uns文 件，output file 给出文件名，点击done。
AUTODYN 中ICEM网格的导入
• 1、新建文件：(File->设置文件名、几何特征、单位） • 2、选择填充材料：Material->Load->选材料 • 3、导入网格：Import->.zon(2D)/.geo,.k(3D)->Import all part • 4、填充材料：Compent->new->起名，选part,点add;
实体:简化

综合运用
旋转;对称;平移
增加插值元素
O grid;C grid; L grid
点:劈分/合并;移动;关联| 增加辅助点
线:劈分;关联
| 增加辅助线

谈谈FLUENT中⽹格质量的问题谈谈Fluent中⽹格质量的问题中⽹格质量的问题我们在fluent计算中经常碰到⽹格划分质量的问题，如果要得到⾼质量的⽹格划分需要注意哪些问题？其具体的依据是什么啊？个⼈认为主要有三项：⽹格的正交性，雅可⽐值，扭⾓，和光滑性。

对于⼀般的CFD程序，结构化⽹格要求正交性和光滑性要⽐较好，但是对于FLUENT这样基于⾮结构⽹格的，尤其是其中程序中加⼊了很多加快收敛速度的⽅法的软件，后者要求就不要太⾼。

因此真正需要考虑⽹格影响的，⼀般应该在基于结构⽹格的软件上才需要。

基于⾮结构⽹格的有限体积法，计算通量的时候存在相邻节点的通量计算本⾝就可能存在计算误差，所以精度始终有限，顺便说⼀下，对于FLUENT，顶多⼆阶离散格式就够了，⽽且绰绰有余。

甚⾄诸多⼯程师认为⼀阶精度⾜够⽤于⼯程计算，因为FLUENT的内核算法缺陷在于，其在计算中的误差远远达不到⼆阶的精度。

⽹格质量本⾝与具体问题的具体⼏何特性、流动特性及流场求解算法有关。

因此，⽹格质量最终要由计算结果来评判，但是误差分析以及经验表明，CFD计算对计算⽹格有⼀些⼀般性的要求，例如光滑性、正交性、⽹格单元的正则性以及在流动变化剧烈的区域分布⾜够多的⽹格点等。

对于复杂⼏何外形的⽹格⽣成，这些要求往往并不可能同时完全满⾜。

例如，给定边界⽹格点分布，采⽤Laplace⽅程⽣成的⽹格是最光滑的，但是最光滑的⽹格不⼀定满⾜物⾯边界正交性条件，其⽹格点分布也很有可能不能捕捉流动特征，因此，最光滑的⽹格不⼀定是最好的⽹格。

对计算⽹格的⼀个最基本的要求当然是所有⽹格点的Jacobian必须为正值，即⽹格体积必须为正，其他⼀些最常⽤的⽹格质量度量参数包括扭⾓（skew angle）、纵横⽐（aspect ratio、Laplacian、以及弧长（arc length）等。

通过计算、检查这些参数，可以定性的甚⾄从某种程度上定量的对⽹格质量进⾏评判。

有限元网格划分的基本原则杜平安 《机械设计与制造》划分网格是建立有限元模型的一个重要环节，它要求考虑的问题较多，需要的工作量较大，所划分的网格形式对计算精度和计算规模将产生直接影响。

为建立正确、合理的有限元模型，这里介绍划分网格时应考虑的一些基本原则。

1网格数量网格数量的多少将影响计算结果的精度和计算规模的大小。

一般来讲，网格数量增加，计算精度会有所提高，但同时计算规模也会增加，所以在确定网格数量时应权衡两个因数综合考虑。

图1中的曲线1表示结构中的位移随网格数量收敛的一般曲线，曲线2代表计算时间随网格数量的变化。

可以看出，网格较少时增加网格数量可以使计算精度明显提高，而计算时间不会有大的增加。

当网格数量增加到一定程度后，再继续增加网格时精度提高甚微，而计算时间却有大幅度增加。

所以应注意增加网格的经济性。

实际应用时可以比较两种网格划分的计算结果，如果两次计算结果相差较大，可以继续增加网格，相反则停止计算。

图1位移精度和计算时间随网格数量的变化在决定网格数量时应考虑分析数据的类型。

在静力分析时，如果仅仅是计算结构的变形，网格数量可以少一些。

如果需要计算应力，则在精度要求相同的情况下应取相对较多的网格。

同样在响应计算中，计算应力响应所取的网格数应比计算位移响应多。

在计算结构固有动力特性时，若仅仅是计算少数低阶模态，可以选择较少的网格，如果计算的模态阶次较高，则应选择较多的网格。

在热分析中，结构内部的温度梯度不大，不需要大量的内部单元，这时可划分较少的网格。

2网格疏密网格疏密是指在结构不同部位采用大小不同的网格，这是为了适应计算数据的分布特点。

在计算数据变化梯度较大的部位(如应力集中处)，为了较好地反映数据变化规律，需要采用比较密集的网格。

而在计算数据变化梯度较小的部位，为减小模型规模，则应划分相对稀疏的网格。

这样，整个结构便表现出疏密不同的网格划分形式。

图2是中心带圆孔方板的四分之一模型，其网格反映了疏密不同的划分原则。

复杂网络的建模和分析复杂网络研究是当今科学领域中的热点之一，它涉及到社会、生物、物理、信息等多个领域。

复杂网络模型能够帮助我们更好地理解网络结构和演化规律。

本文主要讨论复杂网络的建模和分析方法。

一、复杂网络的基本概念复杂网络是由大量节点和连接所组成的网络，它的确切定义是一个非常复杂的问题，因此我们需要对其进行具体的描述和定义。

一般来说，复杂网络具有以下特点：1. 大规模性：复杂网络中节点数目非常庞大，通常超过数百甚至上万个。

2. 非线性性：复杂网络的演化过程存在非线性的关系，而这种非线性关系是复杂网络分析中的一个重要问题。

3. 动态性：复杂网络不断地产生新的连接，整个网络在不断地演化，形成更为复杂的结构。

4. 自相似性：复杂网络的局部结构和整体结构之间存在自相似性，即某些局部结构在整体结构中重复出现。

5. 非均质性：复杂网络中不同节点和连接的权重、度数、邻居数等参数都存在一定程度的不均质性。

基于以上特点，我们可以将复杂网络建模成为一个包含大量节点和连接的网络结构，通过分析网络的演化过程以及节点和连接之间的关系，来研究其运作机制和规律。

二、复杂网络的建模方法为了研究复杂网络的特性和演化过程，需要对其进行建模。

复杂网络的建模方法主要可以分为两类：统计模型和物理模型。

1. 统计模型统计模型是利用大量的数据进行拟合，而得到的数学模型。

统计模型通常把复杂网络建模成一个随机图，其中节点、连边、度数等概率都是随机的。

根据这些概率可以推出整个网络的拓扑结构。

统计模型中比较常见的是随机图模型和小世界模型。

随机图模型是一种最简单的复杂网络模型，该模型中所有节点的度分布都是相同的，没有统计规律可言。

随机图模型不仅适合描述现实中的网络，而且可以作为一种基准，评估现实中复杂网络的性质和特点。

相比随机图模型，小世界模型更加符合现实中复杂网络的分布规律。

小世界模型主要基于「小世界效应」，即复杂网络中任意两个节点之间距离较短，由少数中心节点所控制。

CFD网格及其生成方法概述作者：王福军网格是CFD模型的几何表达形式，也是模拟与分析的载体。

网格质量对CFD计算精度和计算效率有重要影响。

对于复杂的CFD问题，网格生成极为耗时，且极易出错，生成网格所需时间常常大于实际CFD计算的时间。

因此，有必要对网格生成方式给以足够的关注。

1 网格类型网格（grid）分为结构网格和非结构网格两大类。

结构网格即网格中节点排列有序、邻点间的关系明确，如图1所示。

对一于复杂的儿何区域，结构网格是分块构造的，这就形成了块结构网格（block-structured grids）。

图2是块结构网格实例。

图1 结构网格实例图2 块结构网格实例与结构网格不同，在非结构网格（unstructured grid）中，节点的位置无法用一个固定的法则予以有序地命名。

图3是非结构网格示例。

这种网格虽然生成过程比较复杂，但却有着极好的适应性，尤其对具有复杂边界的流场计算问题特别有效。

非结构网格一般通过专门的程序或软件来生成。

图3 非结构网格实例2 网格单元的分类单元（cell）是构成网格的基本元素。

在结构网格中，常用的ZD网格单元是四边形单元，3D网格单元是六面体单元。

而在非结构网格中，常用的2D网格单元还有三角形单元，3D 网格单元还有四面体单元和五面体单元，其中五面体单元还可分为棱锥形（或楔形）和金字塔形单元等。

图4和图5分别示出了常用的2D和3D网格单元。

图4 常用的2D网格单元图5 常用的3D网格单元3 单连域与多连域网格网格区域（cell zone）分为单连域和多连域两类。

所谓单连域是指求解区域边界线内不包含有非求解区域的情形。

单连域内的任何封闭曲线都能连续地收缩至点而不越过其边界。

如果在求解区域内包含有非求解区域，则称该求解区域为多连域。

所有的绕流流动，都属于典型的多连域问题，如机翼的绕流，水轮机或水泵内单个叶片或一组叶片的绕流等。

图2及图3均是多连域的例子。

对于绕流问题的多连域内的网格，有O型和C型两种。

划分网格是建立有限元模型的一个重要环节，它要求考虑的问题较多，需要的工作量较大，所划分的网格形式对计算精度和计算规模将产生直接影响。

为建立正确、合理的有限元模型，这里介绍划分网格时应考虑的一些基本原则。

1网格数量网格数量的多少将影响计算结果的精度和计算规模的大小。

一般来讲，网格数量增加，计算精度会有所提高，但同时计算规模也会增加，所以在确定网格数量时应权衡两个因数综合考虑。

图1中的曲线1表示结构中的位移随网格数量收敛的一般曲线，曲线2代表计算时间随网格数量的变化。

可以看出，网格较少时增加网格数量可以使计算精度明显提高，而计算时间不会有大的增加。

当网格数量增加到一定程度后，再继续增加网格时精度提高甚微，而计算时间却有大幅度增加。

所以应注意增加网格的经济性。

实际应用时可以比较两种网格划分的计算结果，如果两次计算结果相差较大，可以继续增加网格，相反则停止计算。

图1位移精度和计算时间随网格数量的变化在决定网格数量时应考虑分析数据的类型。

在静力分析时，如果仅仅是计算结构的变形，网格数量可以少一些。

如果需要计算应力，则在精度要求相同的情况下应取相对较多的网格。

同样在响应计算中，计算应力响应所取的网格数应比计算位移响应多。

在计算结构固有动力特性时，若仅仅是计算少数低阶模态，可以选择较少的网格，如果计算的模态阶次较高，则应选择较多的网格。

在热分析中，结构内部的温度梯度不大，不需要大量的内部单元，这时可划分较少的网格。

2网格疏密网格疏密是指在结构不同部位采用大小不同的网格，这是为了适应计算数据的分布特点。

在计算数据变化梯度较大的部位(如应力集中处)，为了较好地反映数据变化规律，需要采用比较密集的网格。

而在计算数据变化梯度较小的部位，为减小模型规模，则应划分相对稀疏的网格。

这样，整个结构便表现出疏密不同的网格划分形式。

图2是中心带圆孔方板的四分之一模型，其网格反映了疏密不同的划分原则。

小圆孔附近存在应力集中，采用了比较密的网格。

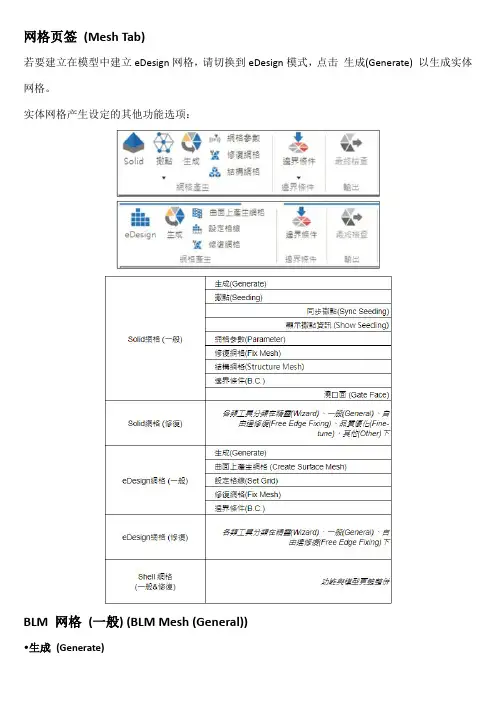
网格页签(Mesh Tab)若要建立在模型中建立eDesign网格，请切换到eDesign模式，点击生成(Generate) 以生成实体网格。

实体网格产生设定的其他功能选项：BLM 网格(一般) (BLM Mesh (General))•生成(Generate)点击生成，使用者可生成塑件、流道、塑件嵌件、水路、模座嵌件和模座的表面网格与实体网格，点选生成启动网格工具区，点击网格工具区内的生成开始生成自动网格，网格生成主流程包括：(1) 表面网格；(2) 实体网格；(3) 冷却系统的表面实体网格，并依各部位(例如嵌件、模座、流道) 再细分。

手动设立网格生成中止点可透过点击欲中止网格生成的项目，使其项目前面出现图钉的图标，流程跑完停止点会停下，再度运行则会接续流程。

当采用连续生成网格流程，因事件发生导致流程中止时会在该项目前面显示惊叹号图标，点选确认可继续生成网格。

当网格生成中断时，对话窗口会跳出显示警告讯息与建议方案。

1. 当网格生成失败，该问题项目前面出现惊叹号；2. 警告讯息与建议方案跳出；3. 手动设定中止点(图钉图示)•浇口网格重建(Gate Rebuild)当生成流道的实体网格时，Moldex3D会同时重建并加密塑件在进浇位置的实体网格，来确保塑件与流道/浇口间的网格品质及接合。

但当浇口网格重建失败时，会多显示一种BC类型：浇口面(Gate Face)，来让使用者利用编辑工具边界条件(Boundary Condition) 来增减BC调整接合区域。

塑件与嵌件交界面的网格匹配可能会由于浇口网格重建而再度错位。

如果要维持浇口网格重建后的匹配网格，请在偏好设定中开启重建浇口区域时保留匹配网格(可能要同时关闭允许非匹配网格来让设定生效)。

•修改撒点(BLM Seeding)点击Seeding，根据初始网格大小与节点分布的非等值类型来手动调整网格节点。

•点击Seeding后，程序会依据模型的肉厚开始预测网格建议大小。

一些需要了解的关于CFD的常识关于网格：1. 网格是CFD 的几何表达形式，也是模拟和分析的载体。

2. 网格质量对CFD 计算的精度和效率影响很大。

3. 单连域：求解区域边界线内不包含有非求解区域。

多连域：求解区域含有非求解区域。

4. 绕流问题的网格一般为O 型和C 型网格。

考虑使用结构还是非结构网格的时候，主要考虑以下几个因素：1. 主要考虑网格的多少，这才是真正影响计算消耗最大的因素。

主要从以下的观点进行考虑。

当几何外形太复杂或者流动的长度尺度太大时，三角形网格和四面体网格所生成的单元会比等量的包含四边形网格和六面体网格的单元少得多。

这是因为三角形网格和四面体网格允许单元聚集在流域的所选区域，而四边形网格和六面体网格会在不需要加密的地方产生单元。

非结构的四边形网格和六面体网格为对于一般复杂外形提供了许多三角形和四面体网格的优点。

（复杂外形建议用非结构网格）2. 网格的比率。

四边形和六边形单元的一个特点就是它们在某些情况下可以允许比三角形/四面体单元更大的比率。

三角形/四面体单元的大比率总会影响单元的歪斜。

因此，如果你有相对简单的几何外形，而且流动和几何外形很符合，比如长管，你就可以使用大比率的四边形和六边形单元。

这种网格可能会比三角形/四面体网格少很多单元。

（流动和外形比较符合且外形简单时，建议使用结构网格）关于数值耗散问题，有如下几点：● 当真实耗散很小时，即对流占主导地位时，数值耗散是显而易见的。

● 所有的解决流体问题的数值格式都会有数值耗散，这是因为数值耗散来源于截断误差，截断误差是描述流体流动的离散方程导致的。

●FLUENT 中所用的二阶离散格式可以帮助减少解的数值耗散的影响。

● 数值耗散量的大小与网格的分辨率成反比。

因此解决数值耗散问题的一个方法就是精化网格。

● 当流动和网格成一条直线时数值耗散最小（所以我们才要使用结构网格来计算啊）最后一点和网格选择最有关系。

很明显，使用三角形/四面体网格流动永远不会和网格成一条直线，而如果几何外形不是很复杂时，四边形网格和六面体网格可能就会实现流动和网格成一条线。

Байду номын сангаас
第二章 规划分析方案 2.1 规划的重要性 当开始建模时，用户将（有意地或无意地）作许多决定以确定如何来对物理系统进行数值模 拟；分析的目标是什么？模型是全部或仅是物理系统的部分？模型将包含多少细节？选用什 么样的单元？有限元网格用多大的密度？总之，你将对要回答的问题的计算费用（CPU 时 间等）及结果的精度进行平衡考虑。你在规划阶段作出的这些决定将大体上控制你分析的成 功与否。 2.2 确定分析目标 确定分析目标的工作与 ANSYS 程序的功能无关，完全取决于用户的知识、经验及职业技能， 只有用户才能确定自己的分析目标，开始时建立的目标将影响用户生成模型时的其它选择。 2.3 选择模型类型（二维、三维等） 有限元模型可分为二维和三维两种。可以由点单元、线单元、面单元或实体单元组成，当然， 也可以将不同类型的单元混合使用（注意要保证自由度的相容性）。例如，带筋的薄壳结构 可用三维壳单元离散蒙皮，用三维梁单元来离散蒙皮下的筋。对模型的尺寸和单元类型的选 择也就决定生成模型的方法。 线模型代表二维和三维梁或管结构，及三维轴对称壳结构的二维模型。实体建模通常不便于 生成线模型，而通常由直接生成方法创建。 二维实体模型在薄平板结构（平面应力），等截面的“无限长”结构（平面应变）或轴对称实 体结构。尽管许多二维分析模型用直接生成方法并不困难，但通常用实体建模更容易。 三维壳模型用于描述三维空间中的薄壁结构，尽管某些三维壳模型用直接生成方法创建并不 困难，但用实体建模方法通常会更容易。 三维实体分析模型用于描述三维空间中截面积不等，也不是轴对称的厚结构。用直接生成的 方法建立三维实体模型较复杂，实体建模会使其变得容易些。 2.4 线性和高次单元的选择 ANSYS 程序的单元库包括两种基本类型的面和体单元：线性单元（有或无特殊形状的）和 二次单元。这些基本单元类型如图 2-1 所示，下面来探讨这两种基本类型单元的选择。

常用 mesh law 节点分布规律Mesh Law是一种节点分布规律，它是计算机科学和电信工程领域中常用的一种网格生成方法。

在3D模型建模、有限元分析和计算机图形学等应用中经常使用Mesh Law来生成规则和紧密的网格。

Mesh Law节点分布规律的核心思想是根据几何形状的特性和研究目标的要求，在保持节点分布均匀性的同时，尽可能地减少节点数目。

Mesh Law方法根据要求的精度和计算效率的需求，可以选择不同的节点分布策略。

常用的Mesh Law节点分布规律包括等距分布、等面积分布、等角分布、三角形状分布和四边形状分布等。

1.等距分布：等距分布是指节点间的距离相等，即每个节点之间的间距都相同。

这种分布方法适用于对形状要求不高的场景，如空间网格划分和地图网格生成等。

2.等面积分布：等面积分布是指每个节点所占的面积相等。

在进行精细网格划分时，等面积分布可以保证各个区域的节点数量基本相同，从而减小误差。

3.等角分布：等角分布是指每个节点之间的角度相等。

等角分布方法通常用于生成正多边形网格，如六边形网格，其具有均匀性好、紧密度高的特点。

4.三角形状分布：三角形状分布是指节点按照三角形的形状呈现规律地分布。

这种分布方法适用于规则形状和对精度要求较高的场景，如模拟流体动力学和计算机图形学中的三角网格生成。

5.四边形状分布：四边形状分布是指节点按照四边形的形状呈现规律地分布。

与三角形分布相比，四边形分布具有更好的可调性和网格生成效率，特别适用于有限元分析和机械工程领域。

Mesh Law节点分布规律的选择应根据具体的应用场景和要求来确定。

在实际应用中，通常会根据形状复杂度、计算资源和精度要求等因素进行综合考虑。

同时，网格生成的算法和工具的选择也会对节点分布规律产生影响。

总之，Mesh Law节点分布规律通过合理地规划节点的位置和分布，可以实现高效的网格生成和计算，从而在各个领域中发挥作用。

随着计算机科学和电信工程领域的发展，对节点分布规律的研究和创新也在不断进行，以满足实际应用的需求。

一、前言有限元网格划分是进行有限元数值模拟分析至关重要的一步，它直接影响着后续数值汁算分析结果的精确性。

网格划分涉及单元的形状及英拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素。

从几何表达上讲，梁和杆是相同的，从物理和数值求解上讲则是有区别的。

同理，平而应力和平面应变情况设计的单元求解方程也不相同。

在有限元数值求解中，单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成，连续体单元以及壳、板、梁单元的而内均采用高斯（Gauss）积分，而壳、板、梁单元的厚度方向采用辛普生（Simpson）积分。

辛普生积分点的间隔是一泄的，沿厚度分成奇数积分点。

由于不同单元的刚度矩阵不同，采用数值积分的求解方式不同，因此实际应用中，一定要采用合理的单元来模拟求解。

CAD软件中流行的实体建模包括基于特征的参数化建模和空间自由曲而混合造型两种方法。

Pro/E和SoildWorks是特征参数化造型的代表，而CATIA与Unigraphics等则将特征参数化和空间自由曲面混合造型有机的结合起来。

现有CAD软件对表而形态的表示法已经大大超过了CAE 软件，因此，在将CAD实体模型导入CAE软件的过程中，必须将CAD 模型中苴他表示法的表面形态转换到CAE软件的表示法上，转换精度的髙低取决于接口程序的好坏。

在转换过程中，程序需要解决好几何图形（曲线与曲而的空间位苣）和拓扑关系（各图形数据的逻借关系）两个关键问题。

英中几何图形的传递相对容易实现，而图形间的拓扑关系容易岀现传递失败的情况。

数据传递而临的一个重大挑战是，将导入CAE程序的CAD模型改造成适合有限元分析的网格模型。

在很多情况下，导入CAE程序的模型可能包含许多设计细节，如细小的孔、狭窄的槽，甚至是建模过程中形成的小曲而等。

这些细肖往往不是基于结构的考虑，保留这些细肖，单元数量势必增加，甚至会掩盖问题的主要矛盾，对分析结果造成负而影响。

CAD模型的“完整性”问题是困扰网格剖分的障碍之一。

Moldflow网格划分及修复 Moldflow网格划分及修复
有限元法原理 Moldflow中将这些单元称为 Moldflow中将这些单元称为Mesh（网格） 中将这些单元称为Mesh（网格） 网格是整个数值计算的基础，所以网格划分十分重要。 网格是整个数值计算的基础，所以网格划分十分重要。
网格的三种类型
1、中面网格（Midplane）
中面网格有三节点的三角形单元组成， 中面网格有三节点的三角形单元组成，网格创建在 模型壁厚中间处，形成单层网格。 模型壁厚中间处，形成单层网格。在创建网格过程中要 实时提取模型的壁厚信息，并赋予相应的三角形单元。 实时提取模型的壁厚信息，并赋予相应的三角形单元。 中面网格优点为分析速度快，效率高， 中面网格优点为分析速度快，效率高，适用于薄壳 类零件。 类零件。
• 自由边粘合
• 平滑节点：将与选定节点有关联的单元进行重新划分网格， 平滑节点：将与选定节点有关联的单元进行重新划分网格， 目的是得到更加均匀的网格分布，以便于计算。 目的是得到更加均匀的网格分布，以便于计算。
• 创建一维单元（Crate beams):通过存在两节点来创建一维 创建一维单元（ 通过存在两节点来创建一维 单元（一维单元在冷却系统、浇注系统中广泛使用）。 单元（一维单元在冷却系统、浇注系统中广泛使用）。 • 分别在对话框中输入创建一维单元的两个节点既可
• 采用Display显示诊断结果，系统将用不同颜色的引出线指出 纵横比大小不同的单元。单击引出线，可选中存在纵横比缺 陷单元。
• 采用 采用Text方式，Moldflow将诊断结果以文本的方式在对话 方式， 方式 将诊断结果以文本的方式在对话 框中给出。 框中给出。
• 重叠单元诊断（Overlapping Elements diagnostic) 重叠单元诊断（ 如下图所示

度，如下图4。
2D网格划分技巧:
a b c
图4

a图中单元的类型为“MIXED”，算法为“free”；b、c图中单元的类型为“QUADS”，b 图中的算法为“free”，c图中的算法为“pentagon”。
在日常的网格划分工作中，选择合适的单元类型及算法，可提高分网速度及质量。
D网格划分技巧:
抽中面:
对于有限元分析,很多薄壁部件用壳单元表示； 厚度用数值来表示, 而不是几何形状； 网格通常放在部件的中面上； Midsurface 在中间平面位置生成一个面 网格直接划分在该面上； 用Geom的Midsurface面板生成中面 : Auto Midsurface ；
几何拓扑关系:
自定义快捷操作：Preferences-Keyboard Settings。
软件界面:
菜单栏
模型树区域
工具栏
图形显示区
页面菜单
标题信息栏
面板菜单
软件界面_页面菜单
包含与创建和编辑几何模型有关的功能； 包含一维单元的创建和编辑功能； 包含二维单元的创建和编辑功能； 包含三维单元的创建和编辑功能； 包含分析问题以及边界条件定义的功能； 包含模型质量检查以及有关模型信息的功能； 包含后处理和绘制曲线图的功能。
优化拓扑关系：就是优化面与面之间的连接关系，修复错误的几何关系，还原几何数据到 部件的实际状态，并为后续的几何清理做铺垫。如下图示意。
重复曲面 删除
缺失曲面 创建
自由边（对） 合并
几何清理目的:
简化几何特征，改善几何模型的拓扑关系，以获得高质量的网格。 CAD模型需要精确的几何表述，通常包含某些细微特征，如小倒角、小孔等；而有 限元分析时，若要准确模拟这些特征，需要用到很小的单元，导致求解成本急剧升高， 通常将这些无关大局的特征简化处理。此外，在导入几何模型时，有些几何信息会出现 丢失、错位等现象，如不进行几何清理，将导致求解精度变差。因此改正导入模型时出 现的错误，消除不必要的结合特征对提高网格质量及求解精度是很重要的一个环节。

网格运行机制网格运行机制是一种应用可扩展性的网络技术，它将来自不同位置的计算机连接在一起，以协同完成大规模的计算任务。

这种技术的核心是对节点进行分布式计算，以使节点之间共享信息。

它可以将复杂的计算任务分解成多个小块，每个小块分发到不同的节点上进行计算，最后将多个小块的结果组合起来，从而得出最终结果。

网格运行机制可以将计算机分布在不同的地方，这样就可以在不同的节点上进行数据的共享和计算。

它可以用来进行大规模计算，比如模拟数值计算，处理和存储大量的数据，进行科研计算和应用计算，以及进行遥测监控和多用户协同编辑等任务。

它可以极大地提高计算效率，并节省计算机硬件成本。

网格运行机制的工作原理包括三个基本步骤：节点发现，节点调度和节点失效。

首先，网格运行机制会发现可用的节点；其次，根据应用需求，它会调度不同节点上的计算任务，使不同节点之间可以有效地进行数据共享和任务协调；最后，在网格运行机制确定节点失效之后，它会调用备份机制，分配任务给其他可用的节点，确保网络的可靠性和高效率。

网格运行机制的实施有多种方式。

如果使用分布式计算模型，可以将应用程序拆分成多个子任务，并分发到不同的节点执行，最后读取和组装子任务的结果，从而得出更准确的结果。

另一种方式是分布式文件系统，其中的文件可以在不同的节点上存储，从而实现数据的共享，同时可以实现多用户的协同编辑。

网格运行机制可以加快大规模计算的效率，但也存在一些挑战。

首先，在节点间传输数据的过程中可能受到网络延迟的影响；其次，如果部分节点出现故障，网络可能会受到影响；最后，节点上的运行环境可能不同，因此可能会影响计算精度。

为了解决这些挑战，可以采用一些技术，如虚拟环境（Virtual Environment）、数据同步技术（Data Synchronization）和失效节点管理机制（Fault Node Management）等。

网格运行机制是一项强大而有效的网络技术，可以帮助我们分担大规模计算的负担，提高计算效率，节省硬件成本，同时实现数据的共享和任务的协同。