分配问题与匈牙利法说课讲解
- 格式:ppt
- 大小:457.00 KB
- 文档页数:31

【算法题】任务分配问题---匈⽛利算法⼀、问题描述问题描述:N个⼈分配N项任务,⼀个⼈只能分配⼀项任务,⼀项任务只能分配给⼀个⼈,将⼀项任务分配给⼀个⼈是需要⽀付报酬,如何分配任务,保证⽀付的报酬总数最⼩。
问题数学描述:⼆、实例分析---穷举法在讲将匈⽛利算法解决任务问题之前,先分析⼏个具体实例。
以3个⼯作⼈员和3项任务为实例,下图为薪酬图表和根据薪酬图表所得的cost矩阵。
利⽤最简单的⽅法(穷举法)进⾏求解,计算出所有分配情况的总薪酬开销,然后求最⼩值。
total_cost1 = 250 + 600 + 250 = 1100; x00 = 1,x11 = 1,x22 = 1;total_cost2 = 250 + 350 + 400 = 1000; x00 = 1,x12 = 1,x21 = 1;total_cost3 = 400 + 400 + 250 = 1050; x01 = 1,x10 = 1,x22 = 1;total_cost4 = 400 + 350 + 200 = 950; x01 = 1,x12 = 1,x20 = 1; //最优分配total_cost5 = 350 + 400 + 400 = 1150; x02 = 1,x10 = 1,x21 = 1;total_cost6 = 350 + 600 + 250 = 1150; x02 = 1,x11 = 1,x22 = 1;对于任务数和⼈员数较少时,可利⽤穷举法计算结果。
若将N任务分配给N个⼈员,其包含的所有分配情况数⽬为N!,N增⼤时,穷举法将难以完成任务。
三、匈⽛利算法下⾯简要介绍匈⽛利算法。
其基本的理论基础是针对cost矩阵,将cost矩阵的⼀⾏或⼀列数据加上或减去⼀个数,其最优任务分配求解问题不变。
算法的基本步骤如下:四、实例分析---匈⽛利算法下⾯结合具体实例,分析匈⽛利算法如何解决任务分配问题。
以N = 4为实例,下图为cost列表和cost矩阵。



运筹学课程设计指派问题的匈牙利法专业:姓名:学号:1.算法思想:匈牙利算法的基本思想是修改效益矩阵的行或列,使得每一行或列中至少有一个为零的元素,经过修正后,直至在不同行、不同列中至少有一个零元素,从而得到与这些零元素相对应的一个完全分配方案。
当它用于效益矩阵时,这个完全分配方案就是一个最优分配,它使总的效益为最小。
这种方法总是在有限步內收敛于一个最优解。
该方法的理论基础是:在效益矩阵的任何行或列中,加上或减去一个常数后不会改变最优分配。
2.算法流程或步骤:1.将原始效益矩阵C的每行、每列各元素都依次减去该行、该列的最小元素,使每行、每列都至少出现一个0元素,以构成等价的效益矩阵C’。
2.圈0元素。
在C’中未被直线通过的含0元素最少的行(或列)中圈出一个0元素,通过这个0元素作一条竖(或横)线。
重复此步,若这样能圈出不同行不同列的n个0元素,转第四步,否则转第三步。
3.调整效益矩阵。
在C’中未被直线穿过的数集D中,找出最小的数d,D中所有数都减去d,C’中两条直线相交处的数都加的d。
去掉直线,组成新的等价效益矩阵仍叫C’,返回第二步。
X=0,这就是一种最优分配。
最低总4.令被圈0元素对应位置的X ij=1,其余ij耗费是C中使X=1的各位置上各元素的和。
ij算法流程图:3.算法源程序:#include<iostream.h>typedef struct matrix{float cost[101][101];int zeroelem[101][101];float costforout[101][101];int matrixsize;int personnumber;int jobnumber;}matrix;matrix sb;int result[501][2];void twozero(matrix &sb);void judge(matrix &sb,int result[501][2]);void refresh(matrix &sb);void circlezero(matrix &sb);matrix input();void output(int result[501][2],matrix sb);void zeroout(matrix &sb);matrix input(){matrix sb;int m;int pnumber,jnumber;int i,j;float k;char w;cout<<"指派问题的匈牙利解法:"<<endl;cout<<"求最大值,请输入1;求最小值,请输入0:"<<endl;cin>>m;while(m!=1&&m!=0){cout<<"请输入1或0:"<<endl;cin>>m;}cout<<"请输入人数(人数介于1和100之间):"<<endl;cin>>pnumber;while(pnumber<1||pnumber>100){cout<<"请输入合法数据:"<<endl;cin>>pnumber;}cout<<"请输入工作数(介于1和100之间):"<<endl;cin>>jnumber;while(jnumber<1||jnumber>100){cout<<"请输入合法数据:"<<endl;cin>>jnumber;}cout<<"请输入"<<pnumber<<"行"<<jnumber<<"列的矩阵,同一行内以空格间隔,不同行间以回车分隔,以$结束输入:\n";for(i=1;i<=pnumber;i++)for(j=1;j<=jnumber;j++){cin>>sb.cost[i][j];sb.costforout[i][j]=sb.cost[i][j];}cin>>w;if(jnumber>pnumber)for(i=pnumber+1;i<=jnumber;i++)for(j=1;j<=jnumber;j++){sb.cost[i][j]=0;sb.costforout[i][j]=0;}else{if(pnumber>jnumber)for(i=1;i<=pnumber;i++)for(j=jnumber+1;j<=pnumber;j++){sb.cost[i][j]=0;sb.costforout[i][j]=0;}}sb.matrixsize=pnumber;if(pnumber<jnumber)sb.matrixsize=jnumber;sb.personnumber=pnumber;sb.jobnumber=jnumber;if(m==1){k=0;for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)if(sb.cost[i][j]>k)k=sb.cost[i][j];for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)sb.cost[i][j]=k-sb.cost[i][j];}return sb;}void circlezero(matrix &sb){int i,j;float k;int p;for(i=0;i<=sb.matrixsize;i++)sb.cost[i][0]=0;for(j=1;j<=sb.matrixsize;j++)sb.cost[0][j]=0;for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)if(sb.cost[i][j]==0){sb.cost[i][0]++;sb.cost[0][j]++;sb.cost[0][0]++;}for(i=0;i<=sb.matrixsize;i++)for(j=0;j<=sb.matrixsize;j++)sb.zeroelem[i][j]=0;k=sb.cost[0][0]+1;while(sb.cost[0][0]<k){k=sb.cost[0][0];for(i=1;i<=sb.matrixsize;i++){if(sb.cost[i][0]==1){for(j=1;j<=sb.matrixsize;j++)if(sb.cost[i][j]==0&&sb.zeroelem[i][j]==0)break;sb.zeroelem[i][j]=1;sb.cost[i][0]--;sb.cost[0][j]--;sb.cost[0][0]--;if(sb.cost[0][j]>0)for(p=1;p<=sb.matrixsize;p++)if(sb.cost[p][j]==0&&sb.zeroelem[p][j]==0){sb.zeroelem[p][j]=2;sb.cost[p][0]--;sb.cost[0][j]--;sb.cost[0][0]--;}}}for(j=1;j<=sb.matrixsize;j++){if(sb.cost[0][j]==1){for(i=1;i<=sb.matrixsize;i++)if(sb.cost[i][j]==0&&sb.zeroelem[i][j]==0)break;sb.zeroelem[i][j]=1;sb.cost[i][0]--;sb.cost[0][j]--;sb.cost[0][0]--;if(sb.cost[i][0]>0)for(p=1;p<=sb.matrixsize;p++)if(sb.cost[i][p]==0&&sb.zeroelem[i][p]==0){sb.zeroelem[i][p]=2;sb.cost[i][0]--;sb.cost[0][p]--;sb.cost[0][0]--;}}}}if(sb.cost[0][0]>0)twozero(sb);elsejudge(sb,result);}void twozero(matrix &sb){int i,j;int p,q;int m,n;float k;matrix st;for(i=1;i<=sb.matrixsize;i++)if(sb.cost[i][0]>0)break;if(i<=sb.matrixsize){for(j=1;j<=sb.matrixsize;j++){st=sb;if(sb.cost[i][j]==0&&sb.zeroelem[i][j]==0){sb.zeroelem[i][j]=1;sb.cost[i][0]--;sb.cost[0][j]--;sb.cost[0][0]--;for(q=1;q<=sb.matrixsize;q++)if(sb.cost[i][q]==0&&sb.zeroelem[i][q]==0){sb.zeroelem[i][q]=2;sb.cost[i][0]--;sb.cost[0][q]--;sb.cost[0][0]--;}for(p=1;p<=sb.matrixsize;p++)if(sb.cost[p][j]==0&&sb.zeroelem[p][j]==0){sb.zeroelem[p][j]=2;sb.cost[p][0]--;sb.cost[0][j]--;sb.cost[0][0]--;}k=sb.cost[0][0]+1;while(sb.cost[0][0]<k){k=sb.cost[0][0];for(p=i+1;p<=sb.matrixsize;p++){if(sb.cost[p][0]==1){for(q=1;q<=sb.matrixsize;q++)if(sb.cost[p][q]==0&&sb.zeroelem[p][q]==0)break;sb.zeroelem[p][q]=1;sb.cost[p][0]--;sb.cost[0][q]--;sb.cost[0][0]--;for(m=1;m<=sb.matrixsize;m++)if(sb.cost[m][q]=0&&sb.zeroelem[m][q]==0){sb.zeroelem[m][q]=2;sb.cost[m][0]--;sb.cost[0][q]--;sb.cost[0][0]--;}}}for(q=1;q<=sb.matrixsize;q++){if(sb.cost[0][q]==1){for(p=1;p<=sb.matrixsize;p++)if(sb.cost[p][q]==0&&sb.zeroelem[p][q]==0)break;sb.zeroelem[p][q]=1;sb.cost[p][q]--;sb.cost[0][q]--;sb.cost[0][0]--;for(n=1;n<=sb.matrixsize;n++)if(sb.cost[p][n]==0&&sb.zeroelem[p][n]==0){sb.zeroelem[p][n]=2;sb.cost[p][0]--;sb.cost[0][n]--;sb.cost[0][0]--;}}}}if(sb.cost[0][0]>0)twozero(sb);elsejudge(sb,result);}sb=st;}}}void judge(matrix &sb,int result[501][2]){int i,j;int m;int n;int k;m=0;for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==1)m++;if(m==sb.matrixsize){k=1;for(n=1;n<=result[0][0];n++){for(i=1;i<=sb.matrixsize;i++){for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==1)break;if(i<=sb.personnumber&&j<=sb.jobnumber)if(j!=result[k][1])break;k++;}if(i==sb.matrixsize+1)break;elsek=n*sb.matrixsize+1;}if(n>result[0][0]){k=result[0][0]*sb.matrixsize+1;for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==1){result[k][0]=i;result[k++][1]=j;}result[0][0]++;}}else{refresh(sb);}}void refresh(matrix &sb){int i,j;float k;int p;k=0;for(i=1;i<=sb.matrixsize;i++){for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==1){sb.zeroelem[i][0]=1;break;}}while(k==0){k=1;for(i=1;i<=sb.matrixsize;i++)if(sb.zeroelem[i][0]==0){sb.zeroelem[i][0]=2;for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==2){sb.zeroelem[0][j]=1;}}for(j=1;j<=sb.matrixsize;j++){if(sb.zeroelem[0][j]==1){sb.zeroelem[0][j]=2;for(i=1;i<=sb.matrixsize;i++)if(sb.zeroelem[i][j]==1){sb.zeroelem[i][0]=0;k=0;}}}}p=0;k=0;for(i=1;i<=sb.matrixsize;i++){if(sb.zeroelem[i][0]==2){for(j=1;j<=sb.matrixsize;j++){if(sb.zeroelem[0][j]!=2)if(p==0){k=sb.cost[i][j];p=1;}else{if(sb.cost[i][j]<k)k=sb.cost[i][j];}}}}for(i=1;i<=sb.matrixsize;i++){if(sb.zeroelem[i][0]==2)for(j=1;j<=sb.matrixsize;j++)sb.cost[i][j]=sb.cost[i][j]-k;}for(j=1;j<=sb.matrixsize;j++){if(sb.zeroelem[0][j]==2)for(i=1;i<=sb.matrixsize;i++)sb.cost[i][j]=sb.cost[i][j]+k;}for(i=0;i<=sb.matrixsize;i++)for(j=0;j<=sb.matrixsize;j++)sb.zeroelem[i][j]=0;circlezero(sb);}void zeroout(matrix &sb){int i,j;float k;for(i=1;i<=sb.matrixsize;i++){k=sb.cost[i][1];for(j=2;j<=sb.matrixsize;j++)if(sb.cost[i][j]<k)k=sb.cost[i][j];for(j=1;j<=sb.matrixsize;j++)sb.cost[i][j]=sb.cost[i][j]-k;}for(j=1;j<=sb.matrixsize;j++){k=sb.cost[1][j];for(i=2;i<=sb.matrixsize;i++)if(sb.cost[i][j]<k)k=sb.cost[i][j];for(i=1;i<=sb.matrixsize;i++)sb.cost[i][j]=sb.cost[i][j]-k;}}void output(int result[501][2],matrix sb) {int k;int i;int j;int p;char w;float v;v=0;for(i=1;i<=sb.matrixsize;i++){v=v+sb.costforout[i][result[i][1]];}cout<<"最优解的目标函数值为"<<v;k=result[0][0];if(k>5){cout<<"解的个数超过了限制."<<endl;k=5;}for(i=1;i<=k;i++){cout<<"输入任意字符后输出第"<<i<<"种解."<<endl;cin>>w;p=(i-1)*sb.matrixsize+1;for(j=p;j<p+sb.matrixsize;j++)if(result[j][0]<=sb.personnumber&&result[j][1]<=sb.jobnumber)cout<<"第"<<result[j][0]<<"个人做第"<<result[j][1]<<"件工作."<<endl;}}void main(){result[0][0]=0;sb=input();zeroout(sb);circlezero(sb);output(result,sb);}4. 算例和结果:自己运算结果为:->⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡3302102512010321->⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡330110241200032034526635546967562543----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡可以看出:第1人做第4件工作;第2人做第1件工作;第3人做第3件工作;第4人做第2件工作。
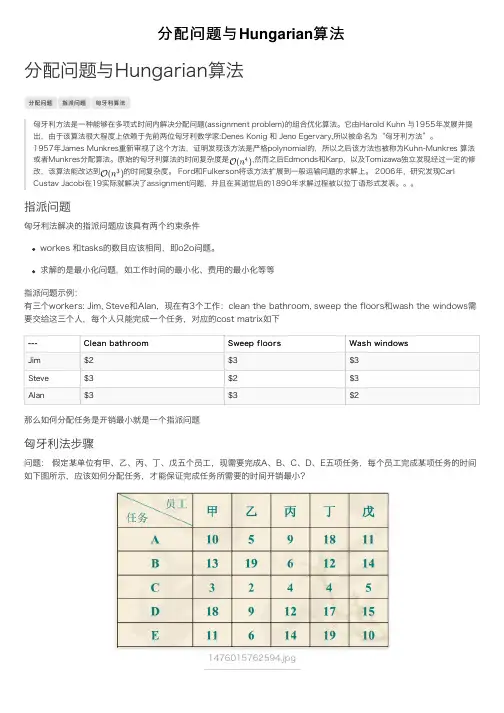
分配问题与Hungarian算法分配问题与Hungarian算法分配问题指派问题匈⽛利算法匈⽛利⽅法是⼀种能够在多项式时间内解决分配问题(assignment problem)的组合优化算法。
它由Harold Kuhn 与1955年发展并提出,由于该算法很⼤程度上依赖于先前两位匈⽛利数学家:Denes Konig 和 Jeno Egervary,所以被命名为“匈⽛利⽅法”。
1957年James Munkres重新审视了这个⽅法,证明发现该⽅法是严格polynomial的,所以之后该⽅法也被称为Kuhn-Munkres 算法或者Munkres分配算法。
原始的匈⽛利算法的时间复杂度是,然⽽之后Edmonds和Karp,以及Tomizawa独⽴发现经过⼀定的修改,该算法能改达到的时间复杂度。
Ford和Fulkerson将该⽅法扩展到⼀般运输问题的求解上。
2006年,研究发现Carl Custav Jacobi在19实际就解决了assignment问题,并且在其逝世后的1890年求解过程被以拉丁语形式发表。
指派问题匈⽛利法解决的指派问题应该具有两个约束条件workes 和tasks的数⽬应该相同,即o2o问题。
求解的是最⼩化问题,如⼯作时间的最⼩化、费⽤的最⼩化等等指派问题⽰例:有三个workers: Jim, Steve和Alan,现在有3个⼯作:clean the bathroom, sweep the floors和wash the windows需要交给这三个⼈,每个⼈只能完成⼀个任务,对应的cost matrix如下---Clean bathroom Sweep floors Wash windowsJim$2$3$3Steve$3$2$3Alan$3$3$2那么如何分配任务是开销最⼩就是⼀个指派问题匈⽛利法步骤问题: 假定某单位有甲、⼄、丙、丁、戊五个员⼯,现需要完成A、B、C、D、E五项任务,每个员⼯完成某项任务的时间如下图所⽰,应该如何分配任务,才能保证完成任务所需要的时间开销最⼩?1476015762594.jpg解:1. 写出系数矩阵2. 更新系数矩阵,使系数矩阵的每⼀⾏每⼀列都减去该⾏该列的最⼩值,保证每⼀⾏每⼀列都有0元素出现,参见定理2.3. 选择只有⼀个0元素的⾏或列将该0元素标注为独⽴0元素,并将该0元素所在的列或⾏中0元素划掉,直⾄找不到满⾜条件的⾏或列,需要注意的是在循环时,划掉的0元素不再视为0元素。