匈牙利算法示例
- 格式:ppt
- 大小:263.50 KB
- 文档页数:25


3.2 求解指派问题的匈牙利算法由于指派问题的特殊性,又存在着由匈牙利数学家D.Konig 提出的更为简便的解法—匈牙利算法。
算法主要依据以下事实:如果系数矩阵)(ij c C =一行(或一列)中每一元素都加上或减去同一个数,得到一个新矩阵)(ij b B = ,则以C 或B 为系数矩阵的指派问题具有相同的最优指派。
利用上述性质,可将原系数阵C 变换为含零元素较多的新系数阵B ,而最优解不变。
若能在B 中找出n 个位于不同行不同列的零元素,令解矩阵中相应位置的元素取值为1,其它元素取值为零,则所得该解是以B 为系数阵的指派问题的最优解,从而也是原问题的最优解。
由C 到B 的转换可通过先让矩阵C 的每行元素均减去其所在行的最小元素得矩阵D ,D 的每列元素再减去其所在列的最小元素得以实现。
下面通过一例子来说明该算法。
例7 求解指派问题,其系数矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=16221917171822241819211722191516C 解 将第一行元素减去此行中的最小元素15,同样,第二行元素减去17,第三行元素减去17,最后一行的元素减去16,得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=06310157124074011B 再将第3列元素各减去1,得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=****20531005711407301B 以2B 为系数矩阵的指派问题有最优指派⎪⎪⎭⎫ ⎝⎛43124321 由等价性,它也是例7的最优指派。
有时问题会稍复杂一些。
例8 求解系数矩阵C 的指派问题⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=61071041066141512141217766698979712C 解:先作等价变换如下∨∨∨⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡→⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡----- 2636040*08957510*00*0032202*056107104106614151214121776669897971246767 容易看出,从变换后的矩阵中只能选出四个位于不同行不同列的零元素,但5=n ,最优指派还无法看出。

⼆分图匹配--匈⽛利算法⼆分图匹配--匈⽛利算法⼆分图匹配匈⽛利算法基本定义:⼆分图 —— 对于⽆向图G=(V,E),如果存在⼀个划分使V中的顶点分为两个互不相交的⼦集,且每个⼦集中任意两点间不存在边 ϵ∈E,则称图G为⼀个⼆分图。
⼆分图的充要条件是,G⾄少有两个顶点,且所有回路长度为偶数。
匹配 —— 边的集合,其中任意两条边都不存在公共顶点。
匹配边即是匹配中的元素,匹配点是匹配边的顶点,同样⾮匹配边,⾮匹配点相反定义。
最⼤匹配——在图的所有匹配中,包含最多边的匹配成为最⼤匹配 完美匹配——如果在⼀个匹配中所有的点都是匹配点,那么该匹配称为完美匹配。
附注:所有的完美匹配都是最⼤匹配,最⼤匹配不⼀定是完美匹配。
假设完美匹配不是最⼤匹配,那么最⼤匹配⼀定存在不属于完美匹配中的边,⽽图的所有顶点都在完美匹配中,不可能找到更多的边,所以假设不成⽴,及完美匹配⼀定是最⼤匹配。
交替路——从⼀个未匹配点出发,依次经过⾮匹配边,匹配边,⾮匹配边…形成的路径称为交替路,交替路不会形成环。
增⼴路——起点和终点都是未匹配点的交替路。
因为交替路是⾮匹配边、匹配边交替出现的,⽽增⼴路两端节点都是⾮匹配点,所以增⼴路⼀定有奇数条边。
⽽且增⼴路中的节点(除去两端节点)都是匹配点,所属的匹配边都在增⼴路径上,没有其他相连的匹配边,因此如果把增⼴路径中的匹配边和⾮匹配边的“⾝份”交换,就可以获得⼀个更⼤的匹配(该过程称为改进匹配)。
⽰例图Fig1_09_09.JPG注释:Fig3是⼀个⼆分图G=(V,E),V={1,2,3,4,5,6,7,8},E={(1,7),(1,5),(2,6),(3,5),(3,8),(4,5),(4,6)},该图可以重绘成Fig4,V可分成两个⼦集V={V1,V2},V1={1,2,3,4},V2={5,6,7,8}。
Fig4中的红⾊边集合就是⼀个匹配{(1,5),(4,6),(3,8)}Fig2中是最⼤匹配Fig1中红⾊边集合是完美匹配Fig1中交替路举例(4-6-2-7-1-5)Fig4中增⼴路(2-6-4-5-1-7)匈⽛利树匈⽛利树中从根节点到叶节点的路径均是交替路,且匈⽛利树的叶节点都是匹配点。



运筹学课程设计指派问题的匈牙利法专业:姓名:学号:1.算法思想:匈牙利算法的基本思想是修改效益矩阵的行或列,使得每一行或列中至少有一个为零的元素,经过修正后,直至在不同行、不同列中至少有一个零元素,从而得到与这些零元素相对应的一个完全分配方案。
当它用于效益矩阵时,这个完全分配方案就是一个最优分配,它使总的效益为最小。
这种方法总是在有限步內收敛于一个最优解。
该方法的理论基础是:在效益矩阵的任何行或列中,加上或减去一个常数后不会改变最优分配。
2.算法流程或步骤:1.将原始效益矩阵C的每行、每列各元素都依次减去该行、该列的最小元素,使每行、每列都至少出现一个0元素,以构成等价的效益矩阵C’。
2.圈0元素。
在C’中未被直线通过的含0元素最少的行(或列)中圈出一个0元素,通过这个0元素作一条竖(或横)线。
重复此步,若这样能圈出不同行不同列的n个0元素,转第四步,否则转第三步。
3.调整效益矩阵。
在C’中未被直线穿过的数集D中,找出最小的数d,D中所有数都减去d,C’中两条直线相交处的数都加的d。
去掉直线,组成新的等价效益矩阵仍叫C’,返回第二步。
X=0,这就是一种最优分配。
最低总4.令被圈0元素对应位置的X ij=1,其余ij耗费是C中使X=1的各位置上各元素的和。
ij算法流程图:3.算法源程序:#include<iostream.h>typedef struct matrix{float cost[101][101];int zeroelem[101][101];float costforout[101][101];int matrixsize;int personnumber;int jobnumber;}matrix;matrix sb;int result[501][2];void twozero(matrix &sb);void judge(matrix &sb,int result[501][2]);void refresh(matrix &sb);void circlezero(matrix &sb);matrix input();void output(int result[501][2],matrix sb);void zeroout(matrix &sb);matrix input(){matrix sb;int m;int pnumber,jnumber;int i,j;float k;char w;cout<<"指派问题的匈牙利解法:"<<endl;cout<<"求最大值,请输入1;求最小值,请输入0:"<<endl;cin>>m;while(m!=1&&m!=0){cout<<"请输入1或0:"<<endl;cin>>m;}cout<<"请输入人数(人数介于1和100之间):"<<endl;cin>>pnumber;while(pnumber<1||pnumber>100){cout<<"请输入合法数据:"<<endl;cin>>pnumber;}cout<<"请输入工作数(介于1和100之间):"<<endl;cin>>jnumber;while(jnumber<1||jnumber>100){cout<<"请输入合法数据:"<<endl;cin>>jnumber;}cout<<"请输入"<<pnumber<<"行"<<jnumber<<"列的矩阵,同一行内以空格间隔,不同行间以回车分隔,以$结束输入:\n";for(i=1;i<=pnumber;i++)for(j=1;j<=jnumber;j++){cin>>sb.cost[i][j];sb.costforout[i][j]=sb.cost[i][j];}cin>>w;if(jnumber>pnumber)for(i=pnumber+1;i<=jnumber;i++)for(j=1;j<=jnumber;j++){sb.cost[i][j]=0;sb.costforout[i][j]=0;}else{if(pnumber>jnumber)for(i=1;i<=pnumber;i++)for(j=jnumber+1;j<=pnumber;j++){sb.cost[i][j]=0;sb.costforout[i][j]=0;}}sb.matrixsize=pnumber;if(pnumber<jnumber)sb.matrixsize=jnumber;sb.personnumber=pnumber;sb.jobnumber=jnumber;if(m==1){k=0;for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)if(sb.cost[i][j]>k)k=sb.cost[i][j];for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)sb.cost[i][j]=k-sb.cost[i][j];}return sb;}void circlezero(matrix &sb){int i,j;float k;int p;for(i=0;i<=sb.matrixsize;i++)sb.cost[i][0]=0;for(j=1;j<=sb.matrixsize;j++)sb.cost[0][j]=0;for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)if(sb.cost[i][j]==0){sb.cost[i][0]++;sb.cost[0][j]++;sb.cost[0][0]++;}for(i=0;i<=sb.matrixsize;i++)for(j=0;j<=sb.matrixsize;j++)sb.zeroelem[i][j]=0;k=sb.cost[0][0]+1;while(sb.cost[0][0]<k){k=sb.cost[0][0];for(i=1;i<=sb.matrixsize;i++){if(sb.cost[i][0]==1){for(j=1;j<=sb.matrixsize;j++)if(sb.cost[i][j]==0&&sb.zeroelem[i][j]==0)break;sb.zeroelem[i][j]=1;sb.cost[i][0]--;sb.cost[0][j]--;sb.cost[0][0]--;if(sb.cost[0][j]>0)for(p=1;p<=sb.matrixsize;p++)if(sb.cost[p][j]==0&&sb.zeroelem[p][j]==0){sb.zeroelem[p][j]=2;sb.cost[p][0]--;sb.cost[0][j]--;sb.cost[0][0]--;}}}for(j=1;j<=sb.matrixsize;j++){if(sb.cost[0][j]==1){for(i=1;i<=sb.matrixsize;i++)if(sb.cost[i][j]==0&&sb.zeroelem[i][j]==0)break;sb.zeroelem[i][j]=1;sb.cost[i][0]--;sb.cost[0][j]--;sb.cost[0][0]--;if(sb.cost[i][0]>0)for(p=1;p<=sb.matrixsize;p++)if(sb.cost[i][p]==0&&sb.zeroelem[i][p]==0){sb.zeroelem[i][p]=2;sb.cost[i][0]--;sb.cost[0][p]--;sb.cost[0][0]--;}}}}if(sb.cost[0][0]>0)twozero(sb);elsejudge(sb,result);}void twozero(matrix &sb){int i,j;int p,q;int m,n;float k;matrix st;for(i=1;i<=sb.matrixsize;i++)if(sb.cost[i][0]>0)break;if(i<=sb.matrixsize){for(j=1;j<=sb.matrixsize;j++){st=sb;if(sb.cost[i][j]==0&&sb.zeroelem[i][j]==0){sb.zeroelem[i][j]=1;sb.cost[i][0]--;sb.cost[0][j]--;sb.cost[0][0]--;for(q=1;q<=sb.matrixsize;q++)if(sb.cost[i][q]==0&&sb.zeroelem[i][q]==0){sb.zeroelem[i][q]=2;sb.cost[i][0]--;sb.cost[0][q]--;sb.cost[0][0]--;}for(p=1;p<=sb.matrixsize;p++)if(sb.cost[p][j]==0&&sb.zeroelem[p][j]==0){sb.zeroelem[p][j]=2;sb.cost[p][0]--;sb.cost[0][j]--;sb.cost[0][0]--;}k=sb.cost[0][0]+1;while(sb.cost[0][0]<k){k=sb.cost[0][0];for(p=i+1;p<=sb.matrixsize;p++){if(sb.cost[p][0]==1){for(q=1;q<=sb.matrixsize;q++)if(sb.cost[p][q]==0&&sb.zeroelem[p][q]==0)break;sb.zeroelem[p][q]=1;sb.cost[p][0]--;sb.cost[0][q]--;sb.cost[0][0]--;for(m=1;m<=sb.matrixsize;m++)if(sb.cost[m][q]=0&&sb.zeroelem[m][q]==0){sb.zeroelem[m][q]=2;sb.cost[m][0]--;sb.cost[0][q]--;sb.cost[0][0]--;}}}for(q=1;q<=sb.matrixsize;q++){if(sb.cost[0][q]==1){for(p=1;p<=sb.matrixsize;p++)if(sb.cost[p][q]==0&&sb.zeroelem[p][q]==0)break;sb.zeroelem[p][q]=1;sb.cost[p][q]--;sb.cost[0][q]--;sb.cost[0][0]--;for(n=1;n<=sb.matrixsize;n++)if(sb.cost[p][n]==0&&sb.zeroelem[p][n]==0){sb.zeroelem[p][n]=2;sb.cost[p][0]--;sb.cost[0][n]--;sb.cost[0][0]--;}}}}if(sb.cost[0][0]>0)twozero(sb);elsejudge(sb,result);}sb=st;}}}void judge(matrix &sb,int result[501][2]){int i,j;int m;int n;int k;m=0;for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==1)m++;if(m==sb.matrixsize){k=1;for(n=1;n<=result[0][0];n++){for(i=1;i<=sb.matrixsize;i++){for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==1)break;if(i<=sb.personnumber&&j<=sb.jobnumber)if(j!=result[k][1])break;k++;}if(i==sb.matrixsize+1)break;elsek=n*sb.matrixsize+1;}if(n>result[0][0]){k=result[0][0]*sb.matrixsize+1;for(i=1;i<=sb.matrixsize;i++)for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==1){result[k][0]=i;result[k++][1]=j;}result[0][0]++;}}else{refresh(sb);}}void refresh(matrix &sb){int i,j;float k;int p;k=0;for(i=1;i<=sb.matrixsize;i++){for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==1){sb.zeroelem[i][0]=1;break;}}while(k==0){k=1;for(i=1;i<=sb.matrixsize;i++)if(sb.zeroelem[i][0]==0){sb.zeroelem[i][0]=2;for(j=1;j<=sb.matrixsize;j++)if(sb.zeroelem[i][j]==2){sb.zeroelem[0][j]=1;}}for(j=1;j<=sb.matrixsize;j++){if(sb.zeroelem[0][j]==1){sb.zeroelem[0][j]=2;for(i=1;i<=sb.matrixsize;i++)if(sb.zeroelem[i][j]==1){sb.zeroelem[i][0]=0;k=0;}}}}p=0;k=0;for(i=1;i<=sb.matrixsize;i++){if(sb.zeroelem[i][0]==2){for(j=1;j<=sb.matrixsize;j++){if(sb.zeroelem[0][j]!=2)if(p==0){k=sb.cost[i][j];p=1;}else{if(sb.cost[i][j]<k)k=sb.cost[i][j];}}}}for(i=1;i<=sb.matrixsize;i++){if(sb.zeroelem[i][0]==2)for(j=1;j<=sb.matrixsize;j++)sb.cost[i][j]=sb.cost[i][j]-k;}for(j=1;j<=sb.matrixsize;j++){if(sb.zeroelem[0][j]==2)for(i=1;i<=sb.matrixsize;i++)sb.cost[i][j]=sb.cost[i][j]+k;}for(i=0;i<=sb.matrixsize;i++)for(j=0;j<=sb.matrixsize;j++)sb.zeroelem[i][j]=0;circlezero(sb);}void zeroout(matrix &sb){int i,j;float k;for(i=1;i<=sb.matrixsize;i++){k=sb.cost[i][1];for(j=2;j<=sb.matrixsize;j++)if(sb.cost[i][j]<k)k=sb.cost[i][j];for(j=1;j<=sb.matrixsize;j++)sb.cost[i][j]=sb.cost[i][j]-k;}for(j=1;j<=sb.matrixsize;j++){k=sb.cost[1][j];for(i=2;i<=sb.matrixsize;i++)if(sb.cost[i][j]<k)k=sb.cost[i][j];for(i=1;i<=sb.matrixsize;i++)sb.cost[i][j]=sb.cost[i][j]-k;}}void output(int result[501][2],matrix sb) {int k;int i;int j;int p;char w;float v;v=0;for(i=1;i<=sb.matrixsize;i++){v=v+sb.costforout[i][result[i][1]];}cout<<"最优解的目标函数值为"<<v;k=result[0][0];if(k>5){cout<<"解的个数超过了限制."<<endl;k=5;}for(i=1;i<=k;i++){cout<<"输入任意字符后输出第"<<i<<"种解."<<endl;cin>>w;p=(i-1)*sb.matrixsize+1;for(j=p;j<p+sb.matrixsize;j++)if(result[j][0]<=sb.personnumber&&result[j][1]<=sb.jobnumber)cout<<"第"<<result[j][0]<<"个人做第"<<result[j][1]<<"件工作."<<endl;}}void main(){result[0][0]=0;sb=input();zeroout(sb);circlezero(sb);output(result,sb);}4. 算例和结果:自己运算结果为:->⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡3302102512010321->⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡330110241200032034526635546967562543----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡可以看出:第1人做第4件工作;第2人做第1件工作;第3人做第3件工作;第4人做第2件工作。
超详细匈⽛利算法流程以及Python程序实现通俗易懂前不久在⽆⼈机检测跟踪的项⽬中⽤到了多⽬标跟踪算法(该项⽬后续会发贴介绍),其中需要涉及多个⽬标在两帧之间的匹配问题,最初使⽤的是最简单的距离最⼩化原则进⾏帧间多⽬标的匹配。
后来通过实习和查阅论⽂等渠道了解到了多⽬标跟踪领域经典的Sort和DeepSort算法,其中都使⽤到了匈⽛利算法解决匹配问题,因此开此贴记录⼀下算法的学习过程。
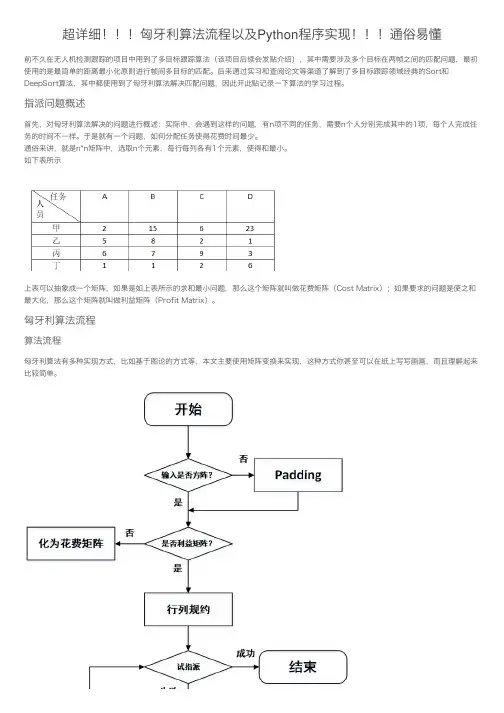
指派问题概述⾸先,对匈⽛利算法解决的问题进⾏概述:实际中,会遇到这样的问题,有n项不同的任务,需要n个⼈分别完成其中的1项,每个⼈完成任务的时间不⼀样。
于是就有⼀个问题,如何分配任务使得花费时间最少。
通俗来讲,就是n*n矩阵中,选取n个元素,每⾏每列各有1个元素,使得和最⼩。
如下表所⽰上表可以抽象成⼀个矩阵,如果是如上表所⽰的求和最⼩问题,那么这个矩阵就叫做花费矩阵(Cost Matrix);如果要求的问题是使之和最⼤化,那么这个矩阵就叫做利益矩阵(Profit Matrix)。
匈⽛利算法流程算法流程匈⽛利算法有多种实现⽅式,⽐如基于图论的⽅式等,本⽂主要使⽤矩阵变换来实现,这种⽅式你甚⾄可以在纸上写写画画,⽽且理解起来⽐较简单。
本⽂算法流程如上图所⽰,⾸先进⾏列规约,即每⾏减去此⾏最⼩元素,每⼀列减去该列最⼩元素,规约后每⾏每列中必有0元素出现。
接下来进⾏试指派,也就是划最少的线覆盖矩阵中全部的0元素,如果试指派的独⽴0元素数等于⽅阵维度则算法结束,如果不等于则需要对矩阵进⾏调整,重复试指派和调整步骤直到满⾜算法结束条件。
以上是我简要描述的算法流程,值得⼀提的是,⽤矩阵变换求解的匈⽛利算法也有多种实现,主要不同就在于试指派和调整矩阵这块,但万变不离其宗都是为了⽤最少的线覆盖矩阵中全部的零元素。
咱们废话少说,来看⼀个例⼦。
程序实现完整代码(带测试⽤例)'''@Date: 2020/2/23@Author:ZhuJunHui@Brief: Hungarian Algorithm using Python and NumPy'''import numpy as npimport collectionsimport timeclass Hungarian():""""""def__init__(self, input_matrix=None, is_profit_matrix=False):"""输⼊为⼀个⼆维嵌套列表is_profit_matrix=False代表输⼊是消费矩阵(需要使消费最⼩化),反之则为利益矩阵(需要使利益最⼤化) """if input_matrix is not None:# 保存输⼊my_matrix = np.array(input_matrix)self._input_matrix = np.array(input_matrix)self._maxColumn = my_matrix.shape[1]self._maxRow = my_matrix.shape[0]# 本算法必须作⽤于⽅阵,如果不为⽅阵则填充0变为⽅阵matrix_size =max(self._maxColumn, self._maxRow)pad_columns = matrix_size - self._maxRowpad_rows = matrix_size - self._maxColumnmy_matrix = np.pad(my_matrix,((0,pad_columns),(0,pad_rows)),'constant', constant_values=(0)) # 如果需要,则转化为消费矩阵if is_profit_matrix:my_matrix = self.make_cost_matrix(my_matrix)self._cost_matrix = my_matrixself._size =len(my_matrix)self._shape = my_matrix.shape# 存放算法结果self._results =[]self._totalPotential =0else:self._cost_matrix =Nonedef make_cost_matrix(self,profit_matrix):'''利益矩阵转化为消费矩阵,输出为numpy矩阵'''# 消费矩阵 = 利益矩阵最⼤值组成的矩阵 - 利益矩阵matrix_shape = profit_matrix.shapeoffset_matrix = np.ones(matrix_shape, dtype=int)* profit_matrix.max()cost_matrix = offset_matrix - profit_matrixreturn cost_matrixdef get_results(self):"""获取算法结果"""return self._resultsdef calculate(self):"""实施匈⽛利算法的函数"""result_matrix = self._cost_matrix.copy()# 步骤 1: 矩阵每⼀⾏减去本⾏的最⼩值for index, row in enumerate(result_matrix):result_matrix[index]-= row.min()# 步骤 2: 矩阵每⼀列减去本⾏的最⼩值for index, column in enumerate(result_matrix.T):result_matrix[:, index]-= column.min()#print('步骤2结果 ',result_matrix)#print('步骤2结果 ',result_matrix)# 步骤 3:使⽤最少数量的划线覆盖矩阵中所有的0元素# 如果划线总数不等于矩阵的维度需要进⾏矩阵调整并重复循环此步骤total_covered =0while total_covered < self._size:time.sleep(1)#print("---------------------------------------")#print('total_covered: ',total_covered)#print('result_matrix:',result_matrix)# 使⽤最少数量的划线覆盖矩阵中所有的0元素同时记录划线数量cover_zeros = CoverZeros(result_matrix)single_zero_pos_list = cover_zeros.calculate()covered_rows = cover_zeros.get_covered_rows()covered_columns = cover_zeros.get_covered_columns()total_covered =len(covered_rows)+len(covered_columns)# 如果划线总数不等于矩阵的维度需要进⾏矩阵调整(需要使⽤未覆盖处的最⼩元素)if total_covered < self._size:result_matrix = self._adjust_matrix_by_min_uncovered_num(result_matrix, covered_rows, covered_columns) #元组形式结果对存放到列表self._results = single_zero_pos_list# 计算总期望结果value =0for row, column in single_zero_pos_list:value += self._input_matrix[row, column]self._totalPotential = valuedef get_total_potential(self):return self._totalPotentialdef_adjust_matrix_by_min_uncovered_num(self, result_matrix, covered_rows, covered_columns):"""计算未被覆盖元素中的最⼩值(m),未被覆盖元素减去最⼩值m,⾏列划线交叉处加上最⼩值m"""adjusted_matrix = result_matrix# 计算未被覆盖元素中的最⼩值(m)elements =[]for row_index, row in enumerate(result_matrix):if row_index not in covered_rows:for index, element in enumerate(row):if index not in covered_columns:elements.append(element)min_uncovered_num =min(elements)#print('min_uncovered_num:',min_uncovered_num)#未被覆盖元素减去最⼩值mfor row_index, row in enumerate(result_matrix):if row_index not in covered_rows:for index, element in enumerate(row):if index not in covered_columns:adjusted_matrix[row_index,index]-= min_uncovered_num#print('未被覆盖元素减去最⼩值m',adjusted_matrix)#⾏列划线交叉处加上最⼩值mfor row_ in covered_rows:for col_ in covered_columns:#print((row_,col_))adjusted_matrix[row_,col_]+= min_uncovered_num#print('⾏列划线交叉处加上最⼩值m',adjusted_matrix)return adjusted_matrixclass CoverZeros():"""使⽤最少数量的划线覆盖矩阵中的所有零输⼊为numpy⽅阵""""""def__init__(self, matrix):# 找到矩阵中零的位置(输出为同维度⼆值矩阵,0位置为true,⾮0位置为false)self._zero_locations =(matrix ==0)self._zero_locations_copy = self._zero_locations.copy()self._shape = matrix.shape# 存储划线盖住的⾏和列self._covered_rows =[]self._covered_columns =[]def get_covered_rows(self):"""返回覆盖⾏索引列表"""return self._covered_rowsdef get_covered_columns(self):"""返回覆盖列索引列表"""return self._covered_columnsdef row_scan(self,marked_zeros):'''扫描矩阵每⼀⾏,找到含0元素最少的⾏,对任意0元素标记(独⽴零元素),划去标记0元素(独⽴零元素)所在⾏和列存在的0元素''' min_row_zero_nums =[9999999,-1]for index, row in enumerate(self._zero_locations_copy):#index为⾏号row_zero_nums = collections.Counter(row)[True]if row_zero_nums < min_row_zero_nums[0]and row_zero_nums!=0:#找最少0元素的⾏min_row_zero_nums =[row_zero_nums,index]#最少0元素的⾏row_min = self._zero_locations_copy[min_row_zero_nums[1],:]#找到此⾏中任意⼀个0元素的索引位置即可row_indices,= np.where(row_min)#标记该0元素#print('row_min',row_min)marked_zeros.append((min_row_zero_nums[1],row_indices[0]))#划去该0元素所在⾏和列存在的0元素#因为被覆盖,所以把⼆值矩阵_zero_locations中相应的⾏列全部置为falseself._zero_locations_copy[:,row_indices[0]]= np.array([False for _ in range(self._shape[0])])self._zero_locations_copy[min_row_zero_nums[1],:]= np.array([False for _ in range(self._shape[0])])def calculate(self):'''进⾏计算'''#储存勾选的⾏和列ticked_row =[]ticked_col =[]marked_zeros =[]#1、试指派并标记独⽴零元素while True:#print('_zero_locations_copy',self._zero_locations_copy)#循环直到所有零元素被处理(_zero_locations中没有true)if True not in self._zero_locations_copy:breakself.row_scan(marked_zeros)#2、⽆被标记0(独⽴零元素)的⾏打勾independent_zero_row_list =[pos[0]for pos in marked_zeros]ticked_row =list(set(range(self._shape[0]))-set(independent_zero_row_list))#重复3,4直到不能再打勾TICK_FLAG =Truewhile TICK_FLAG:#print('ticked_row:',ticked_row,' ticked_col:',ticked_col)TICK_FLAG =False#3、对打勾的⾏中所含0元素的列打勾for row in ticked_row:#找到此⾏row_array = self._zero_locations[row,:]#找到此⾏中0元素的索引位置#找到此⾏中0元素的索引位置for i in range(len(row_array)):if row_array[i]==True and i not in ticked_col:ticked_col.append(i)TICK_FLAG =True#4、对打勾的列中所含独⽴0元素的⾏打勾for row,col in marked_zeros:if col in ticked_col and row not in ticked_row:ticked_row.append(row)FLAG =True#对打勾的列和没有打勾的⾏画画线self._covered_rows =list(set(range(self._shape[0]))-set(ticked_row)) self._covered_columns = ticked_colreturn marked_zerosif __name__ =='__main__':#以下为3个测试⽤例cost_matrix =[[4,2,8],[4,3,7],[3,1,6]]hungarian = Hungarian(cost_matrix)print('calculating...')hungarian.calculate()print("Expected value:\t\t12")print("Calculated value:\t", hungarian.get_total_potential())# = 12print("Expected results:\n\t[(0, 1), (1, 0), (2, 2)]")print("Results:\n\t", hungarian.get_results())print("-"*80)profit_matrix =[[62,75,80,93,95,97],[75,80,82,85,71,97],[80,75,81,98,90,97],[78,82,84,80,50,98],[90,85,85,80,85,99],[65,75,80,75,68,96]]hungarian = Hungarian(profit_matrix, is_profit_matrix=True)hungarian.calculate()print("Expected value:\t\t543")print("Calculated value:\t", hungarian.get_total_potential())# = 543print("Expected results:\n\t[(0, 4), (2, 3), (5, 5), (4, 0), (1, 1), (3, 2)]")print("Results:\n\t", hungarian.get_results())print("-"*80)profit_matrix =[[62,75,80,93,0,97],[75,0,82,85,71,97],[80,75,81,0,90,97],[78,82,0,80,50,98],[0,85,85,80,85,99],[65,75,80,75,68,0]]hungarian = Hungarian(profit_matrix, is_profit_matrix=True)hungarian.calculate()print("Expected value:\t\t523")print("Calculated value:\t", hungarian.get_total_potential())# = 523print("Expected results:\n\t[(0, 3), (2, 4), (3, 0), (5, 2), (1, 5), (4, 1)]")print("Results:\n\t", hungarian.get_results())print("-"*80)print("-"*80)总结如开篇所⾔,匈⽛利算法具有多种实现⽅式,可见该算法多么优秀,本⽂的实现⽅式不⼀定是最优的,但相对⽽⾔⽐较通俗易懂。

匈牙利算法代码解析匈牙利算法又称作增广路算法,主要用于解决二分图最大匹配问题。
它的基本思想是在二分图中查找增广路,然后将这条增广路上的边反转,这样可以将匹配数增加一个,由此不断寻找增广路并反转边直到无法找到为止,最后所找到的就是二分图的最大匹配。
匈牙利算法的流程如下:1. 从左边开始选择一个未匹配的节点,将其标记为当前节点;2. 再从当前节点出发,依次寻找与它相连的未匹配节点;3. 如果找到了一个未匹配节点,则记录该节点的位置,并将当前节点标记为该节点;4. 如果当前节点的所有连边都不能找到未匹配节点,则退回到上一个节点,再往其他的连接点继续搜索;5. 如果到达已经匹配节点,则将该节点标记为新的当前节点,返回步骤4;6. 如果找到了一条增广路,则将其上的边反转,并将匹配数+1;7. 重复以上步骤,直至无法找到增广路为止。
在匈牙利算法中,增广路的查找可以使用DFS或BFS,这里我们以DFS为例进行解释。
匈牙利算法的时间复杂度为O(nm),n和m分别表示左边和右边的节点数,因为每条边至多遍历两次,所以最多需要执行2n次DFS。
以下为匈牙利算法的Python代码:```Pythondef findPath(graph, u, match, visited):for v in range(len(graph)):if graph[u][v] and not visited[v]:visited[v] = Trueif match[v] == -1 or findPath(graph, match[v], match, visited):# 如果v没有匹配或者匹配的右匹配节点能找到新的匹配match[v] = u # 更新匹配return Truereturn Falsedef maxMatching(graph):n = len(graph)match = [-1] * n # 右部节点的匹配数组,初始化为-1表示没有匹配count = 0return match, count```其中,findPath函数是用来查找增广路的DFS函数,match数组是右边节点的匹配数组,初始化为-1表示没有匹配,count则表示匹配数。

匈牙利算法描述匈牙利算法是图论中一种用于解决二分图匹配问题的算法。
它首次由匈牙利数学家Denzel匈牙利在1955年发表,因而得名。
匈牙利算法属于图匹配算法的范畴,在实际应用中有着很强的效率和准确性。
本文将介绍匈牙利算法的原理、实现方法和应用领域等相关内容。
一、匈牙利算法原理匈牙利算法是解决二分图最大匹配问题的经典算法之一。
在二分图中,匈牙利算法的目标是寻找图中的最大匹配,即尽可能多地找到满足匹配条件的边,也就是找到尽可能多的配对节点。
在匈牙利算法中,主要使用了增广路的概念,通过不断地寻找增广路,来不断地扩展匹配。
具体而言,匈牙利算法的核心思想是利用增广路径寻找最大匹配。
在每一次匹配的过程中,首先选择一个未匹配的节点,然后通过交替路径寻找增广路径,直到无法找到增广路径为止。
当无法找到增广路径时,说明找到了最大匹配。
增广路径指的是一条由未匹配的节点和匹配节点交替构成的路径,其中未匹配节点为起点和终点。
通过不断地寻找增广路径,可以逐步扩展匹配。
在匈牙利算法中,为了记录节点的匹配状态和寻找增广路径,通常使用匈牙利标号和匈牙利交错路的方式。
匈牙利标号是为每个节点标记一个代表节点匹配状态的值,而匈牙利交错路则是一种用于寻找增广路径的方法。
借助这些工具,匈牙利算法可以高效地解决最大匹配问题。
二、匈牙利算法实现方法匈牙利算法的实现方法较为复杂,需要结合图论和图匹配的相关知识。
在实际应用中,匈牙利算法通常通过编程实现,以解决特定的二分图匹配问题。
下面简要介绍匈牙利算法的一般实现方法。
1. 初始化匈牙利标号:首先对图中的所有未匹配节点进行初始化标号,即给它们赋予一个初始的匈牙利标号。
2. 寻找增广路径:选择一个未匹配的节点作为起点,通过交替路径和增广路的方法寻找增广路径。
在寻找增广路径的过程中,要根据节点的匈牙利标号来选择下一个节点,从而找到满足匹配条件的路径。
3. 匹配节点:如果成功找到一条增广路径,就可以将路径中的节点进行匹配,即将原来未匹配的节点与匹配节点进行匹配。
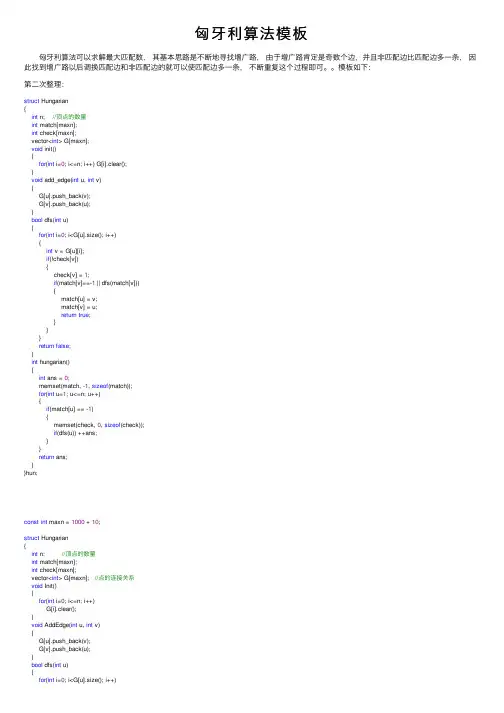
匈⽛利算法模板 匈⽛利算法可以求解最⼤匹配数,其基本思路是不断地寻找增⼴路,由于增⼴路肯定是奇数个边,并且⾮匹配边⽐匹配边多⼀条,因此找到增⼴路以后调换匹配边和⾮匹配边的就可以使匹配边多⼀条,不断重复这个过程即可。
模板如下:第⼆次整理:struct Hungarian{int n; //顶点的数量int match[maxn];int check[maxn];vector<int> G[maxn];void init(){for(int i=0; i<=n; i++) G[i].clear();}void add_edge(int u, int v){G[u].push_back(v);G[v].push_back(u);}bool dfs(int u){for(int i=0; i<G[u].size(); i++){int v = G[u][i];if(!check[v]){check[v] = 1;if(match[v]==-1 || dfs(match[v])){match[u] = v;match[v] = u;return true;}}}return false;}int hungarian(){int ans = 0;memset(match, -1, sizeof(match));for(int u=1; u<=n; u++){if(match[u] == -1){memset(check, 0, sizeof(check));if(dfs(u)) ++ans;}}return ans;}}hun;const int maxn = 1000 + 10;struct Hungarian{int n; //顶点的数量int match[maxn];int check[maxn];vector<int> G[maxn]; //点的连接关系void Init(){for(int i=0; i<=n; i++)G[i].clear();}void AddEdge(int u, int v){G[u].push_back(v);G[v].push_back(u);}bool dfs(int u){for(int i=0; i<G[u].size(); i++){int v = G[u][i];if(!check[v]) //不在增⼴路中{check[v] = 1;if(match[v]==-1 || dfs(match[v])) {match[u] = v;match[v] = u;return true;}}}return false; //不存在增⼴路}int hungarian(){int ans = 0;memset(match, -1, sizeof(match));for(int u=1; u<=n; u++){if(match[u] == -1){memset(check, 0, sizeof(check));if(dfs(u))++ans;}}return ans;}}hun;应⽤实例:USACO stall4/*ID: m1500293LANG: C++PROG: stall4*/#include <cstdio>#include <cstring>#include <algorithm>#include <vector>using namespace std;const int maxn = 1000 + 10;struct Hungarian{int n; //顶点的数量int match[maxn];int check[maxn];vector<int> G[maxn]; //点的连接关系void Init(){for(int i=0; i<=n; i++)G[i].clear();}void AddEdge(int u, int v){G[u].push_back(v);G[v].push_back(u);}bool dfs(int u){for(int i=0; i<G[u].size(); i++){int v = G[u][i];if(!check[v]) //不在增⼴路中{check[v] = 1;if(match[v]==-1 || dfs(match[v])) {match[u] = v;match[v] = u;return true;}}}return false; //不存在增⼴路}int hungarian(){int ans = 0;memset(match, -1, sizeof(match));for(int u=1; u<=n; u++){if(match[u] == -1){memset(check, 0, sizeof(check));if(dfs(u))++ans;}}return ans;}}hun;int main(){freopen("stall4.in", "r", stdin);freopen("stall4.out", "w", stdout);int N, M; //N个奶⽜ M个围栏scanf("%d%d", &N, &M);hun.n = N+M;hun.Init();for(int i=1; i<=N; i++){int num;scanf("%d", &num);while(num--){int t;scanf("%d", &t);hun.AddEdge(i, N+t);}}printf("%d\n", hun.hungarian());return0;}。
匈牙利算法数学模型
匈牙利算法是解决二分图最大匹配问题的一种算法,其数学模型如下:
假设有一个二分图G=(X, Y, E),其中X和Y分别表示左部顶点集和右部顶点集,E表示二者之间的边集。
对于一个匹配M而言,其由E中的边组成,使得M中的任何两条边都不共享任何顶点。
我们的目标是找到一个最大的匹配,使得匹配的边数最多。
具体实现过程中,可采用以下步骤:
1. 初始化一个最大匹配为空集M;
2. 对于每个左部顶点x,找到其能够匹配的右部顶点集合N(x);
3. 找到一个未被匹配的左部顶点x,在其能够匹配的右部顶点集合
N(x)中找到一个未被匹配的顶点y;
4. 如果y已经被匹配,将其所在的匹配边(u, y)加入到M中,同时将(x, y)加入到M中,使得u与x之间没有匹配边;
5. 如果y未被匹配,将(x, y)加入到M中,结束。
通过反复执行步骤三到五,直到所有的左部顶点都被匹配。
这样,M就是一个最大的匹配。
但是,匈牙利算法的时间复杂度较高,通常会采用优化方法来提高算法效率。