自动控制原理 典型系统分析
- 格式:doc
- 大小:516.00 KB
- 文档页数:12
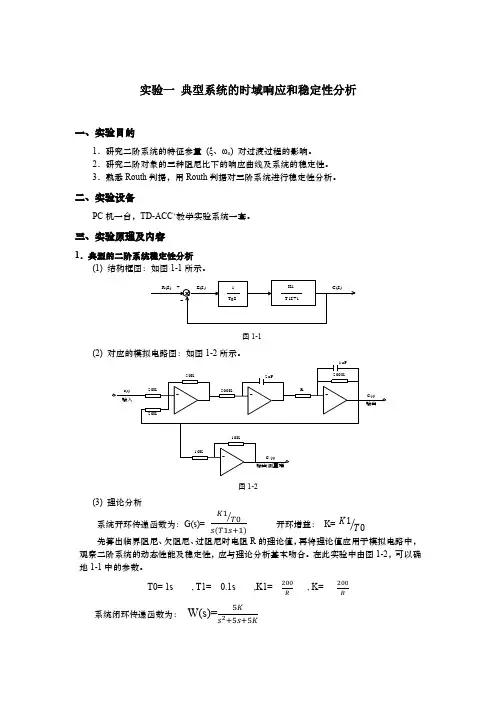
实验一典型系统的时域响应和稳定性分析一、实验目的1.研究二阶系统的特征参量(ξ、ωn) 对过渡过程的影响。
2.研究二阶对象的三种阻尼比下的响应曲线及系统的稳定性。
3.熟悉Routh判据,用Routh判据对三阶系统进行稳定性分析。
二、实验设备PC机一台,TD-ACC+教学实验系统一套。
三、实验原理及内容1.典型的二阶系统稳定性分析(1) 结构框图:如图1-1所示。
图1-1(2)图1-2(3) 理论分析系统开环传递函数为:G(s)=K1T0⁄s(T1s+1)开环增益:K= K1T0⁄先算出临界阻尼、欠阻尼、过阻尼时电阻R的理论值,再将理论值应用于模拟电路中,观察二阶系统的动态性能及稳定性,应与理论分析基本吻合。
在此实验中由图1-2,可以确地1-1中的参数。
T0= 1s , T1= 0.1s ,K1= 200R , K= 200R系统闭环传递函数为:W(s)=5Ks2+5s+5K其中自然振荡角频率:?n ω= 10√10R;阻尼比:?ζ= √10R402.典型的三阶系统稳定性分析(1) 结构框图:如图1-3所示。
图1-3(2) 模拟电路图:如图1-4所示。
图1-4(3) 理论分析系统的开环传函为: G(s)H(s)=20K s 3+12s 2+20s系统的特征方程为:1()()0G s H s += : s 3+12s 2+20s+20K=0 (4) 实验内容实验前由Routh 判断得Routh 行列式为:S 3 1 20 S 2 12 20K S 1 20-5/3*K 0 S 0 20K为了保证系统稳定,第一列各值应为正数,因此可以确定系统稳定 K 值的范围 : 0<K <12 R >41.7k系统临界稳定K: K=12 R =41.7k 系统不稳定K 值的范围: K >12 R <41.7k四、实验步骤1)将信号源单元的“ST ”端插针与“S ”端插针用“短路块”短接。

先进控制理论及其应用院系:班级:姓名:学号:前言20世纪70年代以来,随着计算机即使的广泛应用,自动控制技术有了很大的发展,先进过程控制(advanced process control,pac)应运而生。
先进过程控制也称先进控制。
它是具有比常规控制更好的控制效果的控制策略的系统,是提高过程控制质量、解决复杂赴欧成问题的理论和技术。
先进控制理论是建立在状态空间法基础上的一种控制理论,是自动控制理论的一个主要组成部分。
在先进控制理论中,对控制系统的分析和设计主要是通过对系统的状态变量的描述来进行的,基本的方法是时间域方法。
先进控制理论比经典控制理论所能处理的控制问题要广泛得多,包括线性系统和非线性系统,定常系统和时变系统,单变量系统和多变量系统。
先进控制理论的名称是在1960年以后开始出现的,用以区别当时已经相当成熟并在后来被称为经典控制理论的那些方法。
先进控制理论是在20世纪50年代中期迅速兴起的空间技术的推动下发展起来的。
空间技术的发展迫切要求建立新的控制原理,以解决诸如把宇宙火箭和人造卫星用最少燃料或最短时间准确地发射到预定轨道一类的控制问题。
这类控制问题十分复杂,采用经典控制理论难以解决。
1958年,苏联科学家Л.С.庞特里亚金提出了名为极大值原理的综合控制系统的新方法。
在这之前,美国学者R.贝尔曼于1954年创立了动态规划,并在1956年应用于控制过程。
他们的研究成果解决了空间技术中出现的复杂控制问题,并开拓了控制理论中最优控制理论这一新的领域。
1960~1961年,美国学者R.E.卡尔曼和R.S.布什建立了卡尔曼-布什滤波理论,因而有可能有效地考虑控制问题中所存在的随机噪声的影响,把控制理论的研究范围扩大,包括了更为复杂的控制问题。
几乎在同一时期内,贝尔曼、卡尔曼等人把状态空间法系统地引入控制理论中。
状态空间法对揭示和认识控制系统的许多重要特性具有关键的作用。
其中能控性和能观测性尤为重要,成为控制理论两个最基本的概念。

实验一、典型环节及其阶跃响应实验目的1、学习构成典型环节的模拟电路,了解电路参数对环节特性的影响。
2、学习典型环节阶跃响应的测量方法,并学会由阶跃响应曲线计算典型环节的传递函数。
实验内容构成下述典型环节的模拟电路,并测量其阶跃响应。
比例环节的模拟电路及其传递函数示图2-1。
G(S)=-R2/R1惯性环节的模拟电路及其传递函数示图2-2。
G(S)=-K/TS+1 K=R2/R1 ,T=R2*C积分环节的模拟电路及其传递函数示图2-3。
G(S)=1/TS T=RC微分环节的模拟电路及其传递函数示图2-4。
G(S)=-RCS比例加微分环节的模拟电路及其传递函数示图2-5。
G(S)=-K(TS+1) K=R2/R1 T=R2C比例加积分环节的模拟电路及其传递函数示图2-6。
G(S)=K(1+1/TS) K=R2/R1,T=R2C软件使用1、打开实验课题菜单,选中实验课题。
2、在课题参数窗口中,填写相应AD,DA或其它参数。
3、选确认键执行实验操作,选取消键重新设置参数。
实验步骤1、连接被测量典型环节的模拟电路及D/A、A/D连接,检查无误后接通电源。
2、启动应用程序,设置T和N。
参考值:T=0.05秒,N=200。
3、观测计算机屏幕示出的响应曲线及数据记录波形及数据(由实验报告确定)。
实验报告1、画出惯性环节、积分环节、比例加微分环节的模拟电路图,用坐标纸画出所有记录的惯性环节、积分环节、比例加微分环节的响应曲线。
2、由阶跃响应曲线计算出惯性环节、积分环节的传递函数,并与由电路计算的结果相比较。
实验二二阶系统阶跃响应一、实验目的1、研究二阶系统的特征参数,阻尼比ζ和无阻尼自然频ωn 对系统动态性能的影响,定量分析ζ和ωn与最大超调量Mp和调节时间 ts 之间的关系。
2、进一步学习实验仪器的使用方法。
3、学会根据系统阶跃响应曲线确定传递函数。
二、实验原理及电路典型二阶系统的闭环传递函数为其中ζ和ωn对系统的动态品质有决定的影响。



2014-2015学年第二学期自动控制原理实验报告姓名:王丽学号:20122527班级:交控3班指导教师:周慧实验一:典型系统的瞬态响应和稳定性1. 比例环节的阶跃响应曲线图(1:1)比例环节的阶跃响应曲线图(1:2)2. 积分环节的阶跃响应曲线图(c=1uf)3. 比例积分环节的阶跃响应曲线图(c=1uf)比例积分环节的阶跃响应曲线图(c=2uf)4. 惯性环节的阶跃响应曲线图(c=1uf)惯性环节的阶跃响应曲线图(c=2uf)5. 比例微分环节的阶跃响应曲线图(r=100k)比例微分环节的阶跃响应曲线图(r=200k)6. 比例积分微分环节的阶跃响应曲线图(r=100k)比例积分微分环节的阶跃响应曲线图(r=200k)实验结论1. 积分环节的阶跃响应曲线图可以看出,积分环节有两个明显的特征:(1)输出信号是斜坡信号(2)积分常数越大,达到顶峰需要的时间就越长2. 比例积分环节就是把比例环节与积分环节并联,分别取得结果之后再叠加起来,所以从图像上看,施加了阶跃信号以后,输出信号先有一个乘了系数K的阶跃,之后则逐渐按斜坡形式增加,形式同比例和积分的加和是相同的,因而验证了这一假设。
3. 微分环节对于阶跃信号的响应,在理论上,由于阶跃信号在施加的一瞬间有跳变,造成其微分结果为无穷大,之后阶跃信号不再变化,微分为0,表现为输出信号开始衰减。
4. PID环节同时具备了比例、积分、微分三个环节的特性,输出图像其实也就是三个环节输出特性的叠加。
三个环节在整个系统中的工作实际上是相互独立的,这也与它们是并联关系的事实相符合。
5.惯性环节的传递函数输出函数:可以看到,当t→∞时,r(t)≈Ku(t),这与图中的曲线是匹配的。
实验心得通过本实验我对试验箱更加熟悉,会连接电路;更直观的看到电路的数学模型和电路的响应曲线图三者之间的关系,这让我能够将在此之前所学的知识联系到一起。
不管是什么电路,如果要研究它首先就是得到它的数学模型,然后再通过对数学模型的研究间接的来研究该电路。

指导教师评定成绩:审定成绩:重庆邮电大学移通学院自动化系课程设计报告设计题目:Ⅰ型二阶系统的典型分析与综合设计学生姓名:专业:班级:学号:指导教师:设计时间:2010 年 12 月重庆邮电大学移通自动化系制重庆邮电大学移通学院《自动控制原理》课程设计(简明)任务书-供08级自动化专业、电气工程与自动化专业本科生用引言:《自动控制原理》课程设计是该课程的一个重要教学环节,它有别于毕业设计,更不同于课堂教学。
它主要是培养学生统筹运用自动控制原理课程中所学的理论知识,掌握反馈控制系统的基本理论和基本方法,对工程实际系统进行完整的全面的分析和综合。
一、设计题目:Ⅰ型二阶系统的典型分析与综合设计二、系统说明:该Ⅰ型系统物理模拟结构如下图:其中R0=100KΩ; C1=C2=10-5F;R2=1/2 R0R f为线性滑动电位器,可调范围为:10-1R0~ 104R0 ,设计过程中可忽略各种干扰,比如:运算放大器的零点漂移,环节间的负载效应,外界强力电力设备产生的电磁干扰等,均可忽略。
三、系统参量:系统输入信号:r(t);系统输出信号:y(t);四、设计指标:设定:输入为r(t)=a+bt(其中:a=5rad/secb=4rad/sec)在保证静态指标K v=5(e ss≤0.8)的前提下,要求动态期望指标:σp% ≤8.5% ;t s≤2sec五、基本要求:1. 建立系统数学模型——传递函数;2. 利用频率特性法分析和综合系统(学号为单号同学做);3. 利用根轨迹法分析和综合系统(学号位双号同学做);4. 完成系统综合前后的有源物理模拟(验证)实验;5. 完成系统综合前后的计算机仿真(验证)实验;六、设计缴验:1. 课程设计计算说明书一份;2. 原系统组成结构原理图一张(自绘);3. 系统分析,综合用BODE图(或根轨迹图)各一张;4. 系统综合前后的模拟图各一张(附实验结果图)各一张;5. 计算机仿真程序框图一张;6. 计算机仿真程序清单一份(附仿真实验结果图);7. 封面装帧成册;移通学院自动化系指导教师:汪纪峰2010-12-15目录引言 (2)一、系统概述 (7)1.1 设计目的 (7)1.2 系统的工作原理 (7)1.3 系统设计基本要求 (8)二、系统建模 (9)2.1 各环节建模 (9)2.1.1 比较器 (9)2.1.2 比例环节 (9)2.1.3 积分环节 (10)2.1.4 惯性环节 (11)2.1.5 反馈环节 (12)2.2 系统模型 (12)2.2.1 系统框图模型 (12)2.2.2 系统等价框图 (12)2.2.3 系统频域模型 (13)2.2.4 小结 (13)三、系统分析 (14)3.1 稳定性分析 (14)3.1.1 时域分析 (14)3.1.2 根轨迹映证 (14)3.1.2.1 绘制根轨迹 (15)3.2静态精度分析 (16)3.2.1Ⅰ型系统的典型分析 (16)3.2.1.1 跟踪能力 (16)3.2.1.2 ess计算 (16)3.2.2 根轨迹映证 (16)3.3 动态分析K 1 (17)3.3.1 作根轨迹 (18)3.3.2 指标分析 (19)四、系统综合 (20)4.1 校正方案的设计 (20)4.2 ts问题 (20)4.3τ的确定 (21)4.3.1 绘制校正后系统—τ参数根轨迹 (21)4.3.2 绘制τ参数根轨迹 (22)4.3.3 确定满足的σp%的ξ (24)4.3.4 做等ξ线 (24)4.4 确定τA (24)五、系统模拟 (25)5.1 原系统的物理模拟 (25)5.2校正后系统的物理模拟 (26)六、设计小结 (27)6.1心得体会 (27)6.2致谢 (28)七、参考文献 (29)《自动控制原理》课程设计第一章系统概述1.1设计目的主要是培养学生的统筹运用自动控制原理课程中所学的理论知识,掌握反馈控制系统的基本理论和方法,对工程实际系统进行完整全面分析和综合。

自动控制理论实验报告姓名罗晋学号201623010505班级电气F1606同组人实验一典型系统的阶跃响应分析一、实验目的1. 熟悉一阶系统、二阶系统的阶跃响应特性及模拟电路;2. 测量一阶系统、二阶系统的阶跃响应曲线,并了解参数变化对其动态特性的影响;3. 掌握系统动态性能的测试方法。
二、实验内容1. 设计并搭建一阶系统、二阶系统的模拟电路;2. 观测一阶系统的阶跃响应,并研究参数变化对其输出响应的影响;σ、3. 观测二阶系统的阻尼比0<ξ<1时的单位阶跃响应曲线;并求取系统的超调量%调节时间t s(Δ= ±0.05);并研究参数变化对其输出响应的影响。
三、实验结果(一)一阶系统阶跃响应研究1. 一阶系统模拟电路如图1-1所示,推导其传递函数G(s)=K/(Ts+1),其中R0=200K。
图1-1 一阶系统模拟电路2. 将阶跃信号发生器的输出端接至系统的输入端。
3. 若K=1、T=1s时,取:R1=100K,R2=100K,C=10uF(K= R2/ R1=1,T=R2C=100K×10uF=1)。
当T=1,光标为起点和终值:光标为起点和0.95的终值:传递函数为:(R2/R1)/(R2CS+1)4 若K=1、T=0.1s时,重复上述步骤(R1=100K,R2=100K,C=1uF(K= R2/ R1=1,T=R2C=100K×1uF=0.1))。
当T=0.1时,光标为起点和终值;光标为起点和0.95终值:6. 保存实验过程中的波形,记录相关的实验数据.,参数变化对系统动态特性的影响分析。
传递函数为:(R2/R1)/(R2CS+1), t=3T ,当T 减小需要达到稳定的时间也会减少,(二)二阶系统阶跃响应研究二阶系统模拟电路如图1-2所示,Rx 阻值可调范围为0~470K 。
图1-2 二阶系统模拟电路传递函数为1. n ω值一定(取10n ω=)时:1.1 当ξ=0.2时,各元件取值:C=1uF ,R=100K , R X =250K (实际操作时可用200k+51k=251k 代替),理论计算系统的%σ,t s (Δ= ±0.05),记录此时系统的阶跃响应曲线(阶跃信号的幅值自定),在曲线上求取系统的%σ,t s (Δ= ±0.05),并与理论值进行比较。
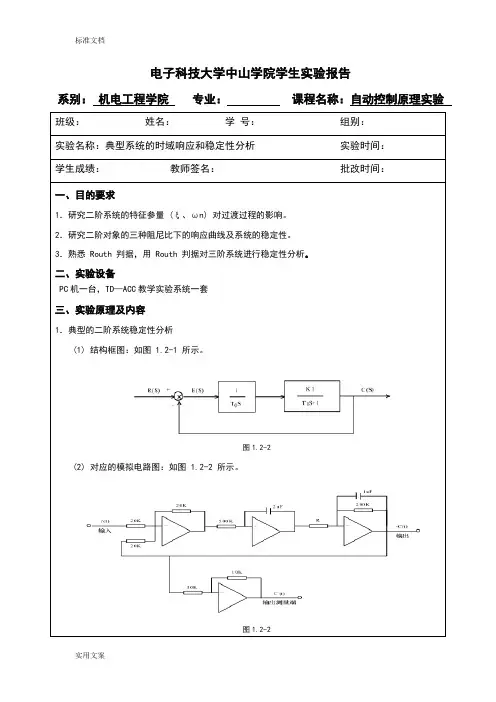
系别:机电工程学院专业:课程名称:自动控制原理实验班级:姓名:学号:组别:实验名称:典型系统的时域响应和稳定性分析实验时间:学生成绩:教师签名:批改时间:一、目的要求1.研究二阶系统的特征参量 (ξ、ωn) 对过渡过程的影响。
2.研究二阶对象的三种阻尼比下的响应曲线及系统的稳定性。
3.熟悉 Routh 判据,用 Routh 判据对三阶系统进行稳定性分析。
二、实验设备PC机一台,TD—ACC教学实验系统一套三、实验原理及内容1.典型的二阶系统稳定性分析(1) 结构框图:如图 1.2-1 所示。
图1.2-2(2) 对应的模拟电路图:如图 1.2-2 所示。
图1.2-2系别:机电工程学院专业:课程名称:自动控制原理实验班级:姓名:学号:组别:实验名称:实验时间:学生成绩:教师签名:批改时间:(3) 理论分析系统开环传递函数为:;开环增益:(4) 实验内容先算出临界阻尼、欠阻尼、过阻尼时电阻 R 的理论值,再将理论值应用于模拟电路中,观察二阶系统的动态性能及稳定性,应与理论分析基本吻合。
在此实验中(图 1.2-2),系统闭环传递函数为:其中自然振荡角频率:2.典型的三阶系统稳定性分析(1) 结构框图:如图 1.2-3 所示。
系别:机电工程学院专业:课程名称:自动控制原理实验班级:姓名:学号:组别:实验名称:实验时间:学生成绩:教师签名:批改时间:图 1.2-3(2)模拟电路图:如图 1.2-4 所示。
图 1.2-4(3)理论分析:系统的特征方程为:(4)实验内容:实验前由 Routh 判断得 Routh 行列式为:系别:机电工程学院专业:课程名称:自动控制原理实验班级:姓名:学号:组别:实验名称:实验时间:学生成绩:教师签名:批改时间:为了保证系统稳定,第一列各值应为正数,所以有五、实验步骤1.将信号源单元的“ST”端插针与“S”端插针用“短路块”短接。
由于每个运放单元均设臵了锁零场效应管,所以运放具有锁零功能。

自动控制原理(全套课件)一、引言自动控制原理是自动化领域的一门重要学科,它主要研究如何利用各种控制方法,使系统在受到扰动时,能够自动地、准确地、快速地恢复到平衡状态。
本课件将详细介绍自动控制的基本概念、控制系统的类型、数学模型、稳定性分析、控制器设计等内容,帮助学员全面掌握自动控制原理的基本理论和方法。
二、控制系统的基本概念1. 自动控制自动控制是指在没有人直接参与的情况下,利用控制器使被控对象按照预定规律运行的过程。
自动控制的核心在于控制器的设计,它能够根据被控对象的运行状态,自动地调整控制量,使系统达到预期的性能指标。
2. 控制系统控制系统是由被控对象、控制器、传感器和执行器等组成的闭环系统。
被控对象是指需要控制的物理过程或设备,控制器负责产生控制信号,传感器用于测量被控对象的运行状态,执行器则根据控制信号对被控对象进行操作。
三、控制系统的类型1. 按控制方式分类(1)开环控制系统:控制器不依赖于被控对象的运行状态,直接产生控制信号。
开环控制系统简单,但抗干扰能力较差。
(2)闭环控制系统:控制器依赖于被控对象的运行状态,通过反馈环节产生控制信号。
闭环控制系统抗干扰能力强,但设计复杂。
2. 按控制信号分类(1)连续控制系统:控制信号是连续变化的,如模拟控制系统。
(2)离散控制系统:控制信号是离散变化的,如数字控制系统。
四、控制系统的数学模型1. 微分方程模型微分方程模型是描述控制系统动态性能的一种数学模型,它反映了系统输入、输出之间的微分关系。
通过求解微分方程,可以得到系统在不同时刻的输出值。
2. 传递函数模型传递函数模型是描述控制系统稳态性能的一种数学模型,它反映了系统输入、输出之间的频率响应关系。
传递函数可以通过拉普拉斯变换得到,它是控制系统分析、设计的重要工具。
五、控制系统的稳定性分析1. 李雅普诺夫稳定性分析:通过构造李雅普诺夫函数,分析系统的稳定性。
2. 根轨迹分析:通过分析系统特征根的轨迹,判断系统的稳定性。
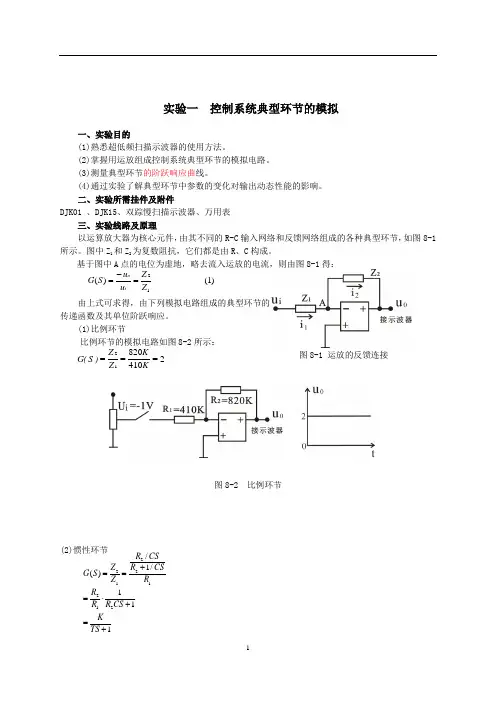
实验一 控制系统典型环节的模拟一、实验目的(1)熟悉超低频扫描示波器的使用方法。
(2)掌握用运放组成控制系统典型环节的模拟电路。
(3)测量典型环节的阶跃响应曲线。
(4)通过实验了解典型环节中参数的变化对输出动态性能的影响。
二、实验所需挂件及附件DJK01 、DJK15、双踪慢扫描示波器、万用表三、实验线路及原理以运算放大器为核心元件,由其不同的R-C 输入网络和反馈网络组成的各种典型环节,如图8-1所示。
图中Z 1和Z 2为复数阻抗,它们都是由R 、C 构成。
基于图中A 点的电位为虚地,略去流入运放的电流,则由图8-1得:由上式可求得,由下列模拟电路组成的典型环节的传递函数及其单位阶跃响应。
(1)比例环节比例环节的模拟电路如图8-2所示:图8-1 运放的反馈连接图8-2 比例环节(2)惯性环节 (1) )(12Z Z u u S G i o =-=2=410820==12K K Z Z )S (G 111/1/)(21212212+=+⋅=+==TS K CS R R R R CS R CS R Z Z S G取参考值R 1=100K ,R 2=100K ,C=1uF图8-3 惯性环节(3)积分环节式中积分时间常数T=RC,取参考值R=200K ,C=1uF图8-4 积分环节(4)比例微分环节(PD ),其接线图如图及阶跃响应如图8-5所示。
参考值R 1=200K ,R 2=410K ,C=0.1uF)(3 1 1 /1)(12TS RCS R CS Z Z S G ====C R =T , =K (4) 1+= 1+•= 1+==1D 1211211212R R )S T (K )CS R (R R CS /R CS /R R Z Z )S (G D其中图8-5 比例微分环节(5)比例积分环节,其接线图单位阶跃响应如图8-6所示。
参考值R 1=100K R 2=200K C=0.1uF图8-6 比例积分环节(6)振荡环节,其原理框图、接线图及单位阶跃响应波形分别如图8-7、8-8所示。
自动控制原理实验报告班级:自动化0906班学生: 伍振希(09213052)张小维(合作)任课教师:苗宇老师目录实验一典型环节及其阶跃响应 (1)一、实验目的 (1)二、实验仪器 (1)三、实验原理 (1)四、实验内容 (1)五、实验步骤 (2)六、实验结果 (3)实验二二阶系统阶跃响应 (6)一、实验目的 (6)二、实验仪器 (6)三、实验原理 (6)四、实验内容 (6)五、实验步骤 (7)六、实验结果 (7)实验三连续系统串联校正 (13)一、实验目的 (13)二、实验仪器 (13)三、实验内容 (13)四、实验步骤 (15)五、实验结果 (15)实验一典型环节及其阶跃响应一、实验目的1. 掌握控制模拟实验的基本原理和一般方法。
2. 掌握控制系统时域性能指标的测量方法。
二、实验仪器1.EL-AT-III型自动控制系统实验箱一台2.计算机一台三、实验原理1.模拟实验的基本原理:控制系统模拟实验采用复合网络法来模拟各种典型环节,即利用运算放大器不同的输入网络和反馈网络模拟各种典型环节,然后按照给定系统的结构图将这些模拟环节连接起来,便得到了相应的模拟系统。
再将输入信号加到模拟系统的输入端,并利用计算机等测量仪器,测量系统的输出,便可得到系统的动态响应曲线及性能指标。
若改变系统的参数,还可进一步分析研究参数对系统性能的影响。
四、实验内容构成下述典型一阶系统的模拟电路,并测量其阶跃响应:1.比例环节的模拟电路及其传递函数如图1-1。
G(S)= R2/R12.惯性环节的模拟电路及其传递函数如图1-2。
G(S)= - K/TS+1K=R2/R1,T=R2C3.积分环节的模拟电路及传递函数如图1-3。
G(S)=1/TST=RC4.微分环节的模拟电路及传递函数如图1-4。
G(S)= - RCS5.比例微分环节的模拟电路及传递函数如图1-5(未标明的C=0.01uf)。
G(S)= -K(TS+1)K=R2/R1,T=R1C五、实验步骤1.启动计算机,在桌面双击图标 [自动控制实验系统] 运行软件。
《自动控制原理》实验报告姓名:学号:专业:班级:时段:成绩:工学院自动化系实验一 典型环节的MATLAB 仿真一、实验目的1.熟悉MATLAB 桌面和命令窗口,初步了解SIMULINK 功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、实验原理1.比例环节的传递函数为K R K R R RZ ZsG 200,1002)(211212==-=-=-=其对应的模拟电路及SIMULINK 图形如图1-3所示。
三、实验内容按下列各典型环节的传递函数,建立相应的SIMULINK 仿真模型,观察并记录其单位阶跃响应波形。
① 比例环节1)(1=s G 和2)(1=s G ; ② 惯性环节11)(1+=s s G 和15.01)(2+=s s G ③ 积分环节s s G 1)(1= ④ 微分环节s s G =)(1图1-3 比例环节的模拟电路及SIMULINK 图形⑤ 比例+微分环节(PD )2)(1+=s s G 和1)(2+=s s G ⑥ 比例+积分环节(PI )s s G 11)(1+=和s s G 211)(2+=四、实验结果及分析① 仿真模型及波形图1)(1=s G 和2)(1=s G② 仿真模型及波形图11)(1+=s s G 和15.01)(2+=s s G 11)(1+=s s G 15.01)(2+=s s G③ 积分环节ss G 1)(1=④微分环节⑤比例+微分环节(PD)⑥比例+积分环节(PI)五、分析及心得体会实验二线性系统时域响应分析一、实验目的1.熟练掌握step( )函数和impulse( )函数的使用方法,研究线性系统在单位阶跃、单位脉冲及单位斜坡函数作用下的响应。
2.通过响应曲线观测特征参量ζ和ω对二阶系统性能的影响。
n3.熟练掌握系统的稳定性的判断方法。
二、基础知识及MATLAB函数(一)基础知识时域分析法直接在时间域中对系统进行分析,可以提供系统时间响应的全部信息,具有直观、准确的特点。
自动控制原理总经典总结自动控制原理》总复控制系统控制系统是由受控对象和控制器组成的系统,用于控制和调节被控量。
根据不同的角度,控制系统可以分为恒值系统和随动系统、线性系统和非线性系统、连续系统和离散系统、定常系统和时变系统等。
线性系统线性系统是指系统的输出与输入之间存在线性关系的系统。
建模时可以采用求传函或脉冲传函的方法,分析时可使用根轨迹法、频率特性法等方法。
非线性系统非线性系统是指系统的输出与输入之间不存在线性关系的系统。
建模时可以采用描述函数法或相平面法,稳定性分析时可以求奇点和极限环,运动时间可以通过振幅和频率计算得出。
控制系统的基本概念控制系统的基本术语包括自动控制、系统、自动控制系统、被控量、输入量、干扰量、受控对象、控制器、反馈、负反馈控制原理等。
掌握这些基本概念可以帮助理解控制系统的基本组成和工作原理。
基本控制方式控制系统的基本方式包括开环控制系统、闭环控制系统和复合控制系统。
开环控制系统没有反馈,闭环控制系统则通过反馈控制来实现对被控量的调节,复合控制系统则是开环控制和闭环控制的组合。
数学模型数学模型是用数学表达式描述控制系统的工作原理和特性的模型。
建模时可以采用物理系统的微分方程描述、拉普拉斯变换及反变换、传递函数及典型环节的传递函数、脉冲响应函数等方法。
图形表示可以采用结构图、信号流图等方法。
基本要求研究自动控制原理需要掌握控制系统的基本概念、基本控制方式、数学模型等知识。
同时,需要了解控制系统的分类和典型输入信号,并能够正确理解数学模型的特点和概念。
掌握这些知识可以帮助理解控制系统的工作原理和实际应用。
2.了解动态微分方程建立的一般方法和小偏差线性化方法。
3.掌握使用拉普拉斯变换解微分方程的方法,并对解的结构、运动模态、特征根的关系、零输入响应、零状态响应等概念有清晰的理解。
4.正确理解传递函数的定义、性质和意义,并熟练掌握系统开环传递函数、闭环传递函数、误差传递函数、典型环节传递函数等概念。
222010322072023 付珣利自动化01班位置随动系统:
控制系统原理图
(作业一)
1.1系统方块图
1.2控制方案
若电网电压受到波动,ui↑则δu↑u↑n↑uo↑
所以δu↓u↓n↓从而使n达到稳定。
(作业二)
2.1由原理可知:
Θe (s )=Θi (s )—Θ0(s ) US (s )=K0Θe (s )
Us (s )=Raia(s)+LaSia+Eb (s ) M(s)=C m ia(s) JS 2θ0(S)+fs θ
(S)= M(s)-Mc (s) Eb(s)=Kb θ0(S)
2.2系统传递函数
)
()(0s s i θθ=
()
)
)((1))((1)(1))((3
2103
210f JS R S L S K C f JS R S L S C K K K K f
JS R S L S K C f JS R S L S C K K K K a a b
m a a m
a a b
m a a m
+++
++++++
++=
m b m a a m
C K K K K K C f JS R S L S C K K K K 32103210))((++++
2.3动态结构图
设定参数:f=20N,J=20K ·m ²,a R =20 Ω,La=1H,Ko=40,k1k2k3=100,Cm=1,Kb=0 (因为暂取Kb=0,测速反馈通道相当于没加进)
图.动态结构图
则开环传递函数为:G(s)=
)
105.0)(1(10
++s s s
闭环传递函数:Ψ(s )=10
)105.0)(1(10
+++s s s
2.4信号流图
(作业三)系统性能
3.1系统响应及动态性能指标 单位阶跃响应曲线:
由阶跃响应曲线可得知:系统是稳定的,但震荡次数较多。
由闭环主导极点
的概念,S1>>S2可将系统近似处理为:开环传递函数G(s)=
)
1(10+s s ,此时的相
对阻尼系数ζ=0.5,δ=1.34%,Wn=1,调节时间ts=3.5/ξWn=7s ,tp=π /21ξ-n w =3.625,tr=(π-β)/Wd=2.417. 近似处理后响应曲线如下:
分析:系统仍然稳定,震荡次数相对减小。
3.2两种常用方法校正 ①加入测速反馈(0.347s+1) 单位阶跃响应:
此时ζ=0.707为工程上的最佳参数,Wn 不变,ts 明显减小,δ%也明显减小,但是在斜坡输入响应下稳态误差变大,因为开环放大倍数变大。
②前向通道加入比例微分(0.414s+1) 响应曲线
此时ζ=0.707为工程上的最佳参数,Wn 不变,ts 明显减小,tp 也减小,δ%明显减小,稳态误差不变。
③比较:有曲线特性分析得到,引入测速反馈或前向通道加比例微分都将使ζ增大,超调减小,动态性能变好,同时不影响Wn ,且在适当时候还可取到最佳工作参数。
但测速会影响开环放大倍数K,从而影响稳定误差,此时可以同时调大比例系数避免。
前向通道加比例微分同样可提高系统性能,但对噪声抑制力变弱,由于加入零点,超调量变大,峰值时间减少,且随零点接近原点而影响加剧。
(作业四)绘制根轨迹
①开环传递函数G(s)=)
1(10 s s
num=[10]; den=[1 1 0]; rlocus(num,den)
由根轨迹可知此系统很是稳定。
②引入测速反馈后: num=[10];
den=[1 4.47 10];
rlocus(num,den)
③引入比例微分
num=[4.14 10];
den=[1 1 0];
rlocus(num,den)
(作业五)频域系统性能分析
①绘制Bode图
i原系统
ii引入测速反馈
iii引入比例微分
分析:观察bode图,可以发现有测速反馈的比原系统相角裕度r提高,比例微分r没变很大,r越高,谐振峰值Mr越小。
低频段中,加测速反馈的bode与纵轴交点大概30dB,而其它的均是60dB,说明k值受到影响并变小,所以稳定误差会加大。
中频段原系统斜率为-40dB,校正后由图中可以观察到变为-20dB,稳定性提高。
②绘制奈氏曲线
i原系统
ii引入测速反馈
iii引入比例微分
分析:由奈氏曲线极其数据可以看出,首先由奈氏稳定判据知三个系统均稳定,不过原系统不如引入测速或比例微分的稳定性强,再观察得到,随着w的增大,加比例微分的A(w)明显要比测速的增大的快,及响应较快,这是由比例微分中有附加零点而引起的。
(作业六)系统校正(PID法)
创建模拟系统,用PID校正。
PID参数选择:根据简易工程整定法,取P:kp=0.57k,I:0.5Tk,D:0.13Tk
创建Matlab中的模拟系统:
Subsystem.in1out1如右图:
PID参数设定:
校正后阶跃响应曲线:
Bode图:
奈氏曲线:
分析:
1.比起原响应曲线,校正后超调量受到一定控制,震荡次数明显减小,调节时间ts明显减小,系统仍然是稳定的。
2.观察bode图,可以发现,在低频段,校正后的系统与纵轴交点大概120dB几乎是原来的2倍,因而开环倍数必定增大,稳态误差必然降低。
中频段,原来斜率为-40,现在为-20,明显稳定性提高。
截止频率Wc比原来提高了,增加了系统的快速性,如图中红色注释,相角裕度r也明显增大,稳定裕度增大,谐振峰
值Mr随之也会减小,稳定性能与动态性能提高。
3.奈氏曲线前后相比较,可以发现,校正后系统更加平稳,而不是像原系统一样,在某一w处,A(w)突然突增,稳定度也越来越高。
(作业七)线性离散系统分析
在matlab中的模拟仿真:
分析:1.系统加入采样器使得上升时间略有提前,超调量增大,稳定度降低。
2.零阶保持器是上升时间加长,同时,超调量和震荡次数增加。
(作业八)非线性的系统
Matlab中的状态模型:(加饱和限幅的非线性因素)。