原子结构氢原子光谱理解玻尔理论对氢原子光谱的解释共45页
- 格式:ppt
- 大小:4.01 MB
- 文档页数:111




氢原子的能级与光谱·爱因斯坦1905年提出光量子的概念后,不受名人重视,甚至到1913年德国最著名的四位物理学家(包括普朗克)还把爱因斯坦的光量子概念说成是“迷失了方向”。
可是,当时年仅28岁的玻尔,却创造性地把量子概念用到了当时人们持怀疑的卢瑟福原子结构模型,解释了近30年的光谱之谜。
§1 氢原子的能级与光谱一、玻尔的氢原子理论(一)玻尔的基本假设1.定态假设:原子只可能处于一系列不连续的能量状态E1, E2, E3,…。
处于这些状态的原子是稳定的,电子虽作加速运动,但不辐射电磁波。
2.频率条件:原子从某一定态跃迁至另一定态时,则发射(或吸收)光子,其频率满足玻尔在此把普朗克常数引入了原子领域。
(二)玻尔的氢原子理论 1.电子在原子核电场中的运动(1)基本情况:核不动;圆轨道;非相对论。
(2) 用经典力学规律计算电子绕核的运动·电子受力:·能量:得f f = - 14πε0 ( )Ze 2r 21 ε0 ( ) Ze2 r = m ( )υ2r1 2E = m υ2 - 1 4πε0 ( ) Ze2 r E = -Ze 28πε0r2.轨道角动量量子化条件玻尔假定:在所有圆轨道中,只有电子的角动量满足下式的轨道才是可能的。
玻尔引进了角动量的量子化。
3.轨道和速度 ·r n = n 2r 1 ,(玻尔半径) r 1= 0.529 Å· υn= υ1/n ,4πε0h 2 r 1 = ( me 2 )( ) 1 Z 4πε0hυ1 = Ze 2)可见, 随n↑⇒r n↑,υn↓4.能级---能量量子化将r n代入前面E式中,有n = 1,2,3,…)R:里德伯常数(见后)基态能量:E1= -13.6 eV可见,随n↑⇒E n↑,∆E n↓*玻尔的理论是半经典的量子论:对于电子绕核的运动,用经典理论处理;对于电子轨道半径,则用量子条件处理。
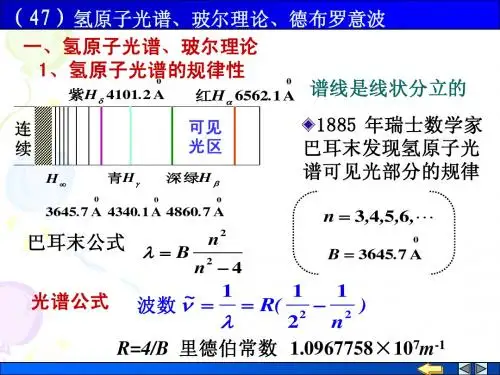


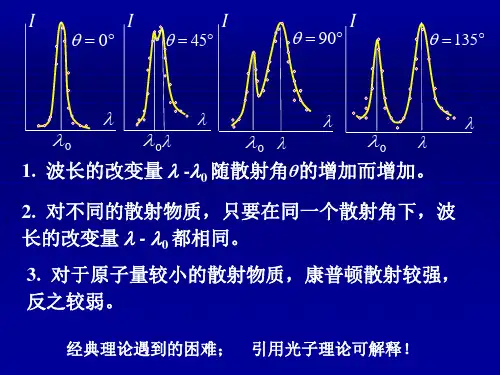
1第4节 氢原子光谱 玻尔理论一、 氢原子光谱,422-=n n B λ∞=,,5,4,3 nA =7.3645B αH βH γH ∞H ,∞→nB =∞λ巴耳末系,:线系极限∞H =:线系极限波长B =∞λA 7.3645波数:沿波线单位长度内波的个数 ν~cνλν==1~λ )121()121(441(1411~2222222nR n B n B n n B -=-=-=-==λν,5,4,3=n 里德伯公式:里德伯恒量1710096776.14-⨯==m BR 帕邢系:, )131(1~22n R -==λν,6,5,4=n 原子光谱实验规律:“原子光谱都是彼此分立的线状光谱,每一条光谱线的波数由 两个光谱项的差值决定” 里兹并合原理,, )()(~n T k T -=νN k n ∈,k n >、:光谱项)(k T )(n T 氢原子:,2)(k R k T =2)(nRn T =碱金属原子:,2)()(α+=k R k T 2)()(β+=n Rn T 、都给定,给出一条光谱线的波数k n 一定,所有的取值对应的谱线构成一个谱线系 k n 不同,给出不同的谱线系 k二、 玻尔理论1、 原子的有核模型1911,卢瑟夫,粒子散射实验α 有核模型 与经典理论矛盾 按照经典理论: 原子光谱应是连续的,原子是不稳定的2、 玻尔的氢原子理论c2(1) 定态假设:原子只能处在一系列具有不连续能量的 稳定状态:定态,不辐射电磁波 定态1, 定态2,,, , 1E 2E , 轨道1, 轨道2, ,(2) 跃迁假设:的定态的定态 n E →k E 光子频率 hE E nk -=ν <,吸收一个光子,>,放出一个光子n E k E n E k E (3)角动量量子化假设:电子绕核转动的角动量:, n hnL ==π2 ,3,2,1=n:量子数n :约化普朗克常数,SI :=π2h = π2h= Js 341005.1-⨯三、 氢原子结构和氢原子光谱 1、 轨道半径(1) 20224r e r V m πε= (2),n mVr L == ,3,2,1=n (,)V m r P r L⨯=⨯=θθsin sin rmV rP L == ,, 222023141 n r e mr πε=22204n me r ⋅= πε ,3,2,1=n , 1=nA ==529.042201mer πε ,2=n 2122⋅=r r ,3=n2133⋅=r r21n r r n ⋅=<<<321r r r :玻尔半径A =529.01r 结论:电子的轨道半径是量子化的 2、 定态能量,, r e mV E 022421πε-=20224r e r V m πε=r e mV 022821πε= ,210202188n r e re E ⋅-=-=πεπε ,3,2,1=nVm e3,,,1=n eV r e E 6.1381021-=-=πε2=n eV E E 4.32/212-== ,,3=n ,51.13/213eV E E -== 21/n E E n =<<<321E E E 的定态:基态,的定态,激发态 1=n 1>n 结论:氢原子的定态能量是量子化的 每一个定态能量称为一个能级∞=n4=n51.1-3=neV 4.3-2=neV 6.13-1=n3、 氢原子光谱氢原子 ,n E →k E k n >辐射光子频率==h E E k n -=ν)(12121k E n E h -)11(221nk h E -- 波数, ==c νν~11(221n k hc E --k n > 令,, hc E R 1-===λν1~)11(22n k R -k n >= hcER 1-=1710097373.1-⨯m 例:赖曼系中波长最短的谱线光子能量是多少? 答:eV 6.13例:巴耳末系中波长最短的谱线光子能量是多少? 答:eV 4.3例:写出氢原子光谱各谱线系的极限波数表达式解:,, ==λν1~11(22n k R -∞→n 2)(~k R =∞ν赖曼系 (), = 1=k R =∞)(~赖ν1710097.1-⨯m 巴耳末系(), 2=k 1710274.04)(~-⨯==∞m R 巴ν5=n 赖曼系4四、 玻尔理论的缺陷氢原子及 类氢离子光谱 , ,, H +He +2Li +3Be Z= 1, 2, 3, 4碱金属元素的原子光谱,光谱的精细结构 塞曼效应,谱线宽度、强度、偏振逻辑上,玻尔理论自相矛盾 认识原子结构的里程碑 “定态”、“能级”、“跃迁” 例:氢原子由量子数为的定态()的定态 n →1-n 求:(1)辐射光子频率1-→n n ν (2)很大时,n 1-→n n νn ν≈:电子在第轨道上的转动频率n νn 解:(1)= 1-→n n ν22121211)1(12])1([1n n n h E n E n E h h E E n n --⋅-=--=--= ()22102)1(128n n n h r e --⋅πε10218r e E πε-= (2)= () n νn n n n n r mV mV r V ππ222=20224nn n r e r V m πε== (,) 31020214214nh r e n r e n ⋅=⋅πεππε n r mV n n =21n r r n ⋅= 很大时,== n 1-→n n ν22102)1(128n n n h r e --⋅πε310214nh r e ⋅≈πεn ν对应原理:当量子数很大时,量子方程应过渡到经典方程 n 经典理论是量子理论在很大时的极限 n 例:氢原子某谱线系的极限波长为,其中一条谱线A 3647 波长为A 6565求:该谱线对应的氢原子初态和末态的能级能量 ()1710097.1-⨯=m R 解:,,, ==λν1~11(22n k R -∞→n 21k R =∞λ2==∞λR k ,,= =λ1)121(22n R -221211n R -=λR nλ14112-=R R λλ44-344=-=R Rn λλ 初态,3=n eV E E 51.13/213-==末态,2=n eV E E 4.32/212-==。


氢原子吸收光谱氢原子的吸收光谱是指氢原子在吸收外部能量后发生能级跃迁时所产生的光谱。
氢原子的吸收光谱提供了深入了解氢原子内部结构和能级之间的跃迁过程的重要信息。
下面是关于氢原子吸收光谱的一般性信息:1. 氢原子能级结构:氢原子的能级结构是由一系列电子能级组成的,这些能级包括基态(最低能级)和激发态(高能级)。
电子可以通过吸收或发射光子来从一个能级跃迁到另一个能级。
2. 玻尔模型:尼尔斯·玻尔提出的玻尔模型是描述氢原子能级的经典模型。
根据这个模型,氢原子的能级与电子的轨道半径有关,而电子在这些轨道上只能具有特定的能量。
3. 布喇格方程:布喇格方程描述了波的性质,包括电子波函数。
通过求解布喇格方程,可以得到氢原子的允许能级。
4. 吸收光谱的产生:当氢原子吸收外部能量时(例如光子),电子会从低能级跃迁到高能级。
这个跃迁的过程伴随着光的吸收,产生吸收光谱。
5. 巴尔末系列:氢原子的巴尔末系列是指电子从高能级跃迁到第二能级(n=2)时产生的谱线。
巴尔末系列包括巴尔末α、巴尔末β等。
6. 朗道-卢瑟福散射:朗道-卢瑟福散射是研究原子结构的重要实验方法。
通过测量散射光的角度和能量,可以推断出原子的内部结构。
7. 量子力学描述:量子力学提供了对氢原子能级和电子跃迁的更精确描述。
薛定谔方程是描述氢原子体系的基本方程。
8. 氢光谱学的应用:氢光谱学的研究不仅提供了对氢原子内部结构的理解,还为分析其他原子和分子的光谱学提供了基础。
结论:氢原子吸收光谱的研究对于理解原子结构、光谱学基础和量子力学等领域都有重要的意义。
通过分析吸收光谱,科学家们能够深入探讨原子内部的能级跃迁过程,为量子理论的发展和实验技术的进步提供了关键信息。
三、玻尔原子理论对氢光谱的解释教学目的:◆了解玻尔原子理论的成功之处及局限性1、 知道巴耳末公式2、 了解如何用玻尔原子理论解释氢原子光谱3、 了解玻尔理论的局限性。
教学重点:玻尔原子理论对氢光谱的解释教学过程:(一) 组织教学(二) 复习提问1、玻尔原子理论的内容是什麽?2、玻尔原子理论中计算氢原子电子的各条可能轨道的半径和电子在各条轨道上运动时的能量公式是什麽?1212121E E h E n E r n r n n -===ν (三) 引入:看课本彩图4,找氢原子光谱在可见光区的四条谱线波长:mH mH mH mH μμμμδγβα4101.04340.04861.06562.0(四) 新授1、 氢光谱的实验规律:即巴耳末公式:⎪⎭⎫ ⎝⎛-=221211n R λ, n=3,4,5,┅┅ 其中λ是氢原子光波的波长,R 为里德伯常量实验值为R=1.096776×107m -12、 玻尔理论导出的氢光谱规律:按玻尔的原子理论,氢原子的电子从能量较高的轨道n 跃迁到能量较低的轨道2时辐射出的光子能量:2E E h n -=ν 但:212212,E E n E E n ==, 由此可得: ,121221⎪⎭⎫ ⎝⎛--=n E h ν 由于λνc=,所以上式可写作:⎪⎭⎫ ⎝⎛--=2211211n hc E λ,此式与巴耳末公式比较,形式完全一样,里德伯常量17110097373.1-⨯=-=m hc E R 与实验符合的很好。
由此可知,氢光谱的巴耳末线系是电子从 n=3,4,5,6,等能级跃迁到n=2的能级时辐射出来的。
玻尔原子理论还解释了帕邢系(在红外区),预言了当时未发现的氢原子的其他光谱线系。
氢原子能级图3、 玻尔理论的局限性(1) 玻尔原子模型在解释氢原子光谱上获得成功,而对核外电子较多的原子,理论与实验相差很多,玻尔理论不再成立,取而代之的是量子力学。
(2) 玻尔理论的成功之处在于它引入了量子的观念,失败之处在于它保留了过多的经典物理理论。