高等数学二重积分图形
- 格式:ppt
- 大小:2.71 MB
- 文档页数:104




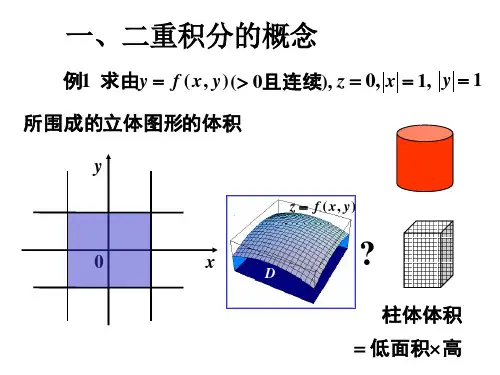

二重积分的计算及几何意义的可视化解释-图解高等数学-下1712.1 二重积分将一元函数积分推广来看对于连续函数f(x,y) 如何求二重积分. 每个二重积分都可以方便地用定积分的方法分步进行计算.矩形区域上的二重积分设f(x,y) 在矩形区域R: a当网格不断进行细分使?x 和?y 都趋近零时, 则趋于R 的面积趋近于极限值, 则称该极限值为f 在R 上的二重积分, 记为:值得注意的是f 函数的连续性是二重积分存在的一个充分条件, 对于许多不连续的函数, 该极限也存在.二重积分的性质连续函数的二重积分也有一些代数性质:二重积分的几何意义当f(x,y) 为正函数时, 则可以把矩形区域R 上的f 函数二重积积分视为曲面为z=f(x,y) 的棱柱体的体积.计算二重积分的Fubini 定理现在计算xy 平面内矩形区域R :0也就是说体积可以这样计算出来: 先固定x, 将4-xy 先关于y 从y=0 到y=1, 然后再对所得x 的表达式关于x 从x=0 到x=2 积分. 则体积可以写成表达式:上述表达式称为二重积分或累次积分(iterated integral).Guido Fubini(圭多.富比尼) 在1907年证明了矩形域上任意一个连续函数的二重积分都可以用两种累次积分的任一种次序计算.有界非矩形区域上的二重积分函数f(x,y) 在非矩形区域R 上的二重积分, 设想被网格覆盖, 不过在R 内的小块面积为红色, 如下图所示:可以看到随着网格不断细分, R内包含的小矩形方块越来越趋于零时, S 就会有极限, 则称该极限为f 在R 上的二重积分:如果f(x,y) 为正, 且在R 上连续, 则曲面z=ff(x,y) 与R 之间的立体趋于的体积为:观看下面的动画:在xy 平面内, 如果R 是一个由两条曲线g1(x) 和g2(x) 围城的区域. 则也可以用切片法来求体积. 先计算截面面积A(x):然后再对A(x) 从x=a 到x=b 作积分可以求得体积:观察下面动画A(x) 从x=a 到x=b 作积分的过程:。

二重积分的计算方法在高等数学中,二重积分是一个重要的概念,它在许多领域都有着广泛的应用,比如物理学、工程学、经济学等。
理解和掌握二重积分的计算方法对于解决相关的实际问题和理论研究都至关重要。
二重积分的定义是在平面区域上对函数进行积分。
直观地说,它可以用来计算平面区域上某个量的总和,比如平面薄片的质量、平面区域的面积等。
那么,如何计算二重积分呢?常见的计算方法主要有直角坐标法和极坐标法。
直角坐标法是我们最常接触的方法之一。
当积分区域是由直线边界围成的矩形、三角形或者其他简单形状时,直角坐标法往往比较适用。
我们先来看 X 型区域。
如果积分区域可以表示为\(a\leq x\leqb\),\(\varphi_1(x)\leq y\leq \varphi_2(x)\),那么二重积分可以写成:\\int\!\!\int_D f(x,y) d\sigma =\int_{a}^{b}dx \int_{\varphi_1(x)}^{\varphi_2(x)} f(x,y) dy\这里要先对\(y\)积分,再对\(x\)积分。
再来看 Y 型区域。
如果积分区域可以表示为\(c\leq y\leq d\),\(\psi_1(y)\leq x\leq \psi_2(y)\),那么二重积分可以写成:\\int\!\!\int_D f(x,y) d\sigma =\int_{c}^{d}dy \int_{\psi_1(y)}^{\psi_2(y)} f(x,y) dx\在使用直角坐标法计算二重积分时,关键是要正确确定积分区域的类型,以及积分的上下限。
接下来我们说一说极坐标法。
当积分区域具有圆形、扇形或者是与圆相关的形状时,极坐标法通常会更加简便。
在极坐标系中,点用\((\rho,\theta)\)表示,其中\(\rho\)表示点到原点的距离,\(\theta\)表示极角。
如果积分区域可以表示为\(\alpha\leq\theta\leq\beta\),\(\varphi_1(\theta)\leq\rho\leq\varphi_2(\theta)\),那么二重积分可以写成:\\int\!\!\int_D f(x,y) d\sigma =\int_{\alpha}^{\beta}d\theta \int_{\varphi_1(\theta)}^{\varphi_2(\theta)} f(\rho\cos\theta,\rho\sin\theta)\rho d\rho\在极坐标法中,要注意\(\rho\)的积分上下限以及函数在极坐标下的表达式。


二重积分圆心不在原点的圆引言积分是高等数学中的一个重要概念,也是解决很多实际问题的工具之一。
在二重积分中,我们可以通过求解曲线与坐标平面之间的面积来推导出各种数学物理问题的解。
本文将重点讨论二重积分中圆心不在原点的圆的问题。
圆的参数方程圆可以用参数方程来表示,对于圆心(x0, y0)和半径R的圆,其参数方程可以表示为:x = x0 + R * cosθy = y0 + R * sinθ其中,θ为参数,表示圆的角度。
圆心不在原点的圆的二重积分在二重积分中,我们考虑圆心不在原点的圆的情况。
为了求解这种情况下的二重积分,我们可以考虑利用坐标变换来将圆心移动到原点。
极坐标变换极坐标变换是常用的二维坐标变换方法之一。
其基本思想是将平面上的点表示为极径(r)和极角(θ)的形式,通过极坐标变换可以将二重积分问题转化为极坐标下的简单形式。
极坐标下圆心移动到原点的变换对于圆心为(x0, y0)、半径为R的圆,我们可以通过平移坐标系的方法将圆心移动到原点,在极坐标下,原来的圆方程变为:r = R利用极坐标变换求解二重积分我们以求解圆心不在原点的圆的面积为例,来讨论如何利用极坐标变换来求解二重积分。
步骤一:坐标变换设新的变量为(r,θ),则原坐标系下的面积元素dA可以通过极坐标与直角坐标的关系求得:dA = r * dr * dθ步骤二:确定积分范围在极坐标下,圆心为原点的圆可以表示为:0 ≤ r ≤ R0 ≤ θ ≤ 2π步骤三:求解二重积分利用极坐标变换后,原来的二重积分就变为:∬f(x, y) dA = ∫∫f(r * cosθ, r * sinθ) * r dr dθ圆心不在原点的圆的实例下面通过两个实际的例子,进一步说明如何求解二重积分中圆心不在原点的圆的问题。
实例一:求解圆形区域的面积我们考虑一个圆心为(2, 1)、半径为3的圆,需要计算圆形区域的面积。
(1)坐标变换利用极坐标变换将圆心移动到原点,可得新的变量为(r,θ),其中θ的范围为0到2π,r的范围为0到3。