水力学例题
- 格式:doc
- 大小:1.62 MB
- 文档页数:43
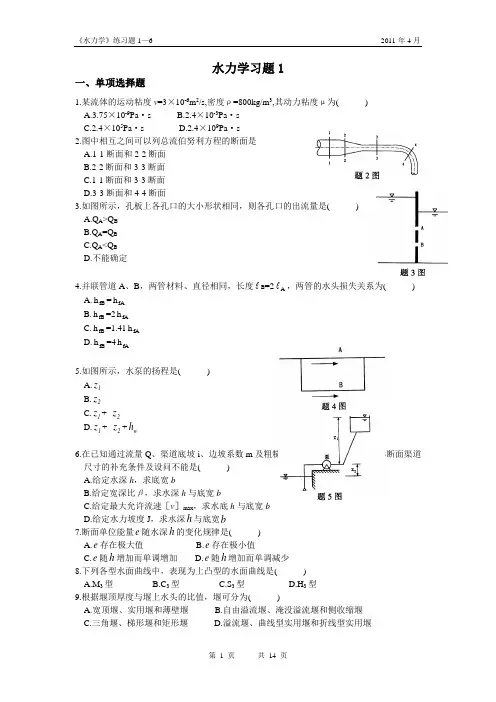
水力学习题1一、单项选择题1.某流体的运动粘度v=3×10-6m2/s,密度ρ=800kg/m3,其动力粘度μ为( )A.3.75×10-9Pa·sB.2.4×10-3Pa·sC.2.4×105Pa·sD.2.4×109Pa·s2.图中相互之间可以列总流伯努利方程的断面是A.1-1断面和2-2断面B.2-2断面和3-3断面C.1-1断面和3-3断面D.3-3断面和4-4断面3.如图所示,孔板上各孔口的大小形状相同,则各孔口的出流量是( )A.Q A>Q BB.Q A=Q BC.Q A<Q BD.不能确定4.并联管道A、B,两管材料、直径相同,长度 B=2 A,两管的水头损失关系为( )A.hfB =hfAB.hfB =2hfAC.hfB =1.41hfAD.hfB =4hfA5.如图所示,水泵的扬程是( )A.z1B.z2C.z1+ z2D.z1+ z2+h w6.在已知通过流量Q、渠道底坡i、边坡系数m及粗糙系数n的条件下,计算梯形断面渠道尺寸的补充条件及设问不能是( )A.给定水深h,求底宽bB.给定宽深比β,求水深h与底宽bC.给定最大允许流速[v]max,求水底h与底宽bD.给定水力坡度J,求水深h与底宽b7.断面单位能量e随水深h的变化规律是( )A.e存在极大值B.e存在极小值C.e随h增加而单调增加D.e随h增加而单调减少8.下列各型水面曲线中,表现为上凸型的水面曲线是( )A.M3型B.C3型C.S3型D.H3型9.根据堰顶厚度与堰上水头的比值,堰可分为( )A.宽顶堰、实用堰和薄壁堰B.自由溢流堰、淹没溢流堰和侧收缩堰C.三角堰、梯形堰和矩形堰D.溢流堰、曲线型实用堰和折线型实用堰10.速度v、长度l、运动粘度v的无量纲组合是( )A.vlv2B.v lv2C.v lv22D.vlv二、填空题(不写解答过程,将正确的答案写在每小题的空格内。

45sin 3sin 311α闸门右侧水压力:kN b h gh P 74.27145sin 228.9100021sin 21222=⨯⨯⨯⨯⨯=⋅=αρ 作用点:m h h 943.045sin 32sin 32'2===α 总压力大小:kN P P P 67.3474.2741.6221=-=-=对B 点取矩:'D '22'11Ph h P h P =-'D 67.34943.074.27414.141.62h =⨯-⨯m h 79.1'D =作用在闸门上的总压力的作用点距离闸门下端的距离是1.79m 。
2. 一弧形闸门如图所示,闸门宽度b=1m ,圆心角φ=45°,水头h=3m 。
求水对闸门的静水总压力及方向。
[解] 水平分力:kN b h h g A gh F x c px 145.4432.381.910002=⨯⨯⨯=⋅⨯==ρρ压力体体积:322221629.1)45sin 3(8]321)345sin 3(3[)45sin (8]21)45sin ([b m h b h h hh V =-⨯+-⨯=-+-=ππ 铅垂分力:kN gV F pz 41.111629.181.91000=⨯⨯==ρ合力:kN F F F pz px p 595.4541.11145.442222=+=+=方向:5.14145.4441.11arctanarctan===pxpz F F θ3. 图示管路由两根不同直径的管子与一渐变连接管组成。
已知d A =200mm ,d B =400mm ,A 点相对压强P A =68.6kPa ,B 点相对压强P B =39.2kPa ,B 点的断面平均流速v B =1m/s ,A 、B 两点高差△z=1.2m 。
试判断流动方向,并计算两断面间的水头损失hw 。
[解] B B A A v d v d 2244ππ=s m v d d v B A B A /41)200400(222=⨯==∴假定流动方向为A →B ,则根据伯努利方程w BB B B A A A A h gv g p z g v g p z +++=++2222αραρ其中z z z A B ∆=-,取0.1≈=B A ααz gv v g p p h BA B A w ∆--+-=∴222ρ2.1807.92149807392006860022-⨯-+-=056.2>=m故假定正确。

水力学练习题水力学练习题水力学是研究液体在不同条件下的运动和力学性质的学科。
它在工程领域中有着广泛的应用,涉及到水的供应、排水系统设计、水坝和水电站等方面。
在学习水力学的过程中,练习题是提高理论知识和解决实际问题的有效方法。
本文将通过一些水力学练习题,帮助读者更好地理解和应用水力学的知识。
题目一:流量计算某水厂的进水管道直径为0.5米,流速为2米/秒。
请计算该管道的流量。
解析:流量是单位时间内通过某一横截面的液体体积。
根据流量的定义,我们可以通过以下公式计算流量:Q = A × V其中,Q表示流量,A表示横截面积,V表示流速。
根据题目中的数据,进水管道的直径为0.5米,半径为0.25米。
横截面积可以通过圆的面积公式计算:A = π × r²代入数据,得到横截面积为0.19634954084936207平方米。
流速为2米/秒,代入公式,得到流量:Q = 0.19634954084936207平方米× 2米/秒Q = 0.39269908169872414立方米/秒因此,该管道的流量为0.39269908169872414立方米/秒。
题目二:水头计算某水坝的高度为50米,水面距离坝顶的高度为40米。
请计算水的压力。
解析:水的压力是由于水的重力作用而产生的。
根据水的压力公式,我们可以通过以下公式计算水的压力:P = ρ × g × h其中,P表示压力,ρ表示水的密度,g表示重力加速度,h表示水的高度。
根据题目中的数据,水的高度为40米。
代入公式,我们需要知道水的密度和重力加速度。
水的密度一般取998千克/立方米,重力加速度取9.8米/秒²。
代入公式,得到水的压力:P = 998千克/立方米× 9.8米/秒² × 40米P = 392720帕斯卡因此,水的压力为392720帕斯卡。
题目三:水流速度计算某水流的流量为0.2立方米/秒,管道直径为0.3米。

水力学题(完整资料).doc【最新整理,下载后即可编辑】⒈在倾角θ=30°的斜面上有一厚度为δ=0.5 mm的油层。
一底面积A=0.15m2,重G=25N的物体沿油面向下作等速滑动,如图所示。
求物体的滑动速度u 。
设油层的流速按线性分布,油的动力粘度μ=0.011 N·s/ m2。
2.有一与水平面成倾斜角α=60°的自动翻版闸门,如图所示。
当上游水深超过h1= 2.5m,下游水深h2= 0.5m时,闸门便自动开启。
求翻板闸门铰链的位置l值。
(不计摩擦力和闸门自重)3.有一水电站的水轮机装置,如图所示。
已知尾水管起始断面1的直径d=1 m ,断面1与下游河道水面高差h=5 m。
当通过水轮机的流量Q=1.5 m3/s 时,尾水管(包括出口)水头损失h=1.5m 。
求断面1的动水压强。
4.某渠道在引水途中要穿过一条铁路,于路基下修建圆形断面涵洞一座,如图所示,已知涵洞设计流量(即渠道流量)Q=1 m3/s ,涵洞上下游允许水位差z =0.3 m ,涵洞水头损失1h ω =1.4722v g (v 为洞内流速)。
涵洞上下游渠道流速极小。
求涵洞直径d 。
5.图示一从水库引水灌溉的虹吸管,管径d=10 cm ,管中心线的最高点B 高出水库水面2 m 。
管段AB (包括进口)的水头损失AB h ω=3.522v g ,管段BC 的水头损失BC h ω=1.522v g (v 为管中流速)。
若限制管道最大真空高度不超过6 m 水柱,问:(1)虹吸管引水流量量有无限制?如有,最大值为多少?(2)水库水面至虹吸管出口的高差h 有无限制?如有,最大值为多少?B6.有一大水箱,水箱面积很大,下接一管道,如图所示。
已知大管和收缩段管径分别为d 1=5 cm 和d 2=4 cm ,水箱水面与管道出口中心点的高度差H =1 m 。
如不计水头损失,问容器A 中的水是否会沿管B 上升?如上升,上升高度h 为若干?7.有一从水箱引水的管道如图所示。

水力学习题及答案水力学习题及答案一、选择题1、下列哪个参数不是水动力学的研究对象? A. 流量 B. 速度 C. 压力 D. 重量2、一根水平放置的管道,两端开口,当一端进水,另一端出水时,其流速与流量之间的关系为? A. 反比关系 B. 正比关系 C. 不相关 D. 无法确定3、一水坝的形状为抛物线形,其水头高度为30米,底部宽度为50米,则水坝的顶部的宽度为? A. 10米 B. 20米 C. 30米 D. 40米4、在没有特殊说明的情况下,通常情况下,所说的水密度是指? A. 在4摄氏度时的密度 B. 在100摄氏度时的密度 C. 在常温常压下的密度 D. 在海平面的平均密度二、简答题5、请简述水动力学的基本研究方法和主要应用领域。
51、请描述层流和湍流的定义,并解释它们在流体运动中的区别。
511、请阐述水头损失的物理意义和计算方法。
5111、对于一个给定的管径和流速,如何计算管道的流量?请给出计算公式并解释每个公式的物理意义。
三、综合题9、通过数值模拟方法研究流体运动时,有哪些可能遇到的困难和挑战?如何解决这些困难和挑战?91、假设在一个直径为1米的管道中流动的水,其平均流速为1米/秒。
请计算该管道的流量。
再假设在该管道的入口处加入一个水泵,使得管道内的流速增加到2米/秒,请问流量是否会翻倍?为什么?答案:一、选择题1、D。
水动力学主要研究的是流体(包括水)的运动状态和规律,不涉及物体的重量。
因此,重量不是水动力学的研究对象。
2、B。
根据伯努利定理,在不可压缩的稳定流场中,流速与流量成正比。
因此,流速与流量之间存在正比关系。
3、A。
根据抛物线的几何性质,抛物线的顶点位于其对称轴上。
因此,水坝顶部的宽度为底部的1/2,即25米。
又因为题目中给出的底部宽度为50米,所以水坝顶部的宽度为10米。
因此,答案为A。
4、C。
在工程应用中,通常所说的水密度是指常温常压下的密度。
因此,答案为C。
二、简答题5、水动力学的基本研究方法是基于物理学和数学的流体动力学理论和实验方法,研究流体运动的规律和特性。

Equation Chapter 1 Section 1应用流体力学第一章例1-1 20℃体积为2.5立方米的水,党温度升高到80℃时,其体积增加多少?例1-2 若要是水的体积减少0.1%、1%.则应使压强增加多少?已知水的体积模量K 为2000MPa 。
例1-3 输水管长L=200m,直径d=0.4m 。
做水压实验,使管中压强达到5.39×106Pa 后停止加压,经历1h 管中压强降到4.90×106Pa 。
如不计管道变形,问在上述情况下,经管道漏缝流出的水量平均每秒是多少?水的压缩率为k=4.83×10-10Pa 。
例1-4 试绘制平板间液体的流速分布图与切应力分布图,设平板间上、下液体的流速分布均为直线分布。
已之上层液体粘度为µ1,液层高度为h1,下层液体高度为µ2,液层高度为h2,平板流速为U,如图1-3a 所示。
例1-5 一底面积为0.40.45平方米、高为0.01m 的木板,质量为5Kg ,沿着涂有润滑油的斜面向下做等速运动,如图1-4所示。
已知木块运动速度µ=1m/s,油层厚度£=0.1mm,由木块所带动的油层运动速度呈直线分布,试求油的粘度。
例1-6 直径R=0.1m 的圆盘,由轴带动在一平台上旋转,圆盘与平台间有厚度§=1.5mm 的油膜,当圆盘以n=50r/min 旋转时,测得扭矩M=2.94×10-4N.m 。
设油膜内速度沿垂直油膜方向为线性分布,试确定油的粘度及圆盘边缘的切应力t 。
思考题1-1 何谓流体连续性模型?含有旗袍的液体是否适用连续介质模型?1-2 为什么水通常被认为不可压缩流体?1-3 流体区别于固体的重要特性是什么?1-4 流体粘度与哪些因素有关?它们随温度如何变化?它对流体有何影响?1-5 牛顿流体的t 与du/dy 的关系曲线有一固定斜率,那么t 与du/dy 的关系曲线有固定斜率的流体一定是牛顿流体?1-6 理想流体是指以下哪种流体? A 无粘性流体 B 完全不可压缩流体 C 无粘性完全不可压缩流体。

第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5.已知液体中流速沿y 方向分布如图示三种情况,试根据牛顿内摩擦定律yud d μτ=,定性绘出切应力沿y 方向的分布图。
[解]1-6.为导线表面红绝缘,将导线从充满绝缘涂料的模具中拉过。

水力学一、单项选择题1. 图示圆管所受到的单位长度上静水总压力垂直分力的大小是: ()A.17.3kNB.34.7kNC.52kND.69.4kN2. 在静止液体中,静水压强的方向总是()A、倾斜指向受压面B、平行于受压面C、垂直指向受压面D、背离受压面3. 图示垂直置于水中的矩形平板闸门,宽度b=1m,闸门高h=3m,闸门两侧水深分别为,,总压力作用点距闸门底部的铅直距离为: ()A.2.5mB.1.5mC.2mD.1m4. 粘性流体测压管水头线的沿程变化是()A.沿程上升B.沿程下降C.保持水平D.以上情况均有可能5. 测量水槽中某点水流流速的仪器有()A、文丘里计B、毕托管C、测压管D、薄壁堰6. 恒定流具有下列哪种性质()。
A.当地加速度∂u/∂t=0B.迁移加速度∂u/ ∂S=0C.当地加速度∂u/∂t≠0D.迁移加速度∂u/ ∂S≠07. 沿程水头损失与断面平均流速的一次方成正比的水流属()A.层流区B.紊流水力光滑区C.紊流过渡区D.紊流水力粗糙区8. 某一圆形有压油管的直径为d=150mm,流速为v=0.256m/s,长1km,雷诺数1921,其沿程损失为()A.74.25cm油柱B.74.25cm水柱C. 95.26cm油柱D. 62.26cm油柱9. 圆管层流的流速是如何分布的()A.直线分布 B.抛物线分布C.对数曲线分布D.双曲线分布10. 长管并联管道,若管长管径,粗糙度均布相等,但其下述哪个因素相等?()A 水头损失相等B 通过流量相等C 总的能量损失相等D 水力坡度相等11. 串联长管如图所示,通过流量为Q=50L/s,管道阻抗分别为,则水头H为()A 15.64mB 13.53mC 12.72m D14.71m12. 突然放大管道尺寸同上题,若已知放大前断面平均流速为4m/s,则局部水头损失为()A 0.256mB 0.347mC 0.612mD 0.459m13. 明渠水力最佳矩形断面的宽深比是:()A.0.5B.1.0C.3D.214. 具有任意断面形状的均匀流的沿程水头损失有以下哪些特性?()与流程长度成正比,与壁面平均切应力、水力半径成反比与壁面平均切应力成正比,与流路长度、水力半径成反比与流路长度,水力半径成正比,与壁面平均切应力成反比与流路长度、平均切应力成正比,与水力半径成反比15. 有压管道的管径d与管流水力半径的比值d /R=()A.8;B.4;C.2;D.1。


水力学练习题水力学是研究液体运动规律及其与固体边界相互作用的科学,以下是一些水力学练习题,供学习者练习:1. 静水压力计算某容器底部受到的静水压力为2.4×10^5 Pa,求该容器底部的深度。
2. 伯努利方程应用在一水平管道中,水的流速从2 m/s增加到4 m/s,假设管道的横截面积保持不变,求水的压强变化。
3. 流速和流量的计算已知一河流的横截面积为50 m²,流速为1.5 m/s,求该河流的流量。
4. 雷诺数的计算某管道内水流的直径为0.2 m,流速为2 m/s,水的密度为1000kg/m³,动力粘度为0.001 Pa·s,求该水流的雷诺数。
5. 临界雷诺数的判断给定一管道内水流的雷诺数为2000,判断该水流是层流还是湍流。
6. 水头损失计算在一长为100 m,直径为0.5 m的管道中,水以2 m/s的速度流动,求沿程水头损失。
7. 孔口出流问题一个圆形孔口的直径为0.1 m,水从孔口自由出流,求出流速度和出流量。
8. 明渠流的计算某明渠的底部宽度为2 m,水深为1 m,流速为1 m/s,求明渠的流量和水力半径。
9. 水跃现象分析在一宽为4 m的矩形渠道中,水从上游以2 m/s的速度流入,下游水深为0.5 m,分析是否会产生水跃,并计算水跃的位置。
10. 水力梯度线和能量梯度线在一倾斜的管道中,水流速度从上游的1 m/s增加到下游的2 m/s,求水力梯度线和能量梯度线的变化。
11. 水轮机效率计算已知一水轮机的输入功率为100 kW,输出功率为80 kW,求该水轮机的效率。
12. 泵的扬程计算某泵的流量为50 m³/h,功率为15 kW,求该泵的扬程。
13. 波浪理论应用在一开放海域,波浪高度为 2 m,周期为10 s,求该波浪的波长。
14. 潮汐能计算某海域的潮汐高度差为5 m,平均流速为1 m/s,求该海域的潮汐能。
15. 流体静力学平衡问题一圆柱形容器内装满水,水的深度为3 m,求容器底部的静水压力。
典型例题【例1】两个平行固定边壁间距为25mm,中间为粘滞系数为μ=0.7Pa·s的油,有一的平板(该平板厚1mm),在距一个边壁4mm的距离处以的速度拖行。
设平板与边壁完全平行,并假设平板两边都系线性流速分布,求拖行平板的力。
【解】由牛顿内摩擦定律,内摩擦力平板两边的流速分布为线性,则平板两边的速度梯度分别为所以由于平板以匀速拖行,因此拖行平板的力F与内摩擦力相等,即:【例2】下图为一溢流坝上的弧形闸门。
已知:R=10m,闸门宽b=8m,。
求作用在该弧形闸门上的静水总压力的大小和方向。
【解】(1)水平分力铅直投影面如图,,方向向右。
(2)铅直分力压力体如图abcde,A cde=扇形面积ode-三角形面积ocd==4.52m2,方向向上。
(3)总压力(4)作用力的方向合力指向曲面,其作用线与水平方向的夹角【例3】如图溢流坝,上游断面水深h 1=1.5m ,下游断面水深h 2=0.6m ,略去水头损失;求水流对2m 坝宽(垂直纸面)的水平作用力。
注:上、下游河床为平底,河床摩擦力不计,为方便计算取ρ=1000kg/m 3,g=10m/s 2。
【解】以1-1与2-2断面及沿坝面(包括上下游部分河床边界)与水流自由表面所围成的空间作为控制体,并取沿水流方向为x 正向。
(1)求上、下游断面的流速以河床为基准面,对1-1与2-2断面写能量方程式因为 p1 = p2 = p , α,1α=2α=1,于是(a )由连续方程得(b)=1.5m ,代入式(a)和(b)将hν=1.83 m/s ,可求得(2)求1-1断面和2-2断面的动水压力(3)计算过水断面的流量(4)沿x方向写动量方程式令坝面对水体的反作用力在水平方向的分力为R,方向向左。
沿x方向的动量方程为所以坝面对水体的反作用力R的方向与所设的方向相同。
水流对坝面的作用力与R大小相等,方向相反。
思考题1.1静水压强有哪些特性?静水压强的分布规律是什么?1.2试分析图中压强分布图错在哪里?1.3何谓绝对压强,相对压强和真空值?它们的表示方法有哪三种?它们之间有什么关系?1.4图示一密闭水箱,试分析水平面A—A,B—B,C—C是否皆为等压面?何谓等压面?等压面的条件有哪些?1.5一密闭水箱(如图)系用橡皮管从C点连通容器Ⅱ,并在A,B两点各接一测压管,问:思 1 . 4 思1 . 5(1)AB两测压管中水位是否相同?如相同时,问AB两点压强是否相等?(2)把容器Ⅱ提高一些后,p比原来值增大还是减小?两测压管中水位变化如何?1.6什么叫压力体?如何确定压力体的范围和方向?习 题1.1 图示为一密闭容器,两侧各装一测压管,右管上端封闭,其中水面高出容器水3 m ,管内液面0p 压强为78 kPa ;左管与大气相通。
求:(1)容器内液面压强c p ;(2)左侧管内水面距容器液面高度h 。
1.2 盛有同种介质(密度==B A ρρ 1 132.6 kg/m 3)的两容器,其中心点A 与B 位于同一高程,今用U 形差压计测定A 与B 点之压差(差压计内盛油,密度=0ρ867.3 kg/m 3 ), A 点还装有一水银测压计。
其他有关数据如图题1.2所示。
问:(1)A 与B 两点之压差为多少?(2)A 与B 两点中有无真空存在,其值为多少?1.3 图示一圆柱形油桶,内装轻油及重油。
轻油密度1ρ为6 632.6 kg / m 3,重油密度2ρ为887.75k g/m 3,当两种油重量相等时,求:(1)两种油的深度1h 及2h 为多少?(2)两测压管内油面将上升至什么高度?1.4 在盛满水的容器盖上, 加上6 154N 的荷载G (包括盖重),若盖与容器侧壁完密合,试求A ,B ,C ,D 各点的相对静水压强(尺寸见图)。
1.5 今采用三组串联的U 形水银测压计测量高压水管中压强,测压计顶端盛水。
当M 点压强等于大气压强时,各支水银面均位于0一0水平面上。
水力学习题集一、流量计算题1.计算一个圆形管道的流量,已知管径为10cm,水速为2m/s。
计算结果保留两位小数。
2.计算一个矩形开放槽的流量,已知槽的宽度为1m,深度为0.5m,水速为1.5m/s。
计算结果保留两位小数。
3.计算一个圆形喷嘴的流量,已知喷嘴的直径为5cm,喷嘴的速度为10m/s。
计算结果保留两位小数。
二、压力计算题1.计算一个容器内的压力,已知容器的高度为2m,距离底部0.5m处的压力为300Pa。
计算结果保留两位小数。
2.计算一个水泵升水到10m高度需要的压力,已知水的密度为1000kg/m^3。
计算结果保留两位小数。
3.计算一个水塔底部的压力,已知水塔的高度为20m,水塔底部的密度为1000kg/m^3。
计算结果保留两位小数。
三、水力计算题1.计算一个水力机械的功率,已知水的流量为10m^3/s,水的高度差为100m。
计算结果保留两位小数。
2.计算一个水电站的发电量,已知水流经发电机的功率为2000kW,水的流量为100m^3/s,发电的时间为10小时。
计算结果保留两位小数。
3.计算一个喷泉的射高,已知喷泉的流量为10m^3/s,喷泉的流速为20m/s。
计算结果保留两位小数。
四、水力参数题1.计算一个水泵的效率,已知输入功率为1000W,输出功率为800W。
计算结果保留两位小数。
2.计算一个水力机械的效率,已知输出功率为400kW,输入功率为500kW。
计算结果保留两位小数。
3.计算一个水泵的扬程,已知输入功率为800W,效率为0.8,流量为0.2m^3/s。
计算结果保留两位小数。
以上是关于水力学习题集的一些例题,通过这些题目的计算,可以帮助大家更好地理解和运用水力学的知识。
希望能对大家的学习有所帮助!。
第1章 绪论例1:已知油品的相对密度为0.85,求其重度。
解:3/980085.085.0m N ⨯=⇒=γδ例2:当压强增加5×104Pa 时,某种液体的密度增长0.02%,求该液体的弹性系数。
解:0=+=⇒=dV Vd dM V M ρρρρρd dV V -= Padp d dp V E p 84105.2105%02.0111⨯=⨯⨯==-==ρρβ例3:已知:A =1200cm 2,V =0.5m/sμ1=0.142Pa.s ,h 1=1.0mm μ2=0.235Pa.s ,h 2=1.4mm 求:平板上所受的内摩擦力F绘制:平板间流体的流速分布图及应力分布图 解:(前提条件:牛顿流体、层流运动)dy du μτ= ⎪⎪⎩⎪⎪⎨⎧-=-=⇒2221110h u h u V μτμτ 因为 τ1=τ2 所以sm h h Vh u h uh u V /23.02112212211=+=⇒=-μμμμμN h uV A F 6.411=-==μτ第2章 水静力学例1:如图,汽车上有一长方形水箱,高H =1.2m ,长L =4m ,水箱顶盖中心有一供加水用的通大气压孔,试计算当汽车以加速度为3m/s 2向前行驶时,水箱底面上前后两点A 、B 的静压强(装满水)。
解:分析:水箱处于顶盖封闭状态,当加速时,液面不变化,但由于惯性力而引起的液体内部压力分布规律不变,等压面仍为一倾斜平面,符合0=+s gz ax 等压面与x 轴方向之间的夹角g a tg =θPaL tg H h p A A 177552=⎪⎭⎫ ⎝⎛⋅+==θγγPaL tg H h p B B 57602=⎪⎭⎫ ⎝⎛⋅-==θγγ例2:(1)装满液体容器在顶盖中心处开口的相对平衡分析:容器内液体虽然借离心惯性力向外甩,但由于受容器顶限制,液面并不能形成旋转抛物面,但内部压强分布规律不变:Cz gr p +-⋅=)2(22ωγ利用边界条件:r =0,z =0时,p =0作用于顶盖上的压强:g r p 222ωγ=(表压)(2)装满液体容器在顶盖边缘处开口的相对平衡压强分布规律:Cz gr p +-⋅=)2(22ωγ边缘A 、B 处:r =R ,z =0,p =0g R C 222ωγ-=作用于顶盖上的压强:()2222r R gp --=ωγ例3:已知:r 1,r 2,Δh求:ω0 解:212120=-s z gr ω (1)222220=-s z gr ω (2)因为 h z z s s ∆==21所以212202r r h g -∆=ω例4已知:一圆柱形容器,直径D =1.2m ,完全充满水,顶盖上在r 0=0.43m 处开一小孔,敞开测压管中的水位a =0.5m ,问此容器绕其立轴旋转的转速n 多大时,顶盖所受的静水总压力为零?已知:D =1.2m ,r 0=0.43m ,a =0.5m 求:n解:据公式 )(Z d z Y d y X d x dp ++=ρ 坐标如图,则 x X 2ω=,y Y 2ω=,g Z -= 代入上式积分:C z gr p +-⋅=)2(22ωγ (*)由题意条件,在A 点处:r =r 0,z =0,p =γa 则 C gr a +-⋅=)02(202ωγγ所以 )2(202gr a C ωγ-⋅=所以 )2()2(20222gr a z gr p ωγωγ-⋅+-⋅= 当z =0时: )2(220222gr a gr p ωγωγ-⋅+=它是一旋转抛物方程:盖板上静压强沿径向按半径的二次方增长。
例题1:如下图所示,一圆锥体绕自身轴线等速旋转,锥体与固定壁面间的距离为K ,空隙全部被动力粘滞系数为μ的牛顿流体所充满。
当旋转角速度为ω,锥体底部半径为R ,高为H ,求作用于圆锥的阻力矩。
解:M=⎰⎰⎰⎰====Kdhr KdA rKdAr Ku dAr322cos 2πμωαπμωωμμτ=HK Rαπμωcos23而22cos RHH+=α;故:M=2232RHKR+⨯πμω例题2:涵洞进口处,装有与水平线成600倾角而边长为1m 的正方形平板闸门(AB=1m ),求闸门所受静水总压力的大小及作用点。
解:坐标只能建在水面上。
A kp p 807.91807.9=⨯=aB kp p 300.18)231(807.9=+⨯=KNp p P BA 050.14112=⨯⨯+=h h Ay I y y C C C C C D 6.160sin 433.112160sin 433.1160sin 121160sin 03=+=⨯⨯+=+=0=D x矩形和圆形的C y 和C I 值矩形:2hy C =123bhI C =圆形:r y C =44rI C π=例题3:一直立矩形闸门,用三根工字梁支撑,门高及上游水深H 均为3m,把此闸门所受静水压强分布图分为三等份,每根工字梁分别设在这三等份的重心,求三个工字梁的位置?解:设静水压力分布图的面积为A ,则每一等份为A/3mh H A h 3,21313211221=∴⨯==γγ mh H A h 45.2,213232212222=∴⨯==γγm h h h h m h h c 091.22718.0121212=-+==-m Ah J h y c xc c 11.2718.0091.212)718.0(091.2322=⨯+=+=mh H h h m h H c 725.2255.02232=-+==-mAh J h y c xc c 73.2725.212)55.0(725.22333=+=+=mh h h h h h h y m h y 11.22)(31,15.1322121121211=++-+===。
mh h h h h h h y 73.22)(3132322323=++-+=例题4:矩形闸门可绕铰轴转动,求证+>h H 1514a 时,闸门在水压力的作用下可以自动开启。
解:当作用点在铰的上方时,闸门在水压力的作用下可以自动开启。
首先求临界状态时即作用点在铰上的H ,设闸门宽为BAy I y y C C C D +=,hBh a H B hh a H y a H D )10(12103--+--==-∴ah H +=∴1514,所以只有当+>h H 1514a 时,闸门在水压力的作用下可以自动开启。
例5:倾角060=α的矩型闸门AB ,上部油深mh 11=,下部水深,22m h =3/800m kg =油ρ,求作用在闸门上每米宽度的总压力及其作用点。
解:g p 66.452960sin 121807.980060sin 12101=⨯⨯⨯=⨯⨯=ρNp 93.4076660sin 2)2298071807.9800(02=⨯⨯+⨯⨯=NP 59.4529693.4076666.4529=+=以B 点为转轴,应用合力矩求作用点,不能用Ay I y y C C C D+=公式求作用点。
GBP AFP yP D⨯++⨯=⋅201/)60sin 23(可把2P 分成两个三角形来求解梯形的重心,以B 点为转轴332//2/22FB PFB P GB P ⨯+⨯=⨯/60sin 3D D y y -=0=D x例6:如下图所示:自由表面的压强2/0/40.117m kN p = , 当地大气压的绝对值为 2//07.98m kN p a=。
求水对AB 平板的总压力P 。
解:把外压强折合成水的测压管高度后再进行计算mgp p a97.1//0=-ρ,坐标建在水面上 1.97m 处。
mgp p y ac27.23.0//0/=+-=ρkN A gy A p P c c 68.6/===ρm bhAy I y yc c cD28.25.06.027.21227.23///=⨯⨯+=+=作用点mgpp y aD31.028.2//0=--=ρ,0=Dx ,作用点在水面下0.31m 处。
P 垂直指向AB 平板。
例7:有一ABC 三角形受压面,可绕AB 轴旋转,见下图,求水对闸门的总压力的大小、方向、作用点及总压力对AB 轴的力矩。
解:1)求水对闸门的总压力P : 因为三角形的重心c h 在水面下32h 处,所以:①P的大小:P=32322bh g hb h g A gh c ρρρ=⋅=②作用点:bdyhy xdy dA ==b hbdy hydA y J Ahx 4332===⎰⎰43232h bh h J Ay J y x c x D =⨯==bdyh y gygydA pdA dP ρρ===因为:⎰=AD xdP P x所以:bPbhgPdyb hy g PbdP hyPxdP x hhAD 434222230=====⎰⎰⎰ρρ③P 的方向:垂直指向闸门。
2)求对AB 轴的力矩M :M=2)(0x xdy p p ha ⋅-⎰ 因为gyp p a ρ=-yh b x =所以82)(2202hgb dy y hbgy M hρρ==⎰例8:求压力体例9:圆柱体外径d=2.00m,长L=5.00m,放置在与水平面成060角的斜面上,圆柱体与斜面的接触线在水面下水深m h 00.1=处。
求圆柱体所受静水总压力及其与水平面所构成的交角α。
解:200.500.500.1mm m A x =⨯=,kNghAP xx 52.2400.5211007.981=⨯⨯⨯==-ρ压力体V 为右上方一个三角形棱柱体V 1加上左下方一个半圆柱面V 2,方向朝上。
kN PP P zx98.12122=+=40.78tan ==xz P P ar αm R h D 98.0sin ==α(水面下)。
例10:图示为一封闭容器,垂直于纸面宽b=2.000m,AB 为一1/4半径为m R 000.1=的圆弧闸门,闸门A 处设一铰轴。
容器内BC 线kNR siin d gL V V g gV P z 49..119]2230cos 30[)(2221=+=+==πρρρ以上为油,密度/ρ为0.33/10800m kg ⨯,BC 线以下为水。
U 形测压计中左侧液体密度//ρ为33/10000.3m kg ⨯,求B —B 点处力F 为多大 时才能把闸门关住。
解:0—0处为等压面,该处表压强2///421.291mkN m g p =⨯=ρ,B 点处表压强:2/807.92m kN m g p p B =⨯-=ρ,A 点处表压强:1//10614.191mkN m g p p B A -⨯=⨯-=ρ。
油对AB 闸门的水平分力:kNRb p p A p P BA x xc x 768.112-=+-=⋅-= kNRR gb G Rb p P B z 296.7)4(2/=-=-=πρρ油式中:油G —41圆柱油的重量。
mR y kN F FR R P P P kN PP P D xz zx527.0sin 768.11cos 798.31arctan846.13022===∴=⨯===+=ααα例11:以ABC 半球内的水为隔离体,求ABC 半球面在n —n 方向对隔离体的法向总作用力P n 及切向总作用力 P 。
解:cos =-+n AC P G P α,απρ+πρ=α+=cos 32cos 320R gR gh G P P AC n ;απρ==τsin 32sin 3R ga G P例12:一直立圆管,直径mm 50,下端平顺地与两平行圆盘间的通道相连接,平行圆盘的半径,3.0m R =间距,6.1mm a =已知各过水断面上的流速均匀分布,高度m H 1=处的A 点流速,/3s m u A =不计水头损失,求A、B、C、D各点的压强值。
解:aRV V d p gV p gV gV p z A CCB221222211124,222ππγγγ=+===++例13:已知U 形比压计中,油的重度为,/16.83m kN 分液面高程的示差,200mm h =∆求水管中A 点的流速u 。
g gh p h g gh p B A ∆--=∆--油ρρρρ,得:h g p p B A ∆-=-)(油ρρgp gp gu u BAA B ρρ+=+=02,02,sm h ggp p gu AB A /81.0)(22=∆-=-=ρρρρ油例14:某水泵在运行时的进口(1-1)处的真空表读数为2m 水柱,出水口(2-2)处的压力表读数为25m ,吸水管直径为,4001mm d =压水管直径为,3002mm d =流量为s /180 ,求水泵的扬程(即水经水泵后的水头增加值)。
解:注意:mp m p p V25,221===-γγγgV p z gV p z H 2222222111++=+++γγ得:H=27.2m例15:射流沿水平方向以速度oV 冲击一倾斜放置的光滑平板,流量为0Q ,不计重力和水头损失,求分流后的流量分配。
(提示:对于光滑平板,反力方向与平板表面正交)。
解此题的关键是:①坐标的选取。
②根据伯努利方程得:210V V V ==220001)90sin(V Q V Q QV ρθρρ=--210V V V ==201cos Q Q Q =-∴θ又210Q Q Q +=2)cos 1(;2)cos 1(0102θθ+=-=∴Q Q Q Q例16:水由图中喷嘴流出,管嘴出口sm mm d /12.15,7533==υ,mmx mm x 220,18012==,132=-z z 不计损失。
计算H 值以m 计,2p 及1p 值以2/m kN 计。
解:sm A A /51.82332==υυ,mgH 66.11223==υ,mgH gp 97.621222=--=υρ,22/4.68mkN p = ,)175.0(175.021122+++=⨯++x x g p g gx p ρρρ水银,求出p值。
1例17:某涵洞宽1.2m,求涵洞上混凝土衬砌物所受的水平总推力。
解:对于明渠,列伯努利方程时,计算点选在水面上。
gV gp gV gp aa29.025.12221++=++ρρ221216.0V V A A V ==2.19.09.0(2);2.15.15.1(2222111⨯⨯==⨯⨯==gA p P gA p P C C ρρ)(1221V V Q T P P -=--ρ得:N T 4.506=例18:图示一水平岔管路,已知,8001mm d =,600,50032mm d mm d ==管轴线在同一水平面内,a kp p 851=,s m V s m Q /5.1,/8.0231==,不计损失。