水力学例题 (1)
- 格式:doc
- 大小:342.00 KB
- 文档页数:19
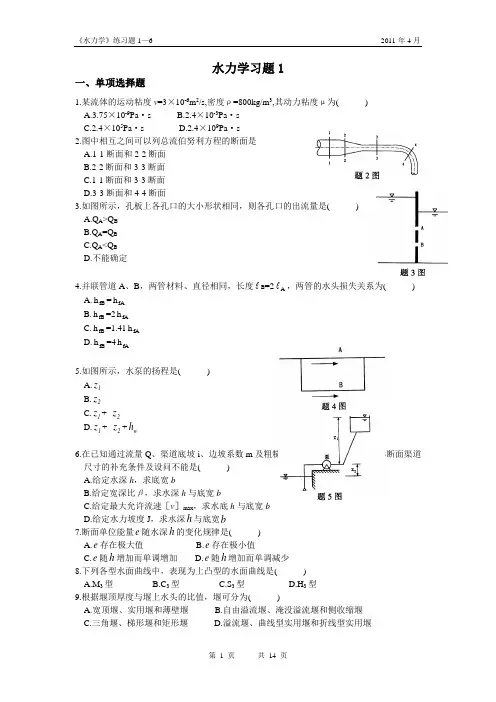
水力学习题1一、单项选择题1.某流体的运动粘度v=3×10-6m2/s,密度ρ=800kg/m3,其动力粘度μ为( )A.3.75×10-9Pa·sB.2.4×10-3Pa·sC.2.4×105Pa·sD.2.4×109Pa·s2.图中相互之间可以列总流伯努利方程的断面是A.1-1断面和2-2断面B.2-2断面和3-3断面C.1-1断面和3-3断面D.3-3断面和4-4断面3.如图所示,孔板上各孔口的大小形状相同,则各孔口的出流量是( )A.Q A>Q BB.Q A=Q BC.Q A<Q BD.不能确定4.并联管道A、B,两管材料、直径相同,长度 B=2 A,两管的水头损失关系为( )A.hfB =hfAB.hfB =2hfAC.hfB =1.41hfAD.hfB =4hfA5.如图所示,水泵的扬程是( )A.z1B.z2C.z1+ z2D.z1+ z2+h w6.在已知通过流量Q、渠道底坡i、边坡系数m及粗糙系数n的条件下,计算梯形断面渠道尺寸的补充条件及设问不能是( )A.给定水深h,求底宽bB.给定宽深比β,求水深h与底宽bC.给定最大允许流速[v]max,求水底h与底宽bD.给定水力坡度J,求水深h与底宽b7.断面单位能量e随水深h的变化规律是( )A.e存在极大值B.e存在极小值C.e随h增加而单调增加D.e随h增加而单调减少8.下列各型水面曲线中,表现为上凸型的水面曲线是( )A.M3型B.C3型C.S3型D.H3型9.根据堰顶厚度与堰上水头的比值,堰可分为( )A.宽顶堰、实用堰和薄壁堰B.自由溢流堰、淹没溢流堰和侧收缩堰C.三角堰、梯形堰和矩形堰D.溢流堰、曲线型实用堰和折线型实用堰10.速度v、长度l、运动粘度v的无量纲组合是( )A.vlv2B.v lv2C.v lv22D.vlv二、填空题(不写解答过程,将正确的答案写在每小题的空格内。

水力学模拟试题及答案1、选择题:(每小题2分)(1)在水力学中,单位质量力是指()a、单位面积液体受到的质量力;b、单位体积液体受到的质量力;c、单位质量液体受到的质量力;d、单位重量液体受到的质量力。
答案:c(2)在平衡液体中,质量力与等压面()a、重合;b、平行c、相交;d、正交。
答案:d(3)液体中某点的绝对压强为100kN/m2,则该点的相对压强为a、1 kN/m2b、2 kN/m2c、5 kN/m2d、10 kN/m2答案:b(4)水力学中的一维流动是指()a、恒定流动;b、均匀流动;c、层流运动;d、运动要素只与一个坐标有关的流动。
答案:d(5)有压管道的管径d与管流水力半径的比值d /R=()a、8;b、4;c、2;d、1。
答案:b(6)已知液体流动的沿程水力摩擦系数 与边壁相对粗糙度和雷诺数Re都有关,即可以判断该液体流动属于a、层流区;b、紊流光滑区;c、紊流过渡粗糙区;d、紊流粗糙区答案:c(7)突然完全关闭管道末端的阀门,产生直接水击。
已知水击波速c=1000m/s,水击压强水头H = 250m,则管道中原来的流速v0为a、1.54m b 、2.0m c 、2.45m d、3.22m答案:c(8)在明渠中不可以发生的流动是()a、恒定均匀流;b、恒定非均匀流;c、非恒定均匀流;d、非恒定非均匀流。
答案:c(9)在缓坡明渠中不可以发生的流动是()。
a、均匀缓流;b、均匀急流;c、非均匀缓流;d、非均匀急流。
答案:b(10)底宽b=1.5m的矩形明渠,通过的流量Q =1.5m3/s,已知渠中某处水深h = 0.4m,则该处水流的流态为a、缓流;b、急流;c、临界流;答案:b(11)闸孔出流的流量Q与闸前水头的H()成正比。
a、1次方b、2次方c、3/2次方d、1/2次方答案:d(12)渗流研究的对象是()的运动规律。
a、重力水;b、毛细水;c、气态水;d、薄膜水。
答案:a(13)测量水槽中某点水流流速的仪器有a、文丘里计b、毕托管c、测压管d、薄壁堰答案:b(14)按重力相似准则设计的水力学模型,长度比尺λL=100,模型中水深为0.1米,则原型中对应点水深为和流量比尺为a、1米,λQ =1000;b、10米,λQ =100;c、1米,λQ =100000;d、10米,λQ=100000。

水力学考试题及答案解析一、单项选择题(每题2分,共20分)1. 水力学中,流体的连续性方程描述的是()。
A. 质量守恒B. 动量守恒C. 能量守恒D. 动量和能量守恒答案:A解析:连续性方程是流体力学中描述质量守恒的基本方程,它表明在没有质量源或汇的情况下,流体的流量在流经任何截面时都是恒定的。
2. 伯努利方程适用于()。
A. 可压缩流体B. 不可压缩流体C. 静止流体D. 任何流体答案:B解析:伯努利方程适用于不可压缩流体,即流体的密度在流动过程中保持不变。
3. 在流体流动中,雷诺数(Re)是描述流体流动状态的重要参数,它与()无关。
A. 流体的密度B. 流体的粘度C. 流动的速度D. 管道的直径答案:B解析:雷诺数是流体流动状态的无量纲数,它与流体的密度、流动的速度和管道的直径有关,但与流体的粘度无关。
4. 流体在管道中流动时,若管道直径增大,则流速()。
A. 增大B. 减小C. 不变D. 无法确定答案:D解析:根据连续性方程,流体的流速与管道的横截面积成反比。
若管道直径增大,而流量保持不变,则流速会减小;若流量增加,则流速可能增大或减小,具体取决于流量的增加程度。
5. 流体的粘性是由于()。
A. 流体分子间的吸引力B. 流体分子间的排斥力C. 流体分子的热运动D. 流体分子的无规则运动答案:A解析:流体的粘性是由于流体分子间的吸引力,这种吸引力使得流体在流动时产生内部摩擦力。
6. 流体的表面张力是由于()。
A. 流体分子间的吸引力B. 流体分子间的排斥力C. 流体分子的热运动D. 流体分子的无规则运动答案:A解析:流体的表面张力是由于流体分子间的吸引力,这种吸引力使得流体的表面具有收缩的趋势。
7. 在流体流动中,若流速增加,则流体的动能()。
A. 增大B. 减小C. 不变D. 无法确定答案:A解析:流体的动能与流速的平方成正比,因此流速增加时,流体的动能也会增加。
8. 流体的压强能是由于()。

水力学简单题库及答案1. 什么是水力学?水力学是研究液体运动规律的科学,主要研究液体在静止和流动状态下的行为。
2. 水力学中的连续性方程是什么?连续性方程是描述液体质量守恒的方程,表达式为:\[ Q_1 = Q_2 \] 其中 \( Q \) 表示流量,即单位时间内流过某一截面的液体体积。
3. 伯努利方程是什么?伯努利方程是描述理想流体在流动过程中能量守恒的方程,表达式为:\[ P + \frac{1}{2}\rho v^2 + \rho gh = \text{常数} \] 其中 \( P \) 是压力,\( \rho \) 是流体密度,\( v \) 是流速,\( g \) 是重力加速度,\( h \) 是高度。
4. 水头损失有哪些类型?水头损失主要有三种类型:局部损失、沿程损失和入口损失。
5. 什么是雷诺数?雷诺数是一个无量纲数,用于描述流体流动的特性,表达式为:\[ Re = \frac{\rho v L}{\mu} \] 其中 \( \rho \) 是流体密度,\( v \) 是流速,\( L \) 是特征长度,\( \mu \) 是流体的动态粘度。
6. 什么是管道的流量系数?管道的流量系数是一个无量纲系数,用于描述管道在给定的压差下流量的能力,表达式为:\[ C_v = \frac{Q}{\sqrt{\frac{2\Delta P}{\rho}}} \]7. 什么是水力梯度线?水力梯度线是表示管道或渠道中不同位置的水头变化的曲线,通常用于分析管道或渠道的水力特性。
8. 什么是临界流速?临界流速是指流体在管道中流动时,从层流过渡到湍流的临界状态的流速。
9. 什么是水力半径?水力半径是描述管道或渠道截面特性的参数,定义为截面面积与湿周的比值。
10. 什么是水力坡度?水力坡度是表示管道或渠道中水流能量变化的参数,定义为单位长度的水头损失。
11. 如何计算管道的沿程损失?管道的沿程损失可以通过达西-韦斯巴赫公式计算:\[ h_f =\frac{f L Q^2}{2.5 g A^2} \] 其中 \( h_f \) 是沿程水头损失,\( f \) 是摩擦系数,\( L \) 是管道长度,\( Q \) 是流量,\( g \) 是重力加速度,\( A \) 是管道横截面积。

1. 下列物理量中,有量纲的数为( )a) A .佛汝德数Fr B. 沿程阻力系数λ b) C .渗流系数k D. 堰流流量系数m 2. 缓坡明渠中的均匀流是( )a) A .缓流 B. 急流 C. 临界流 D. 可以是急流或缓流 3. 管流的负压区是指测压管水头线( )A 在基准面以下的部分 B. 在下游自由水面以下的部分 C . 在管轴线以下的部分 D. 在基准面以上的部分4. 有两条梯形断面渠道1和2,已知其流量、边坡系数、糙率和底坡相同,但底坡i 1>i 2,则其均匀流水深h 1和h 2的关系为( )A .h 1>h 2 B. h 1<h 2 C. h 1=h 2 D. 无法确定 5. 对于并联长管道,每根管道的( )相等。
A .流量 B. 切应力 C. 沿程水头损失 D. 水力坡度 6. 平衡液体的等压面必为( )A .水平面 B. 斜平面 C. 旋转抛物面 D. 与质量力正交的面 7. 理想液体恒定有势流动,当质量力只有重力时, ( )A 整个流场内各点的总水头)2//(2g u p z ++γ相等B 只有位于同一流线上的点,总水头)2//(2g u p z ++γ相等C 沿流线总水头)2//(2g u p z ++γ沿程减小D 沿流线总水头)2//(2g u p z ++γ沿程增加8. 有一溢流堰,堰顶厚度为2m ,堰上水头为2m ,则该堰流属于( )A .薄壁堰流 B. 宽顶堰流 C. 实用堰流 D. 明渠水流 9. 同一管道中,当流速不变,温度上升时,则雷诺数( )A .增大 B. 减小 C. 不变 D. 不一定10. 一段直径不变管道的流速从2m/s 增加到4m/s 时,在水流都处于紊流粗糙区时,沿程水损失是原来的( )倍A .1 B.2 C. 2 D. 41.有一明渠均匀流,通过流量s m Q /553=,底坡0004.0=i ,则其流量模数K = . 2.水泵进口真空计的读数为2/5.24m KN p k =,则该处的相对压强水头为 m3.矩形断面渠道,水深h=1m ,单宽流量s m q /13=,则该水流的佛汝德数Fr = 。
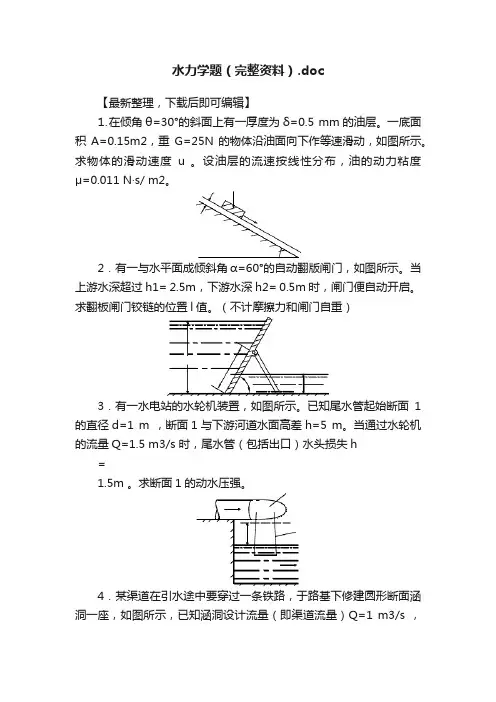
水力学题(完整资料).doc【最新整理,下载后即可编辑】⒈在倾角θ=30°的斜面上有一厚度为δ=0.5 mm的油层。
一底面积A=0.15m2,重G=25N的物体沿油面向下作等速滑动,如图所示。
求物体的滑动速度u 。
设油层的流速按线性分布,油的动力粘度μ=0.011 N·s/ m2。
2.有一与水平面成倾斜角α=60°的自动翻版闸门,如图所示。
当上游水深超过h1= 2.5m,下游水深h2= 0.5m时,闸门便自动开启。
求翻板闸门铰链的位置l值。
(不计摩擦力和闸门自重)3.有一水电站的水轮机装置,如图所示。
已知尾水管起始断面1的直径d=1 m ,断面1与下游河道水面高差h=5 m。
当通过水轮机的流量Q=1.5 m3/s 时,尾水管(包括出口)水头损失h=1.5m 。
求断面1的动水压强。
4.某渠道在引水途中要穿过一条铁路,于路基下修建圆形断面涵洞一座,如图所示,已知涵洞设计流量(即渠道流量)Q=1 m3/s ,涵洞上下游允许水位差z =0.3 m ,涵洞水头损失1h ω =1.4722v g (v 为洞内流速)。
涵洞上下游渠道流速极小。
求涵洞直径d 。
5.图示一从水库引水灌溉的虹吸管,管径d=10 cm ,管中心线的最高点B 高出水库水面2 m 。
管段AB (包括进口)的水头损失AB h ω=3.522v g ,管段BC 的水头损失BC h ω=1.522v g (v 为管中流速)。
若限制管道最大真空高度不超过6 m 水柱,问:(1)虹吸管引水流量量有无限制?如有,最大值为多少?(2)水库水面至虹吸管出口的高差h 有无限制?如有,最大值为多少?B6.有一大水箱,水箱面积很大,下接一管道,如图所示。
已知大管和收缩段管径分别为d 1=5 cm 和d 2=4 cm ,水箱水面与管道出口中心点的高度差H =1 m 。
如不计水头损失,问容器A 中的水是否会沿管B 上升?如上升,上升高度h 为若干?7.有一从水箱引水的管道如图所示。

第1章 绪论例1:已知油品的相对密度为0.85,求其重度。
解:3/980085.085.0m N ⨯=⇒=γδ例2:当压强增加5×104Pa 时,某种液体的密度增长0.02%,求该液体的弹性系数。
解:0=+=⇒=dV Vd dM V M ρρρρρd dV V -= Padp d dp V dV E p 84105.2105%02.01111⨯=⨯⨯==-==ρρβ例3:已知:A =1200cm 2,V =0.5m/sμ1=0.142Pa.s ,h 1=1.0mm μ2=0.235Pa.s ,h 2=1.4mm 求:平板上所受的内摩擦力F绘制:平板间流体的流速分布图及应力分布图 解:(前提条件:牛顿流体、层流运动)dy du μτ= ⎪⎪⎩⎪⎪⎨⎧-=-=⇒2221110h u h u V μτμτ 因为 τ1=τ2 所以sm h h Vh u h uh u V /23.02112212211=+=⇒=-μμμμμN h uV A F 6.411=-==μτ第2章 水静力学例1:如图,汽车上有一长方形水箱,高H =1.2m ,长L =4m ,水箱顶盖中心有一供加水用的通大气压孔,试计算当汽车以加速度为3m/s 2向前行驶时,水箱底面上前后两点A 、B 的静压强(装满水)。
解:分析:水箱处于顶盖封闭状态,当加速时,液面不变化,但由于惯性力而引起的液体内部压力分布规律不变,等压面仍为一倾斜平面,符合0=+s gz ax 等压面与x 轴方向之间的夹角g a tg =θPaL tg H h p A A 177552=⎪⎭⎫ ⎝⎛⋅+==θγγ PaL tg H h p B B 57602=⎪⎭⎫ ⎝⎛⋅-==θγγ例2:(1)装满液体容器在顶盖中心处开口的相对平衡分析:容器内液体虽然借离心惯性力向外甩,但由于受容器顶限制,液面并不能形成旋转抛物面,但内部压强分布规律不变:Cz gr p +-⋅=)2(22ωγ利用边界条件:r =0,z =0时,p =0作用于顶盖上的压强:g r p 222ωγ=(表压)(2)装满液体容器在顶盖边缘处开口的相对平衡压强分布规律:Cz gr p +-⋅=)2(22ωγ边缘A 、B 处:r =R ,z =0,p =0g R C 222ωγ-=作用于顶盖上的压强:()2222r R gp --=ωγ例3:已知:r 1,r 2,Δh求:ω0 解:212120=-s z gr ω (1)222220=-s z gr ω (2)因为 h z z s s ∆==21所以212202r r h g -∆=ω例4已知:一圆柱形容器,直径D =1.2m ,完全充满水,顶盖上在r 0=0.43m 处开一小孔,敞开测压管中的水位a =0.5m ,问此容器绕其立轴旋转的转速n 多大时,顶盖所受的静水总压力为零?已知:D =1.2m ,r 0=0.43m ,a =0.5m 求:n解:据公式 )(Z d z Y d y X d x dp ++=ρ 坐标如图,则 x X 2ω=,y Y 2ω=,g Z -= 代入上式积分:C z gr p +-⋅=)2(22ωγ (*)由题意条件,在A 点处:r =r 0,z =0,p =γa 则 C gr a +-⋅=)02(202ωγγ 所以 )2(202gr a C ωγ-⋅=所以 )2()2(20222gr a z gr p ωγωγ-⋅+-⋅= 当z =0时: )2(220222gr a gr p ωγωγ-⋅+=它是一旋转抛物方程:盖板上静压强沿径向按半径的二次方增长。
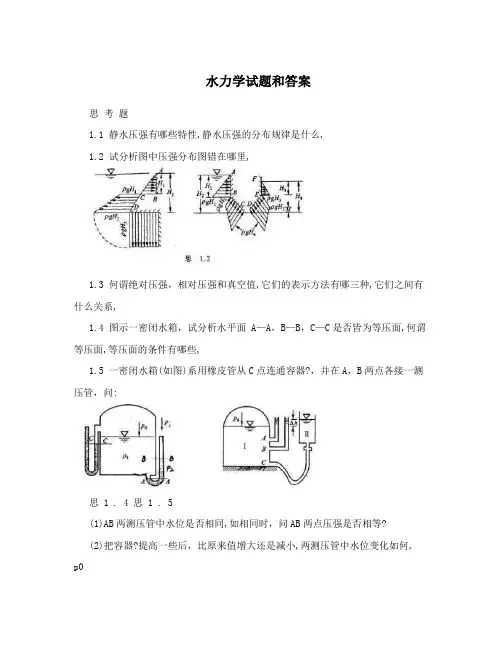
水力学试题和答案思考题1.1 静水压强有哪些特性,静水压强的分布规律是什么,1.2 试分析图中压强分布图错在哪里,1.3 何谓绝对压强,相对压强和真空值,它们的表示方法有哪三种,它们之间有什么关系,1.4 图示一密闭水箱,试分析水平面 A—A,B—B,C—C是否皆为等压面,何谓等压面,等压面的条件有哪些,1.5 一密闭水箱(如图)系用橡皮管从C点连通容器?,并在A,B两点各接一测压管,问:思 1 . 4 思 1 . 5(1)AB两测压管中水位是否相同,如相同时,问AB两点压强是否相等?(2)把容器?提高一些后,比原来值增大还是减小,两测压管中水位变化如何, p01.6 什么叫压力体,如何确定压力体的范围和方向,习题1.1 图示为一密闭容器,两侧各装一测压管,右管上端封闭,其中水面高出容器水3 m,管内液面压强为78 kPa;左管与大气相通。
求: p0(1)容器内液面压强; pch(2)左侧管内水面距容器液面高度。
31.2 盛有同种介质(密度1 132.6 kg/m)的两容器,其中心点A 与B位于同,,,,AB3一高程,今用U形差压计测定A 与B 点之压差(差压计内盛油,密度867.3 kg/m ), A,,0点还装有一水银测压计。
其他有关数据如图题1.2所示。
问:1)A 与B 两点之压差为多少, ((2)A 与B 两点中有无真空存在,其值为多少,31.3 图示一圆柱形油桶,内装轻油及重油。
轻油密度为6 632.6 kg / m,重油密度,,213为887.75k g/m,当两种油重量相等时,求:(1)两种油的深度及为多少, hh12(2)两测压管内油面将上升至什么高度,1.4 在盛满水的容器盖上,加上6 154N 的荷载G(包括盖重),若盖与容器侧壁完密合,试求A ,B ,C ,D 各点的相对静水压强(尺寸见图)。
1.5 今采用三组串联的U形水银测压计测量高压水管中压强,测压计顶端盛水。
当M点压强等于大气压强时,各支水银面均位于0一0水平面上。

例题1在旋转锥阀与阀座之间有厚度为1δ,动力粘度为μ的一层油膜,锥阀高为h,上、下底半径分别为1r 和2r 。
试证明,锥阀以角速度ω旋转时,作用在锥阀上的阻力矩为:2222121212()()()r r r r r r h T πμω++-+=〔解〕证明:任取r 到r+dr 的一条微元锥面环带,在半径r 处的速度梯度是δωγ,切应力ωγτμδ=,假定锥面上的微元环形面积为dA ,则作用在锥阀微元环带表面上的微元摩擦力是dF=τdA微元摩擦力矩 dT=τdA ⨯r下面讨论dA 的表达式,设半锥角为θ,显然,由锥阀的几何关系可得 222121)(hr r r r Sin +--=θθππθSin rdr dA rdr dASin 22== ∴ dr r Sin rdA dT 32θδπμωτ== ()1122441232sin 2sin r r rrr r T dT r dr πμωπμωδθδθ-===⎰⎰ 将)(4241r r -进行因式分解,并将Sin θ的表达式代入化简整理上式可得 2222121212()()()2T r r r r r r h πμωδ=++-+ 例题2盛有水的密闭容器,其底部圆孔用金属圆球封闭,该球重,直径D=10cm ,圆孔直径d=8cm ,水深H 1=50cm 外部容器水面低10cm ,H 2=40cm ,水面为大气压,容器内水面压强为p 0求:(1)当p 0也为大气压时,求球体所受的压力; (2)当p 0为多大的真空度时,球体将浮起。
解:(1)计算p 0=p a 时,球体所受的水压力因球体对称,侧向水压力相互抵消,作用在球体上仅有垂直压力。
如解例题2(a)图,由压力体的概念球体所受水压力为()()⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡--=464622132213d H H D d H H D P γπγππ ())(205.0408.04.05.061.014.3980023↑=⎥⎦⎤⎢⎣⎡⨯--⨯⨯=N(2)计算密闭容器内的真空度 设所求真空度为Hm(水柱)高,欲使球体浮起,必须满足由于真空吸起的“吸力”+上举力=球重,如解例题2(b)图所示,即有平衡式6.19205.042=+d H πγ()()m d H 39.008.014.398004205.06.194205.06.1922=⨯⨯⨯-=-=γπ γKP ≥ p K ≥9800×=3822N/m2当真空度p K ≥3822N/m 2时,球将浮起。

水力学考试题库及答案一、单项选择题(每题2分,共20分)1. 水力学中,流体的连续性方程描述的是()。
A. 质量守恒B. 能量守恒C. 动量守恒D. 角动量守恒答案:A2. 在稳定流动中,流体的总能量沿流线是()。
A. 增加B. 减少C. 保持不变D. 先增加后减少答案:C3. 流体的粘性是由()引起的。
A. 流体的压缩性B. 分子间的吸引力C. 流体的惯性D. 流体的可压缩性答案:B4. 流体的雷诺数(Re)是描述流体流动状态的无量纲数,它与()有关。
A. 流体的密度、速度和管道直径B. 流体的密度、压力和管道直径C. 流体的密度、速度和管道长度D. 流体的密度、压力和管道长度答案:A5. 根据达西-韦斯巴赫方程,流体在管道中流动时的压力降与()成正比。
A. 流速的平方B. 流速的立方C. 流速的四次方D. 流速的五次方答案:A6. 在流体力学中,伯努利方程适用于()。
A. 非稳定流动B. 非均匀流动C. 稳定流动D. 非稳定流动和非均匀流动答案:C7. 流体的比容是指单位质量流体所占的()。
A. 体积B. 质量C. 密度D. 压力答案:A8. 流体的压缩性是指流体在压力作用下体积()的性质。
A. 增加B. 减少C. 不变D. 先增加后减少答案:B9. 流体的表面张力是由于()引起的。
A. 分子间的吸引力B. 分子间的排斥力C. 分子间的重力D. 分子间的电磁力答案:A10. 流体的粘性系数(μ)是描述流体粘性的物理量,它与()有关。
A. 流体的温度和压力B. 流体的温度和密度C. 流体的温度和速度D. 流体的压力和速度答案:A二、多项选择题(每题3分,共15分)11. 水力学中,流体的流动状态可以分为()。
B. 紊流C. 稳定流动D. 非稳定流动答案:A, B, C, D12. 流体的粘性引起的效应包括()。
A. 粘性应力B. 粘性阻力C. 粘性扩散D. 粘性压缩答案:A, B, C13. 流体的雷诺数(Re)可以用来判断流体流动的状态,当Re 值()时,流动为层流。
水力学一、单项选择题1. 图示圆管所受到的单位长度上静水总压力垂直分力的大小是: ()A.17.3kNB.34.7kNC.52kND.69.4kN2. 在静止液体中,静水压强的方向总是()A、倾斜指向受压面B、平行于受压面C、垂直指向受压面D、背离受压面3. 图示垂直置于水中的矩形平板闸门,宽度b=1m,闸门高h=3m,闸门两侧水深分别为,,总压力作用点距闸门底部的铅直距离为: ()A.2.5mB.1.5mC.2mD.1m4. 粘性流体测压管水头线的沿程变化是()A.沿程上升B.沿程下降C.保持水平D.以上情况均有可能5. 测量水槽中某点水流流速的仪器有()A、文丘里计B、毕托管C、测压管D、薄壁堰6. 恒定流具有下列哪种性质()。
A.当地加速度∂u/∂t=0B.迁移加速度∂u/ ∂S=0C.当地加速度∂u/∂t≠0D.迁移加速度∂u/ ∂S≠07. 沿程水头损失与断面平均流速的一次方成正比的水流属()A.层流区B.紊流水力光滑区C.紊流过渡区D.紊流水力粗糙区8. 某一圆形有压油管的直径为d=150mm,流速为v=0.256m/s,长1km,雷诺数1921,其沿程损失为()A.74.25cm油柱B.74.25cm水柱C. 95.26cm油柱D. 62.26cm油柱9. 圆管层流的流速是如何分布的()A.直线分布 B.抛物线分布C.对数曲线分布D.双曲线分布10. 长管并联管道,若管长管径,粗糙度均布相等,但其下述哪个因素相等?()A 水头损失相等B 通过流量相等C 总的能量损失相等D 水力坡度相等11. 串联长管如图所示,通过流量为Q=50L/s,管道阻抗分别为,则水头H为()A 15.64mB 13.53mC 12.72m D14.71m12. 突然放大管道尺寸同上题,若已知放大前断面平均流速为4m/s,则局部水头损失为()A 0.256mB 0.347mC 0.612mD 0.459m13. 明渠水力最佳矩形断面的宽深比是:()A.0.5B.1.0C.3D.214. 具有任意断面形状的均匀流的沿程水头损失有以下哪些特性?()与流程长度成正比,与壁面平均切应力、水力半径成反比与壁面平均切应力成正比,与流路长度、水力半径成反比与流路长度,水力半径成正比,与壁面平均切应力成反比与流路长度、平均切应力成正比,与水力半径成反比15. 有压管道的管径d与管流水力半径的比值d /R=()A.8;B.4;C.2;D.1。
1-1 已知某水流流速分布为10/172.0y u =,u 的单位为m/s ,y 为距壁面的距离,单位为m 。
(1)求y=0.1、0.5、1.0m 处的流速梯度;(2)若水的运动粘滞系数s cm /1010.02=ν,计算相应的切应力。
解:(1)依题知①当y=0.1时,s y dy du19.01.0572.0)1.0(072.0--=≈⨯= ②当y=0.5时,19.05.0134.0)5.0(0072.0--=≈⨯=s dy duy ③当y=1.0时,19.01.0072.0)0.1(072.0--==⨯=s dy duy(2)依题知①当y=0.1时,Pa 41078.5572.000101.0-⨯≈⨯=τ②当y=0.5时,Pa 41035.1134.000101.0-⨯≈⨯=τ③当y=1.0时,Pa 41027.7072.000101.0-⨯≈⨯=τ1-2 已知温度20℃时水的密度3/2.998m kg =ρ,动力粘滞系数23/10002.1m s N ⋅⨯=-μ,求其运动粘滞系数ν?解:1-3 容器内盛有液体,求下述不同情况时该液体所受单位质量力?(1)容器静止时;(2)容器以等加速度g 垂直向上运动;(3)容器以等加速度g 垂直向下运动。
解:(1)依题知(2)依题知gmgg mmg mg f f f z y x 2,0-=--===(3)依题知gmg 0,0=-===mmg mg f f f z y x1-4 根据牛顿内摩擦定律,推导动力粘滞系数μ和运动粘滞系数ν的量纲。
1-5 两个平行边壁间距为25mm ,中间为粘滞系数为μ=0.7Pa ·s 的油,有一mm 250mm 250⨯的平板,在距一个边壁6mm 的距离处以s /mm 150的速度拖行。
设平板与边壁完全平行,并假设平板两边的流速分布均为线性,求拖行平板的力。
1-6 一底面积为40×45cm 2的矩形平板,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,斜面倾角θ=22.62º,如图所示。
水力学练习题及参考答案一、是非题(正确的划“√”,错误的划“×)1、理想液体就是不考虑粘滞性的实际不存在的理想化的液体。
(√)2、图中矩形面板所受静水总压力的作用点与受压面的形心点O重合。
(×)3、园管中层流的雷诺数必然大于3000。
?×?4、明槽水流的急流和缓流是用Fr判别的,当Fr>1为急流。
(√)5、水流总是从压强大的地方向压强小的地方流动。
(×)6、水流总是从流速大的地方向流速小的地方流动。
(×)6、达西定律适用于所有的渗流。
(×)7、闸孔出流的流量与闸前水头的1/2次方成正比。
(√)8、渐变流过水断面上各点的测压管水头都相同。
(√)9、粘滞性是引起液流运动能量损失的根本原因。
(√)10、直立平板静水总压力的作用点就是平板的形心。
(×)11、层流的沿程水头损失系数仅与雷诺数有关。
?√?12、陡坡上出现均匀流必为急流,缓坡上出现均匀流必为缓流。
(√)13、在作用水头相同的条件下,孔口的流量系数比等直径的管嘴流量系数大。
(×)14、两条明渠的断面形状、尺寸、糙率和通过的流量完全相等,但底坡不同,因此它们的正常水深不等。
(√)15、直立平板静水总压力的作用点与平板的形心不重合。
(√)16、水力粗糙管道是表示管道的边壁比较粗糙。
?×?17、水头损失可以区分为沿程水头损失和局部水头损失。
(√)18、牛顿内摩擦定律适用于所有的液体。
(×)19、静止液体中同一点各方向的静水压强数值相等。
(√)20、明渠过流断面上各点的流速都是相等的。
?×?21、缓坡上可以出现均匀的急流。
(√)22、静止水体中,某点的真空压强为50kPa,则该点相对压强为-50 kPa。
(√)24、满宁公式只能适用于紊流阻力平方区。
(√)25、水深相同的静止水面一定是等压面。
(√)26、恒定流一定是均匀流,层流也一定是均匀流。
典型例题【例1】两个平行固定边壁间距为25mm,中间为粘滞系数为μ=0.7Pa·s的油,有一的平板(该平板厚1mm),在距一个边壁4mm的距离处以的速度拖行。
设平板与边壁完全平行,并假设平板两边都系线性流速分布,求拖行平板的力。
【解】由牛顿内摩擦定律,内摩擦力平板两边的流速分布为线性,则平板两边的速度梯度分别为所以由于平板以匀速拖行,因此拖行平板的力F与内摩擦力相等,即:【例2】下图为一溢流坝上的弧形闸门。
已知:R=10m,闸门宽b=8m,。
求作用在该弧形闸门上的静水总压力的大小和方向。
【解】(1)水平分力铅直投影面如图,,方向向右。
(2)铅直分力压力体如图abcde,A cde=扇形面积ode-三角形面积ocd==4.52m2,方向向上。
(3)总压力(4)作用力的方向合力指向曲面,其作用线与水平方向的夹角【例3】如图溢流坝,上游断面水深h 1=1.5m ,下游断面水深h 2=0.6m ,略去水头损失;求水流对2m 坝宽(垂直纸面)的水平作用力。
注:上、下游河床为平底,河床摩擦力不计,为方便计算取ρ=1000kg/m 3,g=10m/s 2。
【解】以1-1与2-2断面及沿坝面(包括上下游部分河床边界)与水流自由表面所围成的空间作为控制体,并取沿水流方向为x 正向。
(1)求上、下游断面的流速以河床为基准面,对1-1与2-2断面写能量方程式因为 p1 = p2 = p , α,1α=2α=1,于是(a )由连续方程得(b)=1.5m ,代入式(a)和(b)将hν=1.83 m/s ,可求得(2)求1-1断面和2-2断面的动水压力(3)计算过水断面的流量(4)沿x方向写动量方程式令坝面对水体的反作用力在水平方向的分力为R,方向向左。
沿x方向的动量方程为所以坝面对水体的反作用力R的方向与所设的方向相同。
水流对坝面的作用力与R大小相等,方向相反。
第1章 绪论例1:已知油品的相对密度为0.85,求其重度。
解:3/980085.085.0m N ⨯=⇒=γδ例2:当压强增加5×104Pa 时,某种液体的密度增长0.02%,求该液体的弹性系数。
解:0=+=⇒=dV Vd dM V M ρρρρρd dV V -= Padp d dp V dV E p 84105.2105%02.01111⨯=⨯⨯==-==ρρβ例3:已知:A =1200cm 2,V =0.5m/sμ1=0.142Pa.s ,h 1=1.0mm μ2=0.235Pa.s ,h 2=1.4mm 求:平板上所受的内摩擦力F绘制:平板间流体的流速分布图及应力分布图 解:(前提条件:牛顿流体、层流运动)dy du μτ= ⎪⎪⎩⎪⎪⎨⎧-=-=⇒2221110h u h u V μτμτ 因为 τ1=τ2 所以sm h h Vh u h uh u V /23.02112212211=+=⇒=-μμμμμN h uV A F 6.411=-==μτ第2章 水静力学例1:如图,汽车上有一长方形水箱,高H =1.2m ,长L =4m ,水箱顶盖中心有一供加水用的通大气压孔,试计算当汽车以加速度为3m/s 2向前行驶时,水箱底面上前后两点A 、B 的静压强(装满水)。
解:分析:水箱处于顶盖封闭状态,当加速时,液面不变化,但由于惯性力而引起的液体内部压力分布规律不变,等压面仍为一倾斜平面,符合0=+s gz ax 等压面与x 轴方向之间的夹角g a tg =θPaL tg H h p A A 177552=⎪⎭⎫ ⎝⎛⋅+==θγγ PaL tg H h p B B 57602=⎪⎭⎫ ⎝⎛⋅-==θγγ例2:(1)装满液体容器在顶盖中心处开口的相对平衡分析:容器内液体虽然借离心惯性力向外甩,但由于受容器顶限制,液面并不能形成旋转抛物面,但内部压强分布规律不变:Cz gr p +-⋅=)2(22ωγ利用边界条件:r =0,z =0时,p =0作用于顶盖上的压强:g r p 222ωγ=(表压)(2)装满液体容器在顶盖边缘处开口的相对平衡压强分布规律:Cz gr p +-⋅=)2(22ωγ边缘A 、B 处:r =R ,z =0,p =0g R C 222ωγ-=作用于顶盖上的压强:()2222r R gp --=ωγ例3:已知:r 1,r 2,Δh求:ω0 解:212120=-s z gr ω (1)222220=-s z gr ω (2)因为 h z z s s ∆==21所以212202r r h g -∆=ω例4已知:一圆柱形容器,直径D =1.2m ,完全充满水,顶盖上在r 0=0.43m 处开一小孔,敞开测压管中的水位a =0.5m ,问此容器绕其立轴旋转的转速n 多大时,顶盖所受的静水总压力为零?已知:D =1.2m ,r 0=0.43m ,a =0.5m 求:n解:据公式 )(Z d z Y d y X d x dp ++=ρ 坐标如图,则 x X 2ω=,y Y 2ω=,g Z -= 代入上式积分:C z gr p +-⋅=)2(22ωγ (*)由题意条件,在A 点处:r =r 0,z =0,p =γa 则 C gr a +-⋅=)02(202ωγγ 所以 )2(202gr a C ωγ-⋅=所以 )2()2(20222gr a z gr p ωγωγ-⋅+-⋅= 当z =0时: )2(220222gr a gr p ωγωγ-⋅+=它是一旋转抛物方程:盖板上静压强沿径向按半径的二次方增长。
而 02)2(22202220=⋅⎥⎥⎦⎤⎢⎢⎣⎡-⋅+=⋅==⎰⎰⎰r d r g r a g r r d r p p d AP RRAπωγωγπ 所以0)2(2202320=⎥⎥⎦⎤⎢⎢⎣⎡-+⎰dr r g r a g r Rωω 即 02)2(420220242=⎥⎥⎦⎤⎢⎢⎣⎡-+Rr g r a r g ωω则 2202022224042Rr ga ga r R -=⇒=+-ωωω所以 22024212Rr ga n -==ππω代入数据得:n =7.118转/秒例5:闸门宽1.2m ,铰在A 点,压力表G 的读数为-14700Pa ,在右侧箱中装有油,其重度γ0=8.33KN/m 3,问在B 点加多大的水平力才能使闸门AB 平衡? 解:把p 0折算成水柱高:m p h 5.1980014700-=-==γ相当于液面下移1.5m ,如图示虚构液面则左侧:()()N A h P c 7056022.11298001=⨯⨯+⨯==γ压力中心距A 点:3.11-2=1.11m右侧:设在B 点加水平力F 使闸门AB 平衡,对A 点取矩 ∑ M A =0 即 AB F h P h P D D +=2211KNF 87.25233.1992.1911.156.70=⨯-⨯=例6:一示压水箱的横剖面如图所示,压力表的读数为0.14个大气压,圆柱体长 L =1.2m ,半径R =0.6m求:使圆柱体保持如图所示位置所需的各分力(圆柱体重量不计)。
解:水平分力:→N A h P x c x 2.119952.16.07.19800=⨯⨯⨯==γ垂直分力:↑第3章 水动力学基础例1:已知:⎪⎩⎪⎨⎧=+-=+=0z y x u t y u t x u 求:t =0 时,A (-1,1)点流线的方程。
解: t y dy t x dx +-=+积分:ln(x+t)=-ln(-y+t)+C → (x+t) (-y+t)=C` 当t =0时,x =-1,y =1,代入上式得: C`=1 所以,过A (-1,1)点流线的方程为:xy =-1例2、伯努利方程式的应用实例 例2-1 : 一般水力计算问题有一喷水装置如图示。
已知h 1=0.3m ,h 2=1.0m ,h 3=2.5m ,求喷水出口流速,及水流喷射高度h (不计水头损失)。
解:① 以3-3断面为基准面,列1-1、3-3两断面的能量方程:()320320000h h p p h h +=⇒++=+++γγ以2-2断面为基准面,列2-2、4-4两断面的能量方程:()g V h h p 200024120+++=++γ 所以,()()()[]()sm h h h h g h h g p gV /57.63.05.28.9222212321204=-⨯⨯=+-+=+-=γ② mg V h 20.2224==例2-2: 节流式流量计已知:U 形水银压差计连接于直角弯管, d 1=300mm ,d 2=100mm,管中流量Q =100L/s试问:压差计读数Δh 等于多少?(不计水头损失)解:以0-0断面为基准面,列1-1、2-2两断面的能量方程:()2g V 2g V 0222211++∆+=++γγp h z p ()2g V V 212221-+∆+=-h z p p γ又s m A Q V /42.13.014.31.04211=⨯⨯==, s m A Q V /74.121.014.31.04222=⨯⨯==由等压面a -a 得压强关系:h p z p Hg ∆-=-γγ21 则 z h p p Hg γγ+∆=-21所以 ()6.1942.174.1222-+∆+=+∆h z z h Hg γγγmmm h Hg 649649.018.8==-=∆γγγ例2-3: 毕托管原理水从立管下端泄出,立管直径为d =50mm ,射流冲击一水平放置的半径R =150mm 的圆盘,若水层离开盘边的厚度δ=1mm 求:流量Q 及汞比压计的读数Δh 。
水头损失不计。
分析:1-1: p 1(=0), V 1(?), z 1(√)2-2: p 2(=0), V 2(?), z 2(√) 3-3: p 3( ?), V 3(=0), z 3(√)(驻点) 每点都有一个未知数,可对任何两点列方程。
解:以圆盘为基准面,列1-1、2-2两断面的能量方程:2gV 022g V 032221++=++δ ①列1-1、3点的能量方程:02g V 03321++=++γp ②据连续性方程:212241V R V d Q ⋅=⋅=δππ ③③代入①式:2242222/4.766416s m d R g V =⎪⎪⎭⎫⎝⎛-=δ (忽略δ/2)V 2=8.74m/s, V 1=4.196m/sV 1代入②式: mp 898.32g V 3213=+=γ所以:s L V A V A Q /23.82211=⋅=⋅=h p Hg ∆=⋅+γγ5.13mmm p h Hg 396396.098006.1398005.19800898.35.13==⨯⨯+⨯=⋅+=∆γγ例2-4: 流动吸力图示为一抽水装置,利用喷射水流在吼道断面上造成的负压,可将M 容器中的积水抽出。
已知:H 、b 、h (不计损失),求:吼道有效断面面积A 1与喷嘴出口断面面积A 2之间应满足什么样的条件能使抽水装置开始工作?解:以1-1为基准面,列0-0、1-1断面的能量方程:2g V 211+=γp h以0`-0`为基准面,列1-1、2-2断面的能量方程:()2gV 2g V 22211=++-γp h H要使抽水机工作: bp ≥-γ1则:()gH V b h g V 2,221=+=又因为:2211V AV A ⋅=⋅所以:b h H V V A A +==1221例3:水头线(局部损失不计)例4:已知:Q =0.001m 3/s ,D =0.01mH w 吸=1m ,h w 排=25m 求:H =?p B =?N 泵=? 解:取1-1、2-2断面列伯努利方程:O mH h z z H w 21232)(=+-=取1-1、B 断面列伯努利方程:W QH N Pap s m V VA Q h p B w B6.31332001.09800108.9/74.122gV 7.0042=⨯⨯==⨯-=∴=⇒=+++=γγ泵吸例5:动量方程已知:一个水平放置的90º弯管输送水d 1=150mm ,d 2=75mm p 1=2.06×105Pa ,Q =0.02m 3/s求:水流对弯管的作用力大小和方向(不计水头损失) 分析:1-1: p 1(√), V 1(可求), z 1(√) 2-2: p 2(?), V 2(可求), z 2(√)解:s m d QA Q V /132.142111===πs m d Q A Q V /527.442222===π取1-1、2-2两断面列伯努利方程对选取的控制体列动量方程: x 方向:)0(111V Q R A p x -=-ρ y 方向:)0(222-=-V Q A p R y ρ 所以,N R NR y x 9583663==NR R R y x 378622=+=66.14==xy R R arctgθ所以,水流对弯管壁的作用力为F 的反作用力F`,大小相等,方向相反。