2013年中考数学压轴题专项练习

2013年中考数学冲刺必备压轴题汇编安徽10.在一张直角三角形纸片的两直角边上各取一点，分别沿斜边中点与这两点的连线剪去两个三角形，剩下的部分是如图所示的直角梯形，其中三边长分别为2、4、3，则原直角三角形纸片的斜边长是（ ）A .10B .54C . 10或54D .10或172解析：考虑两种情况．要分清从斜边中点向哪个边沿着垂线段过去裁剪的.解答：解：如下图，54)44()22(22=++⨯，1054)44()32(22=++⨯14.如图，P 是矩形ABCD 内的任意一点，连接PA 、PB 、PC 、PD ，得到△PAB 、△PBC 、△PCD 、△PDA ，设它们的面积分别是S 1、S 2、S 3、S 4，给出如下结论： ①S 1+S 2=S 3+S 4 ② S 2+S 4= S 1+ S 3 ③若S 3=2 S 1，则S 4=2 S 2 ④若S 1= S 2，则P 点在矩形的对角线上其中正确的结论的序号是_____________解析：过点P 分别向AD 、BC 作垂线段，两个三角形的面积之和42S S +等于矩形面积的一半，同理，过点P 分别向AB 、CD 作垂线段，两个三角形的面积之和31S S +等于矩形面积的一半. 31S S +=42S S +,又因为21S S =，则32S S +=ABCD S S S 2141=+,所以④一定成立 安徽22.如图1，在△ABC 中，D 、E 、F 分别为三边的中点，G 点在边AB 上，△BDG 与四边形ACDG 的周长相等，设BC =a 、AC =b 、AB =c .（1）求线段BG 的长；（2）求证：DG 平分∠EDF ;（3）连接CG ，如图2，若△BDG 与△DFG 相似，求证：BG ⊥CG . 解（1）∵D 、C 、F 分别是△ABC 三边中点 ∴DE ∥21AB ,DF ∥21AC ， 又∵△BDG 与四边形ACDG 周长相等 即BD +DG +BG =AC +CD +DG +AG∴BG =AC +AG ∵BG =AB －AG ∴BG =2AC AB +=2cb +（2）证明：BG =2c b +，FG =BG －BF =2c b +－22bc = ∴FG =DF ,∴∠FDG =∠FGD 又∵DE ∥AB∴∠EDG =∠FGD ∠FDG =∠EDG ∴DG 平分∠EDF （3）在△DFG 中，∠FDG =∠FGD , △DFG 是等腰三角形,∵△BDG 与△DFG 相似,∴△BDG 是等腰三角形,∴∠B =∠BGD ,∴BD =DG , 则CD = BD =DG ,∴B 、CG 、三点共圆, ∴∠BGC =90°,∴BG ⊥CG23.如图，排球运动员站在点O 处练习发球，将球从O 点正上方2m 的A 处发出，把球看成点，其运行的高度y （m ）与运行的水平距离x (m )满足关系式y =a (x －6)2+h .已知球网与O 点的水平距离为9m ，高度为2.43m ，球场的边界距O 点的水平距离为18m 。

1、如图12，已知直线12y x =与双曲线(0)k y k x =>交于A B ，两点，且点A 的横坐标为4． （1）求k 的值；（2）若双曲线(0)ky k x =>上一点C 的纵坐标为8，求A O C △的面积；（3）过原点O 的另一条直线l 交双曲线(0)ky k x =>于P Q ，两点（P 点在第一象限），若由点A B P Q ，，，为顶点组成的四边形面积为24，求点P 的坐标．解：(1)∵点A 横坐标为4 , ∴当 x = 4时，y = 2 .∴ 点A 的坐标为（ 4，2 ）.∵ 点A 是直线 与双曲线 （k>0）的交点 , ∴ k = 4 ×2 = 8 .(2) 解法一：如图12-1，∵ 点C 在双曲线上，y = 8时，x = 1∴ 点C 的坐标为 ( 1, 8 ) .过点A 、C 分别做x 轴、y 轴的垂线，垂足为M 、N ，得矩形DMON .S 矩形ONDM = 32 ， S △ONC = 4 ， S △CDA = 9， S △OAM = 4 .S △AOC = S 矩形ONDM - S △ONC - S △CDA - S △OAM = 32 - 4 - 9 - 4 = 15 .解法二：如图12-2，过点 C 、A 分别做x 轴的垂线，垂足为E 、F ，∵ 点C 在双曲线8y x =上，当y = 8时，x = 1 .∴ 点C 的坐标为 ( 1, 8 ).图12O x A y B x y 21x y 8=∵ 点C 、A 都在双曲线8y x =上 ,∴ S △COE = S △AOF = 4 。

∴ S △COE + S 梯形CEFA = S △COA + S △AOF .∴ S △COA = S 梯形CEFA .∵ S 梯形CEFA = 12×（2+8）×3 = 15 ,∴ S △COA = 15 .（3）∵ 反比例函数图象是关于原点O 的中心对称图形 ,∴ OP=OQ ，OA=OB .∴ 四边形APBQ 是平行四边形 .∴ S △POA = S 平行四边形APBQ = ×24 = 6 .设点P 的横坐标为m （m > 0且4m ≠）,得P ( m , ) .过点P 、A 分别做x 轴的垂线，垂足为E 、F ，∵ 点P 、A 在双曲线上，∴S △POE = S △AOF = 4 .若0＜m ＜4，如图12-3，∵ S △POE + S 梯形PEFA = S △POA + S △AOF ,∴ S 梯形PEFA = S △POA = 6 .∴ 18(2)(4)62m m +⋅-=.4141m8解得m = 2，m = - 8(舍去) .∴ P （2，4）.若 m ＞ 4，如图12-4，∵ S △AOF + S 梯形AFEP = S △AOP + S △POE ,∴ S 梯形PEFA = S △POA = 6 .∴18(2)(4)62m m +⋅-=，解得m = 8，m = - 2 (舍去) .∴ P （8，1）.∴ 点P 的坐标是P （2，4）或P （8，1）.2、如图，抛物线212y x mx n =++交x 轴于A 、B 两点，交y 轴于点C ，点P 是它的顶点，点A的横坐标是-3，点B 的横坐标是1．(1)求m 、n 的值；(2）求直线PC 的解析式；(3）请探究以点A 为圆心、直径为5的圆与直线 PC 的位置关系，并说明理由．(参考数：2 1.41≈，3 1.73≈，5 2.24≈) 解： (1)由已知条件可知： 抛物线212y x mx n =++经过A (-3，0)、B (1，0)两点． ∴ 903,210.2m n m n ⎧=-+⎪⎪⎨⎪=++⎪⎩ ……………………………………2分解得 31,2m n ==-． ………………………3分 (2) ∵21322yx x =+-， ∴ P (-1，-2)，C 3(0,)2-． …………………4分设直线PC 的解析式是y kx b =+，则2,3.2k b b -=-+⎧⎪⎨=-⎪⎩ 解得13,22k b ==-． ∴ 直线PC 的解析式是1322yx =-． …………………………6分 说明：只要求对1322k b ==-，，不写最后一步，不扣分．(3) 如图，过点A 作AE ⊥PC ，垂足为E ．设直线PC 与x 轴交于点D ，则点D 的坐标为(3，0)． ………………………7分 在Rt△O CD 中，∵ O C =32，3O D =， ∴ 2233()3522C D =+=． …………8分∵ O A =3，3O D =，∴AD =6． (9)分 ∵ ∠C O D =∠AED =90o ，∠CD O 公用，∴ △C O D ∽△AED ． ……………10分 ∴ OCC D AEAD =， 即335226AE =． ∴ 655AE =． …………………11分 ∵ 65 2.688 2.55> ，∴ 以点A 为圆心、直径为5的圆与直线PC 相离． …………12分。

1.如图，抛物线的顶点为A （2，1），且经过原点O ，与x 轴的另一个交点为B ．（1）求抛物线的解析式；（2）在抛物线上求点M ，使△MOB 的面积是△AOB 面积的3倍；（3）连结OA ，AB ，在x 轴下方的抛物线上是否存在点N ，使△OBN 与△OAB 相似？若存在，求出N 点的坐标；若不存在，说明理由．解：（1）由题意，可设抛物线的解析式为y ＝a (x －2)2＋1．∵抛物线经过原点，∴a (0－2)2＋1＝0，∴a ＝－41． ∴抛物线的解析式为y ＝－41(x －2)2＋1＝－41x 2＋x ． ························· 3分 （2）△AOB 和所求△MOB 同底不等高，若S △MOB ＝3S △AOB ，则△MOB 的高是△AOB 高的3倍，即M 点的纵坐标是－3． ············································································· 5分∴－41x 2＋x ＝－3，整理得x 2－4x －12＝0，解得x 1＝6，x 2＝－2． ∴满足条件的点有两个：M 1(6，－3)，M 2(－2，－3) ····························· 7分（3）不存在． ········································································································ 8分理由如下：由抛物线的对称性，知AO ＝AB ，∠AOB ＝∠ABO ．若△OBN ∽△OAB ，则∠BON ＝∠BOA ＝∠BNO ．设ON 交抛物线的对称轴于A ′ 点，则A ′ (2，－1)．∴直线ON 的解析式为y ＝－21x ．由21x ＝－41x 2＋x ，得x 1＝0，x 2＝6． ∴N (6，－3)．过点N 作NC ⊥x 轴于C ．在Rt △BCN 中，BC ＝6－4＝2，NC ＝3∴NB ＝2232＋＝13．∵OB ＝4，∴NB ≠OB ，∴∠BON ≠∠BNO ，∴△OBN 与△OAB 不相似． 同理，在对称轴左边的抛物线上也不存在符合条件的N 点．∴在x 轴下方的抛物线上不存在点N ，使△OBN 与△OAB 相似． ····· 10分2.如图，在直角坐标系中，点A 的坐标为(－2，0)，连结OA ，将线段OA 绕原点O 顺时针旋转120°，得到线段OB ．（1）求点B 的坐标；（2）求经过A 、O 、B 三点的抛物线的解析式；（3）在（2）中抛物线的对称轴上是否存在点C ，使△BOC 的周长最小？若存在，求出点C 的坐标；若不存在，请说明理由．（4）如果点P 是（2）中的抛物线上的动点，且在x 轴的下方，那么△PAB 是否有最大面积？若有，求出此时P 点的坐标及△PAB 的最大面积；若没有，请说明理由．（1）如图1，过点B 作BM ⊥x 轴于M ．由旋转性质知OB ＝OA ＝2．∵∠AOB ＝120°，∴∠BOM ＝60°．∴OM ＝OB ·cos60°＝2×21＝1，BM ＝OB ·sin60°＝2×23＝3． ∴点B 的坐标为(1，3)． ··········································· 1分（2）设经过A 、O 、B 三点的抛物线的解析式为y ＝ax 2＋bx ＋c∵抛物线过原点，∴c ＝0． ∴⎪⎩⎪⎨⎧=+=-3024b a b a 解得⎪⎪⎩⎪⎪⎨⎧==33233b a ∴所求抛物线的解析式为y ＝33x 2＋332x ． ······································ 3分 （3）存在． ·········································································································· 4分如图2，连接AB ，交抛物线的对称轴于点C ，连接OC ．∵OB 的长为定值，∴要使△BOC 的周长最小，必须BC ＋OC 的长最小． ∵点A 与点O 关于抛物线的对称轴对称，∴OC ＝AC ．∴BC ＋OC ＝BC ＋AC ＝AB ．由“两点之间，线段最短”的原理可知：此时BC ＋OC 最小，点C 的位置即为所求．设直线AB 的解析式为y ＝kx ＋m ，将A (－2，0)，B (1，3)代入，得⎪⎩⎪⎨⎧=+=+-302m k m k 解得⎪⎪⎩⎪⎪⎨⎧==33233m k∴直线AB 的解析式为y ＝33x ＋332． 抛物线的对称轴为直线x ＝332332⨯-＝－1，即x ＝－1． 将x ＝－1代入直线AB 的解析式，得y ＝33×(－1)＋332＝33． ∴点C 的坐标为(－1，33)． ································································· 6分 （4）△PAB 有最大面积． ·················································································· 7分如图3，过点P 作y 轴的平行线交AB 于点D ．∵S △PAB ＝S △PAD ＋S △PBD＝21(y D －y P )(x B －x A ) ＝21[(33x ＋332)－(33x 2＋332x )](1＋2) ＝－23x 2－23x ＋3 ＝－23(x ＋21)2＋839 ∴当x ＝－21时，△PAB 的面积有最大值，最大值为839．··············· 8分 此时y P ＝33×(－21)2＋332×(－21)＝－43． ∴此时P 点的坐标为(－21，－43)． ···················································· 9分。

2013年中考数学压轴题真题分类汇编：三角形六、三角形 1．（北京）在△ABC 中，BA ＝BC ，∠BAC ＝α，M 是AC 的中点，P 是线段BM 上的动点，将线段P A 绕点P 顺时针旋转2α得到线段PQ ． （1）若α＝60°且点P 与点M 重合（如图1），线段CQ 的延长线交射线BM 于点D ，请补全图形，并写出∠CDB 的度数；（2）在图2中，点P 不与点B ，M 重合，线段CQ 的延长线与射线BM 交于点D ，猜想∠CDB 的大小（用含α的代数式表示），并加以证明；（3）对于适当大小的α，当点P 在线段BM 上运动到某一位置（不与点B ，M 重合）时，能使得线段CQ 的延长线与射线BM 交于点D ，且PQ ＝QD ，请直接写出α的范围．2．（北京模拟）已知，点P 是∠MON 的平分线OT 上的一动点，射线P A 交直线OM 于点A ，将射线P A 绕点P 逆时针旋转交射线ON 于点B ，且使∠APB ＋∠MON ＝180°． （1）求证：P A ＝PB ；（2）若点C 是直线AB 与直线OP 的交点，当S △POB＝3S △PCB时，求PBPC的值； （3）若∠MON ＝60°，OB ＝2，直线P A 交射线ON 于点D ，且满足∠PBD ＝∠ABO ，求OP 的长．3．（北京模拟）已知△ABC 和△DEC 都是等腰直角三角形，C 为它们的公共直角顶点，连接AD 、BE ，F 为线段AD 的中点，连接CF ．（1）如图1，当点D 在BC 边上时，BE 与CF 的数量关系是____________，位置关系是____________，请证明；（2）如图2，把△DEC 绕点C 顺时针旋转α角（0°＜α＜90°），其他条件不变，问（1）中的关系是否仍然成立？若成立，请证明；若不成立，请写出相应的正确的结论并加以证明；图1 A B C Q M (P ) 图2 ABC Q PM M T N O M T N O 备用图 MTNO备用图（3）如图3，把△DEC 绕点C 顺时针旋转45°，BE 、CD 交于点G ．若∠DCF ＝30°，求BGCG及ACDC的值．4．（上海模拟）如图，∠ACB ＝90°，CD 是∠ACB 的平分线，点P 在CD 上，CP ＝2．将三角板的直角顶点放置在点P 处，绕着点P 旋转，三角板的一条直角边与射线CB 交于点E ，另一条直角边与直线CA 、直线CB 分别交于点F 、点G ． （1）当点F 在射线CA 上时 ①求证：PF ＝PE ．②设CF ＝x ，EG ＝y ，求y 与x 的函数解析式并写出函数的定义域． （2）连接EF ，当△CEF 与△EGP 相似时，求EG 的长．5．（上海模拟）已知△ABC 中，AB ＝AC ，BC ＝6，sin B ＝45．点P 从点B 出发沿射线BA 移动，同时点Q 从点C 出发沿线段AC 的延长线移动，点P 、Q 移动的速度相同，PQ 与直线BC 相交于点D ．（1）如图①，当点P 为AB 的中点时，求CD 的长；（2）如图②，过点P 作直线BC 的垂线，垂足为E ，当点P 、Q 在移动的过程中，线段BE 、DE 、CD 中是否存在长度保持不变的线段？请说明理由； （3）如图③，当PQ 经过△ABC 的重心G 时，求BP 的长．6．（上海模拟）如图，三角形纸片ABC 中，∠C ＝90°，AC ＝4，BC ＝3．将纸片折叠，使点B 落在AC 边上的点D 处，折痕与BC 、AB 分别交于点E 、F ．A CB F P D G E AC BP D备用图A D CB P Q 图② E A DC B P Q 图① AD CB PQ图③ G AB C D EF图1 A B C DEF图2 A B C D EF图3 G（1）设BE ＝x ，DC ＝y ，求y 关于x 的函数关系式，并确定自变量x 的取值范围； （2）当△ADF 是直角三角形时，求BE 的长； （3）当△ADF 是等腰三角形时，求BE 的长（4）过C 、D 、E 三点的圆能否与AB 边相切？若能，求BE 的长；若不能，说明理由．7．（上海模拟）如图，在Rt △ABC 中，∠BAC ＝90°，AB ＝6，AC ＝8，AD ⊥BC 于D ，点E 、F 分别是AB 边和AC 边上的动点，且∠EDF ＝90°，连接EF ． （1）求DEDF的值； （2）设AE 的长为x ，△DEF 的面积为S ，求S 关于x 的函数关系式；（3）设直线DF 与直线AB 相交于点G ，△EFG 能否成为等腰三角形？若能，求AE 的长；若不能，请说明理由．8．（上海模拟）如图，在Rt △ABC 中，∠C ＝90°，AC ＝4，BC ＝5，D 是BC 边上一点，CD ＝3，P 是AC 边上一动点（不与A 、C 重合），过点P 作PE ∥BC 交AD 于点E ． （1）设AP ＝x ，DE ＝y ，求y 关于x 的函数关系式；（2）以PE 为半径的⊙E 与以DB 为半径的⊙D 能否相切？若能，求tan ∠DPE 的值；若不能，请说明理由；（3）将△ABD 沿直线AD 翻折，得到△AB ′D ，连接B ′C ，当∠ACE ＝∠BCB ′时，求AP 的长．9．（上海模拟）已知Rt △ABC 中，∠ACB ＝90°，点P 是边AB 上的一个动点，连接CP ，过AB C DE F A B C C B A D EFC B AD 备用图 CB AD 备用图 AD C B 备用图 A D C B P E点B 作BD ⊥CP ，垂足为点D .（1）如图1，当CP 经过△ABC 的重心时，求证：△BCD ∽△ABC ；（2）如图2，若BC ＝2厘米，cot A ＝2，点P 从点A 向点B 运动（不与点A 、B 重合），点P 的速度是5厘米/秒，设点P 运动的时间为t 秒，△BCD 的面积为S 平方厘米，求S 关于t 的函数解析式，并写出自变量t 的取值范围；（3）在（2）的条件下，若△PBC 是以CP 为腰的等腰三角形，求△BCD 的面积．10．（上海模拟）如图，在Rt △ABC 中，∠ACB ＝90°，CE 是斜边AB 上的中线，AB ＝10，tan A ＝43．点P 是CE 延长线上的一动点，过点P 作PQ ⊥CB ，交CB 延长线于点Q ．设EP ＝x ，BQ ＝y ．（1）求y 关于x 的函数关系式及定义域；（2）连接PB ，当PB 平分∠CPQ 时，求∠PE 的长；（3）过点B 作BF ⊥AB 交PQ 于F ，当△BEF 和△QBF 相似时，求x 的值．11．（上海模拟）如图1，在Rt △AOC 中，AO ⊥OC ，点B 在OC 边上，OB ＝6，BC ＝12，∠ABO ＋∠C ＝90°，动点M 和N 分别在线段AB 和AC 边上． （1）求证：△AOB ∽△COA ，并求cos C 的值；（2）当AM ＝4时，△AMN 与△ABC 相似，求△AMN 与△ABC 的面积之比； （3）如图2，当MN ∥BC 时，以MN 所在直线为对称轴将△AMN 作轴对称变换得△EMN ．设MN ＝x ，△EMN 与四边形BCNM 重叠部分的面积为y ，求y 关于x 的函数关系式，并写出自变量x 的取值范围．C A P BD 图1 C A PB D图2 C AB备用图 AB PC Q E A B C E 备用图 AB C E 备用图 A O NC B M 图1 AO N EC B M 图212．（上海模拟）把两块边长为4的等边三角板ABC 和DE 如图1放置，使三角板DEF 的顶点D 与三角板ABC 的AC 边的中点重合，DF 经过点B ，射线DE 与射线AB 相交于点M ．把三角板ABC 固定不动，将三角板DEF 绕点D 按逆时针方向旋转，设旋转角为α，其中0°＜α＜90°，射线DF 与线段BC 相交于点Q （如图2）． （1）当0°＜α＜60°时，求AM ·CN 的值； （2）当0°＜α＜60°时，设AM ＝x ，两块三角板重叠部分的面积为y ，求y 与x 的函数关系式并确定自变量x 的取值范围；（3）当BM ＝2时，求两块三角板重叠部分的面积．13．（上海模拟）如图，在△ABC 中，∠ACB ＝90°，∠A ＝60°，AC ＝2，CD ⊥AB ，垂足为点D ，点E 、F 分别在边AC 、BC 上，且∠EDF ＝60°．设AE ＝x ，BF ＝y ． （1）求y 关于x 的函数关系式，并写出自变量x 的取值范围；（2）△BDF 能否成为等腰三角形？如果能，请求出x 的值，如果不能，请说明理由．14．（上海模拟）如图，P 是线段AB 上任意一点（不与点A 、B 重合），分别以AP 、BP 为边，在AB 的同侧作等边△APD 和等边△BPC ，连接BD 与PC 交于点E ，连接CD ． （1）当BC ⊥CD 时，试求∠DBC 的正切值；（2）若线段CD 是线段DE 和DB 的比例中项，试求此时APPB的值； （3）记四边形ABCD 的面积为S ，当P 在线段AB 上运动时，S 与BD 2是否成正比例？若成正比例，试求出比例系数；若不成正比例，请说明理由．A B C DE F M图1 AB C D E FM 图2 N A B C备用图AFBC DE D AC B PED AC BP E备用图15．（上海模拟）如图，在△ABC中，AB＝AC＝5，BC＝6，D是AC边的中点，E是BC边上一动点（不与端点重合），EF∥BD交AC于F，交AB延长线于G，H是BC延长线上的点，且CH＝BE，连接FH．设BE＝x，CF＝y．（1）求y关于x的函数关系式；（2）连接AE，当以GE为半径的⊙G和以FH为半径的⊙F相切时，求tan∠BAE的值；（3）当△BEG与△FCH相似时，求BE的长．16．（上海模拟）如图，△ABC中，∠ABC＝90°，AB＝BC＝4，点O为AB边的中点，点M 是BC边上一动点（不与点B、C重合），AD⊥AB，垂足为点A．连接MO，将△BOM沿直线MO翻折，点B落在点B1处，直线MB1与AC、AD分别交于点F、N．（1）当∠CMF＝120°时，求BM的长；（2）设BM＝x，y＝△CMF的周长△ANF的周长，求y关于x的函数关系式。

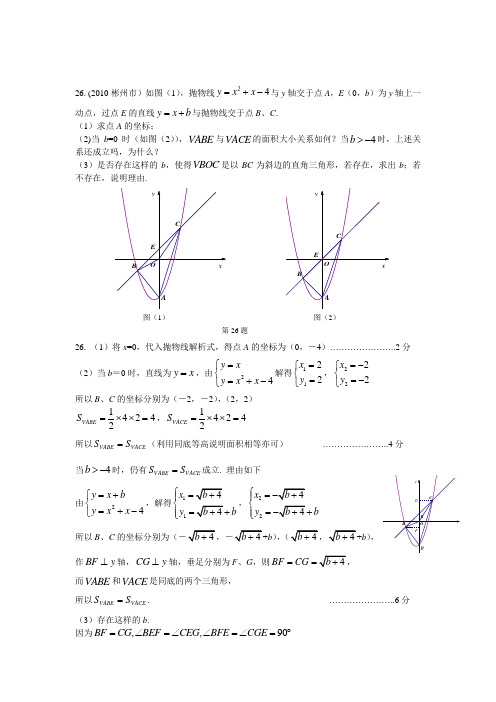
26. (2010彬州市）如图（1），抛物线42y x x =+-与y 轴交于点A ，E （0，b ）为y 轴上一动点，过点E 的直线y x b =+与抛物线交于点B 、C .（1）求点A 的坐标； （2)当b =0时（如图（2）），ABE 与ACE 的面积大小关系如何？当4b >-时，上述关系还成立吗，为什么？（3）是否存在这样的b ，使得BOC 是以BC 为斜边的直角三角形，若存在，求出b ；若不存在，说明理由.26. （1）将x =0，代入抛物线解析式，得点A 的坐标为（0，－4）…………………..2分（2）当b ＝0时，直线为y x =，由24y x y x x =⎧⎨=+-⎩解得1122x y =⎧⎨=⎩，2222x y =-⎧⎨=-⎩ 所以B 、C 的坐标分别为（－2，－2），（2，2）14242ABE S =⨯⨯= ，14242ACE S =⨯⨯=所以ABE ACE S S = （利用同底等高说明面积相等亦可） …………………..4分 当4b >-时，仍有ABE ACE S S = 成立. 理由如下由24y x b y x x =+⎧⎨=+-⎩，解得1144x b y b b ⎧=+⎪⎨=++⎪⎩，2244x b y b b⎧=-+⎪⎨=-++⎪⎩ 所以B 、C 的坐标分别为（－4b +，－4b ++b ），（4b +，4b ++b ）， 作BF y ⊥轴，CG y ⊥轴，垂足分别为F 、G ，则4BF CG b ==+，y xCBAOE y xCBAOE 第26题图（1） 图（2）GFyBCQO R而ABE 和ACE 是同底的两个三角形，所以ABE ACE S S = . …………………..6分 （3）存在这样的b .因为90BF CG,BEF CEG,BFE CGE =∠=∠∠=∠=︒ 所以BEF CEG ≅所以BE CE =，即E 为BC 的中点所以当OE =CE 时，OBC 为直角三角形 …………………..8分 因为44GE b b b b GC =++-=+= 所以 24CE b =⋅+，而OE b = 所以24b b ⋅+=，解得124,2b b ==-，所以当b ＝4或－2时，ΔOBC 为直角三角形. ………………….10分 25.(常德）如图9，已知抛物线212y x bx c x =++与轴交于点A （-4，0）和B （1，0）两点，与y 轴交于C 点. (1)求此抛物线的解析式；(2)设E 是线段AB 上的动点，作EF ∥AC 交BC 于F ，连接CE ，当CEF 的面积是BEF 面积的2倍时，求E 点的坐标；(3)若P 为抛物线上A 、C 两点间的一个动点，过P 作y 轴的平行线，交AC 于Q ，当P 点运动到什么位置时，线段PQ 的值最大，并求此时P 点的坐标.25．解：（1）由二次函数212y x bx c =++与x 轴交于(4,0)A -、(1,0)B 两点可得： 221(4)4021102b c b c ⎧--+=⎪⎪⎨⎪⋅++=⎪⎩，． 解得： 322b c ⎧=⎪⎨⎪=-⎩，．ABOC 图9yx故所求二次函数的解析式为213222y x x =+-． ………………3分 （2）∵S △CEF =2 S △BEF , ∴1,2BF CF =1.3BF BC =………………4分∵EF //AC , ∴B ,EF BAC BFE BCA ∠=∠∠=∠ ,∴△BEF ～△BAC ,………………5分 ∴1,3BE BF BA BC ==得5,3BE = ………………6分 故E 点的坐标为(23-,0).………………7分（3）解法一：由抛物线与y 轴的交点为C ，则C 点的坐标为（0，－2）．若设直线AC的解析式为y kx b =+，则有20,04b k b -=+⎧⎨=-+⎩． 解得：1,22k b ⎧=-⎪⎨⎪=-⎩．故直线AC 的解析式为122y x =-－．………………8分若设P 点的坐标为213,222a a a ⎛⎫+- ⎪⎝⎭，又Q 点是过点P 所作y 轴的平行线与直线AC 的交点，则Q 点的坐标为（1,2)2a a --．则有： 2131[(2)](2)222PQ a a a =-+----＝2122a a --＝()21222a -++即当2a =-时，线段PQ 取大值，此时P 点的坐标为（－2，－3）………10分 解法二：延长PQ 交x 轴于D 点，则PD AB ⊥．要使线段PQ 最长，则只须△APC的面积取大值时即可.………………8分设P 点坐标为（),00y x ，则有:ACO DPCO S APC ADP S S S =+- 梯形 ＝111()222AD PD PD OC OD OA OC ⋅++⋅-⋅ ＝()()000001112242222x y y y x --+-+⋅--⨯⨯＝0024y x ---＝20001322422x x x ⎛⎫-+--- ⎪⎝⎭＝2004xx -- ＝－()22024x ++即02x =-时，△APC 的面积取大值，此时线段PQ 最长，则P 点坐标为（－2，－3）25．（长沙）已知：二次函数22y ax bx =+-的图象经过点（1，0），一次函数图象经过原点和点（1，－b ），其中0a b >>且a 、b 为实数．（1）求一次函数的表达式（用含b 的式子表示）； （2）试说明：这两个函数的图象交于不同的两点；（3）设（2）中的两个交点的横坐标分别为x 1、x 2，求| x 1－x 2 |的范围．25．解：（1）∵一次函数过原点∴设一次函数的解析式为y =kx∵一次函数过（1，－b ） ∴y =－bx ……………………………3分 （2）∵y =ax 2+bx －2过（1，0）即a +b =2 …………………………4分 由2(2)2y bxy b x bx =-⎧⎨=-+-⎩得 ……………………………………5分22(2)20ax a x +--=① ∵△＝224(2)84(1)120a a a -+=-+>∴方程①有两个不相等的实数根∴方程组有两组不同的解∴两函数有两个不同的交点． ………………………………………6分 （3）∵两交点的横坐标x 1、x 2分别是方程①的解 ∴122(2)24a a x x a a--+== 122x x a -= ∴2121212()4x x x x x x -=+-＝22248164(1)3a a a a-+=-+ 或由求根公式得出 ………………………………………………………8分∵a >b >0，a +b =2 ∴2>a >1令函数24(1)3y a=-+ ∵在1<a <2时y 随a 增大而减小．∴244(1)312a<-+< ……………………………………………9分∴242(1)323a<-+< ∴12223x x <-< ………………10分26．(长春）如图①，在平面直角坐标系中，等腰直角△AOB 的斜边OB 在x 轴上，顶点A的坐标为(3，3)，AD 为斜边上的高．抛物线y ＝ax 2＋2x 与直线y ＝ 12x 交于点O 、C ，点C 的横坐标为6．点P 在x 轴的正半轴上，过点P 作PE ∥y 轴，交射线OA 于点E ．设点P 的横坐标为m ，以A 、B 、D 、E 为顶点的四边形的面积为S ． (1)求OA 所在直线的解析式． (2)求a 的值．(3)当m ≠3时，求S 与m 的函数关系式．(4)如图②，设直线PE 交射线OC 于点R ，交抛物线于点Q ．以RQ 为一边，在RQ 的右侧作矩形RQMN ，其中RN ＝ 32．直接写出矩形RQMN 与△AOB 重叠部分为轴对称图形时m 的取值范围．25．（滨州市）（本题满分l0分）如图，四边形ABCD 是菱形，点D 的坐标是（0，3），以点C 为顶点的抛物线c bx ax y ++=2恰好经过x 轴上A 、B 两点．（1）求A 、B 、C 三点的坐标；（2）求过A 、B 、C 三点的抛物线的解析式；（3）若将上述抛物线沿其对称轴向上平移后恰好过D 点，求平移后抛物线的解析式，并指出平移了多少个单位?25．（本题满分l0分）解：①由抛物线的对称性可知AM=BM 在Rt △AOD 和Rt △BMC 中， ∵OD=MC ，AD=BC ， ∴△AOD ≌△BMC ．∴OA=MB=MA ．………………………………………l 分 设菱形的边长为2m ， 在Rt △AOD 中，OOA ABB CCP DEQP DN MR Eyyxx 图①图②222)2()3(m m =+解得m=1．∴DC=2，OA=1，OB=3．∴A 、B 、C 三点的坐标分别为（1，0）、（3，0）、（2，3）………………… 4分 ②设抛物线的解析式为y=a （x —2）2+3 代入A 点坐标可得a =—3抛物线的解析式为y=—3（x —2）2+3……………………………………7分 ③设抛物线的解析式为y =—3（x 一2）2+k 代入D （0，3）可得k=53所以平移后的抛物线的解析式为y =—3（x 一2）2+53…………………………9分 平移了53一3=43个单位．…………………………………………………l0 26. (本溪市）如图，OABC 是一张放在平面直角坐标系中的矩形纸片，O 为原点，点A 在x 轴的正半轴上，点C 在y 轴的正半轴上，53OA OC ==，．（1）在AB 边上取一点D ，将纸片沿OD 翻折，使点A 落在BC 边上的点E 处，求点D ，E 的坐标；（2）若过点D E ，的抛物线与x 轴相交于点(50)F -，，求抛物线的解析式和对称轴方程； （3）若（2）中的抛物线与y 轴交于点H ，在抛物线上是否存在点P ，使PFH △的内心在坐标轴．．．上？若存在，求出点P 的坐标，若不存在，请说明理由． （4）若（2）中的抛物线与y 轴相交于点H ，点Q 在线段OD 上移动，作直线HQ ，当点Q 移动到什么位置时，O D ，两点到直线HQ 的距离之和最大？请直接写出此时点Q 的坐标及直线HQ 的解析式．BCEy3(第26题)28．(甘肃）(12分) 如图，抛物线与x 轴交于A （－1，0）、B （3，0）两点，与y 轴交于点C （0，－3），设抛物线的顶点为D ．（1）求该抛物线的解析式与顶点D 的坐标；（2）以B 、C 、D 为顶点的三角形是直角三角形吗？为什么？（3）探究坐标轴上是否存在点P ，使得以P 、A 、C 为顶点的三角形与△BCD 相似？若存在，请指出符合条件的点P 的位置，并直接写出点P 的坐标；若不存在，请说明理由．28．本小题满分12分解：（1）设该抛物线的解析式为c bx ax y ++=2，由抛物线与y 轴交于点C （0，－3）,可知3-=c .即抛物线的解析式为32-+=bx ax y ． ………………………1分 把A （－1，0）、B （3，0）代入, 得30,9330.a b a b --=⎧⎨+-=⎩解得2,1-==b a .∴ 抛物线的解析式为y = x 2－2x －3． ……………………………………………3分 ∴ 顶点D 的坐标为()4,1-. ……………………………………………………4分说明：只要学生求对2,1-==b a ，不写“抛物线的解析式为y = x 2－2x －3”不扣分. （2）以B 、C 、D 为顶点的三角形是直角三角形. ……………………………5分 理由如下：过点D 分别作x 轴、y 轴的垂线，垂足分别为E 、F.在Rt △BOC 中，OB=3，OC=3，∴ 182=BC . …………………………6分 在Rt △CDF 中，DF=1，CF=OF-OC=4-3=1，∴ 22=CD . …………………………7分 在Rt △BDE 中，DE=4，BE=OB-OE=3-1=2，∴ 202=BD . …………………………8分 ∴ 222BD CD BC =+， 故△BCD 为直角三角形. …………………………9分 （3）连接AC ，可知Rt △COA ∽ Rt △BCD ，得符合条件的点为O （0，0）． ………10分过A 作AP 1⊥AC 交y 轴正半轴于P 1，可知Rt △CAP 1 ∽ Rt △COA ∽ Rt △BCD ，求得符合条件的点为)31,0(1P ． …………………………………………11分 过C 作CP 2⊥AC 交x 轴正半轴于P 2，可知Rt △P 2CA ∽ Rt △COA ∽ Rt △BCD ， 求得符合条件的点为P 2（9，0）． …………………………………………12分∴符合条件的点有三个：O （0，0），)31,0(1P ，P 2（9，0）.。

2013年中考压轴题精选”“XX专题训练一．解答题（共7小题）1．（2010•绵阳）如图，抛物线y=ax2+bx+4与x轴的两个交点分别为A（﹣4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．（1）求抛物线的函数解析式，并写出顶点D的坐标；（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长；（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，△EFK的面积最大？并求出最大面积．2．已知抛物线y=ax2+bx+c的图象如图所示，根据图象解答下列问题：（1）抛物线与x轴的另一个交点坐标；_________；（2）方程ax2+bx+c=0的两个根是_________；（3）不等式ax2+bx+c＜0的解是_________；（4）y随x的增大而减小的自变量x的取值范围是_________；（5）求出抛物线的解析式及顶点坐标．3．（2012•遵义）如图，已知抛物线y=ax2+bx+c（a≠0）的图象经过原点O，交x轴于点A，其顶点B的坐标为（3，﹣）．（1）求抛物线的函数解析式及点A的坐标；（2）在抛物线上求点P，使S△POA=2S△AOB；（3）在抛物线上是否存在点Q，使△AQO与△AOB相似？如果存在，请求出Q点的坐标；如果不存在，请说明理由．4．如图，在平面直角坐标系中，矩形OABC的顶点A（3，0），C（0，1）．将矩形OABC绕原点逆时针旋转90°，得到矩形OA′B′C′．设直线BB′与x轴交于点M、与y轴交于点N，抛物线y=ax2+bx+c的图象经过点C′、M、N．解答下列问题：（1）求出该抛物线所表示的函数解析式；（2）将△MON沿直线BB′翻折，点O落在点P处，请你判断点P是否在该抛物线上，并请说明理由；（3）将该抛物线进行一次平移（沿上下或左右方向），使它恰好经过原点O，求出所有符合要求新抛物线的解析式．5．（2009•柳州）如图，已知抛物线y=ax2﹣2ax﹣b（a＞0）与x轴的一个交点为B（﹣1，0），与y轴的负半轴交于点C，顶点为D．（1）直接写出抛物线的对称轴，及抛物线与x轴的另一个交点A的坐标；（2）以AD为直径的圆经过点C．①求抛物线的解析式；②点E在抛物线的对称轴上，点F在抛物线上，且以B，A，F，E四点为顶点的四边形为平行四边形，求点F的坐标．6．如图，在直角坐标平面内，O为原点，抛物线y=ax2+bx经过点A（6，0），且顶点B（m，6）在直线y=2x上．（1）求m的值和抛物线y=ax2+bx的解析式；（2）如在线段OB上有一点C，满足OC=2CB，在x轴上一点D（10，0），连接DC，且直线DC与y轴交于点E．①求直线DC的解析式；②如点M是直线DC上的一个动点，在x轴上方的平面内有另一点N，且以O、E、M、N为顶点的四边形是菱形，请求出点N的坐标．（直接写出结果，不需要过程．）7．（2008•宜宾）已知：如图，抛物线y=﹣x2+bx+c与x轴、y轴分别相交于点A（﹣1，0）、B（0，3）两点，其顶点为D．（1）求该抛物线的解析式；（2）若该抛物线与x轴的另一个交点为E．求四边形ABDE的面积；（3）△AOB与△BDE是否相似？如果相似，请予以证明；如果不相似，请说明理由．（注：抛物线y=ax2+bx+c（a≠0）的顶点坐标为）如图所示，在平面直角坐标系中，抛物线y=ax2+bx+c经过A（﹣1，0）、B（0，﹣5）、C（5，0）．（1）求此抛物线的表达式；（2）若平行于x轴的直线与此抛物线交于E、F两点，以线段EF为直径的圆与x轴相切，求该圆的半径；（3）在点B、点C之间的抛物线上有点D，使△BDC的面积最大，求此时点D的坐标及△BDC的面积．，解得因为抛物线的对称轴为直线解得：解得所以圆的半径为答：该圆的半径是．）代入得：解得：时，，，﹣，，﹣的面积是．。

2013中考压轴试题代数几何综合1、（2013年潍坊市压轴题）如图，抛物线c bx ax y ++=2关于直线1=x 对称，与坐标轴交于C B A 、、三点，且4=AB ,点⎪⎭⎫ ⎝⎛232，D 在抛物线上，直线是一次函数()02≠-=k kx y 的图象，点O 是坐标原点.（）求抛物线的解析式；（）若直线平分四边形OBDC 的面积，求k 的值.（）把抛物线向左平移1个单位，再向下平移2个单位，所得抛物线与直线交于N M 、两点，问在y 轴正半轴上是否存在一定点P ，使得不论k 取何值，直线PM 与PN 总是关于y 轴对称？若存在，求出P 点坐标；若不存在，请说明理由.答案：（1）因为抛物线关于直线x=1对称，AB=4，所以A(-1，0),B(3，0),由点D(2，1.5)在抛物线上，所以⎩⎨⎧=++=+-5.1240c b a c b a ，所以3a+3b=1.5,即a+b=0.5,又12=-a b ，即b=-2a,代入上式解得a =-0.5,b =1,从而c=1.5,所以23212++-=x x y . （）由（1）知23212++-=x x y ，令x=0,得c(0,1.5),所以CD//AB,令kx -2=1.5,得l 与CD 的交点F(23,27k )，令kx -2=0，得l 与x 轴的交点E(0,2k)，根据S 四边形OEFC =S 四边形EBDF 得：OE+CF=DF+BE,即：,511),272()23(272=-+-=+k k k k k 解得 （3）由（1）知,2)1(21232122+--=++-=x x x y所以把抛物线向左平移1个单位，再向下平移2个单位，所得抛物线的解析式为221x y -=假设在y 轴上存在一点P(0，t)，t ＞0，使直线PM 与PN 关于y 轴对称，过点M 、N 分别向y 轴作垂线MM 1、NN 1，垂足分别为M 1、N 1，因为∠MPO=∠NPO,所以Rt △MPM 1∽Rt △NPN 1, 所以1111PN PM NN MM =,………………(1) 不妨设M(x M ,y M )在点N(x N ,y N )的左侧，因为P 点在y 轴正半轴上， 则（1）式变为NMN M y t y t x x --=-,又y M =k x M -2, y N =k x N -2,把2交（（（D （点A(-1,0)、点B 是二次函数y=ax 2-2 的图象与x 轴的交点，a-2=0,a=2. 二次函数的解析式为y=2x 2-2；②点B 与点A(-1,0)关于直线x=0对称，点B 的坐标为（1，0）； （2）∠BOC=∠PDB=90º，点P 在直线x=m 上，设点P 的坐标为（m,p ）, OB=1， OC=2， DB= m-1 , DP=|p| ，①当△BOC ∽△PDB 时，OB OC = DP DB ,12= |p|m-1 ,p= m-12 或p = 1- m2,点P 的坐标为（m ，m-12 ）或（m ，1- m2 ）；②当△BOC ∽△BDP 时，OB OC = DB DP ，12= m-1|p|，p=2m-2或p=2-2m, 点P 的坐标为（m ，2m-2）或（m ，2-2m ）；综上所述点P 的坐标为（m ，m-12 ）、（m ，1- m2 ）、（m ，2m-2）或（m ，2-2m ）；（3）不存在满足条件的点Q 。

2013年中考数学压轴题精选1. 如图，在平面直角坐标系中，直线112y x =+与抛物线y ＝ax 2＋bx －3交于A 、B 两点，点A 在x 轴上，点B 的纵坐标为3．点P 是直线AB 下方的抛物线上的一动点（不与点A 、B 重合），过点P 作x 轴的垂线交直线AB 于点C ，作PD ⊥AB 于点D ．（1）求a 、b 及sin ∠ACP 的值；（2）设点P 的横坐标为m ．①用含m 的代数式表示线段PD 的长，并求出线段PD 长的最大值；②连结PB ，线段PC 把△PDB 分成两个三角形，是否存在适合的m 的值，使这两个三角形的面积比为 9∶10？若存在，直接写出m 的值；若不存在，请说明理由．2. 如图1，已知抛物线212y x bx c =++（b 、c 是常数，且c ＜0）与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴的负半轴交于点C ，点A 的坐标为(－1,0)．（1）b ＝______，点B 的横坐标为_______（上述结果均用含c 的代数式表示）；（2）连结BC ，过点A 作直线AE //BC ，与抛物线交于点E ．点D 是x 轴上一点，坐标为(2,0)，当C 、D 、E 三点在同一直线上时，求抛物线的解析式；（3）在（2）的条件下，点P 是x 轴下方的抛物线上的一动点，连结PB 、PC ．设△PBC 的面积为S ． ①求S 的取值范围；②若△PBC 的面积S 为正整数，则这样的△PBC 共有_____个．3.如图1，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动，动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动，过点P作PD//BC，交AB于点D，联结PQ．点P、Q分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动的时间为t秒（t≥0）．（1）直接用含t的代数式分别表示：QB＝_______，PD＝_______；（2）是否存在t的值，使四边形PDBQ为菱形？若存在，求出t的值；若不存在，说明理由，并探究如何改变点Q的速度（匀速运动），使四边形PDBQ在某一时刻为菱形，求点Q的速度；（3）如图2，在整个运动过程中，求出线段PQ的中点M所经过的路径长．图1 图24.如图1，在△ABC中，∠C＝90°，A C＝3，BC＝4，CD是斜边AB上的高，点E在斜边AB上，过点E 作直线与△ABC的直角边相交于点F，设AE＝x，△AEF的面积为y．（1）求线段AD的长；（2）若EF⊥AB，当点E在斜边AB上移动时，①求y与x的函数关系式（写出自变量x的取值范围）；②当x取何值时，y有最大值？并求出最大值．（3）若点F在直角边AC上（点F与A、C不重合），点E在斜边AB上移动，试问，是否存在直线EF将△ABC的周长和面积同时平分？若存在直线EF，求出x的值；若不存在直线EF，请说明理由．图1 备用图C 5. 如图，在等腰梯形ABCD 中，AB ∥DC ，cm BC AD 5==,AB =12 cm,CD =6cm , 点P 从A 开始沿AB 边向B 以每秒3cm 的速度移动，点Q 从C 开始沿CD 边向D 以每秒1cm 的速度移动，如果点P 、Q 分别从A 、C 同时出发，当其中一点到达终点时运动停止。

2012中考数学压轴题及答案1.（2011年四川省宜宾市）已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A （-1，0）、B （0，3）两点，其顶点为D.（1） 求该抛物线的解析式；（2） 若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积；（3） △AOB 与△BDE 是否相似？如果相似，请予以证明；如果不相似，请说明理由.（注：抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22）2. （11浙江衢州）已知直角梯形纸片OABC 在平面直角坐标系中的位置如图所示，四个顶点的坐标分别为O(0，0)，A(10，0)，B(8，32)，C(0，32)，点T 在线段OA 上(不与线段端点重合)，将纸片折叠，使点A 落在射线AB 上(记为点A ′)，折痕经过点T ，折痕TP 与射线AB 交于点P ，设点T 的横坐标为t ，折叠后纸片重叠部分(图中的阴影部分)的面积为S ；(1)求∠OAB 的度数，并求当点A ′在线段AB 上时，S 关于t 的函数关系式；(2)当纸片重叠部分的图形是四边形时，求t 的取值范围；(3)S 存在最大值吗？若存在，求出这个最大值，并求此时t 的值；若不存在，请说明理由.3. （11浙江温州）如图，在Rt ABC △中，90A ∠=，6AB =，8AC =，D E ，分别是边AB AC ，的中点，点P 从点D 出发沿DE 方向运动，过点P 作PQ BC ⊥于Q ，过点Q 作QR BA ∥交AC 于R ，当点Q 与点C 重合时，点P 停止运动．设BQ x =，QR y =．（1）求点D 到BC 的距离DH 的长；（2）求y 关于x 的函数关系式（不要求写出自变量的取值范围）；（3）是否存在点P ，使P Q R △为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由．4.（11山东省日照市）在△ABC 中，∠A ＝90°，AB ＝4，AC ＝3，M 是AB 上的动点（不与A ，B 重合），过M 点作MN ∥BC 交AC 于点N ．以MN 为直径作⊙O ，并在⊙O 内作内接矩形AMPN ．令AM ＝x ．（1）用含x 的代数式表示△ＭNP 的面积S ；（2）当x 为何值时，⊙O 与直线BC 相切？（3）在动点M 的运动过程中，记△ＭNP 与梯形BCNM 重合的面积为y ，试求y 关于x 的函数表达式，并求x 为何值时，y 的值最大，最大值是多少？5、（2007浙江金华）如图1，已知双曲线y=xk (k>0)与直线y=k ′x 交于A ，B 两点，点A 在第一象限.试解答下列问题：(1)若点A 的坐标为(4，2).则点B 的坐标为 ；若点A 的横坐标为m ，则点B 的坐标可表示为 ；（2）如图2，过原点O 作另一条直线l ，交双曲线y=xk (k>0)于P ，Q 两点，点P 在第一象限.①说明四边形APBQ 一定是平行四边形；②设点A.P 的横坐标分别为m ，n ，四边形APBQ 可能是矩形吗?可能是正方形吗?若可能，直接写出mn 应满足的条件；若不可能，请说明理由.8. (2011浙江义乌)如图1所示，直角梯形OABC 的顶点A 、C 分别在y 轴正半轴与x 轴负半轴上.过点B 、C 作直线l ．将直线l 平移，平移后的直线l 与x 轴交于点D ，与y 轴交于点E ．（1）将直线l 向右平移，设平移距离CD 为t (t ≥0)，直角梯形OABC 被直线l 扫过的面积（图中阴影部份）为s ，s 关于t 的函数图象如图2所示， OM 为线段，MN 为抛物线的一部分，NQ 为射线，N 点横坐标为4．①求梯形上底AB 的长及直角梯形OABC 的面积；②当42<<t 时，求S 关于t 的函数解析式；（2）在第（1）题的条件下，当直线l 向左或向右平移时（包括l 与直线BC 重合），在直线．．AB ．．上是否存在点P ，使PDE ∆为等腰直角三角形?若存在，请直接写出所有满足条件的点P 的坐标;若不存在，请说明理由．9.(2011山东烟台)如图，菱形ABCD 的边长为2，BD=2，E 、F 分别是边AD ，CD 上的两个动点，且满足AE+CF=2.（1）求证：△BDE ≌△BCF ；（2）判断△BEF 的形状，并说明理由；（3）设△BEF 的面积为S ，求S 的取值范围.10.(2011山东烟台)如图，抛物线21:23L y x x =--+交x 轴于A 、B 两点，交y 轴于M 点.抛物线1L 向右平移2个单位后得到抛物线2L ，2L 交x 轴于C 、D 两点.（1）求抛物线2L 对应的函数表达式；（2）抛物线1L 或2L 在x 轴上方的部分是否存在点N ，使以A ，C ，M ，N 为顶点的四边形是平行四边形.若存在，求出点N 的坐标；若不存在，请说明理由；（3）若点P 是抛物线1L 上的一个动点（P 不与点A 、B 重合），那么点P 关于原点的对称点Q 是否在抛物线2L 上，请说明理由.13.（2011山东威海）如图，在梯形ABCD 中，AB ∥CD ，AB ＝7，CD ＝1，AD ＝BC ＝5．点M ，N 分别在边AD ，BC 上运动，并保持MN ∥AB ，ME ⊥AB ，NF ⊥AB ，垂足分别为E ，F ．（1）求梯形ABCD 的面积；（2）求四边形MEFN 面积的最大值．（3）试判断四边形MEFN 能否为正方形，若能，求出正方形MEFN 的面积；若不能，请说明理由．16.(2011年浙江省绍兴市)将一矩形纸片OABC 放在平面直角坐标系中，(00)O ，，(60)A ，，(03)C ，．动点Q 从点O 出发以每秒1个单位长的速度沿OC 向终点C 运动，运动23秒时，动点P 从点A 出发以相等的速度沿AO 向终点O 运动．当其中一点到达终点时，另一点也停止运动．设点P 的运动时间为t （秒）． （1）用含t 的代数式表示OP OQ ，；（2）当1t 时，如图1，将OPQ △沿PQ 翻折，点O 恰好落在CB 边上的点D 处，求点D 的坐标；（4） 连结AC ，将OPQ △沿PQ 翻折，得到EPQ △，如图2．问：PQ 与AC 能否平行？PE 与AC能否垂直？若能，求出相应的t 值；若不能，说明理由．17.(2011年辽宁省十二市)如图16，在平面直角坐标系中，直线33y x =--与x 轴交于点A ，与y 轴交于点C ，抛物线223(0)3y ax x c a =-+≠经过A B C ，，三点． （1）求过A B C ，，三点抛物线的解析式并求出顶点F 的坐标；（2）在抛物线上是否存在点P ，使ABP △为直角三角形，若存在，直接写出P 点坐标；若不存在，请说明理由；（3）试探究在直线AC 上是否存在一点M ，使得MBF △的周长最小，若存在，求出M 点的坐标；若不存在，请说明理由．18.(2011年沈阳市)如图所示，在平面直角坐标系中，矩形ABOC 的边BO 在x 轴的负半轴上，边OC 在y 轴的正半轴上，且1AB =，3OB =，矩形ABOC 绕点O 按顺时针方向旋转60后得到矩形EFOD ．点A 的对应点为点E ，点B 的对应点为点F ，点C 的对应点为点D ，抛物线2y ax bx c =++过点A E D ，，．（1）判断点E 是否在y 轴上，并说明理由；（2）求抛物线的函数表达式；（3）在x 轴的上方是否存在点P ，点Q ，使以点O B P Q ，，，为顶点的平行四边形的面积是矩形ABOC 面积的2倍，且点P 在抛物线上，若存在，请求出点P ，点Q 的坐标；若不存在，请说明理由．19.(2011年四川省巴中市) 已知：如图14，抛物线2334y x =-+与x 轴交于点A ，点B ，与直线34y x b =-+相交于点B ，点C ，直线34y x b =-+与y 轴交于点E ． （1）写出直线BC 的解析式．（2）求ABC △的面积．（3）若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动（不与A B ，重合），同时，点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动．设运动时间为t 秒，请写出MNB △的面积S 与t 的函数关系式，并求出点M 运动多少时间时，MNB △的面积最大，最大面积是多少？20.(2011年成都市)如图，在平面直角坐标系xOy 中，△OAB 的顶点Ａ的坐标为（10，0），顶点B 在第一象限内，且AB =35，sin ∠OAB=55. （1）若点C 是点B 关于x 轴的对称点，求经过O 、C 、A 三点的抛物线的函数表达式；（2）在(1)中，抛物线上是否存在一点P ，使以P 、O 、C 、A 为顶点的四边形为梯形？若存在，求出点P 的坐标；若不存在，请说明理由；（3）若将点O 、点A 分别变换为点Q （ -2k ,0）、点R （5k ，0）（k>1的常数），设过Q 、R 两点，且以QR 的垂直平分线为对称轴的抛物线与y 轴的交点为N ，其顶点为M ，记△QNM 的面积为QMN S ∆，△QNR 的面积Q NR S ∆，求QMN S ∆∶Q NR S ∆的值.22.(2011年四川省宜宾市)已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A （-1，0）、B （0，3）两点，其顶点为D.(1)求该抛物线的解析式；(2)若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积；(3)△AOB 与△BDE 是否相似？如果相似，请予以证明；如果不相似，请说明理由.（注：抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22）．24.(2011年大庆市)如图①，四边形AEFG 和ABCD 都是正方形，它们的边长分别为a b ，（2b a ≥），且点F 在AD 上（以下问题的结果均可用a b ，的代数式表示）．（1）求DBF S △；（2）把正方形AEFG 绕点A 按逆时针方向旋转45°得图②，求图②中的DBF S △；（3）把正方形AEFG 绕点A 旋转一周，在旋转的过程中，DBF S △是否存在最大值、最小值？如果存在，直接写出最大值、最小值；如果不存在，请说明理由．25. （2011年上海市）已知24AB AD ==，，90DAB ∠=，AD BC ∥（如图13）．E 是射线BC 上的动点（点E 与点B 不重合），M 是线段DE 的中点．（1）设BE x ，ABM △的面积为y ，求y 关于x 的函数解析式，并写出函数的定义域；（2）如果以线段AB 为直径的圆与以线段DE 为直径的圆外切，求线段BE 的长；（3）联结BD ，交线段AM 于点N ，如果以A N D ，，为顶点的三角形与BME △相似，求线段BE 的长．27. （2011年山东省青岛市）已知：如图①，在Rt △ACB 中，∠C ＝90°，AC ＝4cm ，BC ＝3cm ，点P 由B 出发沿BA 方向向点A 匀速运动，速度为1cm/s ；点Q 由A 出发沿AC 方向向点C 匀速运动，速度为2cm/s ；连接PQ ．若设运动的时间为t （s ）（0＜t ＜2），解答下列问题：（1）当t 为何值时，PQ ∥BC ？（2）设△AQP 的面积为y （2cm ），求y 与t 之间的函数关系式；（3）是否存在某一时刻t ，使线段PQ 恰好把Rt △ACB 的周长和面积同时平分？若存在，求出此时t 的值；若不存在，说明理由；（4）如图②，连接PC ，并把△PQC 沿QC 翻折，得到四边形PQP ′C ，那么是否存在某一时刻t ，使四边形PQP ′C 为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．28.（2011年江苏省南通市）已知双曲线kyx=与直线14y x=相交于A、B两点.第一象限上的点M（m，n）（在A点左侧）是双曲线kyx=上的动点.过点B作BD∥y轴于点D.过N（0，－n）作NC∥x轴交双曲线kyx=于点E，交BD于点C.（1）若点D坐标是（－8，0），求A、B两点坐标及k的值.（2）若B是CD的中点，四边形OBCE的面积为4，求直线CM的解析式.（3）设直线AM、BM分别与y轴相交于P、Q两点，且MA＝pMP，MB＝qMQ，求p－q的值.29.（2011年江苏省无锡市）一种电讯信号转发装置的发射直径为31km．现要求：在一边长为30km的正方形城区选择若干个安装点，每个点安装一个这种转发装置，使这些装置转发的信号能完全覆盖这个城市．问：（1）能否找到这样的4个安装点，使得这些点安装了这种转发装置后能达到预设的要求？（2）至少需要选择多少个安装点，才能使这些点安装了这种转发装置后达到预设的要求？答题要求：请你在解答时，画出必要的示意图，并用必要的计算、推理和文字来说明你的理由．（下面给出了几个边长为30km的正方形城区示意图，供解题时选用）压轴题答案1.解：（ 1）由已知得：310c b c =⎧⎨--+=⎩解得c=3,b =2∴抛物线的线的解析式为223y x x =-++(2)由顶点坐标公式得顶点坐标为（1，4）所以对称轴为x=1,A,E 关于x=1对称，所以E(3,0)设对称轴与x 轴的交点为F所以四边形ABDE 的面积=ABO DFE BOFD S S S ∆∆++梯形 =111()222AO BO BO DF OF EF DF ⋅++⋅+⋅ =11113(34)124222⨯⨯++⨯+⨯⨯ =9 （3）相似如图，BD=2222112BG DG +=+= BE=22223332BO OE +=+= DE=22222425DF EF +=+=所以2220BD BE +=, 220DE =即： 222BD BE DE +=,所以BDE ∆是直角三角形 所以90AOB DBE ∠=∠=︒,且22AO BO BD BE ==, 所以AOB DBE ∆∆.2. (1) ∵A ，B 两点的坐标分别是A(10，0)和B(8，32)，∴381032OAB tan =-=∠， ∴︒=∠60OAB当点A ´在线段AB 上时，∵︒=∠60OAB ，TA=TA ´，∴△A ´TA 是等边三角形，且A T TP '⊥，∴)t 10(2360sin )t 10(T P -=︒-=，)t 10(21AT 21AP P A -==='，○2当6t 2<≤时，由图○1，重叠部分的面积EB A TP A S S S '∆'∆-=∵△A ´EB 的高是︒'60sin B A ， ∴23)4t 10(21)t 10(83S 22⨯----= 34)2t (83)28t 4t (8322+--=++-=当t=2时，S 的值最大是34；○3当2t 0<<，即当点A ´和点P 都在线段AB 的延长线是(如图○2，其中E 是TA ´与CB 的交点，F 是TP 与CB 的交点)，∵ETF FTP EFT ∠=∠=∠，四边形ETAB 是等腰形，∴EF=ET=AB=4， ∴3432421OC EF 21S =⨯⨯=⋅= 综上所述，S 的最大值是34，此时t 的值是2t 0≤<.3. 解：（1）Rt A ∠=∠，6AB =，8AC =，10BC ∴=．点D 为AB 中点，132BD AB ∴==． 90DHB A ∠=∠=，B B ∠=∠．BHD BAC ∴△∽△，DH BD AC BC ∴=，3128105BD DH AC BC ∴==⨯=． （2）QR AB ∥，90QRC A ∴∠=∠=． C C ∠=∠，RQC ABC ∴△∽△，RQ QC AB BC ∴=，10610y x -∴=， 即y 关于x 的函数关系式为：365y x =-+． （3）存在，分三种情况：①当PQ PR =时，过点P 作PM QR ⊥于M ，则QM RM =．1290∠+∠=，290C ∠+∠=，1C ∴∠=∠．84cos 1cos 105C ∴∠===，45QM QP ∴=， 1364251255x ⎛⎫-+ ⎪⎝⎭∴=，185x ∴=． ②当PQ RQ =时，312655x -+=， 6x ∴=．③当PR QR =时，则R 为PQ 中垂线上的点，于是点R 为EC 的中点，11224CR CE AC ∴===． tan QR BA C CR CA ==， 366528x -+∴=，152x ∴=． 综上所述，当x 为185或6或152时，PQR △为等腰三角形．4.解：（1）∵MN ∥BC ，∴∠AMN =∠B ，∠ANM ＝∠C ．∴ △AMN ∽ △ABC ．∴ AM AN AB AC =，即43x AN =． ∴ AN ＝43x ． ……………2分 ∴ S =2133248MNP AMN S S x x x ∆∆==⋅⋅=．（0＜x ＜4） ……………3分 （2）如图2，设直线BC 与⊙O 相切于点D ，连结AO ，OD ，则AO =OD =21MN ．在Rt △ABC 中，BC ＝22AB AC +=5．由（1）知 △AMN ∽ △ABC ．∴ AM MN AB BC =，即45x MN =． ∴ 54MN x =， ∴ 58OD x =． …………………5分 过M 点作MQ ⊥BC 于Q ，则58MQ OD x ==． 在Rt △BMQ 与Rt △BCA 中，∠B 是公共角，∴ △BMQ ∽△BCA ．∴ BM QM BC AC=． ∴ 55258324x BM x ⨯==，25424AB BM MA x x =+=+=．∴ x ＝4996． ∴ 当x ＝4996时，⊙O 与直线B C 相切．…………………………………7分故以下分两种情况讨论：① 当0＜x ≤2时，2Δ83x S y PMN ==． ∴ 当x ＝2时，2332.82y =⨯=最大 ……………………………………8分② 当2＜x ＜4时，设PM ，PN 分别交BC 于E ，F ．∵ 四边形AMPN 是矩形，∴ PN ∥AM ，PN ＝AM ＝x ．又∵ MN ∥BC ，∴ 四边形MBFN 是平行四边形．∴ FN ＝BM ＝4－x ．∴ ()424PF x x x =--=-．又△PEF ∽ △ACB ．∴ 2PEF ABC S PF AB S ∆∆⎛⎫= ⎪⎝⎭． ∴ ()2322PEF S x ∆=-． ……………………………………………… 9分 MNP PEF y S S ∆∆=-＝()222339266828x x x x --=-+-．……………………10分 当2＜x ＜4时，29668y x x =-+-298283x ⎛⎫=--+ ⎪⎝⎭． ∴ 当83x =时，满足2＜x ＜4，2y =最大． ……………………11分 综上所述，当83x =时，y 值最大，最大值是2． …………………………12分 5. 解：（1）（-4，-2）；（-m,-k m） (2) ①由于双曲线是关于原点成中心对称的，所以OP=OQ,OA=OB,所以四边形APBQ一定是平行四边形②可能是矩形，mn=k 即可不可能是正方形，因为Op 不能与OA 垂直.解：（1）作BE ⊥OA ，∴ΔAOB 是等边三角形∴BE=OB ·sin60o =23，∴B(23,2)∵A(0,4),设AB 的解析式为4y kx =+,所以2342k +=,解得33k =-,的以直线AB 的解析式为 343y x =-+（2）由旋转知，AP=AD, ∠PAD=60o, ∴ΔAPD 是等边三角形，PD=PA=2219AO OP +=6. 解：（1）作BE ⊥OA ，∴ΔAOB 是等边三角形∴BE=OB ·sin60o =23，∴B(23,2)∵A(0,4),设AB 的解析式为4y kx =+,所以2342k +=,解得33k =-, 以直线AB 的解析式为343y x =-+ （2）由旋转知，AP=AD, ∠PAD=60o ,∴ΔAPD 是等边三角形，PD=PA=2219AO OP +=（1）①2AB = ……………………………………………………………………………2分842OA ==，4OC =，S 梯形OABC =12 ……………………………………………2分 ②当42<<t 时，直角梯形OABC 被直线l 扫过的面积=直角梯形OABC 面积－直角三角开DOE 面积2112(4)2(4)842S t t t t =--⨯-=-+-…………………………………………4分（2） 存在 ……………………………………………………………………………………1分123458(12,4),(4,4),(,4),(4,4),(8,4)3P P P P P --- …（每个点对各得1分）……5分 对于第（2）题我们提供如下详细解答（评分无此要求）.下面提供参考解法二： ① 以点D 为直角顶点，作1PP x ⊥轴同理在③二图中分别可得P点的生标为P（－4，4）（与①情形二重合舍去）、P（4，4），E点在A点下方不可能.综上可得P点的生标共5个解，分别为P（－12，4）、P（－4，4）、P（－83，4）、P（8，4）、P（4，4）．下面提供参考解法二：以直角进行分类进行讨论（分三类）： 第一类如上解法⑴中所示图22P DE y x b ∠=+为直角：设直线：，D 此时（-b,o)，E(O,2b) 的中点坐标为b (-,b)2，直线DE 的中垂线方程：1()22by b x -=-+，令4y =得3(8,4)2b P -．由已知可得2PE DE =即222232(8)(42)42b b b b ⨯-+-=+化简得2332640b b -+=解得 121883b b P P ==∴=3b，将之代入（-8，4）（4，4)、22(4,4)P -；第二类如上解法②中所示图22E DE y x b ∠=+为直角：设直线：，D 此时（-b,o)，E(O,2b) ，直线PE 的方程：122y x b =-+，令4y =得(48,4)P b -．由已知可得PE DE =即2222(48)(42)4b b b b -+-=+化简得22(28)b b =-解之得 ，123443b b P P ==∴=，将之代入（4b-8，4）（8，4)、48(,4)3P - 第三类如上解法③中所示图22D DE y x b ∠=+为直角：设直线：，D 此时（-b,o)，E(O,2b) ，直线PD 的方程：1()2y x b =-+，令4y =得(8,4)P b --．由已知可得PD DE =即2222844b b +=+解得12544b b P P ==-∴=，将之代入（-b-8，4）（-12，4)、 6(4,4)P -（6(4,4)P -与2P 重合舍去）．综上可得P 点的生标共5个解，分别为P （－12，4）、P （－4，4）、P （－83，4）、 P （8，4）、P （4，4）．事实上，我们可以得到更一般的结论：如果得出AB a OC b ==、、OA h =、设b ak h-=，则P 点的情形如下∴ 6494738)2(7342+⎪⎭⎫ ⎝⎛--=-=⋅=x x x EF ME S MEFN矩形． ……………………8分当x ＝47时，ME ＝37＜4，∴四边形MEFN 面积的最大值为649．……………9分（3）能． ……………………………………………………………………10分 由（2）可知，设AE ＝x ，则EF ＝7－2x ，ME ＝x 34． 若四边形MEFN 为正方形，则ME ＝EF ． 即=34x 7－2x ．解，得 1021=x ． ……………………………………………11分 ∴ EF ＝21147272105x -=-⨯=＜4． ∴ 四边形MEFN 能为正方形，其面积为251965142=⎪⎭⎫ ⎝⎛=MEFNS 正方形． ∴ 6494738)2(7342+⎪⎭⎫ ⎝⎛--=-=⋅=x x x EF ME S MEFN矩形． ……………………8分当x ＝47时，ME ＝37＜4，∴四边形MEFN 面积的最大值为649．……………9分（3）能． ……………………………………………………………………10分 由（2）可知，设AE ＝x ，则EF ＝7－2x ，ME ＝x 34． 若四边形MEFN 为正方形，则ME ＝EF ． 即=34x 7－2x ．解，得 1021=x ． ……………………………………………11分 ∴ EF ＝21147272105x -=-⨯=＜4． ∴ 四边形MEFN 能为正方形，其面积为251965142=⎪⎭⎫ ⎝⎛=MEFN S 正方形．（2）当1t =时，过D 点作1DD OA ⊥，交OA 于1D ，如图1， 则53DQ QO ==，43QC =，1CD ∴=，(13)D ∴，．（3）①PQ 能与AC 平行．若PQ AC ∥，如图2，则OP OAOQ OC=， 即66233t t -=+，149t ∴=，而703t ≤≤， 149t ∴=． ②PE 不能与AC 垂直．若PE AC ⊥，延长QE 交OA 于F ，如图3，则23335t QF OQ QFAC OC +==．253QF t ⎛⎫∴=+ ⎪⎝⎭．EF QF QE QF OQ ∴=-=-22533t t ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭2(51)(51)3t =-+-．又Rt Rt EPF OCA △∽△，PE OCEF OA∴=， 6326(51)3t t -∴=⎛⎫-+ ⎪⎝⎭，3.45t ∴≈，而703t ≤≤，t ∴不存在．17. 解：（1）直线33y x =--与x 轴交于点A ，与y 轴交于点C ．(10)A ∴-，，(03)C -， ··························································································· 1分 点A C ，都在抛物线上，23033a c c ⎧=++⎪∴⎨⎪-=⎩ 333a c ⎧=⎪∴⎨⎪=-⎩∴抛物线的解析式为2323333y x x =-- ·························································· 3分 ∴顶点4313F ⎛⎫- ⎪ ⎪⎝⎭， ································································································ 4分 （2）存在 ················································································································ 5分 1(03)P -， ·············································································································· 7分2(23)P -， ·············································································································· 9分 （3）存在 ·············································································································· 10分 理由： 解法一：延长BC 到点B '，使BC B C '=，连接B F '交直线AC 于点M ，则点M 就是所求的点．····················································································· 11分在Rt BB H '△中，1232B H BB ''==， 36BH B H '==，3OH ∴=，(323)B '∴--， ·················································· 12分 设直线B F '的解析式为y kx b =+233433k b k b ⎧-=-+⎪∴⎨-=+⎪⎩ 解得36332k b ⎧=⎪⎪⎨⎪=-⎪⎩33362y x ∴=- ································································································· 13分 3333362y x y x ⎧=--⎪∴⎨=-⎪⎩ 解得371037x y ⎧=⎪⎪⎨⎪=-⎪⎩，310377M ⎛⎫∴- ⎪ ⎪⎝⎭，∴在直线AC 上存在点M ，使得MBF △的周长最小，此时310377M ⎛⎫- ⎪ ⎪⎝⎭，． ····· 14分03533k b b =+⎧⎪⎨=-⎪⎩ 解得539533k b ⎧=⎪⎪⎨⎪=-⎪⎩ 553393y ∴=- ································································································· 13分 55339333y x y x ⎧=-⎪∴⎨⎪=--⎩ 解得371037x y ⎧=⎪⎪⎨⎪=-⎪⎩310377M ⎛⎫∴- ⎪ ⎪⎝⎭， ∴在直线AC 上存在点M ，使得MBF △的周长最小，此时310377M ⎛⎫- ⎪ ⎪⎝⎭，． 1 18. 解：（1）点E 在y 轴上 ···················································································· 1分 理由如下：连接AO ，如图所示，在Rt ABO △中，1AB =，3BO =，2AO ∴=1sin 2AOB ∴∠=，30AOB ∴∠= 由题意可知：60AOE ∠=306090BOE AOB AOE ∴∠=∠+∠=+=点B 在x 轴上，∴点E 在y 轴上． ······································································· 3分（2）过点D 作DM x ⊥轴于点M1OD =，30DOM ∠=∴在Rt DOM △中，12DM =，32OM = 点D 在第一象限， ∴点D 的坐标为3122⎛⎫ ⎪ ⎪⎝⎭， ························································································ 5分 由（1）知2EO AO ==，点E 在y 轴的正半轴上∴点E 的坐标为(02)，∴点A 的坐标为(31)-， ·························································································· 6分 抛物线2y ax bx c =++经过点E ，2c ∴= 由题意，将(31)A -，，3122D ⎛⎫ ⎪ ⎪⎝⎭，代入22y ax bx =++中得33213312422a b a b ⎧-+=⎪⎨++=⎪⎩ 解得89539a b ⎧=-⎪⎪⎨⎪=-⎪⎩∴所求抛物线表达式为：2853299y x x =--+ ······················································ 9分 （3）存在符合条件的点P ，点Q ． ······································································ 10分 理由如下：矩形ABOC 的面积3AB BO ==∴以O B P Q ，，，为顶点的平行四边形面积为23．由题意可知OB 为此平行四边形一边， 又3OB =OB ∴边上的高为2 ································································································ 11分依题意设点P 的坐标为(2)m ， 点P 在抛物线2853299y x x =--+上 28532299m m ∴--+= 解得，10m =，2538m =-1(02)P ∴，，25328P ⎛⎫- ⎪ ⎪⎝⎭，以O B P Q ，，，为顶点的四边形是平行四边形，PQ OB ∴∥，3PQ OB ==，∴当点1P 的坐标为(02)，时， 点Q 的坐标分别为1(32)Q -，，2(32)Q ，；当点2P 的坐标为5328⎛⎫- ⎪ ⎪⎝⎭，时，点Q 的坐标分别为313328Q ⎛⎫-⎪ ⎪⎝⎭，，43328Q ⎛⎫ ⎪ ⎪⎝⎭，． ·············································· 14分 （以上答案仅供参考，如有其它做法，可参照给分）19.解：（1）在2334y x =-+中，令0y = 23304x ∴-+=12x ∴=，22x =-(20)A ∴-，，(20)B ， ··················································· 1分 又点B 在34y x b =-+上 302b ∴=-+ 32b = BC ∴的解析式为3342y x =-+ ················································································ 2分 （2）由23343342y x y x ⎧=-+⎪⎪⎨⎪=-+⎪⎩，得11194x y =-⎧⎪⎨=⎪⎩ 2220x y =⎧⎨=⎩ ······················································· 4分 914C ⎛⎫∴- ⎪⎝⎭，，(20)B ， 4AB ∴=，94CD = ································································································ 5分 1994242ABC S ∴=⨯⨯=△ ··························································································· 6分 （3）过点N 作NP MB ⊥于点PEO MB ⊥NP EO ∴∥BNP BEO ∴△∽△ ································································································· 7分 BN NP BE EO∴= ··········································································································· 8分 由直线3342y x =-+可得：302E ⎛⎫ ⎪⎝⎭，∴在BEO △中，2BO =，32EO =，则52BE = 25322t NP ∴=，65NP t ∴= ························································································· 9分 16(4)25S t t ∴=- 2312(04)55S t t t =-+<< ······················································································ 10分 2312(2)55S t =--+ ······························································································· 11分 此抛物线开口向下，∴当2t =时，125S =最大 ∴当点M 运动2秒时，MNB △的面积达到最大，最大为125． 20. 解：（1）如图，过点B 作BD ⊥OA 于点D.在Rt △ABD 中，∵∣AB ∣=35,sin ∠OAB=55, ∴∣BD ∣=∣AB ∣·sin ∠OAB =35×55=3. 又由勾股定理，得22A D AB B D =- 22(35)36=-=∴∣OD ∣=∣OA ∣-∣AD ∣=10-6=4.∵点B 在第一象限，∴点B 的坐标为（4，3）. ……3分。

2013年中考数学压轴题及解析分类汇编2013年中考数学压轴题及解析分类汇编2013中考数学压轴：相似三角形问题2013中考数学压轴题函数相似三角形问题(一)2013中考数学压轴题函数相似三角形问题(二)2013中考数学压轴题函数相似三角形问题(三)2013中考数学压轴：等腰三角形问题2013中考数学压轴题函数等腰三角形问题(一)2013中考数学压轴题函数等腰三角形问题(二)2013中考数学压轴题函数等腰三角形问题(三)2013中考数学压轴：直角三角形问题2013中考数学压轴题函数直角三角形问题(一)2013中考数学压轴题函数直角三角形问题(二)2013中考数学压轴题函数直角三角形问题(三)2013中考数学压轴：平行四边形问题2013中考数学压轴题函数平行四边形问题(一)2013中考数学压轴题函数平行四边形问题(二)2013中考数学压轴题函数平行四边形问题(三)2013中考数学压轴：梯形问题2013中考数学压轴题函数梯形问题(一)2013中考数学压轴题函数梯形问题(二)2013中考数学压轴题函数梯形问题(三)2013中考数学压轴：面积问题2013中考数学压轴题函数面积问题(一)2013中考数学压轴题函数面积问题(二)2013中考数学压轴题函数面积问题(三)2013中考数学压轴题:函数相似三角形问题(一) 例1直线113y x=-+分别交x轴、y轴于A、B两点，△AOB绕点O按逆时针方向旋转90°后得到△COD，抛物线y＝ax2＋bx＋c经过A、C、D三点．(1) 写出点A、B、C、D的坐标；(2) 求经过A、C、D三点的抛物线表达式，并求抛物线顶点G的坐标；(3) 在直线BG上是否存在点Q，使得以点A、B、Q为顶点的三角形与△COD相似？若存在，请求出点Q的坐标；若不存在，请说明理由．图1动感体验请打开几何画板文件名“11闸北25”，拖动点Q在直线BG上运动，可以体验到，△ABQ的两条直角边的比为1∶3共有四种情况，点B上、下各有两种．思路点拨1．图形在旋转过程中，对应线段相等，对应角相等，对应线段的夹角等于旋转角．2．用待定系数法求抛物线的解析式，用配方法求顶点坐标．3．第（3）题判断∠ABQ＝90°是解题的前提．4．△ABQ与△COD相似，按照直角边的比分两种情况，每种情况又按照点Q与点B的位置关系分上下两种情形，点Q共有4个．满分解答（1）A (3，0)，B (0，1)，C (0，3)，D (－1，0)．（2）因为抛物线y ＝ax 2＋bx ＋c 经过A (3，0)、C (0，3)、D (－1，0) 三点，所以930,3,0.a b c c a b c ++=⎧⎪=⎨⎪-+=⎩ 解得1,2,3.a b c =-⎧⎪=⎨⎪=⎩所以抛物线的解析式为y ＝－x 2＋2x ＋3＝－(x －1)2＋4，顶点G 的坐标为(1，4)．（3）如图2，直线BG 的解析式为y ＝3x ＋1，直线CD 的解析式为y ＝3x ＋3，因此CD //BG ．因为图形在旋转过程中，对应线段的夹角等于旋转角，所以AB ⊥CD ．因此AB ⊥BG ，即∠ABQ ＝90°．因为点Q 在直线BG 上，设点Q 的坐标为(x ，3x ＋1)，那么22(3)10BQ x x x =+=±． Rt △COD 的两条直角边的比为1∶3，如果Rt △ABQ 与Rt △COD 相似，存在两种情况：①当3BQ BA =时，10310x ±=．解得3x =±．所以1(3,10)Q ，2(3,8)Q --． ②当13BQ BA =时，101310x ±=．解得13x =±．所以31(,2)3Q ，41(,0)3Q -．图2 图3考点伸展第（3）题在解答过程中运用了两个高难度动作：一是用旋转的性质说明AB ⊥BG ；二是BQ ==．我们换个思路解答第（3）题：如图3，作GH ⊥y 轴，QN ⊥y 轴，垂足分别为H 、N ．通过证明△AOB ≌△BHG ，根据全等三角形的对应角相等，可以证明∠ABG ＝90°． 在Rt △BGH 中，sin 1∠=cos 1∠=①当3BQ BA=时，BQ =． 在Rt △BQN 中，sin 13QN BQ =⋅∠=，cos 19BN BQ =⋅∠=．当Q 在B 上方时，1(3,10)Q ；当Q 在B 下方时，2(3,8)Q --．②当13BQ BA =时，BQ =31(,2)3Q ，41(,0)3Q -．例2Rt △ABC 在直角坐标系内的位置如图1所示，反比例函数(0)k y k x=≠在第一象限内的图像与BC 边交于点D （4，m ），与AB 边交于点E （2，n ），△BDE 的面积为2．（1）求m 与n 的数量关系；（2）当tan ∠A ＝12时，求反比例函数的解析式和直线AB 的表达式； （3）设直线AB 与y 轴交于点F ，点P 在射线FD 上，在（2）的条件下，如果△AEO 与△EFP 相似，求点P 的坐标．图1动感体验请打开几何画板文件名“11杨浦24”，拖动点A 在x 轴上运动，可以体验到，直线AB 保持斜率不变，n 始终等于m 的2倍，双击按钮“面积BDE ＝2”，可以看到，点E 正好在BD 的垂直平分线上，FD //x 轴．拖动点P 在射线FD 上运动，可以体验到，△AEO 与△EFP 相似存在两种情况．思路点拨1．探求m 与n 的数量关系，用m 表示点B 、D 、E 的坐标，是解题的突破口．2．第（2）题留给第（3）题的隐含条件是FD //x 轴．3．如果△AEO 与△EFP 相似，因为夹角相等，根据对应边成比例，分两种情况． 满分解答（1）如图1，因为点D （4，m ）、E （2，n ）在反比例函数k y x=的图像上，所以4,2.m k n k =⎧⎨=⎩ 整理，得n ＝2m ． （2）如图2，过点E 作EH ⊥BC ，垂足为H ．在Rt △BEH 中，tan ∠BEH ＝tan ∠A ＝12，EH ＝2，所以BH ＝1．因此D (4，m )，E (2，2m )，B (4，2m ＋1)． 已知△BDE 的面积为2，所以11(1)2222BD EH m ⋅=+⨯=．解得m ＝1．因此D (4，1)，E (2，2)，B (4，3)． 因为点D （4，1）在反比例函数k y x =的图像上，所以k ＝4．因此反比例函数的解析式为4y x=．设直线AB的解析式为y＝kx＋b，代入B(4，3)、E(2，2)，得34,22.k bk b=+⎧⎨=+⎩解得12k=，1 b=．因此直线AB的函数解析式为112y x=+．图2 图3 图4（3）如图3，因为直线112y x=+与y轴交于点F（0，1），点D的坐标为（4，1），所以FD// x轴，∠EFP＝∠EAO．因此△AEO与△EFP相似存在两种情况：①如图3，当EA EFAO FP=时，255=．解得FP＝1．此时点P的坐标为（1，1）．②如图4，当EA FPAO EF=时，255=．解得FP＝5．此时点P的坐标为（5，1）．考点伸展本题的题设部分有条件“Rt△ABC在直角坐标系内的位置如图1所示”，如果没有这个条件限制，保持其他条件不变，那么还有如图5的情况：第（1）题的结论m与n的数量关系不变．第（2）题反比例函数的解析式为12yx=-，直线AB为172y x=-．第（3）题FD不再与x轴平行，△AEO与△EFP也不可能相似．图52013中考数学压轴题函数相似三角形问题(二) 例3如图1，已知梯形OABC，抛物线分别过点O（0，0）、A（2，0）、B（6，3）．（1）直接写出抛物线的对称轴、解析式及顶点M的坐标；（2）将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移，分别交抛物线于点O1、A1、C1、B1，得到如图2的梯形O1A1B1C1．设梯形O1A1B1C1的面积为S，A1、B1的坐标分别为(x1，y1)、(x2，y2)．用含S的代数式表示x2－x1，并求出当S=36时点A1的坐标；（3）在图1中，设点D的坐标为(1，3)，动点P从点B出发，以每秒1个单位长度的速度沿着线段BC运动，动点Q从点D出发，以与点P相同的速度沿着线段DM运动．P、Q两点同时出发，当点Q到达点M时，P、Q两点同时停止运动．设P、Q两点的运动时间为t，是否存在某一时刻t，使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似？若存在，请求出t的值；若不存在，请说明理由．图1 图2动感体验请打开几何画板文件名“10义乌24”，拖动点I上下运动，观察图形和图像，可以体验到，x2－x1随S的增大而减小．双击按钮“第（3）题”，拖动点Q在DM上运动，可以体验到，如果∠GAF＝∠GQE，那么△GAF与△GQE相似．思路点拨1．第（2）题用含S 的代数式表示x 2－x 1，我们反其道而行之，用x 1，x 2表示S ．再注意平移过程中梯形的高保持不变，即y 2－y 1＝3．通过代数变形就可以了．2．第（3）题最大的障碍在于画示意图，在没有计算结果的情况下，无法画出准确的位置关系，因此本题的策略是先假设，再说理计算，后验证．3．第（3）题的示意图，不变的关系是：直线AB 与x 轴的夹角不变，直线AB 与抛物线的对称轴的夹角不变．变化的直线PQ 的斜率，因此假设直线PQ 与AB 的交点G 在x 轴的下方，或者假设交点G 在x 轴的上方．满分解答（1）抛物线的对称轴为直线1x =，解析式为21184y x x =-，顶点为M （1，18-）． （2） 梯形O 1A 1B 1C 1的面积12122(11)3()62x x S x x -+-⨯3==+-，由此得到1223s x x +=+．由于213y y -=，所以22212211111138484y y x x x x -=--+=．整理，得212111()()384x x x x ⎡⎤-+-=⎢⎥⎣⎦．因此得到2172x x S -=． 当S =36时，212114,2.x x x x +=⎧⎨-=⎩ 解得126,8.x x =⎧⎨=⎩ 此时点A 1的坐标为（6，3）． （3）设直线AB 与PQ 交于点G ，直线AB 与抛物线的对称轴交于点E ，直线PQ 与x 轴交于点F ，那么要探求相似的△GAF 与△GQE ，有一个公共角∠G ．在△GEQ 中，∠GEQ 是直线AB 与抛物线对称轴的夹角，为定值．在△GAF 中，∠GAF 是直线AB 与x 轴的夹角，也为定值，而且∠GEQ ≠∠GAF ． 因此只存在∠GQE ＝∠GAF 的可能，△GQE ∽△GAF ．这时∠GAF ＝∠GQE ＝∠PQD ． 由于3tan 4GAF ∠=，tan 5DQ t PQD QP t ∠==-，所以345t t =-．解得207t =．图3 图4 考点伸展第（3）题是否存在点G 在x 轴上方的情况？如图4，假如存在，说理过程相同，求得的t 的值也是相同的．事实上，图3和图4都是假设存在的示意图，实际的图形更接近图3．例4如图1，已知点A (-2，4) 和点B (1，0)都在抛物线22y mx mx n =++上．（1）求m 、n ；（2）向右平移上述抛物线，记平移后点A 的对应点为A ′，点B 的对应点为B ′，若四边形A A ′B ′B 为菱形，求平移后抛物线的表达式；（3）记平移后抛物线的对称轴与直线AB ′ 的交点为C ，试在x 轴上找一个点D ，使得以点B ′、C 、D 为顶点的三角形与△ABC 相似．图1动感体验请打开几何画板文件名“10宝山24”，拖动点A ′向右平移，可以体验到，平移5个单位后，四边形A A ′B ′B 为菱形．再拖动点D 在x 轴上运动，可以体验到，△B ′CD 与△ABC 相似有两种情况．思路点拨1．点A 与点B 的坐标在3个题目中处处用到，各具特色．第（1）题用在待定系数法中；第（2）题用来计算平移的距离；第（3）题用来求点B ′ 的坐标、AC 和B ′C 的长．2．抛物线左右平移，变化的是对称轴，开口和形状都不变．3．探求△ABC 与△B ′CD 相似，根据菱形的性质，∠BAC ＝∠CB ′D ，因此按照夹角的两边对应成比例，分两种情况讨论．满分解答(1) 因为点A (-2，4) 和点B (1，0)都在抛物线22y mx mx n =++上，所以444,20.m m n m m n -+=⎧⎨++=⎩ 解得43m =-，4n =． (2)如图2，由点A (-2，4) 和点B (1，0)，可得AB ＝5．因为四边形A A ′B ′B 为菱形，所以A A ′＝B ′B ＝ AB ＝5．因为438342+--=x x y ()2416133x =-++，所以原抛物线的对称轴x ＝－1向右平移5个单位后，对应的直线为x ＝4．因此平移后的抛物线的解析式为()3164342,+--=x y ．图2(3) 由点A (-2，4) 和点B′(6，0)，可得A B′＝45．如图2，由AM//CN，可得''''B N B CB M B A=，即2845=．解得'5B C=．所以35AC=．根据菱形的性质，在△ABC与△B′CD中，∠BAC＝∠CB′D．①如图3，当''AB B CAC B D=时，535=，解得'3B D=．此时OD＝3，点D的坐标为（3，0）．②如图4，当''AB B DAC B C=时，355=，解得5'3B D=．此时OD＝133，点D的坐标为（133，0）．图3 图4考点伸展在本题情境下，我们还可以探求△B′CD与△AB B′相似，其实这是有公共底角的两个等腰三角形，容易想象，存在两种情况．我们也可以讨论△B′CD与△C B B′相似，这两个三角形有一组公共角∠B，根据对应边成比例，分两种情况计算．2013中考数学压轴题函数相似三角形问题(三) 例5如图1，抛物线经过点A(4，0)、B（1，0)、C（0，－2）三点．（1）求此抛物线的解析式；（2）P是抛物线上的一个动点，过P作PM⊥x轴，垂足为M，是否存在点P，使得以A、P、M为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由；（3）在直线AC上方的抛物线是有一点D，使得△DCA的面积最大，求出点D的坐标．,图1动感体验请打开几何画板文件名“09临沂26”，拖动点P在抛物线上运动，可以体验到，△PAM的形状在变化，分别双击按钮“P在B左侧”、“P在x轴上方”和“P在A右侧”，可以显示△PAM与△OAC相似的三个情景．双击按钮“第(3)题”，拖动点D在x轴上方的抛物线上运动，观察△DCA的形状和面积随D变化的图象，可以体验到，E是AC的中点时，△DCA的面积最大．思路点拨1．已知抛物线与x轴的两个交点，用待定系数法求解析式时，设交点式比较简便．2．数形结合，用解析式表示图象上点的坐标，用点的坐标表示线段的长． 3．按照两条直角边对应成比例，分两种情况列方程． 4．把△DCA 可以分割为共底的两个三角形，高的和等于OA ．满分解答（1）因为抛物线与x 轴交于A (4，0)、B （1，0)两点，设抛物线的解析式为)4)(1(--=x x a y ，代入点C 的 坐标（0，－2），解得21-=a ．所以抛物线的解析式为22521)4)(1(212-+-=---=x x x x y ．（2）设点P 的坐标为))4)(1(21,(---x x x ．①如图2，当点P 在x 轴上方时，1＜x ＜4，)4)(1(21---=x x PM ，x AM -=4．如果2==CO AO PM AM ，那么24)4)(1(21=----x x x ．解得5=x 不合题意．如果21==CO AO PM AM ，那么214)4)(1(21=----x x x ．解得2=x ．此时点P 的坐标为（2，1）．②如图3，当点P 在点A 的右侧时，x ＞4，)4)(1(21--=x x PM ，4-=x AM ．解方程24)4)(1(21=---x x x ，得5=x ．此时点P 的坐标为)2,5(-．解方程214)4)(1(21=---x x x ，得2=x 不合题意．③如图4，当点P 在点B 的左侧时，x ＜1，)4)(1(21--=x x PM ，x AM -=4． 解方程24)4)(1(21=---xx x ，得3-=x ．此时点P 的坐标为)14,3(--．解方程214)4)(1(21=---xxx，得0=x．此时点P与点O重合，不合题意．综上所述，符合条件的点P的坐标为（2，1）或)14,3(--或)2,5(-．图2 图3 图4（3）如图5，过点D作x轴的垂线交AC于E．直线AC的解析式为221-=xy．设点D的横坐标为m)41(<<m，那么点D的坐标为)22521,(2-+-mmm，点E的坐标为)221,(-mm．所以)221()22521(2---+-=mmmDE mm2212+-=．因此4)221(212⨯+-=∆mmSDACmm42+-=4)2(2+--=m．当2=m时，△DCA的面积最大，此时点D的坐标为（2，1）．图5 图6第（3）题也可以这样解：如图6，过D 点构造矩形OAMN ，那么△DCA 的面积等于直角梯形CAMN 的面积减去△CDN 和△ADM 的面积．设点D 的横坐标为（m ，n ）)41(<<m ，那么42)4(21)2(214)22(21++-=--+-⨯+=n m m n n m n S ． 由于225212-+-=m m n ，所以m m S 42+-=． 例6如图1，△ABC 中，AB ＝5，AC ＝3，cos A ＝310．D 为射线BA 上的点（点D 不与点B 重合），作DE //BC 交射线CA 于点E .．(1) 若CE ＝x ，BD ＝y ，求y 与x 的函数关系式，并写出函数的定义域； (2) 当分别以线段BD ，CE 为直径的两圆相切时，求DE 的长度；(3) 当点D 在AB 边上时，BC 边上是否存在点F ，使△ABC 与△DEF 相似？若存在，请求出线段BF 的长；若不存在，请说明理由．图1 备用图 备用图动感体验请打开几何画板文件名“09闸北25”，拖动点D 可以在射线BA 上运动．双击按钮“第（2）题”，拖动点D 可以体验到两圆可以外切一次，内切两次．双击按钮“第（3）题”，再分别双击按钮“DE 为腰”和“DE 为底边”，可以体验到，△DEF 为等腰三角形．1．先解读背景图，△ABC是等腰三角形，那么第（3）题中符合条件的△DEF也是等腰三角形．2．用含有x的式子表示BD、DE、MN是解答第（2）题的先决条件，注意点E的位置不同，DE、MN表示的形式分两种情况．3．求两圆相切的问题时，先罗列三要素，再列方程，最后检验方程的解的位置是否符合题意．4．第（3）题按照DE为腰和底边两种情况分类讨论，运用典型题目的结论可以帮助我们轻松解题．满分解答（1）如图2，作BH⊥AC，垂足为点H．在Rt△ABH中，AB＝5，cosA＝310 AHAB=，所以AH＝32＝12AC．所以BH垂直平分AC，△ABC为等腰三角形，AB＝CB＝5．因为DE//BC，所以AB ACDB EC=，即53y x=．于是得到53y x=，（0x>）．（2）如图3，图4，因为DE//BC，所以DE AEBC AC=，MN ANBC AC=，即|3|53DE x-=，1|3|253xMN-=．因此5|3|3xDE-=，圆心距5|6|6xMN-=．图2 图3 图4 在⊙M中，115226Mr BD y x===，在⊙N中，1122Nr CE x==．①当两圆外切时，5162x x +5|6|6x -=．解得3013x =或者10x =-． 如图5，符合题意的解为3013x =，此时5(3)15313x DE -==． ②当两圆内切时，5162x x -5|6|6x -=． 当x ＜6时，解得307x =，如图6，此时E 在CA 的延长线上，5(3)1537x DE -==； 当x ＞6时，解得10x =，如图7，此时E 在CA 的延长线上，5(3)3533x DE -==．图5 图6 图7（3）因为△ABC 是等腰三角形，因此当△ABC 与△DEF 相似时，△DEF 也是等腰三角形．如图8，当D 、E 、F 为△ABC 的三边的中点时，DE 为等腰三角形DEF 的腰，符合题意，此时BF ＝2.5．根据对称性，当F 在BC 边上的高的垂足时，也符合题意，此时BF ＝4.1．如图9，当DE 为等腰三角形DEF 的底边时，四边形DECF 是平行四边形，此时12534BF =．图8 图9 图10 图11考点伸展第（3）题的情景是一道典型题，如图10，如图11，AH 是△ABC 的高，D 、E 、F 为△ABC 的三边的中点，那么四边形DEHF 是等腰梯形．例 7如图1，在直角坐标系xOy 中，设点A （0，t ），点Q （t ，b ）．平移二次函数2tx y -=的图象，得到的抛物线F 满足两个条件：①顶点为Q ；②与x 轴相交于B 、C 两点（∣OB ∣<∣OC ∣），连结A ，B ．（1）是否存在这样的抛物线F ，使得OC OB OA ⋅=2？请你作出判断，并说明理由；（2）如果AQ ∥BC ，且tan ∠ABO ＝23，求抛物线F 对应的二次函数的解析式．图1动感体验请打开几何画板文件名“08杭州24”，拖动点A 在y 轴上运动，可以体验到，AQ 与BC 保持平行，OA ∶OB 与OA ∶OB ′保持3∶2．双击按钮“t ＝3”，“t ＝0．6”，“t ＝－0．6”，“t ＝－3”，抛物线正好经过点B （或B ′）．思路点拨1．数形结合思想，把OC OB OA ⋅=2转化为212t x x =⋅．2．如果AQ ∥BC ，那么以OA 、AQ 为邻边的矩形是正方形，数形结合得到t ＝b ． 3．分类讨论tan ∠ABO ＝23，按照A 、B 、C 的位置关系分为四种情况．A 在y 轴正半轴时，分为B 、C 在y 轴同侧和两侧两种情况；A 在y 轴负半轴时，分为B 、C 在y 轴同侧和两侧两种情况．满分解答（1）因为平移2tx y -=的图象得到的抛物线F 的顶点为Q （t ，b ），所以抛物线F 对应的解析式为b t x t y +--=2)(．因为抛物线与x 轴有两个交点，因此0>b t ．令0=y ，得-=t OB t b，+=t OC tb ． 所以-=⋅t OC OB (|||||tb)( +t t b)|-=2|t 22|OA t tb ==．即22bt t t-=±．所以当32t b =时，存在抛物线F 使得||||||2OC OB OA ⋅=． （2）因为AQ //BC ，所以t ＝b ，于是抛物线F 为t t x t y +--=2)(．解得1,121+=-=t x t x ．①当0>t 时，由||||OC OB <，得)0,1(-t B ．如图2，当01>-t 时，由=∠ABO tan 23=||||OB OA =1-t t ，解得3=t ．此时二次函数的解析式为241832-+-=x x y ．如图3，当01<-t 时，由=∠ABO tan 23=||||OB OA =1+-t t ，解得=t 53．此时二次函数的解析式为-=y 532x ＋2518x ＋12548．图2 图3②如图4，如图5，当0<t 时，由||||OC OB <，将t -代t ,可得=t 53-，3-=t ．此时二次函数的解析式为=y 532x ＋2518x －12548或241832++=x x y ．图4 图5考点伸展第（2）题还可以这样分类讨论：因为AQ //BC ，所以t ＝b ，于是抛物线F 为2()y t x t t =--+．由3tan 2OA ABO OB ∠==，得23OB OA =． ①把2(,0)3B t 代入2()y t x t t =--+，得3t =±（如图2，图5）． ②把2(,0)3B t -代入2()y t x t t =--+，得35t =±（如图3，图4）．2013中考数学压轴题函数等腰三角形问题(一) 例1如图1，已知正方形OABC的边长为2，顶点A、C分别在x、y轴的正半轴上，M 是BC的中点．P(0,m)是线段OC上一动点（C点除外），直线PM交AB的延长线于点D．（1）求点D的坐标（用含m的代数式表示）；（2）当△APD是等腰三角形时，求m的值；（3）设过P、M、B三点的抛物线与x轴正半轴交于点E，过点O作直线ME的垂线，垂足为H（如图2）．当点P从O向C运动时，点H也随之运动．请直接写出点H 所经过的路长（不必写解答过程）．图1 图2动感体验请打开几何画板文件名“11湖州24”，拖动点P在OC上运动，可以体验到，△APD的三个顶点有四次机会可以落在对边的垂直平分线上．双击按钮“第(3)题”，拖动点P由O向C运动，可以体验到，点H在以OM为直径的圆上运动．双击按钮“第(2)题”可以切换．思路点拨1．用含m的代数式表示表示△APD的三边长，为解等腰三角形做好准备．2．探求△APD是等腰三角形，分三种情况列方程求解．3．猜想点H的运动轨迹是一个难题．不变的是直角，会不会找到不变的线段长呢？Rt△OHM的斜边长OM是定值，以OM为直径的圆过点H、C．满分解答（1）因为PC //DB ，所以1CP PM MC BD DM MB ===．因此PM ＝DM ，CP ＝BD ＝2－m ．所以AD ＝4－m ．于是得到点D 的坐标为(2，4－m )．（2）在△APD 中，22(4)AD m =-，224AP m =+，222(2)44(2)PD PM m ==+-． ①当AP ＝AD 时，2(4)m -24m =+．解得32m =（如图3）． ②当PA ＝PD 时，24m +244(2)m =+-．解得43m =（如图4）或4m =（不合题意，舍去）．③当DA ＝DP 时，2(4)m -244(2)m =+-．解得23m =（如图5）或2m =（不合题意，舍去）．综上所述，当△APD 为等腰三角形时，m 的值为32，43或23．图3 图4 图5（3）点H 5． 考点伸展第（2）题解等腰三角形的问题，其中①、②用几何说理的方法，计算更简单： ①如图3，当AP ＝AD 时，AM 垂直平分PD ，那么△PCM ∽△MBA ．所以12PC MB CM BA ==．因此12PC =，32m =．②如图4，当PA ＝PD 时，P 在AD 的垂直平分线上．所以DA ＝2PO ．因此42m m -=．解得43m =． 第（2）题的思路是这样的：如图6，在Rt △OHM 中，斜边OM 为定值，因此以OM 为直径的⊙G 经过点H ，也就是说点H 在圆弧上运动．运动过的圆心角怎么确定呢？如图7，P 与O 重合时，是点H 运动的起点，∠COH ＝45°，∠CGH ＝90°．图6 图7例2如图1，已知一次函数y ＝－x ＋7与正比例函数43y x =的图象交于点A ，且与x 轴交于点B ．（1）求点A 和点B 的坐标；（2）过点A 作AC ⊥y 轴于点C ，过点B 作直线l //y轴．动点P 从点O 出发，以每秒1个单位长的速度，沿O—C —A 的路线向点A 运动；同时直线l 从点B 出发，以相同速度向左平移，在平移过程中，直线l 交x 轴于点R ，交线段BA 或线段AO 于点Q ．当点P 到达点A 时，点P和直线l 都停止运动．在运动过程中，设动点P 运动的时间为t 秒．①当t 为何值时，以A 、P 、R 为顶点的三角形的面积为8？②是否存在以A 、P 、Q 为顶点的三角形是等腰三角形？若存在，求t 的值；若不存在，请说明理由．图1动感体验请打开几何画板文件名“11盐城28”，拖动点R由B向O运动，从图像中可以看到，△APR的面积有一个时刻等于8．观察△APQ，可以体验到，P在OC上时，只存在AP＝AQ的情况；P在CA上时，有三个时刻，△APQ是等腰三角形．思路点拨1．把图1复制若干个，在每一个图形中解决一个问题．2．求△APR的面积等于8，按照点P的位置分两种情况讨论．事实上，P在CA上运动时，高是定值4，最大面积为6，因此不存在面积为8的可能．3．讨论等腰三角形APQ，按照点P的位置分两种情况讨论，点P的每一种位置又要讨论三种情况．满分解答（1）解方程组7, 4,3y xy x=-+⎧⎪⎨=⎪⎩得3,4.xy=⎧⎨=⎩所以点A的坐标是(3，4)．令70y x=-+=，得7x=．所以点B的坐标是(7，0)．（2）①如图2，当P在OC上运动时，0≤t＜4．由8APR ACP PORCORAS S S S=--=△△△梯形，得1113+7)44(4)(7)8222t t t t-⨯-⨯⨯--⨯-=（．整理，得28120t t-+=．解得t＝2或t＝6（舍去）．如图3，当P在CA上运动时，△APR的最大面积为6．因此，当t＝2时，以A、P、R为顶点的三角形的面积为8．图2 图3 图4②我们先讨论P 在OC 上运动时的情形，0≤t ＜4．如图1，在△AOB 中，∠B ＝45°，∠AOB ＞45°，OB ＝7，42AB =，所以OB ＞AB ．因此∠OAB ＞∠AOB ＞∠B ． 如图4，点P 由O 向C 运动的过程中，OP ＝BR ＝RQ ，所以PQ //x 轴．因此∠AQP ＝45°保持不变，∠PAQ 越来越大，所以只存在∠APQ ＝∠AQP 的情况． 此时点A 在PQ 的垂直平分线上，OR ＝2CA ＝6．所以BR ＝1，t ＝1．我们再来讨论P 在CA 上运动时的情形，4≤t ＜7．在△APQ 中， 3cos 5A ∠=为定值，7AP t =-，5520333AQ OA OQ OA OR t =-=-=-． 如图5，当AP ＝AQ 时，解方程520733t t -=-，得418t =． 如图6，当QP ＝QA 时，点Q 在PA 的垂直平分线上，AP ＝2(OR －OP )．解方程72[(7)(4)]t t t -=---，得5t =．如7，当PA ＝PQ 时，那么12cos AQ A AP∠=．因此2cos AQ AP A =⋅∠．解方程52032(7)335t t -=-⨯，得22643t =． 综上所述，t ＝1或418或5或22643时，△APQ 是等腰三角形．图5 图6 图7考点伸展当P 在CA 上，QP ＝QA 时，也可以用2cos AP AQ A =⋅∠来求解．2013中考数学压轴题函数等腰三角形问题(二) 例3如图1，在直角坐标平面内有点A(6, 0)，B(0, 8)，C(－4, 0)，点M、N分别为线段AC和射线AB上的动点，点M以2个单位长度/秒的速度自C向A方向作匀速运动，点N以5个单位长度/秒的速度自A向B方向作匀速运动，MN交OB于点P．(1)求证：MN∶NP为定值；(2)若△BNP与△MNA相似，求CM的长；(3)若△BNP是等腰三角形，求CM的长．图1动感体验请打开几何画板文件名“10闸北25”，拖动点M在CA上运动，可以看到△BNP 与△MNA的形状随M的运动而改变．双击按钮“△BNP∽△MNA”，可以体验到，此刻两个三角形都是直角三角形．分别双击按钮“BP＝BN，N在AB上”、“NB＝NP”和“BP＝BN，N在AB的延长线上”，可以准确显示等腰三角形BNP的三种情况．思路点拨1．第（1）题求证MN∶NP的值要根据点N的位置分两种情况．这个结论为后面的计算提供了方便．2．第（2）题探求相似的两个三角形有一组邻补角，通过说理知道这两个三角形是直角三角形时才可能相似．3．第（3）题探求等腰三角形，要两级（两层）分类，先按照点N 的位置分类，再按照顶角的顶点分类．注意当N 在AB 的延长线上时，钝角等腰三角形只有一种情况．4．探求等腰三角形BNP ，N 在AB 上时，∠B 是确定的，把夹∠B 的两边的长先表示出来，再分类计算．满分解答(1)如图2，图3，作NQ ⊥x 轴，垂足为Q ．设点M 、N 的运动时间为t 秒． 在Rt △ANQ 中，AN ＝5t ，NQ ＝4t ，AQ ＝3t ．在图2中，QO ＝6－3t ，MQ ＝10－5t ，所以MN ∶NP ＝MQ ∶QO ＝5∶3．在图3中，QO ＝3t －6，MQ ＝5t －10，所以MN ∶NP ＝MQ ∶QO ＝5∶3．(2)因为△BNP 与△MNA 有一组邻补角，因此这两个三角形要么是一个锐角三角形和一个钝角三角形，要么是两个直角三角形．只有当这两个三角形都是直角三角形时才可能相似．如图4，△BNP ∽△MNA ，在Rt △AMN 中，35AN AM =，所以531025t t =-．解得3031t =．此时CM 6031=．图2 图3 图4(3)如图5，图6，图7中，OP MP QN MN =，即245OP t =．所以85OP t =． ①当N 在AB 上时，在△BNP 中，∠B 是确定的，885BP t =-，105BN t =-．(Ⅰ)如图5，当BP ＝BN 时，解方程881055t t -=-，得1017t =．此时CM 2017=． (Ⅱ)如图6，当NB ＝NP 时，45BE BN =．解方程()1848105255t t ⎛⎫-=- ⎪⎝⎭，得54t =．此时CM 52=． (Ⅲ)当PB ＝PN 时，1425BN BP =．解方程()1481058255t t ⎛⎫-=- ⎪⎝⎭，得t 的值为负数，因此不存在PB ＝PN 的情况．②如图7，当点N 在线段AB 的延长线上时，∠B 是钝角，只存在BP ＝BN 的可能，此时510BN t =-．解方程885105t t -=-，得3011t =．此时CM 6011=．图5 图6 图7考点伸展如图6，当NB ＝NP 时，△NMA 是等腰三角形，1425BN BP =，这样计算简便一些．例4如图1，在矩形ABCD中，AB＝m（m是大于0的常数），BC＝8，E为线段BC上的动点（不与B、C重合）．连结DE，作EF⊥DE，EF与射线BA交于点F，设CE＝x，BF＝y．（1）求y关于x的函数关系式；（2）若m＝8，求x为何值时，y的值最大，最大值是多少？（3）若12ym，要使△DEF为等腰三角形，m的值应为多少？图1动感体验请打开几何画板文件名“10南通27”，拖动点E在BC上运动，观察y随x变化的函数图像，可以体验到，y是x的二次函数，抛物线的开口向下．对照图形和图像，可以看到，当E是BC的中点时，y取得最大值．双击按钮“m＝8”，拖动E到BC的中点，可以体验到，点F是AB的四等分点．拖动点A可以改变m的值，再拖动图像中标签为“y随x”的点到射线y＝x上，从图形中可以看到，此时△DCE≌△EBF．思路点拨1．证明△DCE∽△EBF，根据相似三角形的对应边成比例可以得到y关于x的函数关系式．2．第（2）题的本质是先代入，再配方求二次函数的最值．3．第（3）题头绪复杂，计算简单，分三段表达．一段是说理，如果△DEF为等腰三角形，那么得到x＝y；一段是计算，化简消去m，得到关于x的一元二次方程，解出x的值；第三段是把前两段结合，代入求出对应的m的值．满分解答(1)因为∠EDC 与∠FEB 都是∠DEC 的余角，所以∠EDC ＝∠FEB ．又因为∠C ＝∠B ＝90°，所以△DCE ∽△EBF ．因此DC EB CE BF =，即8m x x y -=．整理，得y 关于x 的函数关系为218y x x m m =-+． (2)如图2，当m ＝8时，2211(4)288y x x x =-+=--+．因此当x ＝4时，y 取得最大值为2．(3) 若12y m =，那么21218x x m m m=-+．整理，得28120x x -+=．解得x ＝2或x ＝6．要使△DEF 为等腰三角形，只存在ED ＝EF 的情况．因为△DCE ∽△EBF ，所以CE ＝BF ，即x ＝y ．将x ＝y ＝2代入12y m =，得m ＝6（如图3）；将x ＝y ＝6代入12y m =，得m ＝2（如图4）．图2 图3 图4考点伸展本题中蕴涵着一般性与特殊性的辩证关系，例如：由第（1）题得到218y x x m m =-+221116(8)(4)x x x m m m=--=--+， 那么不论m 为何值，当x ＝4时，y 都取得最大值．对应的几何意义是，不论AB 边为多长，当E 是BC 的中点时，BF 都取得最大值．第（2）题m ＝8是第（1）题一般性结论的一个特殊性．再如，不论m 为小于8的任何值，△DEF 都可以成为等腰三角形，这是因为方程218x x x m m=-+总有一个根8x m =-的．第（3）题是这个一般性结论的一个特殊性．2013中考数学压轴题函数相似三角形问题(三)例5已知：如图1，在平面直角坐标系xOy 中，矩形OABC 的边OA 在y 轴的正半轴上，OC 在x 轴的正半轴上，OA ＝2，OC ＝3，过原点O 作∠AOC 的平分线交AB 于点D ，连接DC ，过点D 作DE ⊥DC ，交OA 于点E ．（1）求过点E 、D 、C 的抛物线的解析式；（2）将∠EDC 绕点D 按顺时针方向旋转后，角的一边与y 轴的正半轴交于点F ，另一边与线段OC 交于点G ．如果DF 与（1）中的抛物线交于另一点M ，点M 的横坐标为56，那么EF ＝2GO 是否成立？若成立，请给予证明；若不成立，请说明理由； （3）对于（2）中的点G ，在位于第一象限内的该抛物线上是否存在点Q ，使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形？若存在，请求出点Q 的坐标；若不存在成立，请说明理由．图1动感体验请打开几何画板文件名“09重庆26”，拖动点G 在OC 上运动，可以体验到，△DCG 与△DEF 保持全等，双击按钮“M 的横坐标为1.2”，可以看到，EF ＝2，GO ＝1．拖动点P 在AB 上运动的过程中，可以体验到，存在三个时刻，△PCG 可以成为等腰三角形．。