有理数单元测试题

第一部分有理数单元测试1.下列说法错误的是( )A.零是非负数B.零是整数C.零的相反数是零D.零的倒数是零2.下列说法正确的是( )A.绝对值等于3的数是-3B.绝对值小于113的整数是1和-1C.绝对值最小的有理数是1D.3的绝对值是33.下列判断正确的是( )A.12004的相反数是2004； B.12004的相反数是-2004；C.12004的相反数是-12004； D.12004的相反数是12004-4.下列四组有理数大小的比较正确的是( )A.1123->-；B. 11-->-+;C.1123<;D.1123->-5.有理数a,b,c在数轴上的位置如图所示,下列结论正确的是( )A.b>a>cB.b>-a>cC.a>c>bD.│b│>-a>-c6.数-216不是( )A.有理数B.整数C.负有理数D.自然数7.下列说法正确的是( )A.正整数和负整数统称为整数B.零表示不存在,所以零不是有理数C.非负有理数就是正有理数D.整数和分数统称为有理数8.下列说法错误的个数是( )①一个数的绝对值的相反数一定是负数;②只有负数的绝对值是它的相反数③正数和零的绝对值都等于它本身;④互为相反数的两个数的绝对值相等A.3个B.2个C.1个D.0个9.下列说法正确的是( ).①在+5与-6之间没有正数②在-1与0之间没有负数③在+5与+6之间有无数个正分数④在-1与0之间没有正分数A.仅④正确B.仅③正确C.仅③④正确D.①②④正确10.数a的相反数是-a,那么a表示( )A.负有理数B.正有理数C.正分数D.任意一个数二、填空1.在有理数集合中,最小的正整数是______,最大的负整数是______.2.绝对值最小的有理数是_______.3.相反数最小的负整数是______,相反数最大的正整数是______.4.2.5的相反数是_______,倒数是_____,绝对值是______.5.如果a表示一个有理数,那么-a表示a的______,│a│表示a的_______.6.自行车车轮向顺时针方向旋转200圈记做+200圈, 那么向逆时针方向旋转150圈应记做_________.7. π-的相反数是_____,-a的相反数是________.8.若│y+5│=14,那么y=________.9.在数轴上,离开原点的距离是5的数是__________.10.在数轴上,离开表示数2的点距离是3的点表示的数是_______.三、解答1.写出所有绝对值不大于4的负整数,并在数轴上表示出来.2.若│x-3│+│y+4│+│z-5│=0,求代数式z2-y2+x的值.3.某检修小组乘汽车检修供电线路。

a 10第一章 有理数单元测试一、选择题（每小题4分，共32分）1.下列说法正确的是( ) A.所有的整数都是正数 B.不是正数的数一定是负数C.0不是最小的有理数D.正有理数包括整数和分数 2.12的相反数的绝对值是( ) A.-12 B.2 C.-2 D.12 3.有理数a 、b 在数轴上的位置如图所示,那么下列式子中成立的是( )A.a>bB.a<bC.ab>0D.0a b> 4.在数轴上,原点及原点右边的点表示的数是( )A.正数B.负数C.非正数D.非负数5.下列各组数中,不是互为相反意义的量的是( )A.收入200元与支出20元B.上升10米和下降7米C.超过0.05mm 与不足0.03mD.增大2岁与减少2升6.如果一个数的平方等于它的倒数,那么这个数一定是( )A.0B.1C.-1D.±17.4604608取近似值,保留三个有效数字,结果是( )A.4.60×106B.4600000C.4.61×106D.4.605×1068.下列运算正确的是( ) A.-22÷(-2)2=1 B. 31128327⎛⎫-=- ⎪⎝⎭C.1352535-÷⨯=- D. 133( 3.25)6 3.2532.544⨯--⨯=- 二、填空题(每小题3分，共24分) 9.在数+8.3, 4-,8.0-, 51-, 0, 90, 334-,|24|--中，________________是正数，__________________是负数， 整数.10.某地气温不稳定,开始是6℃,一会儿升高4℃,再过一会儿又下降11℃, 这时气温是__.11.一个数的相反数的倒数是113-,这个数是________.12.数轴上到原点的距离是3个单位长度的点表示的数是______.13.大肠杆菌每过20分便由1个分裂成2个，经过3小时后这种大肠杆菌由1个分裂成__________个.14. 平方等于641 的数是 ，立方等于641 的数是 ，平方等于它本身的数是 .15.绝对值小于5的所有的整数的和_______.16.若│x-1│+(y+2)2=0,则x-y=___________.三、解答题:(共44分)17.计算题(每题5分,共20分)(1)(-12)÷4×(-6)÷2 (2) 235(4)0.25(5)(4)8⎛⎫-⨯--⨯-⨯- ⎪⎝⎭(3) 111311123124244⎛⎫⎛⎫⎛⎫⎛⎫--+----- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ (4) 232121(3)242433⎛⎫⎛⎫-÷⨯-+-⨯- ⎪ ⎪⎝⎭⎝⎭18.(8分)若│a │=2,b=-3,c 是最大的负整数,求a+b-c 的值.19.（8分）检修组乘汽车,沿公路检修线路,约定向东为正,向西为负,某天自A 地出发, 到收工时,行走记录为(单位:千米):+8,-9,+4,+7,-2,-10,+18,-3,+7,+5回答下列问题:(每题5分,共10分)(1)收工时在A 地的哪边?距A 地多少千米?(2)若每千米耗油0.3升,问从A 地出发到收工时,共耗油多少升?20.(8分)某工厂向银行申请了甲种贷款5105.1⨯元，乙种贷款5100.2⨯元，甲种贷款每年的年利率为7%，乙种贷款每年的年利率为6%，问该厂每年付出的利息是多少元？（用科学记数法表示）参考答案一、选择题（每小题4分，共32分）CDADD BAD二、填空题(每小题3分，共24分) 9. +8.3 90, -4 -0.8 -15 -343 -24-, -4 0 90 -24-；10. -1℃； 11. 34； 12. ±3； 13. 512（即29 = 512）； 14. ±18，14，10； 15. 0；16. 3.三、解答题（每小题10分，共30分）17.(1)(-12)÷4×(-6)÷2=(-12)×14×(-6)×12=9. (2)235(4)0.25(5)(4)8⎛⎫-⨯--⨯-⨯- ⎪⎝⎭ =25160.25(4)(5)(4)1080908-⨯-⨯-⨯-⨯-=--=-. (3)111311123124244⎛⎫⎛⎫⎛⎫⎛⎫--+----- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ =111311123124244---++ =1111331111230434422444⎛⎫⎛⎫-++--+=-+=- ⎪ ⎪⎝⎭⎝⎭. (4)232121(3)242433⎛⎫⎛⎫-÷⨯-+-⨯- ⎪ ⎪⎝⎭⎝⎭ =4412744993⎛⎫-⨯⨯+-⨯- ⎪⎝⎭=.1644033-++=.18.∵│a │=2,∴a=±2.c 是最大的负整数,∴c=-1.当a=2时,a+b-c=2-3-(-1)= 0.当a=-2时a+b-c=-2-3-(-1)=-4.19.(1)∵8-9+4+7-2-10+18-3+7+5=8+4+7+18+7+5-9-10-2-3=25,∴在A 处的东边25米处.(2)∵│8│+│-9│+│4│+│7│+│-2│+│-10│+│18│+│-3│+│7│+│5│=73千米,73×0.3=21.9升,∴从出发到收工共耗油21.9升.20. 1.5×510×7%＋2.0×510×6%=2.25×410（元）.。

有理数单元测试题及答案一、选择题（每题2分，共20分）1. 下列哪个数是有理数？A. πB. √2C. 0.33333（无限循环）D. 1/32. 有理数-3和5的和是多少？A. -8B. 2C. -2D. 83. 哪个是有理数的相反数？A. 3B. -3C. 0D. 1/24. 绝对值是5的有理数有几个？A. 1B. 2C. 3D. 45. 下列哪个表达式等于0？A. -3 + 3B. -3 - 5C. -3 × 0D. -3 ÷ 3二、填空题（每题2分，共20分）6. 有理数-7的绝对值是________。

7. 有理数-2和4的差是________。

8. 有理数-6和-3的乘积是________。

9. 有理数-4的倒数是________。

10. 若a是有理数，且a的相反数是-5，则a=________。

三、计算题（每题5分，共30分）11. 计算下列表达式的值：(-3) × (-2) + 4 ÷ (-2)。

12. 解下列方程：3x - 7 = 8。

13. 计算下列各数的绝对值：-12，0，5.5。

14. 求下列数的相反数：-9，3/4，0。

四、解答题（每题10分，共30分）15. 某商店在一天内卖出了价值为-500元的商品（亏损），同时又购入了价值为300元的商品。

请问这一天商店的净亏损是多少？16. 某工厂在一个月内生产了200件产品，每件产品的成本是5元，销售价格是10元。

请问工厂这个月的纯利润是多少？17. 某学生在一次数学测验中得了85分，第二次测验得了90分，第三次测验得了75分。

请问该学生这三次测验的平均分是多少？答案一、选择题1. D2. C3. B4. B5. A二、填空题6. 77. -68. 189. -1/410. 5三、计算题11. 412. x = 513. 12，0，5.514. 9，-3/4，0四、解答题15. 净亏损200元16. 纯利润1000元17. 平均分81.67分（保留两位小数）结束语本测试题旨在检验学生对有理数的基本概念、运算规则和实际应用的理解。

《有理数》单元测试卷基础部分一、选择题（本大题共10小题，共40分）：1、在–1，–2，1，2四个数中，最大的一个数是（ ） （A ）–1 （B ）–2 （C ）1 （D ）22、有理数31的相反数是（ ）（A ）31 （B ）31- （C ）3 （D ） –33、有理数–3的倒数是（ ） （A ）–3 （B ）31-（C ）3 （D ）31 4、计算：（＋1）＋（–2）等于（ ）（A ）–l （B ） 1 （C ）–3 （D ）35、我国拟设计建造的长江三峡电站，估计总装机容量将达16780000千瓦，用科学记数法表示总装机容量是（ ）（A ）4101678⨯千瓦（B ）61078.16⨯千瓦（C ）710678.1⨯千瓦（D ）8101678.0⨯千瓦6、下列说法中,正确的是( )(A)相反数等于它本身的有理数只有0; (B)倒数等于它本身的有理数只有1 (C)绝对值等于它本身的有理数只有0; (D)平方结果等于它本身的有理数只有17、大于–3.5，小于2.5的整数共有（ ）个。

（A ）6 （B ）5 （C ）4 （D ）38、已知数b a ,在数轴上对应的点在原点两侧，并且到原点的位置相等；数y x ,是互为倒数，那么xy b a 2||2-+的值等于（ ） （A ）2 （B ）–2 （C ）1 （D ）–1 9、如果a a =||，那么a 是（ ）（A ）0 （B ）0和1 （C ）正数 （D ）非负数10、如果两个有理数的积是正数，和也是正数，那么这两个有理数（ ） （A ）同号，且均为负数 （B ）异号，且正数的绝对值比负数的绝对值大 （C ）同号，且均为正数 （D ）异号，且负数的绝对值比正数的绝对值大 二、填空题：（本大题共4小题，共20分）11、如果向银行存入人民币20元记作+20元，那么从银行取出人民币32.2元记作________。

12、比较大小：–π________–3.14（填=，＞，＜号＝。

初一数学有理数单元测试题一、选择题（每题2分，共20分）1. 下列哪个数是有理数？A. πB. √2C. 0.33333（无限循环）D. 1/32. 如果a和b是有理数，且a + b = 0，那么a和b的关系是：A. 相等B. 互为相反数C. 互为倒数D. 互为倍数3. 以下哪个表达式的结果不是有理数？A. √4B. 2^3C. √9D. 3.14154. 两个有理数相除，结果为：A. 一定为有理数B. 可能是无理数C. 一定是无理数D. 可能是有理数，也可能是无理数5. 下列哪个数的绝对值最小？A. -5B. 3C. 0D. 7二、填空题（每题2分，共20分）6. 若|a| = 5，且a > 0，则a = _______。

7. 将-23.5转化为分数形式为 _______。

8. 两个数的和为-6，其中一个数为-3，另一个数为 _______。

9. 计算(-7) × (-8) = _______。

10. 若a = -4，b = 2，则a + b = _______。

三、计算题（每题5分，共30分）11. 计算下列各题，并写出计算过程：(1) 3.5 + (-2.1)(2) (-3) × 412. 计算下列各题，并写出计算过程：(1) |-12| - 5(2) (-1)^3 + 2^213. 计算下列各题，并写出计算过程：(1) (-7) ÷ (-2)(2) (-5) × (-3) + 414. 解下列方程，并写出解题过程：(1) 2x + 5 = 11(2) 3y - 7 = 8四、解答题（每题10分，共30分）15. 某商店在一天内卖出了100件商品，每件商品的售价为20元。

如果每件商品的成本为15元，求商店这一天的纯利润。

16. 某工厂计划在一个月内生产500个零件，每个零件的成本为10元，计划每个零件的售价为15元。

如果实际生产了480个零件，并且每个零件的售价为12元，求工厂这个月的纯利润。

有理数单元测试及答案有理数单元检测试题一、填空题（本题共有9个小题，每小题2分，共18分）1、一幢大楼地面上有12层，还有地下室2层，如果把地面上的第一层作为基准，记为0，规定向上为正，那么惯上将2楼记为1；地下第一层记作-1；数-2的实际意义为地下第三层，数+9的实际意义为地面上的第十层。

2、如果数轴上的点A对应有理数为-2，那么与A点相距3个单位长度的点所对应的有理数为-5.3、某数的绝对值是5，那么这个数是-5或5.（保留四个有效数字）4、(4/3)²=16/9，(-4/3)²=16/9.5、数轴上和原点的距离等于3的点表示的有理数是-3或3.6、计算：（-1）+（-1）=-2.7、如果a、b互为倒数，c、d互为相反数，且m=-1，则代数式2ab-（c+d）+m=-1.8、（+5.7）的相反数与（-7.1）的绝对值的和是12.8.9、已知每辆汽车要装4个轮胎，则51只轮胎至多能装配12辆汽车。

二、选择题（本题共有10个小题，每小题都有A、B、C、D四个选项，请你把你认为适当的选项前的代号填入题后的括号中，每题2分，共20分）10、下列说法正确的是（C）。

A。

整数就是正整数和负整数B。

负整数的相反数就是非负整数C。

有理数中不是负数就是正数D。

零是自然数，但不是正整数11、下列各对数中，数值相等的是（A）。

A。

-2与(-2)B。

-3与(-3)C。

-3×2与-3×2D。

-( -3)与-( -2)12、在-5，-9，-3.5，-0.01，-2，-212各数中，最大的数是（D）。

A。

-12B。

-9C。

-0.01D。

-213、如果一个数的平方与这个数的差等于1，那么这个数只能是（B）。

A。

-1B。

1C。

0D。

或114、绝对值大于或等于1，而小于4的所有的正整数的和是（C）。

A。

8B。

7C。

6D。

515、计算：(-2)+(-2)的是（D）。

A。

2B。

-1C。

-2D。

有理数单元测试题及答案一、选择题（每题2分，共10分）1. 下列哪个数是有理数？A. πB. √2C. 1/3D. 0.33333（无限循环）答案：C2. 如果a和b都是有理数，且a > b，那么下列哪个选项是正确的？A. a + b > 0B. a - b > 0C. a × b > 0D. a ÷ b > 0答案：B3. 两个负有理数相加的结果是什么？A. 正数B. 负数C. 零D. 无法确定答案：B4. 下列哪个数是无理数？A. 0.5B. √3C. 1/7D. 3.1415答案：B5. 有理数a和b的绝对值相等，且a < b，那么a和b的和是多少？A. aB. bC. 0D. -2a答案：D二、填空题（每题2分，共10分）6. 如果一个有理数的绝对值是5，那么这个数可以是______或______。

答案：5，-57. 两个有理数相除，如果商是正数，那么这两个数的符号必须______。

答案：相同8. 如果一个有理数的平方是9，那么这个数可以是______或______。

答案：3，-39. 有理数的加法运算满足交换律，即a + b = ______ + a。

答案：b10. 有理数的乘法运算满足结合律，即(a × b) × c = a ×(______ × c)。

答案：b三、计算题（每题5分，共15分）11. 计算下列表达式的值：(-3) × 2 + 4 × (-2) - 6。

答案：原式 = -6 - 8 - 6 = -2012. 计算下列表达式的值：(-4)² - 3 × 2 - 5。

答案：原式 = 16 - 6 - 5 = 513. 计算下列表达式的值：(-2)³ + 3 × (-1/3) - 1。

答案：原式 = -8 - 1 - 1 = -10四、解答题（每题10分，共20分）14. 某商店在一天内卖出了10件商品，每件商品的售价为x元，成本为y元。

有理单元测试题及答案一、选择题1. 下列哪个数是有理数？A. πB. √2C. 3.14D. 0.3333...答案：C2. 如果一个数的绝对值是5，那么这个数可能是：A. 5B. -5C. 5或-5D. 都不是答案：C3. 以下哪个运算结果不是有理数？A. 2 + 3B. 4 - 6C. √4D. 2 / 3答案：B二、填空题4. 如果一个数的相反数是-7，那么这个数是________。

答案：75. 绝对值不大于5的所有整数有：-5，-4，-3，-2，-1，0，1，2，3，4，5。

三、简答题6. 请解释什么是有理数，并给出两个例子。

答案：有理数是可以表示为两个整数的比的数，即形式为a/b，其中a和b都是整数，且b≠0。

例如，1/2和3都是有理数。

7. 请解释绝对值的概念，并给出一个绝对值的例子。

答案：绝对值是一个数去掉其符号后的值，表示该数到数轴原点的距离。

例如，|-5|的绝对值是5。

四、计算题8. 计算下列表达式的值：(1) |-7|(2) 3 + (-2)(3) (-1) × 5答案：(1) 7(2) 1(3) -5五、解答题9. 某商店在一天内卖出了价值为-100元的商品（亏损），又卖出了价值为150元的商品（盈利）。

请问该商店当天的总盈利或亏损是多少？答案：该商店当天的总盈利为150 - 100 = 50元。

结束语：通过本单元测试题，我们复习了有理数的基本概念、性质以及相关的运算。

希望同学们能够通过练习加深对有理数的理解，并在实际问题中灵活运用。

有理数单元测试题一、选择题（本大题共10小题，共30分） 1.下列各数表示准确数的是()A. 小明同学买了6支铅笔B. 小亮同学的身高是1.72mC. 教室的面积是60m2D. 小兰在菜市场买了3斤西红柿1.下列说法：①近似数3.45精确到百分位；②近似数0.50精确到百分位，③2019.5精确到个位是2019.其中说法正确的个数有()A. 1个B. 2个C. 3个D. 0个2.关于(−3)4的正确说法是()A. −3是底数，4是幂B. −3是底数，4是指数，−12是幂C. 3是底数，4是指数，81是幂D. −3是底数，4是指数，81是幂3.在算式|5□(−3)|+4中的□所在位置，填入下列哪种运算符号，计算出来的值最大()A. +B. −C. ×D. ÷4.已知xy>0，x+y<0，则()A. x>0，y>0B. x<0，y<0C. x>0，y<0D. x<0，y>05.若a+b<0，ba>0，则下列结论成立的是()A. a>0，b>0B. a<0，b<0C. a>0，b<0D. a<0，b>06.计算1357×316最简便的方法是()A. (13+57)×316B. (14−27)×316C. (10+357)×316D. (16−227)×3167.计算(−1)2017−(−1)2018等于()A. 0B. 2C. −2D. −18.用科学记数法表示136000，其结果是()A. 0.136×106B. 1.36×105C. 136×103D. 136×1069.有理数a、b在数轴上的对应位置如图所示，则a+b的值为()A. 正数B. 负数C. 0D. 非正数二、填空题（本大题共10小题，共30分）10.四舍五入求近似值：0.7951≈__________ (精确到0.01)11.已知2.73×10n是一个7位数，则n=________，原数为________．12.已知a，b互为相反数，c，d互为倒数，m的绝对值等于2.则a+ba+b+c−2cd+m=0的值为________．13.若｜m｜=7，｜n｜=4，那么mn=________．14.计算：(−22)×57×(−311)×(−21)=______．15.计算：1+(−2)+3+(−4)+5+(−6)+⋯+99+(−100)=______．16.已知两个数的和为−225，其中一个数为−134，则另一个数是________．17.已知|x|=7，|y|=2，且x<y，则x−y的值为________．18.若a是−[−(−7)]的相反数，则a=________．19.如果2a−5与−7互为相反数，则a=________．三、计算题21、（本大题共1小题，共6×4=24分）(1)(−1)100×5+(−2)4÷4；(2)(−3)3−3×(−13)4；(3)76×(16−13)×314÷35；(4)(−10)3+[(−4)2−(1−32)×2]；(5)−23÷49×(−23)2；(6)4+(−2)3×5−(−0.28)÷4．四、解答题（本大题共6小题，共36分）20.已知数轴上有点A，B，A，B两点之间的距离是1个单位长度，点A到原点O的距离是3个单位长度，那么点B对应的数可能是多少?（5分）21.在活动课上，有6名学生用橡皮泥做了6个乒乓球，直径可以有0.02毫米的误差，超过规定直径的毫米数记作正数，不足的记为负数，检查结果如下表：(1)请你指出哪些同学做的乒乓球是合乎要求的？(2)指出合乎要求的乒乓球中哪个同学做的质量最好？哪个同学做的质量较差？(3)请你对6名同学做的乒乓球质量按照最好到最差排名；(4)用学过的绝对值知识来说明以上问题．（1+2+2+1=6分）22.已知a=−212，b=−314，c=413，求下列各式的值．（3+3=6分）(1)a−b+c；(2)a−b−c．23.已知a、b互为相反数，c、d互为倒数，m是绝对值等于2的数，求：a+ba+b+c+m2−cd 的值．（5分）24.观察下面三行数．（2+2+3=7分）−2，4，−8，16，−32，64，…；−4，2，−10，14，−34，62，…；4，−8，16，−32，64，−128，…．(1)第一行数按什么规律排列？(2)第二行、第三行和第一行分别有什么关系？(3)取每行的第100个数，计算这三个数的和．25.观察下列等式：（4+3=7分）第1个等式：a1=11×3=12×(1−13)；第2个等式：a2=13×5=12×(13−15)；第3个等式：a3=15×7=12×(15−17)；第4个等式：a4=17×9=12×(17−19)；……请解答下列问题：(1)按以上规律列出第5个等式：a5=________=________；(2)用含n的式子表示第n个等式：a n=____________=____________(n为正整数)；(3)求a1+a2+a3+a4+⋯+a100的值．有理数测试题答案【答案】1. A2. B3. D4. C5. B6. B7. D8. C9. B10. A11. 0.8012. 6；273000013. 0或−414. ±2815. −9016. −5017. −132018. −9或−519. 720. 621. 解：(1)原式=1×5+16÷4=5+4=9；(2)原式=−27−3×181=−27−1 27=−27127；(3)原式=76×(−16)×314×53=−572；(4)原式=−1000+[16−(−8)×2]=−1000+(16+16)=−1000+16+16 =−968；(5)原式=−8×94×49=−8；(6)原式=4+(−8)×5+0.07=4−40+0.07 =−35.93．22. 解：当点A 表示3时，点B 表示的数是2或4，当点A 表示−3时，点B 表示的数是−2或−4．23. 解：(1)∵绝对值小于0.02的数有−0.017，−0.011，∴张兵、蔡伟做的乒乓球是合乎要求的； (2)∵|−0.011|<|−0.017|，∴蔡伟做的质量最好，张兵做的质量较差；(3)∵|−0.011|<|−0.017|<|−0.021|<|+0.022|<|+0.023|<|+0.031|， ∴从最好到最差排名为：蔡伟、张兵、余佳、赵平、王敏、李明； (4)这是绝对值在实际生活中的应用，对误差来说绝对值越小越好．24. 解：(1)原式=(−212)−(−314)+413=−52+134+133=−30+39+5212=6112；(2)原式=(−212)−(−314)−413=−52+134−133=−30+39−5212=−4312．25. 解：∵a 、b 互为相反数，c 、d 互为倒数，m 是绝对值等于2的数，∴a +b =0，cd =1，m 2=4， ∴a+ba+b+c +m 2−cd =0+4−1=3．26. 解：(1)第一行数的规律是：从第一个数开始，后面一个数是前面一个数乘−2得到的，即−2，(−2)2，(−2)3，(−2)4……， 则第n 个数为(−2)n ；(2)第一行数−2对应得出第二行的数，即(−2)n −2； 第一行数×(−2)对应得出第三行的数，即(−2)n+1； (3)∵第一行的第100个数为(−2)100， 第二行的第100个数为(−2)100−2，；第三行的第100个数为(−2)100×(−2)=(−2)101(−2)100+[(−2)100−2]+(−2)101=(−2)100+(−2)100+(−2)101−2 =(−2)100(1+1−2)−2=−2．27. 解：(1)19×11 12×(19−111)；1×(12n−1−12n+1)；(3)a1+a2+a3+a4+⋯+a100=12×(1−13)+12×(13−15)+12×(15−17)+12×(17−19)+···+12×(1199−1201) =12×(1−13+13−15+15−17+17−19+···+1199−1201)=1×(1−1)=12×200201=100201．。

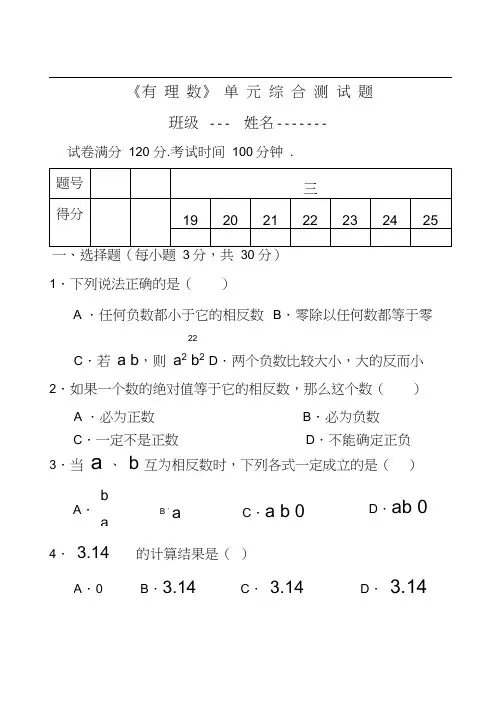
《有 理 数》 单 元 综 合 测 试 题班级 --- 姓名 -------试卷满分 120 分.考试时间 100分钟 .一、选择题（每小题 3分，共 30 分）1．下列说法正确的是（）A ．任何负数都小于它的相反数B ．零除以任何数都等于零22C ．若 a b ，则 a 2 b 2D ．两个负数比较大小，大的反而小 2．如果一个数的绝对值等于它的相反数，那么这个数（）A ．必为正数B ．必为负数 3．当a 、b 互为相反数时，下列各式一定成立的是（）4． 3.14 的计算结果是（ ）C ．一定不是正数D ．不能确定正负b A ．aB ．aC ．a b 0D ．ab 0A ．0B ．3.14C ． 3.14D ． 3.145．a 为有理数，则下列各式成立的是(A．a2 0 B．1 a2 0C．( a) 0 D．a2 1 06．如果一个数的平方与这个数的绝对值相等，那么这个数是 () A．0 B．1 C．-1 D．0，1或-1 7．若 3.0860 是四舍五入得到的近似数，则下列说法中正确的是( )A．它精确到0.00001B．它精确到万分位C．它精确到0.001D．它精确到千分位8．已知a0，1 b 0，则a ，ab ，ab2按从小到大的顺序排列为( )A．a ab ab2B．ab2a ab C．a b a b2a D ．a ab2ab 9. 下列各组运算中，其值最小的是( )A．( 3 2)2B．( 3) ( 2)C．( 3)2 ( 2)2D．( 3)2 ( 2)10. 几个同学在日历纵列上圈出了三个数，算出它们的和，其中错误的一个是（）A ．28 B．33 C．45 D．57二、填空题（每小题3分，共24 分）11．绝对值小于 5 的整数共有______________________________ 个。

12．当a b 0时，1__________ 1（填“>”“ =”或“<”）。