当前位置：文档之家 › 武汉理工材料力学第07章a(应力状态)

武汉理工材料力学第07章a(应力状态)

  • 格式：ppt
  • 大小：5.43 MB
  • 文档页数：95

下载文档原格式

  / 95

合集下载

材料力学习题册答案_第7章_应力状态

材料力学习题册答案_第7章_应力状态

第 七 章 应力状态 强度理论一、 判断题1、平面应力状态即二向应力状态，空间应力状态即三向应力状态。

(√)2、单元体中正应力为最大值的截面上，剪应力必定为零。

(√)3、单元体中剪应力为最大值的截面上，正应力必定为零。

(×) 原因：正应力一般不为零。

4、单向应力状态的应力圆和三向均匀拉伸或压缩应力状态的应力圆相同，且均为应力轴 上的一个点。

(×) 原因：单向应力状态的应力圆不为一个点，而是一个圆。

三向等拉或等压倒是为一个点。

5、纯剪应力状态的单元体，最大正应力和最大剪应力值相等，且作用在同一平面上。

(×) 原因：最大正应力和最大剪应力值相等，但不在同一平面上6、材料在静载作用下的失效形式主要有断裂和屈服两种。

(√)7、砖,石等脆性材料式样压缩时沿横截面断裂。

(×)8、塑性材料制成的杆件，其危险点必须用第三或第四强度理论所建立的强度条件来校核强度。

(×) 原因：塑性材料也会表现出脆性，比如三向受拉时，此时，就应用第一强度理论9、纯剪应力状态的单元体既在体积改变，又有形状改变。

(×) 原因：只形状改变，体积不变10、铸铁水管冬天结冰时会因冰膨胀被胀裂，而管的冰不会被破坏，只是因为冰的强度比铸铁的强度高。

(×) 原因：铸铁的强度显然高于冰，其破坏原因是受到复杂应力状态二、 选择题1、危险截面是（ C ）所在的截面。

A 最大面积B 最小面积C 最大应力D 最大力2、关于用单元体表示一点处的应力状态，如下论述中正确的一种是( D )。

A 单元体的形状可以是任意的B 单元体的形状不是任意的，只能是六面体微元C 不一定是六面体，五面体也可以，其他形状则不行D 单元体的形状可以是任意的，但其上已知的应力分量足以确定任意方向面上的硬力 3、受力构件任意一点，随着所截取截面方位不同，一般来说（ D ） A 正应力相同，剪应力不同 B 正应力不同，剪应力相同 C 正应力和剪应力均相同 D 正应力和剪应力均不同 4、圆轴受扭时，轴表面各点处于（ B ）A 单向应力状态B 二向应力状态C 三向应力状态D 各向等应力状态 5、分析处于平面应力状态的一点，说确的是（ B ）。

工程力学c材料力学部分第七章 应力状态和强度理论

工程力学c材料力学部分第七章 应力状态和强度理论

无论是强度分析还是刚度分析，都需要求出应力的极值， 无论是强度分析还是刚度分析，都需要求出应力的极值，为了找 到构件内最大应力的位置和方向 需要对各点的应力情况做出分析。 最大应力的位置和方向， 到构件内最大应力的位置和方向，需要对各点的应力情况做出分析。
受力构件内一点处所有方位截面上应力的集合，称为一点的 受力构件内一点处所有方位截面上应力的集合，称为一点的 研究一点的应力状态时， 应力状态 。研究一点的应力状态时，往往围绕该点取一个无限小 的正六面体—单元体来研究。 单元体来研究 的正六面体 单元体来研究。
σ2
σ2
σ1
σ1
σ
σ
σ3
三向应力状态
双向应力状态
单向应力状态 简单应力状态
复杂应力状态 主应力符号按代数值的大小规定： 主应力符号按代数值的大小规定：
σ1 ≥ σ 2 ≥ σ 3
平面应力状态的应力分析—解析法 §7−2 平面应力状态的应力分析 解析法
图(a)所示平面应力单元体常用平面图形(b)来表示。现欲求 )所示平面应力单元体常用平面图形( )来表示。现欲求 垂直于平面xy的任意斜截面 上的应力 垂直于平面 的任意斜截面ef上的应力。 的任意斜截面 上的应力。
二、最大正应力和最大剪应力
σα =
σ x +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
τα =
令
σ x −σ y
2
sin 2α + τ x cos 2α
dσ α =0 dα
σ x −σ y
2
sin 2α +τ x cos2α = 0
可见在 τ α
=0

武汉理工大学材料力学课件7 应力状态和强度理论

武汉理工大学材料力学课件7 应力状态和强度理论
2

x y
2 2 3 3 x x 120 MPa (1) 4 2 x y sin 2 x cos 2 2
30
2

x y
2
cos 2 x sin 2
x y sin 2 x cos 2 2


x y
2 x y 2

x y
2
cos 2 x sin 2
sin 2 x cos 2
二、主平面和主应力 x y 令 ＝ 0 时， ＝ 0＝ sin 2 0 x cos 2 0 0 2 2 x tan2 0 x y
y
c

1、 与截面外法线同向为正； 2、 对研究对象内任一点的矩为顺时针转向时为正； 3、 由x逆时针转向截面外法线为正。
设：斜截面面积为dA，由分离体平衡得：
a

b
x

n

F
n
0: dA x dA cos2 x dA cos sin
x
y
4
低碳钢
铸铁
塑性材料拉伸时为什么会出现滑移线？
5
低碳钢
铸铁
为什么脆性材料扭转时沿45º 螺旋面断开？6
二、一点处的应力状态： 受力构件内一点处不同方位截面上的应力的集合。 三、研究方法： 取单元体的方法。 单元体：围绕受力构件内任意点切取的微元体。
dz
dy
单 元 体 的 特 点
dx dy dz 0
xy
1
x y x y 2 2 主 （ ） x 2 2 1 2 0 3
2 x tan2 0 x y 0 45

材料力学第七章知识点总结

材料力学第七章知识点总结

p
σα
α
τα
)
(−
B
各边边长,
d x d y
σ
x
σ
y σ
z
τ
xy
τ
yx
τ
yz
τ
zy
τ
zx
τ
xz
（2) 应力状态的分类
a、单向应力状态：只有一个主应力不等于零，另两个主应力
都等于零的应力状态。

b、二向应力状态：有两个主应力不等于零，另一个主应力
等于零的应力状态。

c、三向应力状态：三向主应力都不等于零的应力状态。

平面应力状态：单向应力状态和二向应力状态的总称。

空间应力状态：三向应力状态
简单应力状态：单向应力状态。

复杂应力状态：二向应力状态和三向应力状态的总称。

纯剪切应力状态：单元体上只存在剪应力无正应力。

y
x
σx
σy
σz
τxy τyx
τyz
τzy τzx
τxz
x
y
σx
σy
τyx
τxy
τ第一个下标表示微面元方向,第二个下标表示面元上力的方向
空间问题简化
为平面问题
α——由o
c
b
σττ
σ
ττ
τ
max τ
min
τα
D
A
H
3040MPa
7.27422
)
7.27(=−−
σ
x
σ
y σ
z
τ
xy
τ
yx
τ
yz
τ
zy
τ
zx
τ
xz
y
x
z。

武汉理工大学材料力学7-8-9zhang

武汉理工大学材料力学7-8-9zhang

yx
b、平行面上，应力相等。
x、 y、 z、 xy、 yx、 yz、 zy、 zx、 xz
xy xy yx
切应力互等定理:
在单元体相互垂直的两个平面上，切应力必然 成对出现，且数值相等，两者都垂直于两平面的交 线，其方向则共同指向或共同背离该交线。
yx
xy yx, xz zx ,
§7－2 二向应力状态分析
平面应力状态： 单元体上有一组面上的应力分量都为零。一
般取应力分量为零的面的外法线为z。这时有：
z zy zx 0， x 0， y 0， xy 0
Ⅰ. 斜截面上的应力
现先分析与已知应力所在平面xy垂直的任意斜截面 (图b)上的应力。
1、 与截面外法线同向为正； 2、τa 绕研究对象顺时针转动为正； 3、α由x逆时针转向截面外法线为正。
1）主平面(Principal Plane)： 切应力为零的方向面。
2） 主应力(Principal Stress ）： 主平面上的正应力。
3）主单元体(Principal Element)： 各侧面上切应力均为零的单元体。
x A x 4）主应力排列：按代数值大小，
1 2 3
5）三向应力状态（ state of triaxial
n
x
2
y
sin 2
xy
cos 2
Ⅱ 二向应力状态下主单元体、主平面、主应力的确定
令
x
y
2
sin 2
xy
cos 2
0
得：tan
20
2 xy x
y
即-900 20 900时，0 0
*共有三个主平面(即切应力为零的方向面），分别是：
1） =0的方向面为一个主平面；

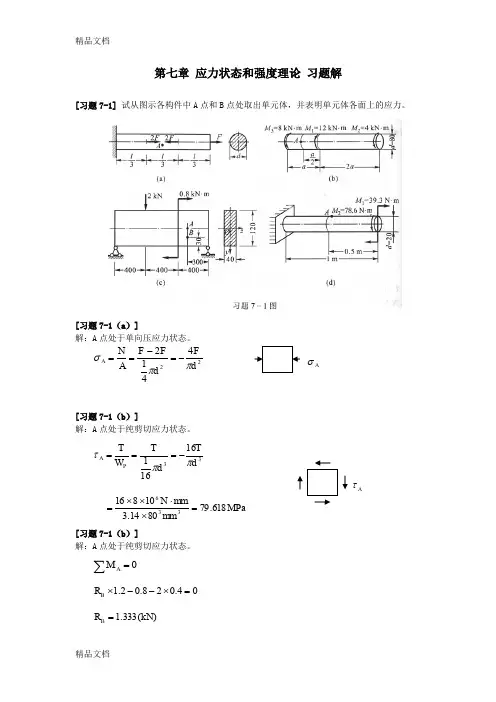
《材料力学》第7章-应力状态和强度理论-习题解讲课教案

《材料力学》第7章-应力状态和强度理论-习题解讲课教案

第七章 应力状态和强度理论 习题解[习题7-1] 试从图示各构件中A 点和B 点处取出单元体，并表明单元体各面上的应力。

[习题7-1（a ）]解：A 点处于单向压应力状态。

224412d F d F F A N A ππσ-=-==[习题7-1（b ）]解：A 点处于纯剪切应力状态。

3316161d T d T W T P A ππτ-===MPa mm mm N 618.798014.310816336=⨯⋅⨯⨯=[习题7-1（b ）]解：A 点处于纯剪切应力状态。

0=∑AM04.028.02.1=⨯--⨯B R )(333.1kN R B =)(333.1kN R Q B A -=-=MPa mmN A Q A 417.01204013335.15.12-=⨯⨯-=⨯=τB 点处于平面应力状态MPamm mm mm N I y M zB B 083.21204012130103.0333.1436=⨯⨯⨯⋅⨯⨯==σMPa mm mm mmN b I QS z zB 312.0401204012145)3040(1333433*-=⨯⨯⨯⨯⨯⨯-==τ[习题7-1（d ）]解：A 点处于平面应力状态MPa mm mm N W M zA A 064.502014.3321103.39333=⨯⨯⋅⨯==σMPa mm mm N W T PA 064.502014.3161106.78333=⨯⨯⋅⨯==τ [习题7-2] 有一拉伸试样，横截面为mm mm 540⨯的矩形。

在与轴线成045=α角的面上切应力MPa 150=τ时，试样上将出现滑移线。

试求试样所受的轴向拉力F 。

解：AFx =σ；0=y σ；0=x τ 004590cos 90sin 20x yx τσστ+-=A F 2045=τ 出现滑移线，即进入屈服阶段，此时，1502045≤=AFτ kN N mm mm N A F 6060000540/30030022==⨯⨯==[习题7-3] 一拉杆由两段沿n m -面胶合而成。

材料力学(机械工业出版社)知识小结：第七章 应力状态与应变状态分析

材料力学(机械工业出版社)知识小结：第七章 应力状态与应变状态分析

第七章应力状态与应变状态分析7–１应力状态的概念一、一点的应力状态：过受力构件内一点有无数的截面，这一点的各个截面上应力情况的集合，称为这点的应力状态二、为什么要研究应力状态？三、怎样研究应力状态单元体：单元体——构件内的点的代表物，是包围被研究点的无限小的几何体，常用的是正六面体。

单元体的性质——a 、每个平面上，应力均布； b 、平行面上，应力相等。

四、普遍状态下的应力表示（图略6）五、剪应力互等定理过一点的两个正交面上,如果有与相交边垂直的剪应力分量,则两个面上的这两个剪应力分量一定等值、方向相对或相离。

yx xy ττ=六、原始单元体（已知单元体）：七、主单元体、主平面、主应力1、主单元体：各侧面上剪应力均为零的单元体。

2、主平面：剪应力为零的截面。

3、主应力：主平面上的正应力。

4、主应力排列规定：按代数值大小，321σσσ≥≥5、三向应力状态：三个主应力都不为零的应力状态。

6、二向应力状态：一个主应力为零的应力状态。

7、单向应力状态：一个主应力不为零的应力状态。

7–2平面应力状态分析——解析法一、任意斜截面上的应力规定：1、σα截面外法线同向为正；2、t a 绕研究对象顺时针转为正；3、a 逆时针为正。

ατασσσσσα2sin 2cos 22xy y x y x --++= ατασστα2cos 2sin 2xy yx +-=二、极值应力yx xyσστα--=22tg 0 和两个极值：）、（20101παα+⎪⎩⎪⎨⎧+-±+=22minmax )2(2xy y x y x τσσσσσσ⎪⎩⎪⎨⎧+-±=22minmax )2(xy y x τσσττ7–3平面应力状态分析——图解法一、应力圆⎪⎪⎩⎪⎪⎨⎧+-=--++=ατασστατασσσσσαα2cos 2sin 22sin 2cos 22xy y x xy y x y x 对上述方程消去参数（2α），得：222222xy y x y x τσστσσσαα+⎪⎪⎭⎫ ⎝⎛-=+⎪⎪⎭⎫ ⎝⎛+-，此方程曲线为圆—应力圆 二、应力圆的画法1、建立应力坐标系，如下图所示，（注意选好比例尺）2、在坐标系内画出点A (σx ，τxy )和B (σy ，τyx )3、AB 与σa 轴的交点C 便是圆心4、以C 为圆心，以AC 为半径画圆——应力圆三、单元体与应力圆的对应关系1、α面上的应力(σα，τα)→应力圆上一点(σα，τα)2、α面的法线→应力圆的半径3、两面夹角α→两半径夹角2α；且转向一致。

材料力学-7-应力状态分析

材料力学-7-应力状态分析

7.1 应力状态的基本概念
y
y
1 1 4
z
4
Mz
x
x
l
S FP
2
3
Mx
z
3
a
第7章 应力状态分析
7.2 平面应力状态任意方向面上的应力 ——解析法
7.2 平面应力状态任意方向面上的应力 ——解析法
一、方向角与应力分量的正负号约定
x
正应力
x
x
拉为正
压为负
x
7.2 平面应力状态任意方向面上的应力 ——解析法
？
第7章 应力状态分析 7.1 应力状态的基本概念
7.2 平面应力状态任意方向面上的应力 ——解析法 7.3 主应力、主平面与面内最大切应力 ——解析法 7.4 应力圆及其应用——图解法
7.5 三向应力状态的特例分析
7.6 广义胡克定律
7.7 应变能密度
第7章 应力状态分析
tan 2q p＝－ 2 τ
xy
x y
主平面（principal plane）：切应力q＝0的方向面，用 qp表示。 主应力（principal stress）：主平面上的正应力。 主方向（principal directions）：主平面法线方向，用方 向角qp表示。
7.3 主应力、主平面与面内最大切应力 ——解析法
第7章 应力状态分析
第7章 应力状态分析
1
3
2
max
max
拉压、弯曲正应力 扭转、弯曲切应力
这些强度问题的共同特点是：
1、危险截面上的危险点只承受正应力 或切应力； 2、都是通过实验直接确定失效时的极限应力，并以此为依据建立强度 设计准则。 复杂受力：危险截面上危险点同时承受正 应力和切应力，或者危险点的其他面上同 时承受正应力或切应力。 → 强度条件

《材料力学》第7章-应力状态和强度理论-习题解

《材料力学》第7章-应力状态和强度理论-习题解
解：左支座为A，右支座为B，左集中力作用点为C，右集中力作用点为D。
支座反力: (↑)
=
（1）梁内最大正应力发生在跨中截面的上、下边缘
超过 的5。3％，在工程上是允许的。
（2）梁内最大剪应力发生在支承截面的中性轴处
(3)在集中力作用处偏外侧横截面上校核点a的强度
超过 的3.53%，在工程上是允许的。
解：坐标面应力:X（—0。05，0);Y（-0.2,0）
。根据以上数据作出如图所示的应
力圆。图中比例尺为 代表 。
按比例尺量得斜面的应力为：
按习题7—5得到的公式计算如下：
作图法(应力圆法)与解析法（公式法）的结果一致。
［习题7-7]试用应力圆的几何关系求图示悬臂梁距离自由端为 的截面上，在顶面以下 的一点处的最大及最小主应力,并求最大主应力与 轴之间的夹角。
解：
…………(1)
…………（2)
（1)、(2)联立,可解得 和 。
至此,三个面的应力均为已知：X（ ，0），Y（ ，0）（ , 均为负值）;
( ）。由X，Y面的应力就可以作出应力圆。
[习题7-12]一焊接钢板梁的尺寸及受力情况如图所示,梁的自重略去不计。试示 上 三点处的主应力。
解:（1）求 点的主应力
解：坐标面应力：X（15,15）,Y(0，-15）
第一强度理论：
因为 ， ，即 ，
所以 符合第一强度理论的强度条件，构件不会破坏，即安全.
第二强度理论：
因为 ,
，即 ，
所以 符合第二强度理论的强度条件，构件不会破坏，即安全。
[习题7—25]一简支钢板梁承受荷载如图a所示，其截面尺寸见图b。已知钢材的许用应力为 , .试校核梁内的最大正应力和最大切应力。并按第四强度理论校核危险截面上的a点的强度。注:通常在计算a点处的应力时，近似地按 点的位置计算。

建筑力学,第七章应力和变形,武汉理工

建筑力学,第七章应力和变形,武汉理工

对于等截面直杆，最大正应力一定发生在轴力最大的截 面上。
max
FN max A
习惯上把杆件在荷载作用下产生的应力，称为工作应 力。 通常把产生最大工作应力的截面称为危险截面，产生 最大工作应力的点称为危险点。
对于产生轴向拉（压）变形的等直杆，轴力最大的截
面就是危险截面，该截面上任一点都是危险点。
T Ip
扭 转
横截面上距圆心为 处任一点切应力计算公式。
讨论：
T Ip
1）仅适用于各向同性、线弹性材料，在小变形时的等圆 截面直杆。
2）式中：T—横截面上的扭矩。
—该点到圆心的距离。
Ip—极惯性矩，纯几何量，无物理意义。
3）尽管由实心圆截面杆推出，但同样适用于空心圆截面 杆，只是Ip值不同。
υAC=υAB+υBC=（0.0319－ 0.0079）rad=0.024rad
弯曲应力
第五节 梁的正应力及正应力强度计算
a
A
FP
FP
横向线应变
FP
l l d d
a1
a
线应变--每单位长 度的变形，无量纲。
FP
l
l1
轴向拉伸和压缩
二、泊松比
从上述分析我们已经知道：杆件在轴向拉（压）变形
时，纵向线应变ε与横向线应变ε′总是正、负相反的。 通过实验表明：当轴向拉（压）杆的应力不超过材料 的比例极限时，横向线应变ε′与纵向线应变ε的比值的绝对 值为一常数，通常将这一常数称为泊松比或横向变形系数。 用μ表示。

FP FN
轴向拉伸和压缩
通过上述分析知：轴心拉杆横截面上只有一种应力——
正应力，并且正应力在横截面上是均匀分布的，所以拉杆横

材料力学第07章应力状态与应变状态分析

材料力学第07章应力状态与应变状态分析

以上由单元体公式
应力圆（原变换）
下面寻求： 由应力圆
单元体公式（逆变换）
只有这样，应力圆才能与公式等价
换句话，单元体与应力圆是否有一一对应关系？
为什么说有这种对应关系？
DE R sin[180o ( 2 20 )] R sin( 2 20 )
( R cos 20 ) sin 2 ( R cos 20 )cos 2
2
cos2
xy
sin 2
同理：
x
y
2
sin 2
xy
cos2
n
Ox
图2
二、极值应力
令:d
d
0
x
y
sin202 xycos200
由此得两个驻点：
01、（
01
2
）和两个极值：
tg20
2 xy x
y
y
mm
ax in
x
y ±（x
2
y
2
）2
2 xy
0 0极值正应力就是主应力 ！
y
O
x
七、主单元体、主平面、主应力：
y
y
主单元体(Principal bidy)：
x
各侧面上剪应力均为零的单元体。
z
z
2
3
主平面(Principal Plane)：
剪应力为零的截面。 x
主应力(Principal Stress ）：
主平面上的正应力。
1
主应力排列规定：按代数值大小，
1 2 3
三向应力状态（ Three—Dimensional State of Stress）： 三个主应力都不为零的应力状态。
A

材料力学 第七章 应力状态和强度理论

材料力学 第七章 应力状态和强度理论

y
2
2 xy
tan 2a0
2 xy x
y
max
1
2
3
主应力符号与规定： 1 2 3 （按代数值）
§7-3 空间应力状态
与任一截面相对应 的点，或位于应力 圆上，或位于由应 力圆所构成的阴影 区域内
max 1 min 3
max
1
3
2
最大切应力位于与 1 及 3 均成45的截面上
针转为正，顺时针转为负。
tg 2a 0
2 x x
y
在主值区间，2a0有两个解，与此对应的a0也有两个解，其中落
在剪应力箭头所指象限内的解为真解，另一解舍掉。
三、应力圆
由解析法知，任意斜截面的应力为
a
x y
2
a x
x
y
2
y cos2a
2
sin 2a x c
x s os2a
in
2a
广义胡克定律
1、基本变形时的胡克定律
1）轴向拉压胡克定律
x E x
横向变形
y
x
x
E
2）纯剪切胡克定律
G
y
x x
2、三向应力状态的广义胡克定律－叠加法
2
2
1
1
3
3
1
1
E
2
E
3
E
1
1 E
1
2
3
同理
2
1 E
2
3
1
广义胡克定律
3
1 E
3
1
2
7-5, 7-6
§7-4 材料的破坏形式
⒈ 上述公式中各项均为代数量，应用公式解题时，首先应写清已 知条件。

材料力学：第七章 应力、应变状态分析(下)

材料力学：第七章 应力、应变状态分析(下)
方法：根据测量所得的三个方向的线应变来 确定物体表面一点的主应变
❖ 解析法和几何法（图解法）
平面应变状态的应变分析
解析方法
实际测量时，采用由三个电阻 丝应变片组成的直角应变花，测量
三个方向的线应变e0、e45和e90。
由于ex=e0， ey=e90。
从而由
e90 e45 450
900
e0
e
ex
ey
可以证明：总存在一个特 殊的微元体，这个微元体 的每个侧面上只有正应力， 而没有切应力，此时的三 个正应力称为主应力。
y sy
tyx
tyz tzy
txy
sx
tzx txz x
sz
z
一. 三向应力圆
step1:求主应力
y sy
tyx
tyz tzy
txy
sx
tzx txz
x
sz
z
三向应力状态
s s s s x t xy t xz
任意方位的应变分析
yC
B
设有微元体，其边长为dx
和dy，棱边OA、OC的正应变
dy
e切直x，应 角e变y和AxO切y定C应的义变改为变x位y已量于知，原，并点这规O里的定
使直角增大为正。
o
y C
dx A x B
下面分析微元段OB的线应变 dy ——（ OB的伸长率） o dx A x
平面应变状态的应变分析
根据叠加原理，微元段OB的线 y
应变等于应变ex，ey和xy单独作用 C
时OB线应变的代数和，下面依次 dy
分析OB的线应变。
o
B
dx A x
1. 设微元体沿x方向的正应变
为 变e为x，则微元段OB的正应 y

材料力学课件第7章 应力状态分析

材料力学课件第7章 应力状态分析
α+
2
（2）主应力值计算 ） 方法一： 方法一： σ x +σ y σ x −σ y + cos 2α 0 − τ xy sin 2α 0 σ α =
2 2 0 σ x +σ y σ x −σ y π π σ = + cos 2 α 0 + − τ xy sin 2 α 0 + α0 + π 2 2 2 2 2
2τ xy
σ x −σ y
2τ xy 1 可取： 可取： α 0 = arctan − σ −σ 2 x y
1 2τ xy , arctan − σ −σ x y 2
π + 2来自3、主应力： 、主应力： （1）性质： ）性质： ①主应力为各截面上正应力的极值。 主应力为各截面上正应力的极值。
∗ FS Sz τ= bIz
五、主平面、主应力 主平面、 1、主平面 、 •τ= 0的截面 的截面; 的截面 •过一点有三个相 过一点有三个相 互垂直的主平面. 互垂直的主平面 2、主应力 、 •主平面上的正应力 主平面上的正应力; 主平面上的正应力 •表示符号 1 、σ2、σ3（ σ1 ≥σ2≥σ3 ） 。 表示符号σ 表示符号 应力状态分类： 六、应力状态分类： 1、单向应力状态： 只有一个主应力不为零。 、单向应力状态： 只有一个主应力不为零。 •可用平面图形表示应力状态。 可用平面图形表示应力状态。 可用平面图形表示应力状态 2、二向（平面）应力状态：两个主应力不为零。 、二向（平面）应力状态：两个主应力不为零。 •可用平面图形表示应力状态。 可用平面图形表示应力状态。 可用平面图形表示应力状态 3、三向应力状态 ：三个主应力都不为零。 三个主应力都不为零。 、 4、简单应力状态：单向应力状态。 、简单应力状态：单向应力状态。 5、复杂应力状态：二向和三向应力状态。 、复杂应力状态：二向和三向应力状态。

材料力学第17讲 Chapter7-1第七章 应力状态(解析法)

材料力学第17讲 Chapter7-1第七章 应力状态(解析法)

201 78.790， 01 39.3450 02 39.3450 - 900 -50.6550
12
41MPa -61MPa
39
Thank you for your attention!
作业： Page 250: 7-1(c,d);7-2 Page 251: 7-6
下次课讲应力圆
40
- xycsc20
02
01
2
将02也限制在[-900,900 ]，取 01 0 :02 01 900 01 0 :02 01 - 900
xy 0时：
大于零的那个角（第一象限角） 对应第一主应力
32
=0面上的切应力:
0
x
- y
2
sin 20
xy
x -y
2
cos 20
sin 2
x
dA
dA - x (dAcos)sin
xy
y
- xy (dAcos) cos xy (dAsin)sin
x ' y (dAsin)cos 0
x sin cos - y sin cos xy (cos2 - sin2 )
19
最后，得到以下两个方程：
x cos2 y sin2 - xy sin 2 x sin cos - y sin cos xy (cos2 - sin2 ) 引入 2 sincos sin2
27
主应力与主平面（二）
0
x
y
2
- xycsc20
1 0 y y
x
2 0 x
x
tg20
-
2 xy x -
y
(2) 若 xy 0, x y ;
tan 20 0, 0 0, csc20 0

材料力学 第07章 应力状态

材料力学 第07章 应力状态

C

D

平面应力状态通常用平面图形表示
A C


P
P




P
A B C D E
A
D
B
C
E
二. 应力分析的解析法
（1）斜截面应力
y
y
x
y
n

x
x
y
x x
y
x

x
y
y
n
Acos

A
Asin
σ：拉应力为正
τ：顺时针转动为正
α ：逆时针转动为正
2.斜面上的应力——微元体的平衡方程 平衡对象——用斜截 面截取的微元局部 参加平衡的量—— 应力乘以其作用的面积
A
A
B
B
B
C
C
主平面——切应力为零的平面 主应力——主平面上的正应力
可以证明： 受力构件的任一点可以找到三个相互垂直的主平面
即：受力构件的任一点有三个主应力
规定：按代数值大小排列成
1 2 3
主应力单元体——受主应力作用的单元体
A
A
四、应力状态的分类
单向应力状态 ——只有一个主应力不等于零的应力状态 二向应力状态 —— 有 二个主应力不等于零的应力状态 三向应力状态 —— 三个主应力都不为零的应力状态
4
解：
F 1 FSl 4 100kN 50kN 2 2 Fl 1 Ml 4 100kN 2m 25kN m 8 8
3
1 25 10 N m (- 600) 10 -3 m M 4 c y -1.04 106 Pa -1.04MPa 200 6003 Iz 10-12 m 4 12 Fs S 50 103 N 200 150 (150 75) 10 -9 m 3 c 0.469MPa 1 I zb 200 6003 10-12 m 4 200 10 -3 m 12

武汉理工大学材料力学(应力状态复习)资料重点

武汉理工大学材料力学(应力状态复习)资料重点

t
A
s
s1 81 MPa , s 2 0, s 3 31 MPa
或：
sr4
sr4 s 2 3t 2 100(MPa )
12（[ s1 s 2）2 （s 2 s 3）2 （s 3 s1）2 ]
12[s
2 1
s
2 3
(s
3
s
1
)2
]
12[812 312 (3181)2] 100(MPa )
十一、复杂应力状态下的强度条件
强度条件： s r ≤ [s ] 其中，sr—相当应力。
s1
相当
sr
sr
s2
s3
十二、相当应力
s r1 s1
s r2 s 1 s 2 s 3
sr3 s1 s 3
sr4
12[s1 s 2 2 s 2 s 3 2 s 3 s1 2]
十三、典型二向应力状态的相当应力
s3
一点的最大切应力为：
t
max
s
1
s
2
3
y s3 t
0 45
t
x
t s1 t
九、广义胡克定律
x
1 E
s
x
s
y
s
z
y
1 E
s
y
s z
s
x
z
1 E
sz
s
x
s
y
xy
t xy
G
yz
t yz
G
zx
t zx
G
1
1 E
s
1
s
2
s
3
2
1 E
s
2
s
3
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

s ydAsin2a t yxdAsina cosa 0
sa s x cos2a t xy cosa sina s y sin2a t yx sina cosa
由tyx=txy和三角变换，得：
sa

s
x
s
2
y

s
x
s
2
y
cos2a
t
xy
sin2a
sa

s
x
s
2
y

s
x
s
2
30
30° 30°
50
20
解： s x 50 , s y 30 ,
x
t xy 20 , a 30
s
30

s
x
s
2
y

s
x
s
2
y
cos2a
t
xy
sin2a
sa ta

50 2
30

50 2
30 cos
60

20sin60
12.7(MPa )
t
30

s
x
s
2
y
sin2a
tan 2a0
2t xy s x s y
2(30)
20
3
2a0 71.6
a0 35.8
F
A
Me
F Me
t
A
s
F
A
Me
s3
s1
F
Me
s1
a0 35.8
x
s3
§7–4 二向应力状态分析——图解法
txy
sa a
sx
ta
sy tyx
t
（1）应力圆（ Stress Circle）
一个主应力不为零的应力状态。
s1
s 1
2、二向应力状态（Plane State of Stress）：
二个主应力不为零的应力状态。
s1
s 2 s 1
3、三向应力状态（ Three—Dimensional State of Sstr2ess）：
三个主应力都不为零的应力状态。
s2 s3
s1
s1
s3
s2
§7–2 二向和三向应力状态的实例 [例1]画出图中的A点的应力单元体。
F
F
dx
dx
s
s
A
[例2] 画出图中A点的应力单元体。
A
Me
Me
t t
t
t
t
t
纯剪切应力状态
[例3] 画出图中各点的应力单元体。
F1
F2
q
1
2 3 4
5
M
FS
sM
FS
t
F1
F2
q
1
2 3 4
5
1
s
2
3
4
5
t
s
s
t max
1
s
s
1
F1
F2
q
1
2 3 4
5
1
s
1
s
2
3
4
5
t
t
s
s
t max
2
t
F1
s
60

s
x
s
2
y

s
x
s
2
y
cos2a
t
xy
sin2a

74 2

724 cos 120

(29)sin120
43.6(MPa )
t
60

s
x
s
2
y
sin2a
t
xy
cos2a
724sin120 (29)cos120
46.5(MPa )
s 60° t 60°
s 60° t 60°
44.7

54.7
34.7
∴ s1 54.7MPa
s2 0 s 3 34.7MPa
tan2a0


s
2t xy x s
y


220 50 30
tan 2a0 0.5
tan 2a0 0.5 2a0 26.56
a0 13.28
a0 76.72
A
二、最大正应力和最小正应力
s
a

s
x
s
2
y

s
x
s
2
y
cos2a
t
xy
s
in2a
sa
τxy
a
sx
ta
τyx
sy
sa 是a的周期函数，周期为
二、最大正应力和最小正应力
sa

s
x
s
2
y

s
x
s
2
y
cos2a
t
xy
sin2a
t xy
sx
令:
dsa da
0,
得：（s x s
y）sin2a 2t xy cos2a 0
b
15
z 270
15
sb
[例8 ] 求圆杆表面 A点的主应力及主平面。已知：F=6.28kN，
Me=47.1N·m，d=20mm。
F
A
F
s
t
t s
t
A
s
Me
Me
Me F
T FN
A
[例8 ] 求圆杆表面 A点的主应力及主平面。已知：F=6.28kN，
Me=47.1N·m，d=20mm。
t
s3
s1
F
122.5(MPa )
a
z 270
15
t
a

FS
S
* z
Izb

200103
[ 12015 (150 88106 9

7.5)
]
b
64.6(MPa )
ta
a
sa
s max s min


s
x
s
2
y

s
（
x
s
2
y
）2 t
2 xy

150MPa 27MPa
s1 150MPa , s 2 0, s 3 27MPa
（2）应力圆的画法 ①建立应力坐标系，如下图所示， （注意选好比例尺）
②在坐标系内画出点A(s x，txy) 和B(sy，tyx)
§7–3 二向应力状态分析——解析法
平面应力状态: 单元体有一对平面上的应力为零。
y
tyx
sx
sy
txy sx
txy
sx tyx
sy tyx
sx txy
z sy
x
sy
一、任意斜截面上的应力
二、最大正应力和最小正应力
三、主平面和主应力
四、应力圆（莫尔圆）
一、任意斜截面上的应力
已知：sx、 s y、txy 、a
sy
切应力为零的截面。
任意一点都可以找到三个相互垂直的主平面。
sx
（2）主应力(Principal Stress ）：
sz
主面上的正应力。
主应力排列规定：按代数值大小，
s1≥s2≥s3
s3
s1
s2
A
AA
五、应力状态分类
1、单向应力状态（Unidirectional State of Stress）：
A
F
s
Me
Me
解：s F 20(MPa )
A
Wt

d 3
16
t s
A
t a0
sx
t

s1
T
s3 30(MPa )
Wt
s s
max min


s
x
s
2
y

s
（
x
s
2
y
）2 t
2 xy

41.6MPa 21.6MPa
s1 41.6MPa , s 2 0, s 3 21.6MPa

s
x
s
2
y）2
t
2 a
（s
x
s
2
y）2
t
2 xy
（s a

s
x
s
2
y）2

t
2 a
（s
x
s
2
y）2
t
2 xy
与圆方程相比较： x a2 y2 R2
t
R
s
s x s y
2
R

s
（
x
s
2
y
）2 t
2 xy
此圆称为应力圆（或莫尔圆，由德国工程师：Otto Mohr引入）
sy tyz tyx
tzx
t tzy xy
sz txz
s x
sy
A
三、为什么要研究一点处的应力状态
A
A
F Me
l
A A
p
A
A
F F
s y云纹图
s x云纹图
t xy云纹图
F F
sy云纹图
s x云纹图
F
sy
sx
sx
txy
sy
F
四、主平面、主应力： （1）主平面(Principal Plane)：