元月调考压轴题

湖北省十堰市2024届高三元月调研考试理综高效提分物理试题（基础必刷）一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题一个物体做匀速圆周运动，会发生变化的物理量是（）A．角速度B．线速度C．周期D．转速第(2)题北京时间2023年11月1日6时50分，中国在太原卫星发射中心使用长征六号改运载火箭，成功发射天绘五号卫星。

已知该卫星进入预定轨道后围绕地球做匀速圆周运动，轨道离地高度为h（大约500km），地球的半径为R，地球表面附近重力加速度大小为g，忽略地球的自转，下列说法不正确的是（ ）A．天绘五号卫星在加速升空阶段处于超重状态，进入预定轨道后处于失重状态B．天绘五号卫星进入预定轨道后的运行速度大小为C．天绘五号卫星进入预定轨道后的向心加速度大小为D．天绘五号卫星进入预定轨道后的运行周期比同步卫星的运行周期小第(3)题如图甲所示，轻杆一端固定在O点，另一端固定一小球，现让小球在竖直平面内做半径为R的圆周运动。

小球运动到最高点时，受到的弹力为F，速度大小为v，其F—v2图像如图乙所示，则（ ）A．小球的质量为B．当地的重力加速度大小为C．v2=c时，小球对杆的弹力方向向下D．v2=2b时，小球受到的弹力与重力大小相等第(4)题如图，一辆汽车正在平直公路上以v0=72km/h的速度匀速行驶，突然在公路正前方52m处冲出三只小动物，司机立即刹车，设刹车过程是匀减速直线运动，加速度大小为4m/s2。

以下说法正确的是（ ）A．汽车在第4s末到第6s末的位移为2mB．汽车在第6s末的速度大小为4m/sC．做匀减速运动的汽车要撞上小动物D．汽车在第2s末的瞬时速度为10m/s第(5)题如图所示，竖直平面内有三根轻质细绳，绳1水平，绳2与水平方向成角，为结点，竖直绳3的下端栓接一质量为、长度为的垂直于纸面放置的金属棒。

金属棒所在空间存在竖直向上，磁感应强度大小为B的匀强磁场，整个装置处于平衡状态。

山西省太原市高三元月调考数学试卷（理科）姓名:________ 班级:________ 成绩:________一、选择题： (共12题；共24分)1. （2分）有如下结论：①m∈（P∪Q）⇒m∈P；②m∈（P∩Q）⇒m∈（P∪Q）；③P⊆Q⇒P∪Q＝Q；④P∪Q ＝P⇒P∩Q＝Q．其中正确的个数是（）A . 1个B . 2个C . 3个D . 4个2. （2分）复数z1=3+i,z2=1－i，则z=z1·z2在复平面内的对应点位于（）A . 第一象限B . 第二象限C . 第三象限D . 第四象限3. （2分） (2017高一下·南昌期末) 某程序框如图所示，若输出的S=57，则判断框内应为（）A . k＞6？B . k＞5？C . k＞4？D . k＞3？4. （2分） (2017高一上·西城期中) 函数与的图象交点为，则所在区间是（）．A .B .C .D .5. （2分） (2018高二下·枣庄期末) 甲乙二人争夺一场围棋比赛的冠军，若比赛为“三局两胜”制，甲在每局比赛中获胜的概率均为，各局比赛结果相互独立且没有平局，则在甲获得冠军的情况下，比赛进行了三局的概率为（）A .B .C .D .6. （2分）(2017·东城模拟) 某三棱锥的三视图如图所示，则该三棱锥的体积为（）A .B .C . 1D .7. （2分）(2017·荆州模拟) a= （﹣cosx）dx，则（ax+ ）9展开式中，x3项的系数为（）A . ﹣B . ﹣C .D .8. （2分）将所有的自然数按以下规律排列：0123456789101112…那么从2012到2014的顺序为（）A . →↑B . ↑→C . ↓→D . →↓9. （2分）函数f（x）=的大致图象是（）A .B .C .D .10. （2分） (2016高二上·潮阳期中) 若log4（3a+4b）=log2 ，则a+b的最小值是（）A . 6+2B . 7+2C . 6+4D . 7+411. （2分）(2017·成都模拟) 设双曲线C：（a＞0，b＞0）的左右焦点分别为F1 ， F2 ，以F1F2为直径的圆与双曲线左支的一个交点为P，若以OF1（O为坐标原点）为直径的圆与PF2相切，则双曲线C的离心率为（）A .B .C .D .12. （2分）已知tanα=2，tanβ=3，且α、β都是锐角，则α+β=（）A .B .C . 或D . 或二、填空题： (共4题；共4分)13. （1分） (2017高三下·成都期中) 斜率为k（k＞0）的直线l经过点F（1，0）交抛物线y2=4x于A，B 两点，若△AOF的面积是△BOF面积的2倍，则k=________．14. （1分）函数f（x）= 的最大值是________．15. （1分）已知=（1，0），=（2，3），则（2﹣）•（+）=________16. （1分）(2018·梅河口模拟) 在四面体中，平面，，，点为的重心，若四面体的外接球的表面积为，则 ________.三、解答题： (共7题；共65分)17. （10分） (2016高一下·辽源期中) 在等比数列{an}中，a1=2，a4=16（1）求数列{an}的通项公式；（2）令，n∈N*，求数列{bn}的前n项和Sn．18. （10分）如图，在三棱锥P﹣ABC中，PA⊥PC，PB=AB=BC=2，∠ABC=120°，，D为AC上一点，且AD=3DC．（1）求证：PD⊥平面ABC；（2）若E为PA中点，求直线CE与平面PAB所成角的正弦值．19. （15分）(2018·丰台模拟) 某地区工会利用“健步行”开展健步走积分奖励活动．会员每天走5千步可获积分30分(不足5千步不积分)，每多走2千步再积20分（不足2千步不积分）．记年龄不超过40岁的会员为类会员，年龄大于40岁的会员为类会员．为了解会员的健步走情况，工会从两类会员中各随机抽取名会员，统计了某天他们健步走的步数，并将样本数据分为，，，，，，，，九组，将抽取的类会员的样本数据绘制成频率分布直方图，类会员的样本数据绘制成频率分布表（图、表如下所示）．（1）求和的值；（2）从该地区类会员中随机抽取名，设这名会员中健步走的步数在千步以上（含千步）的人数为，求的分布列和数学期望；（3）设该地区类会员和类会员的平均积分分别为和，试比较和的大小（只需写出结论）．20. （5分） (2017高二上·牡丹江月考) 已知抛物线的焦点，为坐标原点，是抛物线上异于的两点，若直线的斜率之积为，求证：直线过轴上一定点。

湖北省十堰市2024届高三元月调研考试理综高效提分物理试题一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题下图是家庭里常见的厨房水槽，A、B分别是水槽出口上的两点，当出水口绕转轴O转动，如下图，v代表线速度，代表角速度，a代表向心加速度，T代表周期，则下列说法正确的是（）A．，B．，C．，D．，第(2)题利用霍尔效应可将直流电转化为交流电，如图所示，宽度为h、厚度为d的霍尔元件放在与它垂直的磁感应强度大小为的磁场中（竖直向下为磁场正方向），当恒定电流I向右通过霍尔元件时，在它的两个表面之间会产生霍尔电压，已知该霍尔元件中的载流子为电子，电荷量大小为e，每单位体积内有n个电子，下列说法正确的是（ ）A ．时，霍尔元件上表面的电势高于下表面B ．时，霍尔元件前侧面的电势低于后侧面C．输出霍尔电压的表达式为D．输出霍尔电压的有效值为第(3)题如图所示，在正方形ABCD的四个顶点上分别固定一个点电荷，四个点电荷的电荷量相等，正方形中心O点的电势为正，电场强度不为零，分别为的中点，P点场强比Q点场强大，取无穷远处为零电势点，则正方形四个顶点的点电荷中（ ）A．有两个带负电B．有三个带负电C．两点的点电荷带同种电荷D．两点的点电荷带同种电荷第(4)题如图所示，电子在电场中从a点运动到b点，实线为电场线，虚线为电子的运动轨迹，请判断下列说法正确的是（ ）A．a点的电势低于b点的电势B．电子在a点的加速度大于在b点的加速度C．电子在a点的速度大于在b点的速度D．电子在a点的电势能大于在b点的电势能第(5)题如图所示，小物块a、b和c静置于光滑水平地面上。

现让a以速度v向右运动，与b发生正碰，然后b与c也发生正碰。

若a、b、c的质量可任意选择，碰撞可以是弹性也可以是非弹性的，各种可能的碰撞后，c的最大速度为（）A．4v B．6v C．9v D．12v第(6)题以下物理量为标量，且单位是国际单位制导出单位的是（ ）A．电流、A B．力、N C．功、J D．电场强度、N/C第(7)题汤姆孙利用电子束穿过铝箔，得到如图所示的衍射图样。

2021届高三数学元月调研考试试题 文〔含解析〕本卷贰O 贰贰年贰月捌日编写； 出题人：令狐学复；欧阳化语；令狐理总。

一、选择题：此题一共12小题，每一小题5分，一共60分．在每一小题给出的四个选项里面，只有一项是哪一项符合题目要求的．{}1,2,3,4,5A =，{}|3B x x =-<-，那么A B =〔 〕A. {}5B. {}1,2C. {}3,4,5D. {}4,5【答案】D 【解析】 【分析】首先求出集合B ，再根据交集的定义，即可得解. 【详解】解：因为{}|3B x x =-<-{}|3B x x ∴=>，{}1,2,3,4,5A ={}4,5A B ∴=.应选：D【点睛】此题考察交集的运算，属于根底题.5iz i=+上的虚部为〔 〕 A. 526 B.526i C. 526-D. 526i -【答案】A 【解析】 【分析】 化简得到152626z i =+计算虚部得到答案. 【详解】()515262626i i z i-==+，所以5i z i =+的虚部为526. 应选：A【点睛】此题考察了复数虚部的计算，属于简单题.3.,αβ是两个不同的平面，,m l 是两条不同的直线，且,,m l αβααβ⊥⊂⋂=，那么“m l ⊥〞是“m β⊥〞的〔 〕条件 A. 充分不必要 B. 必要不充分C. 充要D. 既不充分也不必要【答案】C 【解析】 【分析】由面面垂直的性质定理、线面垂直的概念，结合充分、必要条件，判断出正确选项.【详解】假设m l ⊥，根据面面垂直的性质定理可知m β⊥；假设m β⊥，那么由l β⊂可得m l ⊥.所以“m l ⊥〞是“m β⊥〞的充要条件 应选：C.【点睛】本小题主要考察面面垂直的性质定理，考察充分、必要条件的判断，属于根底题.4.某地有两个国家AAAA 级旅游景区——甲景区和乙景区.相关部门统计了这两个景区2021年1月至6月的月客流量〔单位：百人〕，得到如下图的茎叶图.关于2021年1月至6月这两个景区的月客流量，以下结论错误的选项是．．．．．．〔 〕A. 甲景区月客流量的中位数为12950人B. 乙景区月客流量的中位数为12450人C. 甲景区月客流量的极差为3200人D. 乙景区月客流量的极差为3100人 【答案】D【解析】 【分析】分别计算甲乙景区流量的中位数和极差得到答案. 【详解】根据茎叶图的数据：甲景区月客流量的中位数为12950人，乙景区月客流量的中位数为12450人. 甲景区月客流量的极差为3200人，乙景区月客流量的极差为3000人. 应选：D【点睛】此题考察了茎叶图中位数和极差的计算，意在考察学生的应用才能. 5.执行下边的程序框图，假设输入的x 的值是5，那么输出的n 的值是〔 〕A. 2B. 3C. 4D. 5【答案】C 【解析】 【分析】根据程序框图依次计算得到答案.【详解】执行程序框图：(),x n 依次为()5,0，()7,1，()9,2，()11,3，()13,4∵21313132+> ∴输出的n 的值是4. 应选：C【点睛】此题考察了程序框图的计算，意在考察学生对于程序框图的理解才能.ln(),0()()1,0x x f x g x x -<⎧=⎨+>⎩假设()f x 是奇函数，那么()2g e =( )A. -3B. -9C. -1D. 1【答案】A 【解析】 【分析】首先根据函数()f x 是奇函数可得()()222f ef e =--=-，又()()221g e f e =-，据此即可求出结果.【详解】因为函数()f x 是奇函数，所以()()222ln 2f e f e e=--=-=-，又()()221g ef e =-，所以()23g e =-.应选：A.【点睛】此题主要考察了函数的奇偶性，以及利用分段函数求函数值，属于根底题.{}n a 的前n 项和为n S ，且54S =，1010S =，那么15S =〔 〕A. 16B. 19C. 20D. 25【答案】B 【解析】 【分析】利用5S ，105S S -，1510S S -成等比数列求解【详解】因为等比数列{}n a 的前n 项和为n S ，所以5S ，105S S -，1510S S -成等比数列，因为54S =，1010S =，所以1056S S -=，15109S S -=，故1510919S =+=.应选：B【点睛】此题考察等比数列前n 项性质，熟记性质是关键，是根底题sin 2y x =向左平移()0ϕϕ>个单位长度，得到曲线5cos 26y x π⎛⎫=+⎪⎝⎭，那么tan ϕ=〔 〕B.D. 【答案】B 【解析】 【分析】变换得到sin 2cos 22x x π⎛⎫=-⎪⎝⎭，根据平移得到()23k k πϕπ=+∈N ，计算得到答案. 【详解】sin 2cos 22x x π⎛⎫=- ⎪⎝⎭，所以52cos 2cos 2632x x πππ⎡⎤⎛⎫⎛⎫+=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，所以()23k k πϕπ=+∈N ，那么tan ϕ=应选：B【点睛】此题考察了三角函数的平移，变换sin 2cos 22x x π⎛⎫=- ⎪⎝⎭是解题的关键.24y x =的焦点为F ，M ，N 是该抛物线上的两点，且12MF NF +=，那么线段MN 的中点到x 轴的间隔 是〔 〕 A.14B.18C.316D.516【答案】C 【解析】 【分析】先判断线段MN 的中点到其准线的间隔 是14，再计算到x 轴的间隔 . 【详解】12MF NF +=，所以线段MN 的中点到其准线的间隔 是14由题意可知18p =，那么线段MN 的中点到x 轴的间隔 是134216p -=.应选：C【点睛】此题考察了抛物线上的点到准线的间隔 问题，意在考察学生的转化才能和计算才能.()1cos 2cos x f x x+=+，()()20g x ax a =->.假设1x R ∀∈，[]21,2x ∃∈，()()12f x g x =，那么a 的取值范围是〔 〕 A. 21,3⎡⎤⎢⎥⎣⎦B. 2,23⎡⎤⎢⎥⎣⎦C. 4,23⎡⎤⎢⎥⎣⎦D. 4,3⎡⎫+∞⎪⎢⎣⎭【答案】C 【解析】 【分析】根据条件求出()f x 的值域，与()g x 的值域，由1x R ∀∈，[]21,2x ∃∈，()()12f x g x =，可得两值域的包含关系，即可求得参数a 的取值范围. 【详解】解：因为()2cos 1112cos 2cos x f x x x +-==-++，12cos 3x +，所以()f x 的值域为20,3⎡⎤⎢⎥⎣⎦.因为0a >，所以()g x 在[]1,2上的值域为[]2,22a a --，依题意得[]20,2,223a a ⎡⎤⊆--⎢⎥⎣⎦，那么20,222,3a a -⎧⎪⎨-⎪⎩解得423a . 应选：C【点睛】此题考察函数方程思想的综合应用，属于中档题.1所示，它的盛酒局部可以近似地看作是半球与圆柱的组合体〔如图2)．当这种酒杯内壁外表积〔假设内壁外表光滑，外表积为S 平方厘米，半球的半径为R 厘米〕固定时，假设要使得酒杯的容积不大于半球体积的2倍，那么R 的取值范围为( )A. ⎛ ⎝B. ⎫+∞⎪⎪⎭C. D. 【答案】D 【解析】 【分析】根据题意，酒杯内壁外表积为圆柱与半球的外表积，列出S 的表达式，再求出体积V ，解不等式即可． 【详解】解：设圆柱的高度与半球的半径分别为h ，R ，那么222S R Rh ππ=+，那么22SRh R ππ=-， 所以酒杯的容积323233224()332323S S V R R h R R R R R R ππππππ=+=+-=-+，又0h >，所以202SR π->， 所以22523S R R ππ<2S R ππ<， 应选：D ．【点睛】考察了组合体的体积和外表积计算，属于中档题．()222210,0x y a b a b-=>>的左、右焦点分别为1F ，2F ，渐近线分别为1l ，2l ，过点1F 且与1l 垂直的直线l 交1l 于点P ，交2l 于点Q ，假设12PQ F P =，那么双曲线的离心率为〔 〕A .C. 2D. 3【答案】B 【解析】 【分析】设1l ：b y x a =-，2l ：by x a =，联立方程得到2,a ab P c c ⎛⎫-⎪⎝⎭，再计算2PQ b =，OQ =利用余弦定理得到4224430c a c a -+=，计算得到答案. 【详解】记O ()1,0F c -，不妨设1l ：b y x a =-，2l ：by x a=那么直线l ：()a y x c b =+.联立()a y x c b b y x a ⎧=+⎪⎪⎨⎪=-⎪⎩，解得2a x cab y c ⎧=-⎪⎪⎨⎪=⎪⎩那么2,a ab P c c ⎛⎫-⎪⎝⎭故1PF b =，OP a =.因为12PQ F P =，所以12PQ PF = 所以2PQ b =，OQ =22221cos QOF ∠=.因为2tan b QOF a ∠=，所以2cos a QOF c∠=，22220ac=，整理得4224430c a c a -+=，那么42430e e -+=解得e =应选：B【点睛】此题考察了双曲线的离心率问题，综合性强，计算量大，意在考察学生的综合应用才能和计算才能.二、填空题：本大题一一共4小题，每一小题5分，一共20分．()e x f x mx =-在[2,0]-上为减函数，那么m 的取值范围为___________.【答案】[)1,+∞ 【解析】 【分析】将问题转化为导函数在[]2,0-上恒小于零，从而根据恒成立思想求解出m 的取值范围. 【详解】由题意可知()e 0xf x m '=-≤，即x m e ≥对[2,0]x ∈-恒成立， 所以()maxxm e≥，所以0e 1m ≥=即[)1,m ∈+∞. 故答案为：[)1,+∞.【点睛】此题考察根据函数的单调性求解参数范围，难度一般.函数()f x 为指定区间的单调增(或者减)函数，那么()()()00f x f x ''≥≤在指定区间上恒成立.14.第28届金鸡百花电影节将在举办，近日首批影展片单揭晓，?南方车站的聚会??春江水暖??第一次的离别??春潮??抵达之谜?五部优秀作品将在电影节进展展映．假设从这五部作品中随机选择两部放在展映的前两位，那么?春潮?与?抵达之谜?至少有一部被选中的概率为 _____． 【答案】710. 【解析】 【分析】首先根据题意，列举出从这五部作品中随机选择两部放在展映的前两位的所有情况，一共10种情况，其中?春潮?与?抵达之谜?至少有一部被选中的有7种，根据古典概型概率计算公式即可求结果. 【详解】从这五部作品中随机选择两部放在展映的前两位的所有情况为〔?南方车站的聚会?，?春江水暖?〕，〔?南方车站的聚会?，?第一次的离别?〕，〔?南方车站的聚会?，?春潮?〕，〔?南方车站的聚会?，?抵达之谜?〕，〔?春江水暖?，?第一次的离别?〕，〔?春江水暖?，?春潮?〕，〔?春江水暖?，?抵达之谜?〕，〔?第一次的离别?，?春潮?〕，〔?第一次的离别?，?抵达之谜?〕，〔?春潮?，?抵达之谜?〕，一共10种情况，其中?春潮?与?抵达之谜?至少有一部被选中的有7种，故所求概率为710. 故答案为：710. 【点睛】此题主要考察了古典概型概率的计算，属于根底题.ABC ∆满足“勾3股4弦5〞，其中“股〞4AB =，D 为“弦〞BC 上一点〔不含端点〕，且ABD ∆满足勾股定理，那么()CB CA AD -⋅=______. 【答案】14425【解析】 【分析】先由等面积法求得AD ，利用向量几何意义求解即可.【详解】由等面积法可得341255AD ⨯==，依题意可得，AD BC ⊥， 所以()214425CB CA AD AB AD AD -⋅=⋅==.故答案为：14425【点睛】此题考察向量的数量积，重点考察向量数量积的几何意义，属于根底题.{}n a 中，13a =，且()()12(1)22n n n a n a n +-=++-〔1〕{}n a 的通项公式为________； 〔2〕在1a ，2a ，3a ，，2019a 这2021项中，被10除余2的项数为________.【答案】 (1). 222n a n n =-+ (2). 403【解析】 【分析】〔1〕等式两边同除()1n n +构造数列为等差数列即可求出通项公式； 〔2〕利用通项公式及被10除余2 的数的特点即可求解 【详解】〔1〕因为()()12(1)22n n n a n a n +-=++-，所以122221n n n a a n a n n n+-+--==+2+，即12221n n a a n n +---=+，那么2n a n -⎧⎫⎨⎬⎩⎭为等差数列且首项为1，差为2，所以212(1)n a n n -=+- 21n =-，故222n a n n =-+〔2〕因为(21)2n n n a =-+，所以当n 能被10整除或者n 为偶数且21n -能被5整除时，n a 被10除余2，所以8,10,18,20,,2010,2018n =，故被10除余2的项数为201014035+=. 故答案为：222n a n n =-+；403【点睛】此题考察数列的通项，考察构造法，注意解题方法的积累，属于中档题．三、解答题：一共70分．解容许写出文字说明、证明过程或者演算步骤，第17～21题为必考题，每道试题考生都必须答题．第22、23题为选考题，考生根据要求答题． 〔一〕必考题：一共60分．17.某土特产超为预估2021年元旦期间游客购置土特产的情况，对2021年元旦期间的90位游客购置情况进展统计，得到如下人数分布表.〔1〕求购置金额不少于45元的频率；〔2〕根据以上数据完成22⨯列联表，并判断是否有95%的把握认为购置金额是否少于60元与性别有关.附：参考公式和数据：()()()()()22n ad bcKa b c d a c b d-=++++，n a b c d=+++.附表：)2k【答案】〔1〕12〔或者0.5〕；〔2〕列联表见解析，有95%的把握认为购置金额是否少于60元与性别有关.【解析】【分析】〔1〕根据统计表及古典概型的概率计算公式即可计算出不少于45元的频率；〔2〕完善列联表，计算出2K 跟参考数据比拟得出结论. 【详解】解：〔1〕购置金额不少于45元的频率为1520101902++=.〔2〕22⨯列联表如下：()22901220401814405 3.84130605238247K ⨯⨯-⨯==>>⨯⨯⨯，因此有95%的把握认为购置金额是否少于60元与性别有关.【点睛】此题考察HY 性检验，以及古典概型的概率计算问题，属于根底题.23()cos sin 2f x x x x =+-，a ，b ，c 分别为ABC ∆内角A ，B ，C 的对边.()0f A =，2b =.〔1〕假设a =B ；〔2〕假设2a c =，求ABC ∆的面积.【答案】(1) 6B π=. (2)6【解析】 【分析】〔1〕运用二倍角正余弦公式和辅助角公式，化简f 〔x 〕，并求得3A π=，再利用正弦定理求得1sin 2B =，可得结论；〔2〕由三角形的余弦定理得13c -+=结合面积公式，求得b ，c 的关系，即可得到所求三角形的周长．【详解】〔1〕31cos23()sin 2sin 212226x f x x x π-⎛⎫=+-=-- ⎪⎝⎭， 因为()0f A =，所以262A ππ-=，即3A π=.因为sin sin a b A B=，所以sin 1sin 2b A B a ==， 因为(0,)B π∈，所以6B π=或者56π， 又b a <，所以6B π=.〔2〕由余弦定理，可得222(2)222cos3c c c π=+-⨯⨯，即23240c c +-=，解得1133c -+=〔负根舍去〕， 故ABC ∆的面积为11113393sin 2sin 22336bc A π-+-=⨯⨯⨯=【点睛】此题考察三角函数的恒等变换，正弦函数的图形和性质，考察解三角形的余弦定理和面积公式，考察化简整理的运算才能，属于中档题．19.如图，在正方体1111ABCD A B C D -中，F ，G 分别是棱1CC ，1AA 的中点，E ，M 分别为棱AB ，11A B 上一点，113B M MA =，且GM 平面1B EF .〔1〕证明：E 为AB 的中点. 〔2〕假设四棱锥1F B MGE -的体积为32，求正方体1111ABCD A B C D -的外表积. 【答案】〔1〕见解析；〔2〕24 【解析】【分析】〔1〕取11A B 的中点N ，连接AN ，可证GM AN ，再由线面平行得到1ANB E ，又1B NAE ，所以四边形1AEB N 为平行四边形，即可得证.〔2〕设棱长为a ，易知F 到平面11ABB A 的间隔 为a ，由1113F B MGE B MGE V h S -=⋅⋅求出a 的值，即可求出外表积.【详解】解：〔1〕证明：取11A B 的中点N ，连接AN因为113B M MA =，所以M 为1A N 的中点，又G 为1AA 的中点，所以GM AN .因为GM 平面1B EF ，GM ⊂平面11ABB A ，平面11ABB A 平面11B EF B E =.所以1GM B E ，即1AN B E .又1B NAE ，所以四边形1AEB N 为平行四边形，那么1AE B N =，所以E 为AB 的中点.〔2〕设AB a ，那么1A MG ∆，AGE ∆，1BEB ∆的面积分别为2a 16，28a ，24a ，易知F 到平面11ABB A 的间隔 为a ，所以11222321133331684162F B MGEB MGE a a a a V h S a a -⎛⎫==⋅⋅⨯---⨯== ⎪⎝⎭， 解得2a =，故所求正方体的外表积为2624a =.【点睛】此题考察锥体的体积计算以及线面平行的性质，属于根底题.()2222:10x y a b a bΩ+=>>的焦距为2622〔1〕求Ω的方程；〔2〕假设直线2y x =+与Ω相交于A 、B 两点，求以线段AB 为直径的圆的HY 方程.【答案】〔1〕22182x y +=；〔2〕2282485525x y ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭. 【解析】 【分析】〔1〕根据题意求出a 和b 的值，即可求出椭圆Ω的方程；〔2〕设点()11,A x y 、()22,B x y ，将直线AB 的方程与椭圆Ω的方程联立，列出韦达定理，求出线段AB 的中点和AB ，即可得出所求圆的HY 方程.【详解】〔1〕设椭圆Ω的焦距为()20c c >，那么2c =，2b =所以c =b =2228a b c =+=，所以Ω的方程为22182x y +=；〔2〕设点()11,A x y 、()22,B x y ，联立222182y x x y =+⎧⎪⎨+=⎪⎩，消去y ，得251680x x ++=.由韦达定理得12165x x +=-，1285x x =， 所以12825x x +=-，线段AB 的中点坐标为82,55⎛⎫- ⎪⎝⎭.12AB x x =-===， 所以，所求圆的HY 方程为2282485525x y ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭.【点睛】此题考察椭圆方程的求解，同时也考察了直线截圆所得弦长的计算以及圆的HY 方程的求解，一般将直线方程与椭圆方程联立，利用韦达定理设而不求法来计算，考察运算求解才能，属于中等题.()()33114ln 10f f x ax x x '=--的图象在点()()1,1f 处的切线方程为100++=x y b .〔1〕求a ，b 的值； 〔2〕假设()13f x m >对()0,x ∈+∞恒成立，求m 的取值范围.【答案】〔1〕13a =,403=-b〔2〕2642ln 2<-m 【解析】 【分析】〔1〕求导可得()()23114310f f x ax x''=--,由题,切线方程斜率为()1f k '=,解得13a =,代回函数求得()1013f =,即10103b =--,可求得403=-b ； 〔2〕假如求()13f x m >对0x ∈+∞（，）恒成立,即求()min 13f x m >,利用导数判断单调性求得最小值即可求解不等式【详解】解：〔1〕()()23114310f f x ax x''=--, 因为()f x 在()()1,1f 处的切线方程为100++=x y b ,即10y x b =--,此时切线斜率10k =-,那么()3(1)13141010f f a k ''=--==-,解得13a =,所以()()333101114ln 314ln 3103f x x x x x x x ⨯-=--=+-, 所以()31110113114ln13333f =⨯+⨯-=+=,那么10103b =--,解得403=-b〔2〕由〔1〕知()31314ln 3f x x x x =+-,()32143143x x f x x x x+-'=+-=, 设函数()()33140g x x x x =+->,那么()2330g x x '=+>,所以()g x 在()0,∞+为增函数,因为()20g =,令()0g x <,得02x <<；令()0g x >,得2x >, 所以当02x <<时,()0f x '<；当2x >时,()0f x '>, 所以()()3min 126223214ln 214ln 233f x f ==⨯+⨯-=-,从而12614ln 233<-m ,即2642ln 2<-m 【点睛】此题考察利用导数的几何意义求值,考察利用导数研究不等式恒成立问题,考察转化思想,考察运算才能〔二〕选考题：一共10分，请考生在第22、23题中任选一题答题，假如多做，那么按所做的第一题计分．xOy 中，直线l的参数方程为212x t y ⎧=-⎪⎪⎨⎪=+⎪⎩〔t 为参数〕，曲线C 的参数方程为cos sin x m y a n αα=⎧⎨=+⎩〔0m >，0n >，α为参数〕，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，且曲线C 的极坐标方程为8sin ρθ=.〔1〕求a ，m ，n 的值；〔2〕点P 的直角坐标为()0,1，l 与曲线C 交于A ，B 两点，求PA PB +. 【答案】〔1〕4a m n ===；〔2. 【解析】 【分析】〔1〕根据极坐标方程得到()22416x y +-=，根据参数方程得到答案.〔2〕将参数方程代入圆方程得到270t --=，根据韦达定理得到120t t +=>，1270t t =-<，计算12PA PB t t +=-得到答案.【详解】〔1〕由8sin ρθ=，得28sin ρρθ=，那么228x y y +=，即()22416x y +-=.因为0m >，0n >，所以4a m n ===.〔2〕将21x t y ⎧=-⎪⎪⎨⎪=⎪⎩代入()22416x y +-=，得270t --=.设A ，B 两点对应的参数分别为1t ，2t ，那么120t t +=>，1270t t =-<.所以12t t P PB A =-==+.【点睛】此题考察了极坐标方程和参数方程，利用直线的参数方程可以简化计算，是解题的关键.()3124f x x x =+--.〔1〕求不等式()3f x >的解集；〔2〕假设对任意x ∈R ，不等式()228f x x t t --≤-恒成立，求t 的取值范围，【答案】〔1〕4(,10),5⎛⎫-∞-+∞ ⎪⎝⎭；〔2〕(][),19,-∞-+∞.【解析】 【分析】〔1〕利用分段讨论法去掉绝对值，求出不等式()3f x >的解集；〔2〕利用绝对值三角不等式求出()2f x x --的最大值，得出关于t 的不等式，求出解集即可． 【详解】〔1〕当1x <-时，()3(1)(24)3f x x x =-++->，解得10x <-； 当12x -≤≤时，()3(1)(24)3f x x x =++->，解得45x >，那么425x <≤；当2x >时，()3(1)(24)3f x x x =+-->，解得4x >-，那么2x >. 综上，不等式()3f x >的解集为4(,10),5⎛⎫-∞-+∞ ⎪⎝⎭； 〔2〕()|2|3|1||24||2|f x x x x x --=+----3|1|3|2|x x =+--|33||36|x x =+--|33(36)|9x x ≤+--=，假设对任意x ∈R ，不等式2()|2|8f x x t t --≤-恒成立， 那么289t t -≥，解得1t ≤-或者9t ≥. 因此，实数t 的取值范围是(][),19,-∞-+∞.【点睛】此题考察了含有绝对值的不等式解法与应用，同时考察了不等式恒成立问题，属于中档题．本卷贰O贰贰年贰月捌日编写；出题人：令狐学复；欧阳化语；令狐理总。

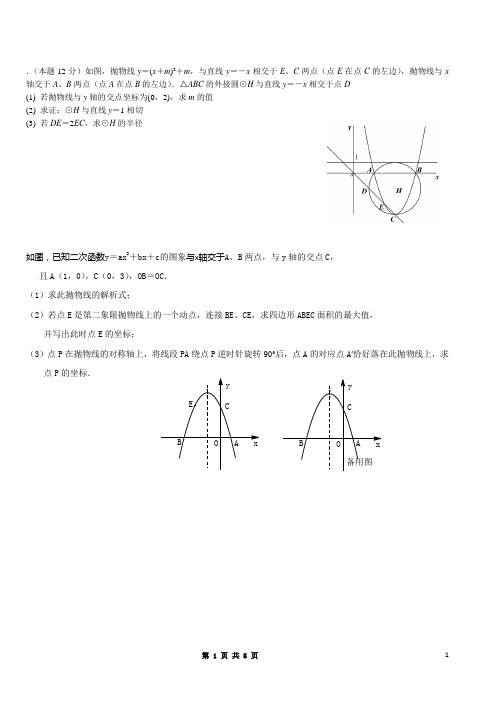
A BCOxy 备用图yx O ECBA ．（本题12分）如图，抛物线y ＝(x ＋m )2＋m ，与直线y ＝－x 相交于E 、C 两点（点E 在点C 的左边），抛物线与x 轴交于A 、B 两点（点A 在点B 的左边）．△ABC 的外接圆⊙H 与直线y ＝－x 相交于点D (1) 若抛物线与y 轴的交点坐标为(0，2)，求m 的值 (2) 求证：⊙H 与直线y ＝1相切 (3) 若DE ＝2EC ，求⊙H 的半径如图，已知二次函数y ＝ax 2＋bx ＋c 的图象与x 轴交于A 、B 两点，与y 轴的交点C ， 且A （1，0），C （0，3），OB ＝OC ． （1）求此抛物线的解析式；（2）若点E 是第二象限抛物线上的一个动点，连接BE 、CE ，求四边形ABEC 面积的最大值，并写出此时点E 的坐标；（3）点P 在抛物线的对称轴上，将线段PA 绕点P 逆时针旋转90°后，点A 的对应点A ′恰好落在此抛物线上，求点P 的坐标．在直线321+=x y 上取点A (2，4)、B ，使∠AOB ＝90°，求点B 的坐标 小明同学是这样思考的，请你和他一起完成如下解答：将线段OA 绕点O 逆时针旋转90°得到OC ，则点C 的坐标为：___________ 所以，直线OC 的解析式为：____________________点B 为直线AB 与直线OC 的交点，所以，点B 的坐标为：___________ 问题应用：已知抛物线353191929122++-+-=m m mx x y 的顶点P 在一条定直线l 上运动(1) 求直线l 的解析式(2) 抛物线与直线l 的另一个交点为Q ，当∠POQ ＝90°时，求m 的值已知抛物线m mx x y 223212--=交x 轴于A (x 1，0)、B (x 2，0)，交y 轴于C 点，且x ＜0＜x 2，(AO ＋OB )2＝12CO ＋1 (1) 求抛物线的解析式 (2) 求△ABC 内切圆半径(3) 请分别求出：在x 轴的下方且在抛物线上的点P ，使∠APB 为锐角，∠APB 为钝角时，P 点的横坐标的取值范围本题12分）已知抛物线y ＝ax 2＋bx ＋c 与y 轴交于A (0，－4)，与x 轴交于B 、C 两点，且B (－2，0)、C (4，0)(1) 求抛物线的解析式(2) 如图1，若点M 在y 轴上，且∠BMO ＋∠OAB ＝∠ACB ，求点M 的坐标(3) 如图2，将抛物线y ＝ax 2＋bx ＋c 向右平移n （n ＞0）个单位得到的新抛物与x 轴交于M 、N （M 在N 左侧），P 为x 轴下方的新抛物线上任意一点，连PM 、PN ，过P 作PQ ⊥MN 于Q ，NQPQMQ PQ是否为定值?请说明理由如图,等腰直角△ABC 内接于⊙O,D 为⊙O 上一点,连接AD 、BD 、CD (1)如图(1),点D 在半圆BC 上时,求证:BD+CD=22AD;(2)如图(2),点D 在劣弧AB 上时,直接写出BD 、CD 、AD 间的数量关系:CD-BD=2AD; (3)在(2)的条件下,如图(3),CD 与AB 交于点E,连接AO 交CD 于F,若AE=3BE,AF=2,求⊙O 的直径.19.如图,△ABC 中,AB ＝AC ,以AB 为直径的⊙O 分别与边BC 和AC 相交于点E 和F ,过E 作⊙O 的切线交边AC 于H .(1)求证:CH ＝FH ;(2)如图2,连接OH ,若OH ＝7,HC ＝1,求⊙O 的半径.图1C FHEOBA ABOEHFC图220.如图,在Rt △ABC 中,∠C ＝90°,∠A ＝30°,BC ＝3.P 为AC 边上一动点,PC ＝t ,以点P 为中心,将△ABC 逆时针旋转90°,得到△DEF ,DE 交边AC 于G . (1)用含有t 的式子填空:DP ＝ ,AG ＝ ; (2)如图2,当F 在AB 上时,求证:PG ＝PC ;(3)如图3,当P 为DF 的中点时,求AG ∶PG 的值.图1GP FEDCBA图2AC BEFPG D图3A GDP CBFE22.如图1,⊙P 的直径AB 的长为16,E 为半圆的中点,F 为劣弧EB 上的一动点,EF 和AB 的延长线交于C ,过C 作AB 的垂线交AF 的延长线于点D . (1)求证:BC ＝DC ;(2)以直线AB 为x 轴,线段PB 的中垂线为y 轴,建立如图2所示的平面直角坐标系xOy ,则点B 的坐标为(4,0). 设点D 的坐标为(m ,n ),若m ,n 是方程082=+++p px x 的两根,求p 的值;(3)在(2)中的坐标系中,直线8+=kx y 上存在点H ,使△ABH 为直角三角形,若这样的H 点有且只有两个,请直接写出符合条件的k 的值或取值范围.CB ADEP F图1yx 图2FO P E DA B C yxB A EP O 备用图23.如图,抛物线与x 轴交于A(-2,0),B(6,0)两点,与y 轴交于点C(0,-4). (1)求抛物线的解析式;(2)点M 是线段AB 上的一个动点,过点M 作MN∥BC,交AC 于点N,连接CM,当△CMN 的面积最大时,求点M 的坐标;(3)点D(4,k)在(1)中抛物线上,点F 为抛物线上一动点,在y 轴上是否存在点E,使以A 、D 、E 、F 为顶点的四边形是平行四边形?如果存在,求出所有满足条件的点F 的坐标;若不存在,请说明理由.（本题12分）已知如图1，在以O 为原点的平面直角坐标系中，抛物线y ＝41x 2＋bx ＋c 与x 轴交于A 、B 两点，与y 轴交于点C (0，－1)，连接AC ，AO ＝2CO ，直线l 过点G (0，1)且平行于x 轴，t ＜－1(1) 求抛物线对应的二次函数的解析式 (2) 若D 为抛物线y ＝41x 2＋bx ＋c 上一动点，是否存在直线l 使得点D 到直线l 的距离与OD 的长恒相等，若存在，求出此时t 的值(3) 如图2，若E 、F 为上述抛物线上的两个动点，且EF ＝8，线段EF 的中点为M ，求点M 纵坐标的最小值。

武汉市历届元月调考试题分类专题一：数与式1.a 的取值必须满足A.0a ≠B.a ≥2C.a ≠2D.a ≤24．下列函数中，自变量x 的取值范围是x ≥3的函数是（A ）3-=x y （B ）x y -=3（C ）31-=x y （D ）xy -=314.要使式子1x +有意义,x 的取值范围是( ). （A ）x ≥-2 （B ）x ≠-1 （C ）x ≥-2且x ≠-1 （D ）x ≥-12.下列运算不正确的是4=5-110= D.(218=1．化简9的结果是 （A ）3 （B ）－3 （C ）±3 （D ）93.下列等式成立的是( ).（A （B（C ）=（D ）215.观察下列各式的规律：①③.若则a =___________________. 13．计算下面几个式子，它们的结果呈现出一定的规律：1999+⨯、1999999+⨯、1999999999+⨯、1999999999999+⨯．用你发现的规律直接写出式子9999991999999个个个n n n +⨯的结果是 ．13观察你计算的结果，用= .18.先化简,再求值:3x =. 18．一个三角形的三边长分别为55x 、x 2021、xx 5445． （1）求它的周长（要求结果化简）；（2）请你给一个适当的x 值，使它的周长为整数,并求出此时三角形周长的值．武汉市历届元月调考试题分类专题二：方程与不等式3.如果2是方程20x c -=的一个根，那么c 的值是A.4B.-4C.2D.-23．一元二次方程0)3(=+x x 的根为（A ）0 （B ）3 （C ）0或3 （D ）0或－35．如果x ＝3是一元二次方程ax 2＝c 的一个根，那么该方程另一根是（A ）3 （B ）－3 （C ）0 （D ）11.一元二次方程20x x -=的根为( ).（A ）0或1 （B ）±1 （C ）0或-1 （D ）11. 一元二次方程x 2=x 的根是(A) x =1． (B) x =0． (C) x =±1． (D) x 1=0, x 2=1．3.下列方程中，没有实数根的是(A) x 2-x +1=0． (B)3x 2-2x -4=0．(C) x 2-3x =0． (D) x 2+2x +1=0．9.2008年10月29日，央行宣布，从10月30日起下调金融机构人民币存款基准利率.其中一年期存款基准利率由现行的3.87%下调至3.60%.11月26日，央行宣布，从11月27日,一年期存款基准利率由现行的 3.60%下调至2.52%.短短一个月,连续两次降息.设平均每次存款基准利率下调的百分率为x ,根据以上信息可列方程A.3.87% 2.52%2x -=B.()23.871 2.52x -=C.()23.87%1% 1.52%x -=D.()22.52%1 3.87%x +=16.为了让国人分享“神七”升空的骄傲，中央电视台在神七发射期间与“问问”网站联合举办“神七我问问”的活动，网友可以自由地提出问题，解答问题，对问题的解答发表评论。

2023九年级新动力数学元月调考针对训练真题及答案人教版2023年正式开学以来，全国各地九年级学生都迎来了新版数学教材——新动力数学。

为了更好地掌握课程内容，落实教学工作，提高数学基础能力，九年级老师们在课上特意安排元月调考，以便检测学生们对新动力数学知识点的掌握情况。

该次元月调考涉及人教版新动力数学九年级上册有关第六章“方程与不等式”和第七章“二次函数”的知识点，题型包括选择题、填空题、解答题等，共计50分：一、选择题（本大题共10小题，每小题2分，共20分）1.若集合M={2a，3b，c/d}，set N={1/2, -m,-2/a }，则（）A. 集合M∪N={2a，3b，c/d,-m,-2/a }B. 集合M∩N={1/2}C. 集合M-N={2a，3b，c/d}D. 集合N-M={-m,-2/a}2.在φ：y=-2x2+8x-6 定义域内，φ(-1)=-4，求σ：y=(x-2)2+2 的定义域A. (1,3)B. (-3,-1)C. (1,+∞)D. (-∞,3)3.以下方程正确的有（）A. 2x2-10x+7=0B. x2-10x-7=0C. x2-6x+2=0D. 2x2-x+7=04.若一个二次函数为y=2x2+3x－5，则它的最小值是（）A. 5B. -5C. -3D. 0二、填空题（共6小题，每小题2分，共12分）5. 已知 x2 + 4ax + 2a2 =0，a≠0, 则a的值为 ______ 。

6. 设a>0,b>0,且a2+b2=2ab，（a-2b）2的值为____ 。

7.请根据以下二次函数的图象，求出y=2x2-6x-5的解析式。

（图）y=______ 。

三、解答题（共4小题，每小题6分，共24分）8.(本小题满分6分)设y=(2x+1)(x+3)(x-1)，则y=0时，x的值为_______。

9.(本小题满分6分)已知y=2x2+5x-6，求此函数的最大值及极大值点是（）。

２０２２~２０２３学年度高三元月调考数学试卷参考答案一㊁选择题:１．C ㊀㊀２．A㊀㊀３．C ㊀㊀４．B ㊀㊀５．D㊀㊀６．A㊀㊀７．C ㊀㊀８．A 二㊁选择题:９．A C ㊀㊀１０．A B C ㊀㊀１１．A D㊀㊀１２．A B D 三㊁填空题:１３．－６００㊀㊀１４．１２＋８２㊀㊀１５．１６３９㊀㊀１６．１３或１０四㊁解答题:１７．解ʒ(１)c o s (A －C )－c o s B ＝１２⇒c o s (A －C )＋c o s (A ＋C )＝１２⇒c o s A c o s C ＝１４．㊀㊀①又b ２＝a c ,则s i n ２B ＝s i n A s i n C ㊀㊀②故１４－s i n ２B ＝c o s A c o s C －s i n A s i n C ＝c o s (A ＋C )＝－c o s B ⇒４c o s ２B ＋４c o s B －３＝０⇒c o s B ＝１２或c o s B ＝－３２(舍去)．又０＜øB ＜π２,从而,øB ＝π３．(２)由(１)结论,①＋②得c o s (A －C )＝１４＋s i n ２B ＝１则øA ＝øC ．故әA B C 为等边三角形．设әA B C 的边长为x ．则０＜x ＜５．故A C ң C D ＝ң|A C ң||C D ң|c o s ６０ʎ＝１２x (５－x )＝－１２x －５２æèçöø÷２－２５４æèçöø÷ɪ０,２５８æèçùûúú,当且仅当x ＝５２时,上式等号成立．故A C ң C D ң的取值范围是０,２５８æèçùûúú．１８．解ʒ(１)由题意知a n ＞０,因为a n ＋１＝(２－１)a n a n ＋１＋２a n ,所以(a n ＋１＋a n )(a n ＋１－２a n )＝０．因为a n ＞０,所以a n ＋１＋a n ʂ０,所以a n ＋１－２a n ＝０,所以a n ＋１a n ＝２,即a n ＋１a n＝２,１所以{a n }是以１为首项,２为公比的等比数列,所以a n ＝２n －１(n ɪN ∗)．设数列b n {}公差为d ,则１b １b ２＋１b ２b ３＋ １b m －１b m ＝ðm －１i ＝１b i ＋１－b i d b i b i ＋１＝１d ðm －１i ＝１(１b i －１b i ＋１)＝１d (１b １－１b m )＝３㊀㊀ʑd ＝１６,b n ＝n ＋５６．(２)因为C n ＝６b n ＋b １９－a ５＝n －７,所以C n ＝７－n ,n ɤ７,n －７,n ＞７,{所以当n ɤ７时,数列{c n }的前n 项和S n ＝１３n －n ２２;当n ＞７时,数列{c n }的前n 项和S n ＝n ２－１３n ＋８４２．１９．解ʒ(１)P (X ＝３)＝１６æèçöø÷３＝１２１６,当k 次才停止时,必有第k 次取出的是红球,前k －１中有２次取出红球,k －３次取出的是其它颜色球．所以P X ＝k ()＝１６C ２k －１１６æèçöø÷２５６æèçöø÷k －３＝(k －１)(k －２) ５k －３２ ６k ,k ȡ３．(２)当Y ＝４时,有X ＝３,４,故?P Y ＝４()＝P X ＝３()＋P X ＝４()＝１２１６＋５４３２＝７４３２当Y ＝５时,有X ȡ５,故P Y ＝５()＝P X ȡ５()＝１－P X ＝３()＋P X ＝４()()＝４２５４３２于是可得E Y ()＝４P Y ＝４()＋５P Y ＝５()＝２１５３４３２．２０．解ʒ(１)在四边形A E B F 中,ȵәA B E 和әA B F 均为等腰直角三角形,且øB A E ＝øA F B ＝９０ʎ,ʑøB A F ＝øA B E ＝４５ʎ,ʑA F ʊB E ,ȵ四边形A B C D 为正方形,ʑD A ʅA B ,又ȵ平面A B C D ʅ平面A E B F ,D A ⊂平面A B C D ,平面A B C D ɘ平面A E B F ＝A B ,ʑD A ʅ平面A E B F ,V ＝V E －A B C D ＋V F －A B C D ＝４(２)如图建立空间直角坐标系,２设P ０,λ,２－λ(),则B ２,０,０(),C ２,０,２(),F １,－１,０(),A ０,０,０(),ʑB C ң＝０,０,２(),B F ң＝－１,－１,０(),设平面B C F 的一个法向量为n ң＝x ,y ,z (),则n ң B C ң＝０n ң B F ң＝０ìîíïïï,即２z ＝０－x －y ＝０{,令x ＝１,则n ң＝１,－１,０(),设A P 与平面B C F 所成角为θ,又A P ң＝０,λ,２－λ(),ʑs i n θ＝n ң A P ңn ңA P ң＝－λ２λ２＋２－λ()２＝２２ λ２λ２－４λ＋４,要使s i n θ最大,λʂ０,ʑs i n θ＝λ２２λ２－４λ＋４＝２２１４λ２－４λ＋２＝２２ １４１λ－１２æèçöø÷２＋１ɤ２２,ʑθɤπ４,即A P 与平面B C F 所成角的最大值为π４．２１．解ʒ(１)x ２９＋y ２５＝１(２)设点M (x １,y １),N (x ２,y ２),P (x P ,y P ),Q (x Q ,y Q ),F １(－２,０),F ２(２,０),则x ２１a ２＋y ２１b ２＝１,x ２２a ２＋y ２２b２＝１,由于M ,N ,F １三点共线,则y １x １＋２＝y ２x ２＋２⇒x １y ２－x ２y １＝２(y １－y ２),直线MD 的方程为y ＝y １x １－１(x －１),联立椭圆C ʒx ２a ２＋y ２b ２＝１(a ＞b ＞０)的方程可得:x ２a ２＋y ２１b ２(x －１)２(x １－１)２＝１,３化简有ʒ(a ２＋１－２x １)x ２－２(a ２－x ２１)x ＋２a ２x １－(a ２＋１)x ２１＝０,由韦达定理可知ʒx １x P ＝２a ２x １－(a ２＋１)x ２１a ２＋１－２x １⇒x P ＝２a ２－(a ２＋１)x １a ２＋１－２x １,⇒y P ＝y １x １－１２a ２－(a ２＋１)x １a ２＋１－２x １－１æèçöø÷＝(１－a ２)y １a ２＋１－２x １,同理x Q ＝２a ２－(a ２＋１)x ２a ２＋１－２x ２,y Q ＝(１－a ２)y ２a ２＋１－２x ２,k ２＝y P －y Q x P －x Q ＝y １(１－a ２)(a ２＋１－２x ２)－y ２(１－a ２)(a ２＋１－２x １)(a ２＋１－２x ２)(２a ２－(a ２＋１)x １)－(a ２＋１－２x １)(２a ２－(a ２＋１)x ２)＝(a ４－１)(y ２－y １)－２(a ２－１)(x １y ２－x ２y １)(a ２－１)２(x ２－x １)＝a ２＋５a ２－１y ２－y １x ２－x １＝a ２＋５a ２－１k １,从而f (a )＝k ２k １＝a ２＋５a ２－１,由于a ２ɪ(４,＋ɕ),则f (a )ɪ(１,３)．㊀综上ʒf (a )＝a ２＋５a ２－１,且值域为(１,３)．２２．解:(１)f (x )ɤ０,ʑ(x ＋２)l n (x ＋２)ɤ(x ＋１－a )(x ＋２),ʑl n (x ＋２)ɤx ＋１－a ʑa ɤx ＋１－l n (x ＋２)设h (x )＝x ＋１－l n (x ＋２),h ᶄ(x )＝x ＋１x ＋２当(－２,－１)时,h ᶄ(x )＜０,当(－１,＋¥)时,h ᶄ(x )＞０h (x )m i n ＝h (－１)＝０,ʑa ɤ０(２)由(１),知x ＋１＞l n (x ＋２),则l n x ɤx －１,l n a k ɤa k －１,b k l n a k ɤa k b k －b k ,l n a k b k ɤa k b k －b kðn k ＝１l n a k b k ɤðnk ＝１a k b k －ðn k ＝１b k ㊀㊀㊀㊀l n a １b １a ２b ２ a n b n ɤ０,a １b １a ２b ２ a n b n ɤ１． ４。

2021年武汉市初三数学元月调考数学模拟练习试卷一、选择题（共10小题，每小题3分，共30分）1．将方程2326x x -=化为一般形式，若二次项系数为3，则一次项系数和常数项分别为( ) A ．2-，6B ．2-，6-C ．2，6D ．2，6-2．下面四个图形，是中心对称图形的是( )A ．B ．C ．D ．3．关于方程2240x x +-=的根的情况，下列结论错误的是( ) A ．有两个不相等的实数根 B ．两实数根的和为2C ．两实数根的差为25±D ．两实数根的积为4-4．抛掷一枚质地均匀的硬币，正面朝上的概率为0.5，下列说法正确的是( ) A ．连续抛掷2次必有1次正面朝上 B ．连续抛掷10次不可能都正面朝上 C ．大量反复抛掷每100次出现正面朝上50次 D ．通过抛掷硬币确定谁先发球的比赛规则是公平的5．如图，AB 为O 的直径，CD 为O 的弦，AB CD ⊥于E ，下列说法错误的是( )A ．CE DE =B ．AC AD =C ．OE BE =D ．2COB BAD ∠=∠6．圆的直径是13cm ，如果圆心与直线上某一点的距离是6.5cm ，那么该直线和圆的位置关系是( ) A ．相离B ．相切C ．相交D ．相交或相切7．如图，Rt ABC ∆中，90C ∠=︒，3BC =，4AC =，将ABC ∆绕点B 逆时针旋转得△A BC ''，若点C '在AB 上，则AA '的长为( )A ．13B ．4C ．25D ．58．若m ，n 为方程2310x x --=的两根，则多项式23m n +的值为( ) A ．8-B ．9-C ．9D ．109．如图，分别以等边三角形ABC 的三个顶点为圆心，以边长为半径画弧，得到的封闭图形是莱洛三角形，若2AB =，则莱洛三角形的面积（即阴影部分面积）为( )A ．3π+B ．3π-C ．23π-D ．223π-10．若方程220x x t --=在14x -<范围内有实数根，则t 的取值范围为( ) A ．38t <B ．13t -C ．18t -<D ．18t -二、填空题（共6小题，每小题3分，共18分） 11．若2是方程20x c -=的一个根，则c 的值为 ．12．把抛物线22y x =先向下平移1个单位，再向左平移2个单位，得到的抛物线的解析式是 ． 13．如图，四边形ABCD 内接于O ，110A ∠=︒，则BOD ∠= ︒．14．有不同的两把锁和三把钥匙，其中两把钥匙能分别打开这两把锁，第三把钥匙不能打开这两把锁．任意取出一把钥匙去开任意的一把锁，一次打开锁的概率是 ．15．二次函数2(y ax bx c a =++、b 、c 为常数，0)a ≠中的x 与y 的部分对应值如表：x1-0 3 yn3-3-当0n >时，下列结论中一定正确的是 ．（填序号即可）①0bc >；②当2x >时，y 的值随x 值的增大而增大；③4n a >；④当1n =时，关于x 的一元二次方程2(1)0ax b x c +++=的解是11x =-，23x =．16．如图，AB 为O 的直径，C 为O 上一动点，将AC 绕点A 逆时针旋转120︒得AD ，若2AB =，则BD 的最大值为 ．三、解答题17．已知关于x 的方程2(2)210x m x m +++-=，当m 为何值时，方程的两根相互为相反数？并求出此时方程的解．18．如图，在O 中，弦AB 与弦CD 相交于点E ，且AB CD =．求证：CE BE =．19．把一副普通扑克牌中的4张：黑2，红3，梅4，方5，洗匀后正面朝下放在桌面上． （1）从中随机抽取一张牌是红心的概率是 ；（2）从中随机抽取一张，再从剩下的牌中随机抽取另一张．请用表格或树状图表示抽取的两张牌牌面数字所有可能出现的结果，并求抽取的两张牌牌面数字之和大于7的概率．20．如图，在下列的网格中，横、纵坐标均为整数的点叫做格点，例如(3,0)A ，(0,4)B ，(4,2)C 都是格点． （1）直接写出ABC ∆的形状；（2）要求在上图中仅用无刻度的直尺作图：将ABC ∆绕点B 逆时针旋转得到△11A BC ，旋转角2ABC =∠，请你完成作图；（3）在网格中找一个格点G ，使得1C G AB ⊥，并直接写出G 点坐标．21．如图，O 是ABC ∆的外心，I 是ABC ∆的内心，连AI 并延长交BC 和O 于D 、E 两点． （1）求证：EB EI =；（2）若4AB =，3AC =，2BE =，求AI 的长．22．某公司销售一种商品，成本为每件20元，经过市场调查发现，该商品的日销售量y （件)与销售单价x （元)是一次函数关系，其销售单价、日销售量的三组对应数值如下表：销售单价x （元) 40 60 80 日销售量y （件) 806040（1）求y 与x 的关系式；（2）若物价部门规定每件商品的利润率不得超过100%，求公司销售该商品获得的最大日利润； （3）若物价部门规定该商品销售单价不能超过a 元，并且由于某种原因，该商品每件成本变成了之前的2倍，在日销售量y （件)与销售单价x （元)保持（1）中函数关系不变的情况下，该商品的日销售最大利润是1500元，求a 的值．23．如图，在ABC ∆中，AB AC =，120BAC ∠=︒，D 为BC 边上的点，将DA 绕D 逆时针旋转120︒得到DE ． （1）如图1，若30DAC ∠=︒． ①求证：AB BE =；②直接写出22BE CD +与2AD 的数量关系为 ；（2）如图2，D 为BC 边上任意一点，线段BE 、CD 、AD 是否满足（1）中②的关系，请给出结论并证明．24．抛物线2y ax ax b =-+交x 轴于A ，B 两点(A 在B 的左边），交y 轴于C ，直线4y x =-+经过B ，C 两点．（1）求抛物线的解析式；（2）如图1，P 为直线BC 上方的抛物线上一点，//PD y 轴交BC 于D 点，过点D 作DE AC ⊥于E 点．设1021m PD DE =+，求m 的最大值及此时P 点坐标； （3）如图2，点N 在y 轴负半轴上，点A 绕点N 顺时针旋转，恰好落在第四象限的抛物线上点M 处，且180ANM ACM ∠+∠=︒，求N 点坐标．参考答案与试题解析一、选择题（共10小题，每小题3分，共30分）1．解：由2326x x -=，得23260x x --=，所以一次项系数是2-、常数项是6-， 故选：B ．2．解：A 、不是中心对称图形，故本选项不合题意；B 、不是中心对称图形，故本选项不合题意；C 、不是中心对称图形，故本选项不合题意；D 、是中心对称图形，故本选项符合题意．故选：D ．3．解：方程2240x x +-=， 这里1a =，2b =，4c =-， △416200=+=>，∴方程有两个不相等的实数根，且122x x +=-，124x x =-，12x x ∴-==±故结论错误的是B ， 故选：C ．4．解：抛掷一枚质地均匀的硬币，正面朝上的概率为0.5，可以用到实际生活，通过抛掷硬币确定谁先发球的比赛规则是公平的． 故选：D ．5．解：连接OD ，如图， AB CD ⊥，CE DE ∴=，AC AD =，BC BD =， BC BD =，BOC BOD ∴∠=∠， 2BOD BAD ∠=∠， 2BOC BAD ∴∠=∠．故选：C ．6．解：圆的直径为13 cm ，∴圆的半径为6.5 cm ，圆心与直线上某一点的距离是6.5cm ，∴圆的半径圆心到直线的距离，∴直线于圆相切或相交，故选：D ．7．解：根据旋转可知：90AC B C ∠''=∠=︒，4AC AC ''==，AB A B ='，根据勾股定理，得2222345AB BC AC ++=， 5A B AB ∴'==， 2AC AB BC ∴'=-'=，在Rt △AA C ''中，根据勾股定理，得22222425AA AC A C ''''=++ 故选：C ．8．解：m ，n 为方程2310x x --=的两根， 2310m m ∴--=，3m n +=， 231m m ∴-=．22333313()13310m n m m m n m n ∴+=-++=++=+⨯=． 故选：D ．9．解：过A 作AD BC ⊥于D ，ABC ∆是等边三角形，2AB AC BC ∴===，60BAC ABC ACB ∠=∠=∠=︒， AD BC ⊥，1BD CD ∴==，33AD BD ==ABC ∴∆的面积为1123322BC AD ⨯⨯=⨯260223603BACS ππ⨯==扇形，∴莱洛三角形的面积23232233S ππ=⨯-=-故选：D ．10．解：设212y x x =-，212y x x =-的对称轴为直线1x =，∴一元二次方程220x x t --=的实数根可以看作212y x x =-与函数2y t =的交点，方程在14x -<的范围内有实数根， 当1x =-时，13y =； 当4x =时，18y =；函数212y x x =-在1x =时有最小值1-；∴当18t -时，212y x x =-与函数2y t =有交点，即方程220x x t --=在18t -<范围内有实数根；故选：D ．二、填空题（共6小题，每小题3分，共18分）11．解：根据题意，将2x =代入方程20x c -=，得：40c -=， 解得4c =， 故答案为：4．12．解：由“上加下减”的原则可知，二次函数22y x =的图象向下平移1个单位得到221y x =-， 由“左加右减”的原则可知，将二次函数221y x =-的图象向左平移2个单位可得到函数22(2)1y x =+-，故答案是：22(2)1y x =+-．13．解：四边形ABCD 内接于O ，110A ∠=︒， 180********C A ∴∠=︒-∠=︒-︒=︒， 2140BOD C ∴∠=∠=︒．故答案为：140．14．解：画树状图为：（两把钥匙能分别打开这两把锁表示为A 、a 和B 、b ，第三把钥匙表示为)c共有6种等可能的结果数，其中任意取出一把钥匙去开任意的一把锁，一次打开锁的结果数为2， 所以任意取出一把钥匙去开任意的一把锁，一次打开锁的概率2163==． 故答案为13．15．解：①函数的对称轴为直线13(03)22x =+=，即322b a =-，则3b a =-，0n >，故在对称轴的左侧，y 随x 的增大而减小，故抛物线开口向上，则0a >，对称轴在y 轴的右侧，故0b <，而3c =-，故0bc >正确，符合题意；②2x =在函数对称轴的右侧，故y 的值随x 值的增大而增大，故②正确，符合题意； ③当1x =-时，434n y a b c a a ==-+=-<，故③错误，不符合题意； ④当1n =时，即：1x =-时，1y =，2(1)0ax b x c +++=可以变形为2ax bx c x ++=-，即探讨一次函数y x =-与二次函数为2y ax bx c =++图象情况，当1x =-，1y =，即(1,1)-是上述两个图象的交点，则抛物线和另一个交点在第四象限，且横纵坐标互为相反数，而本题表中告诉了(3,3)-在二次函数图象上，所以另一个交点为(3,3)-， 故两个函数交点的横坐标为1-、3，即关于x 的一元二次方程2(1)0ax b x c +++=的解是11x =-，23x =，正确，符合题意， 故答案为：①②④．16．解：解法一：如图，将ABD ∆绕点A 顺时针旋转120︒，则D 与C 重合，B '是定点，BD 的最大值即B C '的最大值，即B '、O 、C 三点共线时，BD 最大，过B '作B E AB '⊥于点E ，由题意得：2AB AB '==，120BAB '∠=︒， 60EAB '∴∠=︒，Rt AEB '∆中，30AB E '∠=︒，112AE AB '∴==，22213EB '=-=， 由勾股定理得：22222(3)7OB OE B E ''=+=+=， 71B C OB OC ''∴=+=+．解法二：如图1，连接OC ，将AOC ∆绕点A 逆时针旋转120︒得到AGD ∆，发现点D 的运动轨迹是：以G 为圆心，以AG 为半径的圆，所以当B 、G 、D 三点共线时，BD 的值最大，如图2，过点G 作GH AB ⊥，交BA 的延长线于H ，由旋转得：1AO AG ==，120OAG ∠=︒， 60HAG ∴∠=︒， 30AGH ∴∠=︒，12AH ∴=，3GH由勾股定理得：222231()(2)722BG GH BH =+=++= BD ∴71．故答案为：71+． 三、解答题17．解：关于x 的方程2(2)210x m x m +++-=两根相互为相反数，(2)0m ∴-+=，解得2m =-，则方程为250x -=，解得15x =，25x =-．18．证明：AB CD =，∴AB CD =，∴AB CB CD CB -=-，即AC BD =，C B ∴∠=∠，CE BE ∴=．19．解：（1）从黑2，红3，梅4，方5这4张扑克牌中任摸一张，是红心的可能性为14， 故答案为：14； （2）用列表法表示所有可能出现的结果情况如下：共有12种等可能出现的结果，其中和大于7的有4种，所以抽取的两张牌牌面数字之和大于7的概率为41123=． 20．解：如图所示：（1）ABC ∆的形状为：直角三角形；（2）将ABC ∆绕点B 逆时针旋转得到△11A BC ，旋转角2ABC =∠；（3）在网格中找一个格点G ，使得1C G AB ⊥，G 点坐标为(0,3)．21．（1）证明：I 是ABC ∆的内心，AE ∴平分CAB ∠，BI 平分ABC ∠，BAE CAE ∴∠=∠，ABI CBI ∠=∠，BIE BAE ABI ∠=∠+∠，IBE IBD EBD ∠=∠+∠，CBE CAE ∠=∠，BIE EBI ∴∠=∠，EB EI ∴=；（2）解：连接EC ．BAE CAE ∠=∠，∴BE EC =，2BE EC ∴==，ADB CDE ∠=∠，BAD DCE ∠=∠，ADB CDE ∴∆∆∽， ∴422BD AD AB DE DC EC ====，设DE m =，CD n =，则2BD m =，2AD n =， 同法可证：ADC BDE ∆∆∽， ∴AD AC BD BE =， ∴2322n m =， :3:2n m ∴=，设3n k =，2m k =，CED AEC ∠=∠，ECD BAE CAE ∠=∠=∠，ECD EAC ∴∆∆∽，2EC ED EA ∴=⋅，4(2)m m n ∴=⋅+，42(26)k k k ∴=+ 12k ∴=或12-（舍弃）， 1DE ∴=，3AD =，4AE ∴=，2EI BE ==，2AI AE EI ∴=-=．解法二：过点E 作EM AB ⊥，EN AC ⊥交AC 的延长线于N ．利用全等三角形的性质证明AM AN =，BM CN =，EM EN =，求出BM ，EM ，AE ，可得结论．22．解：（1）设函数的表达式为y kx b =+，将(40,80)、(60,60)代入上式得：40806060k b k b +=⎧⎨+=⎩，解得1120k b =-⎧⎨=⎩， 故y 与x 的关系式为120y x =-+；（2）公司销售该商品获得的最大日利润为w 元， 则2(20)(20)(120)(70)2500w x y x x x =-=--+=--+，200x -，1200x -+，2020100%x -⨯，2040x ∴，10-<，故抛物线开口向下，故当70x <时，w 随x 的增大而增大，∴当40x =（元)时，w 的最大值为1600（元)，故公司销售该商品获得的最大日利润为1600元；（3）当1500w =最大时，2(80)16001500x --+=，解得170x =，290x =，2200x -⨯，40x ∴，又x a ，40x a ∴．∴有两种情况，①80a <时，即40x a ，在对称轴左侧，w 随x 的增大而增大，∴当70x a ==时，1500w =最大，②80a 时，即40x a ，在40x a 范围内16001500w =≠最大，∴这种情况不成立，70a ∴=．23．（1）①证明：如图1中，AB AC =，120BAC ∠=︒30ABC ACB ∴∠=∠=︒，30DAC ∠=︒30DAC ACB ∴∠=∠=︒，60ADB CAD ACB ∠=∠+∠=︒，90BAD ∴∠=︒，由旋转得：DE DA CD ==，60BDE ADB ∠=∠=︒，()BDE BDA SAS ∴∆≅∆，AB BE ∴=．②解：BDE BDA ∆≅∆，90BED BAD ∴∠=∠=︒，BE AB =，22222BE CD BE DE BD ∴+=+= 1cos cos602AD ADB BD =∠=︒=， 2BD AD ∴=，2224BE CD AD ∴+=． 故答案为：2224BE CD AD +=． （2）能满足（1）中的结论．理由：当点E 在BC 的下方时，将ACD ∆绕点A 顺时针旋转120︒得到ABD ∆'，使AC 与AB 重合，连接ED '，DD '，AE ，设AB 交DD '于点J ．30DBJ ADJ ∠=∠=︒，BJD D JA ∠=∠'，BJD ∴∆∽△D JA '，∴BJ DJ D J AJ ='， ∴BJ D J DJ AJ'=， BJD DJA ∠'=∠，BJD DJA ∴∆'∆∽，30JBD JDA ∴∠'=∠=︒，同法可证，30EBD EAD ∠=∠=︒，30ED D EAD ∠'=∠=︒，30ABC D BJ EBD ∠=∠'=∠=︒，90D BE ∴∠'=︒，120ADE ∠=︒，30ADD ∠'=︒，90D DE ∴∠'=︒，30ED D ∠'=︒，22D E DE AD ∴'==，在Rt △D BE '中，222D E D B BE '='+，CD BD ='，2224CD BE AD ∴+=．当B ，E 重合时，0BE =，90DAC ∠=︒，30C ∠=︒，2CD AD ∴=，24CD AD ∴=，结论成立．当点E 在BC 的上方时，如图3中，同法可证，90EBD ∠'=︒，22ED AD AD '='=．222BD BE ED ∴'+='，2224CD BE AD ∴+=．24．解：（1）当0x =时，4y =；当0y =时，40x -+=，4x =；(4,0)B ∴，(0,4)C ，点B ，C 在抛物线上，∴16404a a b b -+=⎧⎨=⎩，解得：134a b ⎧=-⎪⎨⎪=⎩， 211433y x x ∴=-++； （2）如图1，连接AD ，延长PD 交x 轴于H ，//PD y 轴，PH x ∴⊥轴，设(,4)D t t -+，211(,4)33P t t t -++， 2211144(4)3333PD t t t t t =-++--+=-+， ABC ADC ADB S S S ∆∆∆=+，且(3,0)A -，(4,0)B ，(0,4)C ， ∴111747(4)222AC DE t ⨯⨯=⋅+⨯⨯-+， 22345AC =+，75DE t ∴=， 1021m PD DE =+， 22214107112(3)33321533m t t t t t t ∴=-++⋅=-+=--+， ∴当3t =时，m 有最大值是3，此时(3,2)P ；（3）过N 作NF MC ⊥交MC 于点F ，过N 点作NG AC ⊥，交CA 的延长线于点G ，则90G CFN ∠=∠=︒， 180ACM GNF ∴∠+∠=︒，由旋转得：AN MN =， 180ANM ACM ∠+∠=︒， ANM GNF ∴∠=∠， ANG MNF ∴∠=∠， 90G MFN ∠=∠=︒， ()NGA NFM AAS ∴∆≅∆， NG NF ∴=，NC ∴平分ACM ∠， CO AB ⊥，3OK OA ∴==， (3,0)K ∴，CK ∴的解析式为：443y x =-+， 241144333x x x ∴-+=-++， 解得：10x =，25x =，8(5,)3M ∴-， 设(0,)N y ，AN MN =，22228(3)5()3y y ∴-+=++，解得：133y =-， 13(0,)3N ∴-．。

2024届湖北省十堰市高三上学期元月调研考试物理高频考点试卷一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题如图所示，OB是竖直线，OA是水平线，B与O的距离为h（可调节），A与O的距离为x（x为定值）。

小球在B点以合适的速度水平抛出，每次都能击中水平面上的A点，不计空气阻力，则（ ）A．h越大，小球水平抛出的速度越大B．h越大，击中A点时速度与竖直方向夹角越大C．h越大，击中A点时重力的瞬时功率越大D．当时，击中A点的动能最小第(2)题如图（a）为一列简谐横波在t=0.5s时刻的波形图，介质中的两个质点P、Q此刻离开平衡位置的位移分别为0.5A、，图（b）是质点Q的振动图像。

下列说法正确的是（ ）A．波沿方向传播，0.5s时刻P质点正在向方向振动B．波沿方向传播，0.5s时刻P质点正在向方向振动C．波速为2cm/s，P、Q振动方向有时相同有时相反D．波速为4cm/s，0.5s时刻质点P在加速、质点Q在减速第(3)题一列简谐波在时波的图像如图甲所示，处的质点的振动图像如图乙所示，由此可知（ ）A．波沿x轴负方向传播B．波速C．时刻，质点a向y轴正方向运动D．时刻，质点b的位移第(4)题图1和图2是教材中演示自感现象的两个电路图，和为电感线圈。

实验时，断开开关瞬间，灯突然闪亮，随后逐渐变暗；闭合开关，灯逐渐变亮，而另一个相同的灯立即变亮，最终与的亮度相同。

下列说法正确的是（ ）A．图1中，与的电阻值相同B．图1中，闭合开关，灯逐渐变亮C．图2中，变阻器R与的电阻值相同D．图2中，断开瞬间，灯突然闪亮第(5)题图左侧为不锈钢砧板架实物图。

在图右侧图中，质量为M的圆形砧板稳稳的竖立在砧板架上，砧板架两侧横梁近似光滑，间距为d，取重力加速度为g，下列说法正确的是（ ）A．砧板对砧板架一侧横梁的作用力一定小于M gB．若增大横梁的间距d，砧板对两侧横梁的作用力均增大C．若增大横梁的间距d，砧板架对地面的压力增大D．若换一个质量相同直径更大的砧板，两侧横梁受到的压力均增大第(6)题如图所示为氢原子的能级图，已知可见光的光子能量范围为，锌的逸出功为3.34eV，下列说法正确的是（ ）A．氢原子由激发态跃迁到基态后，核外电子的动能减小，原子的电势能增大B．处于能级的氢原子可以吸收任意频率的紫外线，并且使氢原子电离C．一个处于能级的氢原子向低能级跃迁时，最多发出6种不同频率的光子D．一群处于能级的氢原子向基态跃迁时，发出的光照射锌板，锌板表面所发出的光电子的最大初动能为8.75eV第(7)题静电喷漆技术具有效率高，浪费少，质量好，又利于工人健康等优点，其简化原理如图所示。