spss教程均值比较检验与方差分析
- 格式:doc
- 大小:411.00 KB
- 文档页数:19
如何利用SPSS计算平均值,标准差,单因素方差单因素方差用于分析单一控制变量影响下的多组样本的均值是否存在显著差异。
在进行方差分析时要求样本满足以下几个条件:(1)可比性;(2)随机数据;(3)样本为正态分布;(4)方差齐性,要求各组间具有相同的方差,可以通过SPSS中“方差齐性检验”得出。
下面以医学中不同类型脑梗塞与年龄、性别和ApoB/AI值之间的相互关系来进行单因素方差分析。
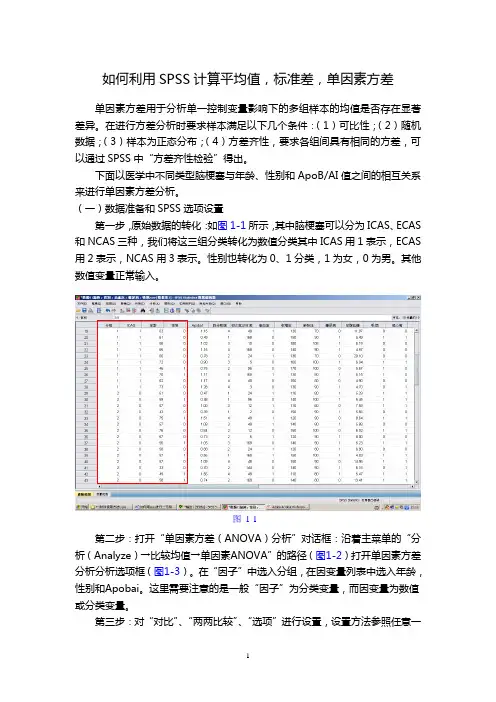
(一)数据准备和SPSS选项设置第一步,原始数据的转化:如图1-1所示,其中脑梗塞可以分为ICAS、ECAS 和NCAS三种,我们将这三组分类转化为数值分类其中ICAS用1表示,ECAS 用2表示,NCAS用3表示。
性别也转化为0、1分类,1为女,0为男。
其他数值变量正常输入。
图1-1第二步:打开“单因素方差(ANOVA)分析”对话框:沿着主菜单的“分析(Analyze)→比较均值→单因素ANOVA”的路径(图1-2)打开单因素方差分析分析选项框(图1-3)。
在“因子”中选入分组,在因变量列表中选入年龄,性别和Apobai。
这里需要注意的是一般“因子”为分类变量,而因变量为数值或分类变量。
第三步:对“对比”、“两两比较”、“选项”进行设置,设置方法参照任意一本SPSS统计书籍中关于单因素方差分析的部分。
图1-2图1-3点击确定后输出数据,这里重点讲输出数据中各项所代表的意思。
我们经常会在其他文献中看到有关平均值(mean),标准差(SD)和标准误差(SE),即mean±SD或SE的情况。
如图1-4所示“描述图”中,在该图中我们很容易找到以上几项。
如图1-4所示“方差齐性检验”中,我们可以找到各组的显著性(即P值),也有软件表示为Sig.。
当该值大于0.05时说明各组间方差是齐性的,既满足前提的第四点。
可以进行后续分析。
一般我们需要的是多重比较的表格,如图1-5所示,该表中给出了年龄、性别和ApoB/AI值中各组间的显著性水平(P值),如年龄组中1、2组间显著性为0.972,差异不显著。








SPSS数据的参数检验和方差分析SPSS软件是一种用于统计和数据分析的工具,它可以进行各种参数检验和方差分析。
本文将重点介绍SPSS中的参数检验和方差分析,并提供一些建议和注意事项。
参数检验是一种统计方法,用于确定一个或多个总体参数的真实值。
在SPSS中,可以使用各种统计方法进行参数检验,例如t检验、方差分析(ANOVA)、卡方检验等。
t检验是用于比较两个样本均值是否显著不同的方法。
在SPSS中,可以通过选择“分析”->“比较均值”->“独立样本t检验”或“相关样本t检验”来执行t检验。
在进行t检验之前,需要确保数据符合正态分布和方差齐性的假设。
可以使用SPSS中的正态性检验和方差齐性检验来验证这些假设。
方差分析是用于比较三个或更多组之间差异的方法。
在SPSS中,可以通过选择“分析”->“方差”->“单因素方差分析”或“多因素方差分析”来执行方差分析。
在进行方差分析之前,同样需要检验正态性和方差齐性的假设。
在进行参数检验和方差分析时,还需确认是否使用方差分析的正确方法。
例如,如果有多个自变量,可能需要使用混合设计方差分析或多重方差分析等方法。
SPSS提供了多种不同的方差分析方法,可以根据具体研究设计选择适当的方法。
进行参数检验和方差分析时,还需要注意一些统计概念和报告结果的规范。
例如,结果中应包括样本均值、标准差、置信区间、显著性水平等信息。
此外,还应使用适当的图表和图形来展示数据和结果,以帮助读者更好地理解研究结果。
除了参数检验和方差分析,SPSS还可以进行其他类型的统计分析,例如相关分析、回归分析、因子分析等。
这些分析方法可以用来探索和描述数据之间的关系,以及预测和解释变量之间的关系。
在使用SPSS进行数据分析时,还需注意数据的质量和准确性。
确保数据输入正确、完整,处理缺失值和异常值等。
此外,也需要根据研究目的和问题选择合适的统计方法,并理解相关假设和前提条件。
总之,SPSS是一种功能强大的统计和数据分析工具,在参数检验和方差分析方面提供了丰富的方法和功能。


均值检验、方差分析SPSS以下是为大家整理的均值检验、方差分析spss的相关范文,本文关键词为均值,检验,方差,分析,spss,实验,目的,要求,spss,您可以从右上方搜索框检索更多相关文章,如果您觉得有用,请继续关注我们并推荐给您的好友,您可以在综合文库中查看更多范文。
一、实验目的及要求:1、目的用spss软件实现均值检验和方差分析。
2、内容及要求用spss对所要求数据进行相应的数据处理和分析:均值检验、方差分析。
二、仪器用具:仪器名称计算机spss软件规格/型号数量11备注有网络环境三、实验方法与步骤:1.从网上下载到可用的数据2.将所需数据复制到spss中,并且把学校变量改为数值型变量,用1、2分别代替“A”和“b”。
四、实验结果与数据处理:首先用spss软件对单变量进行正态性检验,结果如下:正态性检验Kolmogorov-smirnova统计量语文数学英语物理化学.084.102.071.087.073df6060606060sig..200*.192.200.200*.200**sha piro-wilk统计量.986.972.982.990.984df6060606060sig..698.185.512.894.627a.Lilliefo rs显著水平修正*.这是真实显著水平的下限。
因为样本数n=60用spss的gLm模块进行多元正态分布有关均值与方差的检验,结果如下:1第一张主体间因子表展示了样本数据分别来自两个学校的个数。
第二张多变量检验表给出了几个统计量,由sig.值可以看出,无论从哪个统计量来看,两个学校的录取分数都是有显著差别的。
由于模型通过了显著性检验,意味着两所学校的录取分数线是不同的。
主体间因子学校Abn3030多变量检验b效应截距pillai的跟踪wilks的Lambdahotelling的跟踪Roy的最大根学校pillai的跟踪wilks的Lambdahotelling的跟踪Roy的最大根 a.精确统计量 b.设计:截距+学校值.999.0011554.6561554.656.851.1495.7105.710F16790.281a16790.28 1a16790.281a16790.281a61.672a61.672a61.672a61.672a假设df5.0005.0005.0005.0005.0005.0005.0005.000误差df54.00054.00054.00054.00054.00054.00054.00054.000sig..000.000.00 0.000.000.000.000.000主体间效应的检验源校正模型因变量语文数学英语物理化学截距语文数学英语物理化学学校语文数学英语物理III 型平方和1050.017a1470.150b1135.350c1859.267d1560.600e372408.817376833. 750388010.417389781.600383360.2671050.0171470.1501135.3501859. 267df11111111111111均方1050.0171470.1501135.3501859.2671560.600372408.817376833.75038 8010.417389781.600383360.2671050.0171470.1501135.3501859.267F4 8.25186.03439.83183.39241.65217113.20XX2052.62613612.47917482. 60010231.72248.25186.03439.83183.392sig..000.000.000.000.000.000.000.000.000.000.000.000.000.0002化学误差语文数学英语物理化学总计语文数学英语物理化学校正的总计语文数学英语物理化学a.R方=.454(调整R方=.445)b.R方=.597(调整R方=.590)c.R方=.407(调整R方=.397)d.R方=.590(调整R方=.583) e.R方=.418(调整R方=.408)1560.6001262.167991.1001653.2331293.1332173.133374721.00037929 5.000390799.000392934.000387094.0002312.1832461.2502788.583315 2.4003733.73315858585858606060606059595959591560.60021.76117. 08828.50422.29537.46841.652.000由上面主体间效应的检验表可知五科分数的sig.值均为0.000说明两个学校本科录取分数在五门课上都存在显著差别。
第5章SPSS均值比较T检验和方差分析第5章主要介绍了SPSS软件中进行均值比较的方法,包括t检验和方差分析。
本文将详细介绍SPSS中进行均值比较的步骤,以及如何解读结果。
5.1t检验t检验是一种用于比较两个样本均值差异的统计方法。
在SPSS中,进行t检验的步骤如下:1.打开SPSS软件,并导入需要进行t检验的数据集。
2.选择“分析”菜单,在下拉菜单中选择“比较均值”选项,再选择“独立样本t检验”选项。
3.在弹出的对话框中,将需要比较的变量移动到“因子”框中,将“分组变量”移动到“因子”框中,并选择需要进行的假设检验类型。
4.点击“确定”按钮,等待计算结果。
5.在输出窗口中,可以查看计算结果,包括均值、标准差、样本量、t值和p值等。
通常,我们关注的是p值,如果p值小于0.05,则认为差异显著。
例如,我们想比较男性和女性的体重是否有显著差异。
我们将体重作为因变量,性别作为自变量,进行t检验。
在计算结果中,如果p值小于0.05,则可以认为男女性别对体重有显著影响。
5.2方差分析方差分析是一种用于比较三个或更多个样本均值是否存在差异的统计方法。
在SPSS中,进行方差分析的步骤如下:1.打开SPSS软件,并导入需要进行方差分析的数据集。
2.选择“分析”菜单,在下拉菜单中选择“比较均值”选项,再选择“单因素方差分析”选项。
3.在弹出的对话框中,将需要比较的变量移动到“因子”框中,将“分组变量”移动到“因子”框中,并选择需要进行的假设检验类型。
4.点击“确定”按钮,等待计算结果。
5.在输出窗口中,可以查看计算结果,包括均值、标准差、样本量、F值和p值等。
通常,我们关注的是p值,如果p值小于0.05,则认为差异显著。
例如,我们想比较不同药物对治疗效果的影响。
我们将药物作为因变量,治疗效果作为自变量,进行方差分析。
在计算结果中,如果p值小于0.05,则可以认为不同药物对治疗效果有显著影响。
通过以上步骤,我们可以在SPSS中进行均值比较、t检验和方差分析。
第二章均值比较检验与方差分析在经济社会问题的研究过程中,常常需要比较现象之间的某些指标有无显著差异,特别当考察的样本容量n比较大时,由随机变量的中心极限定理知,样本均值近似地服从正态分布。
所以,均值的比较检验主要研究关于正态总体的均值有关的假设是否成立的问题。
◆本章主要内容:1、单个总体均值的 t 检验(One-Sample T Test);2、两个独立总体样本均值的 t 检验(Independent-Sample T Test);3、两个有联系总体均值均值的 t 检验(Paired-Sample T Test);4、单因素方差分析(One-Way ANOVA);5、双因素方差分析(General Linear Model Univariate)。
◆假设条件:研究的数据服从正态分布或近似地服从正态分布。
在Analyze菜单中,均值比较检验可以从菜单Compare Means,和General Linear Model得出。
如图2.1所示。
图2.1 均值的比较菜单选择项§2.1 单个总体的t 检验(One-Sample T Test)分析单个总体的 t 检验分析也称为单一样本的 t 检验分析,也就是检验单个变量的均值是否与假定的均数之间存在差异。
如将单个变量的样本均值与假定的常数相比较,通过检验得出预先的假设是否正确的结论。
例1:根据2002年我国不同行业的工资水平(数据库SY-2),检验国有企业的职工平均年工资收入是否等于10000元,假设数据近似地服从正态分布。
首先建立假设:H0:国有企业工资为10000元;H1:国有企业职工工资不等于10000元打开数据库SY-2,检验过程的操作按照下列步骤:1、单击Analyze →Compare Means →One-Sample T Test,打开One-Sample T Test 主对话框,如图2.2所示。
图2.2 一个样本的t检验的主对话框2、从左边框中选中需要检验的变量(国有单位)进入检验框中。
方差分析/F检验(多个均数比较)前言:一、方差分析的基本思想方差是反映数据变异程度的统计指标。
利用方差的概念对变异度进行分解,所以方差分析亦称为变异度分析。
其基本思想是:根据研究目的和设计类型,将全部观察值的总变异分解为两个或多个部分,各部分的变异可由不同处理因素的影响效应或者误差的效应解释,将各影响因素产生的变异与随机误差变异进行比较,以推断该因素是否存在影响效应。
二、方差分析的应用条件独立性:各样本是相互独立的随机样本,个体观测值之间相互独立。
正态性:各样本均来自正态分布总体。
方差齐性:各样本所对应的总体方差相等。
三、常用的方差齐性检验方法F 检验:仅用于两总体方差相等Bartlett检验:通常要求数据满足正态性Levene检验(Levene‘s teste):不依赖数据的分布类型,结果更稳健四、完全随机设计的方差分析完全随机设计(completely randomized design)的方差分析是指将研究对象通过完全随机化方法,分配至多个不同的处理组,比较多组的效应指标是否存在差别,亦称为单向方差分析(one-way ANOVA)/单因素方差分析。
注:完全随机设计的方差分析只涉及一个研究因素,因此,除了用于随机分组的试验性研究外,也常用于基于随机抽样的观察性研究多个均数的比较。
SPSS正文:一、单因素方差分析(单个因素作用,处理因素——独立正态方差齐):SPSS操作:第一步:建立数据文件(变量:group 和观察值共2列;类似两组独立样本t检验的数据录入);第二步:正态性检验(类似两组独立样本t检验的正态性检验)1、分割文件(data→split file→激活compare groups→调入group→OK);自我经验,此处可有可无,分割和不分割的结果未变化。
2、正态性检验(analyze→nonparametrice tests→1-sample K-S→调入观察值,点击normal→OK)3、观察结果,若三组正态性检验P均>0.05,则进行下一步。
第二章均值比较检验与方差分析在经济社会问题的研究过程中,常常需要比较现象之间的某些指标有无显著差异,特别当考察的样本容量n比较大时,由随机变量的中心极限定理知,样本均值近似地服从正态分布。
所以,均值的比较检验主要研究关于正态总体的均值有关的假设是否成立的问题。
◆本章主要内容:1、单个总体均值的 t 检验(One-Sample T Test);2、两个独立总体样本均值的 t 检验(Independent-Sample T Test);3、两个有联系总体均值均值的 t 检验(Paired-Sample T Test);4、单因素方差分析(One-Way ANOVA);5、双因素方差分析(General Linear Model Univariate)。
◆假设条件:研究的数据服从正态分布或近似地服从正态分布。
在Analyze菜单中,均值比较检验可以从菜单Compare Means,和General Linear Model得出。
如图2.1所示。
图2.1 均值的比较菜单选择项§2.1 单个总体的t 检验(One-Sample T Test)分析单个总体的 t 检验分析也称为单一样本的 t 检验分析,也就是检验单个变量的均值是否与假定的均数之间存在差异。
如将单个变量的样本均值与假定的常数相比较,通过检验得出预先的假设是否正确的结论。
例1:根据2002年我国不同行业的工资水平(数据库SY-2),检验国有企业的职工平均年工资收入是否等于10000元,假设数据近似地服从正态分布。
首先建立假设:H0:国有企业工资为10000元;H1:国有企业职工工资不等于10000元打开数据库SY-2,检验过程的操作按照下列步骤:1、单击Analyze →Compare Means →One-Sample T Test,打开One-Sample T Test 主对话框,如图2.2所示。
图2.2 一个样本的t检验的主对话框2、从左边框中选中需要检验的变量(国有单位)进入检验框中。
3、在Test Value框中键入原假设的均值数10000。
4、单击Options按钮,得到Options对话框(如图2.3),选项分别是置信度(默认项是95%)和缺失值的处理方式。
选择后默认值后返回主对话框。
图2.3 一个样本t检验的Options对话框5、单击OK,得输出结果。
如表2.1所示。
表2.1(a).数据的基本统计描述One-Sample Statistics表2.1 (b).一个样本均值t检验的检验结果One-Sample Test从上面检验结果表 2.1(a)可以得出国有单位职工工资的平均值、标准差和均值的标准误等反映数据特征的数据。
从表 2.1(b)中可知检验的结果。
即相应的检验统计量t值为4.229,自由度为30,假设检验的P值(sig)小于0.05,故原假设不成立,检验结论是拒绝原假设H0,接受假设H1。
即认为国有企业职工的平均工资与10000元的假设差异显著。
§2.2 两个总体的t 检验§2.2.1 两个独立样本的t检验(Independent-samples T Test)Independent-sample T Test是检验两个没有联系的总体样本均值间是否存在显著的差异,两个没有联系的总体样本也称独立样本。
如两个无联系的企业生产的同样产品之间的某项指标的均值的比较,不同地区的儿童身高、体重的比较等,都可以通过抽取样本检验两个总体的均值是否存在显著的差异。
例2.某医药研究所考察一种药品对男性和女性的治疗效果是否有显著差异,调查了10名男性服用者及7名女性服用者,对他们服药后的各项指标进行综合评分,服用的效果越好,分值就越高,每人所得的总分见表2.2,试根据表中的数据检验这种药品对男性和女性的治疗效果是否存在显著差异。
解:由于药品对男性或女性的影响是无联系的,因此这两个样本是相互独立的。
可以应用两独立样本的假设检验。
首先,建立假设H0:该药品对男性和女性的治疗效果没有显著差异;H1:该药品对男性和女性的治疗效果有显著差异。
表2.2 男,女治疗效果的综合得分表然后,根据表1的数据建立数据文件SY-4,并使用SPSS进行假设检验,具体操作步骤:1、单击Analyze →Compare Means →Independent-sample T Test,打开Independent-sample T Test 主对话框如图2.4。
图2.4 两个独立样本t检验的主对话框2、选择要检验的变量“综合得分”进入检验框中。
3、选择分组变量“性别”进入分组框中,然后单击Define Group按纽,打开分组对话框如2.5图所示,确定分组值后返回主对话框,如果没有分组,可以选择Cut point单选项,并在激活的框内输入一个值作为分组界限值。
4、由Option选择按纽确定置信度值和缺失值的处理方式。
5、点击OK可得输出结果,见表2.3统计分析检验结果。
图2.5 独立样本t检验Define Groups 对话框6、分析输出结果并对结果作出分析见表2.3。
表2.3(a)Group Statistics分组统计描述表表2.3(b)独立样本的均值比较检验表检验表2.3(a) 基本统计表,检验表2.3(b)第三列和第四列是检验两样本数据的方差是否相等,从检验结果得知两样本的方差没有显著差异。
从第五列开始是对两个样本的均值的是否相等进行检验。
从假设检验的P值看出,它大于显著性水平0.05,所以说男女之间的机械能力之间并无显著差异,因此接受原假设H0。
而第八列之后分别是均值差、均值差标准误、均值差的置信区间。
§2.2.2 两个有联系总体间的均值比较(Paired-Sample T Test)Paired-Sample T Test是检验两个有联系正态总体的均值是否存在显著的差异。
又称配对样本的 t 检验。
经常用于生物、医药、农业、工业等多个行业。
如检验某种药品使用的效果是否显著,需要对使用者使用前后进行比较;再如对某种粮食进行品种改良,也需要比较改良前后粮食产量有无显著差异等。
例3:某企业对生产线上的工人进行某种专业技术培训,要对培训效果进行检验,从参加培训的工人中抽取30人,将他们培训前后的数据每加工500个零件的不合格品数进行对比,得到数据表见表2.4。
试根据表中数据检验培训前后工人的平均操作技术水平是否有显著提高,也就是检验培训效果是否显著。
表 2.4 工人培训前后不合格品数据表解:这显然是配对样本均值的假设检验的问题。
所以要建立假设:H0:培训前后工人的技术水平没有显著差异;H1:培训前后工人的技术水平有显著差异;根据表2.3建立数据文件SY-5,根据中心极限定理,在大样本的情况下,样本均值近似地服从正态分布。
所以可以利用正态参数的检验方法进行均值的检验。
其检验过程的具体操作步骤为:1、单击Analyze →Compare Means → Paired-Sample T Test,打开Paired-Sample T Test主对话框如图2.6。
2、选择要检验的两变量进入检验框中,注意,一定要选择两个变量进入检验框内,否则将无法得到检验结果。
3、由Option选择按纽确定置信度值95%和缺失值的处理方式。
4、点击OK得输出结果。
5、根据输出结果作出结论如表2.5所示。
图2.6 配对样本的t检验主对话框表2.5(a) Paired Samples Statistics 样本统计量分析表 2.5(b) Paired Samples Test 配对样本均值差检验表由上表2.5(b)中的检验结果知,假设检验的P值小于0.05,因此可以得出培训前后的差异是显著的,故拒绝假设H0,接受假设H1,认为培训的效果是显著的。
§2.3 单因素方差分析单因变量的单因素方差分析主要解决多于两个总体样本或变量间均值的比较问题。
是一种对多个(大于两个)总体样本的均值是否存在显著差异的检验方法。
其目的也是对不同的总体的数据的均值之间的差异是否显著进行检验。
单因素方差分析的应用范围很广,涉及到工业、农业、商业、医学、社会学等多个方面。
单因素方差分析的应用条件:在不同的水平(因素变量取不同值)下,各总体应当服从方差相等的正态分布。
例4,某企业需要一种零件,现有三个不同的地区的企业生产的同种零件可供选择,为了比较这三个零件的强度是否相同,每个地区的企业抽出6件产品进行强度测试,其值如表2.6所示。
假设每个企业零件的强度值服从正态分布,试检验这三个地区企业的零件强度是否存在显著差异。
解:首先建立假设H 0:三个地区的零件强度无显著差异;H 1:三个地区的零件强度有显著差异。
然后根据表2.6中数据,建立数据文件SY-6并进行单因素方差(One-Way ANOVA )分析。
具体操作过程如下:表2.6 样本零件强度值 单位:百公斤1、单击Analyze → Compare Means → One-Way ANOVA ,打开 One-Way ANOVA 对话框。
图 2.7 单因素方差主对话框2、从左框中选择因变量”零件强度”进入Dependent list 框内,选择因素变量”地区”进入Factor框内。
点击OK就可以得到方差分析表2.7。
表2.7 ANOVA 方差分析表百公斤表2.7是方差分析表,由于F统计量值的P值明显小于显著性水平0.05,故拒绝假设H,认为这三个地区的零件强度有显著差异。
如果需要对各地区间的零件强度进行进一步的比较和分析,可以通过按纽Option选项,contrast对照比较,Post Hoc多重比较去实现。
3、单击Option按纽,打开Option对话框如图2.8所示:在Option选项中选择输出项。
主要有不同水平下样本方差的齐性检验,缺失值的处理方式及均值的图形。
图2.8 单因素方差分析 Options 对话框本例中选择Homogeneity of variance test进行不同水平间方差齐性的检验以及Descriptive 基本统计描述。
在Missing Value栏中选择系统默认项。
完成所有选择后返回主对话框,然后单击OK,就可以得到三个地区零件强度分析表2.8。
表2.8(a) Descriptives基本统计描述表2.8(b)Test of Homogeneity of Variances方差齐性检验百公斤从基本统计分析表2.8(a)可以得到均值、标准差等数据相应的统计特征值。
从表2.8(b)中的统计检验可以得出,因素变量的各水平间的方差是没有显著差异的。
4、Contrasts按纽可以用来进一步分析随着控制变量水平的变化,观测值变化的总体趋势以及进一步比较任意指定水平间的均值差异是否显著。