Sierpinski三角形分形图及其推广
- 格式:pdf
- 大小:240.75 KB
- 文档页数:3

⾃相似性的由来分形理论及其发展历程分形理论及其发展历程被誉为⼤⾃然的⼏何学的分形(Fractal)理论,是现代数学的⼀个新分⽀,但其本质却是⼀种新的世界观和⽅法论。
它与动⼒系统的混沌理论交叉结合,相辅相成。
它承认世界的局部可能在⼀定条件下、过程中、在某⼀⽅⾯(形态,结构,信息,功能,时间,能量等)表现出与整体的相似性,它承认空间维数的变既可以是离散的也可以是连续的,因⽽拓展了视野。
⼀、分形⼏何的概念是美籍法国数学家曼德尔布罗特(B.B.Mandelbrot)1975年⾸先提出的,但最早的⼯作可追朔到1875年,德国数学家维尔斯特拉斯(K.Weierestrass)构造了处处连续但处处不可微的函数,集合论创始⼈康托(G.Cantor,德国数学家)构造了有许多奇异性质的三分康托集。
1890年,意⼤利数学家⽪亚诺(G.Peano)构造了填充空间的曲线。
1904年,瑞典数学家科赫(H.von Koch)设计出类似雪花和岛屿边缘的⼀类曲线。
1915年,波兰数学家谢尔宾斯基(W.Sierpinski)设计了像地毯和海绵⼀样的⼏何图形。
这些都是为解决分析与拓扑学中的问题⽽提出的反例,但它们正是分形⼏何思想的源泉。
1910年,德国数学家豪斯道夫(F.Hausdorff)开始了奇异集合性质与量的研究,提出分数维概念。
1928年布利⼲(G.Bouligand)将闵可夫斯基容度应⽤于⾮整数维,由此能将螺线作很好的分类。
1932年庞特⾥亚⾦(L.S.Pontryagin)等引⼊盒维数。
1934年,贝塞考维奇(A.S.Besicovitch)更深刻地提⽰了豪斯道夫测度的性质和奇异集的分数维,他在豪斯道夫测度及其⼏何的研究领域中做出了主要贡献,从⽽产⽣了豪斯道夫-贝塞考维奇维数概念。
以后,这⼀领域的研究⼯作没有引起更多⼈的注意,先驱们的⼯作只是作为分析与拓扑学教科书中的反例⽽流传开来。
⼆、1960年,曼德尔布罗特在研究棉价变化的长期性态时,发现了价格在⼤⼩尺度间的对称性。

分形数学与艺术结合的明珠大家注意到最近google 图标变成这个样子很多人不明白,这是什么意思,其实这是为了纪念法国数学家Gston Julia是,他发现了在数论中有名的julia序列,就是在这个google LOGO上面看到的数学公式。
通过这个数学公式可以在解析几何上实现很多不规则边的图形。
学名,也叫做分形。
我们在网上搜索了一些资料,为大家做一下分形这个图形学上的概念普及。
认识分形作为一门新兴学科,分形不但受到了科研人员的青睐,而且因为其广泛的应用价值,正受到各行各业人士的关注。
那么,在我们开始学习分形之前,首先应该明白的一件事情是:什么是分形?严格地而且正式地去定义分形是一件非常复杂而且困难的事情。
但是,有一些不太正规的定义却可以帮助我们理解分形的含义。
在这些定义中,最为流行的一个定义是:分形是一种具有自相似特性的现象、图象或者物理过程。
也就是说,在分形中,每一组成部分都在特征上和整体相似,只仅仅是变小了一些而已。
让我们来看下面的一个例子。
下图是一棵厥类植物,仔细观察,你会发现,它的每个枝杈都在外形上和整体相同,仅仅在尺寸上小了一些。
而枝杈的枝杈也和整体相同,只是变得更加小了。
那么,枝杈的枝杈的枝杈呢?自不必赘言。
如果你是个有心人,你一定会发现在自然界中,有许多景物和都在某种程度上存在这种自相似特性,即它们中的一个部分和它的整体或者其它部分都十分形似。
其实,远远不止这些。
从心脏的跳动、变幻莫测的天气到股票的起落等许多现象都具有分形特性。
这正是研究分形的意义所在。
例如,在道·琼斯指数中,某一个阶段的曲线图总和另外一个更长的阶段的曲线图极为相似。
上图中的风景图片又是说明分形的另一很好的例子。
这张美丽的图片是利用分形技术生成的。
在生成自然真实的景物中,分形具有独特的优势,因为分形可以很好地构建自然景物的模型。
除了自相似性以外,分行具有的另一个普遍特征是具有无限的细致性。
上面的动画所演示的是对Mandelbrot集的放大,只要选对位置进行放大,就会发现:无论放大多少倍,图象的复杂性依然丝毫不会减少。

基于领带结Sierpinski分形结构的RFID标签天线作者:刘奕昌关新平来源:《现代电子技术》2008年第05期摘要:基于三角形Sierpinski微带分形贴片,提出了一种新型的小尺寸领带结RFID标签天线设计。
通过仿真,给出了该分形天线的端口特性,同时给出了该领带结型Sierpinski标签天线的谐振频率、方向图以及天线效率。
结果表明,采用不同维数的分形结构,可以实现多频段的工作特性,因而该天线可以很方便地应用于RFID电子标签中。
关键词:Sierpinski分形结构;分形天线;射频识别;电子标签中图分类号:TN82 文献标识码:B文章编号:1004373X(2008)0507402Bow Tie Sierpinski Fractal Structure-based RFID Tag AntennaLIU Yichang,GUAN Xinping(Institute of Electrical Engineering,Yanshan University,Qinhuangdao,066004,China)Abstract:A novel miniaturization bow tie RFID tag antenna is proposed based on the triangular Sierpinski fractal microstrip.The port characteristics of the proposed antenna are presented by simulation.At the same time,the resonance frequency,the radiation pattern and the efficiency of the Sierpinski tag antenna is given.The results of the simulation show that multiple frequency band can be obtained by varying the dimensions of the fractal structure.Hence this kind of antenna can be used into the RFID tag antenna very conveniently.Keywords:Sierpinski fractal structure;fractal antenna;RFID;tag antenna1 引言射频识别(Radio Frequency Identification,RFID)技术是兴起于上世纪90年代的一项自动识别技术[1]。

JavaScript图形实例:SierPinski三角形1.SierPinski三角形Sierpinski三角形是一种分形,由波兰数学家谢尔宾斯基在1915年提出,它是一种典型的自相似集。
其生成过程为:(1)取一个三角形(多数使用等边三角形);(2)沿三边中点连线,将它分成四个小三角形;(3)对上、左、右这三个小三角形重复这一过程。
SierPinski三角形的生成示意如图1所示。
图1 SierPinski三角形的生成SierPinski三角形采用递归过程易于实现,编写如下的HTML代码。
<!DOCTYPE html><head><title>SierPinski三角形</title></head><body><canvas id="myCanvas" width="600" height="600" style="border:3px double #996633;"> </canvas><script type="text/javascript">var canvas = document.getElementById('myCanvas');var ctx = canvas.getContext('2d');var depth =5;ctx.strokeStyle = "red";ctx.lineWidth = 3;function sierpinski(x1,y1,x2,y2,x3,y3,n){if (n<0) return;ctx.beginPath();ctx.moveTo(x1,y1);ctx.lineTo(x2,y2);ctx.lineTo(x3,y3);ctx.lineTo(x1,y1);ctx.closePath();ctx.stroke();var x4 = (x1 + x2) / 2;var y4 = (y1 + y2) / 2;var x5 = (x2 + x3) / 2;var y5 = (y2 + y3) / 2;var x6 = (x1 + x3) / 2;var y6 = (y1 + y3) / 2;sierpinski(x1,y1,x4,y4,x6,y6,n-1);sierpinski(x6,y6,x5,y5,x3,y3,n-1);sierpinski(x4,y4,x2,y2,x5,y5,n-1);}sierpinski(300, 500-500*Math.sqrt(3)/2, 50, 500, 550, 500,depth);</script></body></html>在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出的SierPinski三角形,如图2所示。


分形的图像及应用吕克林【摘要】本文首先阐述了分形的基本概念,并具体介绍了一些典型的分形曲线和分形集,加深读者对分形的理解。
重点描述如何生成分形的计算机图像,以及分形主要的应用领域,强调计算机科学与其他学科之间的紧密联系。
【期刊名称】《创新科技》【年(卷),期】2014(000)024【总页数】3页(P94-96)【关键词】分形;自相似;迭代;Mandelbrot【作者】吕克林【作者单位】河南省科学技术信息研究院,河南郑州 450003【正文语种】中文【中图分类】TP391.4随着计算机图形学的发展,最近几年,分形作为一种艺术形式已经相当流行。
对分形有一个基本的了解,能提高人们的鉴赏力,帮助人们更好地体会分形艺术的美。
分形作为一门刚刚诞生的学科,正在许多领域开展应用和探索。
很多传统的科学难题,都由于分形的引入取得了显著的进展。
1.1 分形的出现。
中国的海岸线有多长?很明显,这取决于测量所用的标度单位。
若以公里为标尺,会遗漏大量的细节,标尺越小,测出的海岸线就越长。
随着计算机的迅速发展,人们在讨论和处理一系列问题的时候,逐渐感到无法描述一些自然界普遍存在的对象,如海岸线,树木,岩石,云团,闪电等等。
同样对于星系分布,凝聚生长,湍流等复杂现象,也需要一门新的学科来描述。
1973年,B.B.Mandelbrot在法兰西学院讲课时,首次提出了分维和分形几何的设想。
Fractal一词由他所创,其原意具有不规则,支离破碎等意义。
分形几何是一门以非规则几何形状为研究对象的学科,也被称为大自然的几何学。
1.2 自相似性。
自相似性是指部分与整体具有相似的性质。
在自然界中,具有自相似性的客观对象是非常多的。
除了山形的起伏,河流的弯曲,树木的分枝结构外,生物体内也有许多例子,如血管或气管的分岔,神经网络等。
抽象的自相似例子就更多了,例如数列0112122312232334…,这是一个去掉奇数项后,仍然得到自身的数列。
下文中将提到的Cantor集是一个更好,更有故事的例子。


由具有D3对称特性的Sierpinski三角形构造球内接二十面体分形图Sierpinski三角形是一种经典的分形图形,它是由一个大三角形和一些递归的小三角形构成的,具有重复自相似的特点。
而球内接二十面体则是一种拥有D3对称性的多面体,它由20个等边三角形和12个正五边形组成,于是产生了一个有意思的想法:是否可以用Sierpinski三角形构建球内接二十面体分形图呢?首先,我们需要了解一下什么是D3对称性。
D3对称性是指一个物体在三维空间中旋转120度或240度或不旋转后仍然能够重合自身。
常常用于描述球内接二十面体这样的多面体。
因此,我们希望构建的分形图也要保持这种D3对称性。
其次,我们需要考虑如何用Sierpinski三角形构建球内接二十面体分形图。
构造分形图的关键在于不断重复、缩小,以产生重复自相似的效果。
具体而言,我们可以从一个正三角形开始,将其划分成四个小三角形,将其中一个去掉,再将其余三个按照原来的形式划分成四个小三角形。
这个过程就是Sierpinski三角形的经典构造流程。
接着,我们考虑如何将这个构造方法用于球内接二十面体。
首先,我们需要将一个大正五边形作为球内接二十面体的参考面。
我们将正五边形的每个顶点与球心相连,将得到12个等长的线段,它们是球内接二十面体的12个棱。
于是,我们可以以这12个线段为基础,构建出一个小的球内接二十面体。
在这个小的球内接二十面体中,正五边形的每条边都相当于一个小的参考面。
接下来,我们将在每个小的参考面上构建Sierpinski三角形。
具体而言,我们以正五边形的每个顶点为中心,向相邻两条棱各作一条垂线,这样我们得到了五个小的正三角形。
然后,我们按照经典的Sierpinski三角形构造方法,在其中四个正三角形上分别再次构建出四个更小的正三角形,最后将其中一个移除。
在这个过程中,我们需要确保所有的小正三角形都贴合在对应的小参考面上。
最后,我们将所有小的球内接二十面体连接在一起,构成一个更大的球内接二十面体分形图。

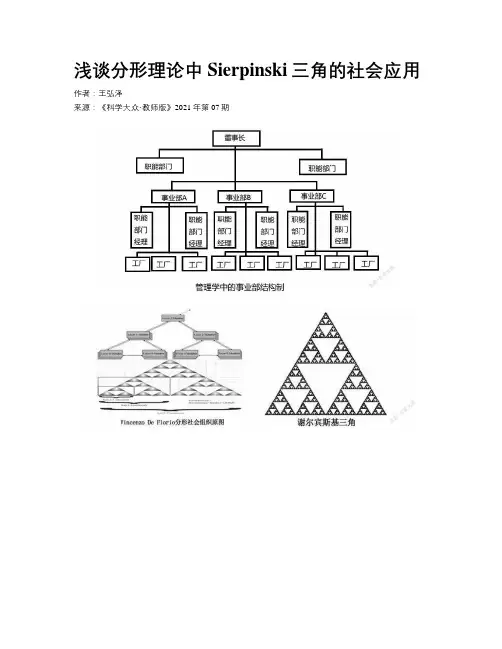
浅谈分形理论中Sierpinski三角的社会应用作者:***来源:《科学大众·教师版》2021年第07期摘要:分形理论与社会治理的结合最早始于欧洲,在我国的发展并不多,但我国目前正处于老龄化进程中,我国在社区与社会治理方面可以吸收欧美学者的理论,进行分形社区建设探索。
通过对比可以发现,不同尺度的自然系统可以给社会分形组织构建提供一定的思路,自相似性与伴生的组织恢复力可以在类似本次疫情的隔离与复工复产、保证社会运转效率方面提供借鉴与参考。
关键词:社会组织; 分形理论; 社会治理; 社区; 谢宾斯基三角中图分类号:O64 文献标识码:A 文章编号:1006-3315(2021)7-196-002一、引言“分形”(fractal)最早是由曼德布罗特在研究英国海岸线的长度问题时提出的概念,其词源来自拉丁语形容词“fractus”,有破碎、生成不规则碎片的意思[1]。
在我国关于分形与社会的研究最早是1990年方曙、黄登仕将分形理论引入社会研究中,提出可以将分形理论用于经济学、情报学、管理科学、思维科学以及文学艺术的研究中。
关于分形组织目前最确切的定义是“分形组织是受生物启发的分层分布式控制体系结构,其组件同时是个体和社会实体。
”(Sousa et al., 2000)。
当前在该领域研究较突出的是安特卫普大学的Vincenzo De Florio教授,在分形社区方面他的研究给予了该领域很多启发。
本文选择“Sierpinski三角”作为分形理论与社会组织的代表进行论述。
二、Sierpinski三角与分形社会组织Vincenzo De Florio認为“分形社会组织是一种旨在最大化社区恢复力的社会技术系统的体系结构,即社区利用现有资源应对、抵御和从不利情况中恢复的持续能力”,事实上特征最显著的分形组织当属军事组织,多数正规军事组织都具有明确的军衔等级和极强的自组织性,训练有素的军人往往在素未谋面的情况下通过军衔就可以实现自组织。

分形——谢尔宾斯基三角形普通几何学研究的对象,一般都具有整数的维数。
比如,零维的点、一维的线、二维的面、三维的立体、乃至四维的时空。
在20世纪70年代末80年代初,产生了新兴的分形几何学(fractal geometry),空间具有不一定是整数的维,而存在一个分数维数。
这是几何学的新突破,引起了数学家和自然科学者的极大关注。
根据物理学家李荫远院士的建议,大陆将fractal一开始就定译为“分形”,而台湾学者一般将fractal译作“碎形”。
——摘自百度百科对于初学Java的同学来说,做分形,的确是一个锻炼思维,熟悉递归算法的好方法,而在众多分形图案中,谢尔宾斯基三角形可以说是比较容易入手的,因为它不管是公式还是图案都比较简单,学会如何用java画歇尔滨斯基三角形后,再画其他图案都会简单很多;今天我们就从歇尔滨斯基三角形入手,进入分形的世界.1、用Java绘制歇尔滨斯基三角形首先要知道如何建立窗体,调取画布对象,如何画线,有一定的数学基础(了解正三角形的性质),还有——数学思维。
2、打开eslips,建立一个Java的工程命名自己命吧,这个随便的哈;(这是我建立的工程)//3、这个程序需要引入的包:import java.awt.Color;import java.awt.Graphics;import javax.swing.JFrame;//4、主类继承JFrame,因此Retangerate拥有所有JFrame的方法public class Retangerate extends JFrame{/*** @param args*/public static void main(String[] args) {// TODO Auto-generated method stubRetangerate a = new Retangerate();a.Draw();}////5、需要创建的方法一:(绘制三角形)//在这个方法里绘出窗体,并生成画布对象public void Draw() {this.setSize(1000,700);this.setLocationRelativeTo(null);this.setDefaultCloseOperation(3);this.setVisible(true);Graphics g = this.getGraphics();//6、定义重绘方法,拖动窗口,改变窗口大小后,绘制的图片仍然留在窗体上}public void paint(Graphics g){super.paint(g);this.Show(100,600,900,600,500,30,200,235,235,10,g);//调用递归函数Show(),所涉及的参数:x1的位置,y1的位置,x2的位置,y2的位置,x3的位置,y3的位置,(以下三个属性是颜色控制,如果需要渐变色彩的话)}public void show(double x,double y,double x2,double y2,doublex3,double y3,int a,int b,int c,int count,Graphics g){int tempx = (int)x;int tempy = (int)y;int tempx2 = (int)x2;int tempy2 = (int)y2;int tempx3 = (int)x3;int tempy3 = (int)y3;if(a<0||b<0||c<0){a=355;b=155;c=35;}//计算出三点的位置g.setColor(new Color(a,b,c));g.drawLine(tempx,tempy,tempx2,tempy2);g.drawLine(tempx,tempy,tempx3,tempy3);g.drawLine(tempx2,tempy2,tempx3,tempy3);if(count>=2){//判断是否进行递归int xm = tempx;int ym = tempy;int xm2 = tempx2;int ym2 = tempy2;int xm3 = tempx3;int ym3 = tempy3;tempx = (xm+xm2)/2;tempy = (ym+ym2)/2;tempx2 = (xm+xm3)/2;tempy2 = (ym+ym3)/2;tempx3 = (xm3+xm2)/2;tempy3 = (ym3+ym2)/2;this.Show(xm,ym,tempx,tempy,tempx2,tempy2,a-10,b-16,c-10,count-1, g);this.Show(tempx,tempy,xm2,ym2,tempx3,tempy3,a-14,b-16,c-18,count-1,g);this.Show(xm3,ym3,tempx2,tempy2,tempx3,tempy3,a-17,b-14,c-0,count -1,g);//由于下次分形要分成三个所以要在一次Show调用自己三次g.drawLine(tempx,tempy,tempx2,tempy2);g.drawLine(tempx,tempy,tempx3,tempy3);g.drawLine(tempx2,tempy2,tempx3,tempy3);}else{return ;}}}。
谢尔宾斯基四边形python谢尔宾斯基四边形(Sierpinski quadrilateral)是一个由波兰数学家谢尔宾斯基(Waclaw Sierpinski)提出的几何图形,它是谢尔宾斯基三角形的二维扩展。
与谢尔宾斯基三角形一样,谢尔宾斯基四边形也具有自相似性和分形特征。
在本文中,我们将探讨谢尔宾斯基四边形的构造方法和一些有趣的性质。
谢尔宾斯基四边形的构造方法非常简单。
首先,我们从一个正方形开始,将其分成四个相等的小正方形。
然后,我们在每个小正方形的中心位置画一个小正方形,再将原始正方形删去。
接下来,我们重复这个过程,不断地在每个新生成的小正方形中继续构造更小的正方形。
经过无限次的迭代,我们将得到一个具有分形结构的谢尔宾斯基四边形。
谢尔宾斯基四边形具有许多有趣的性质。
首先,它是一个无限细分的几何图形,即使在无限次迭代后,我们仍然可以找到更小的四边形。
其次,谢尔宾斯基四边形是自相似的,即每个较大的四边形都由四个较小的四边形组成,这种自相似性质使得谢尔宾斯基四边形展现出美妙的几何美感。
谢尔宾斯基四边形还具有一些有趣的数学特性。
首先,它的维度是介于一维和二维之间的,即分形维度。
其次,谢尔宾斯基四边形的面积为零,但是它的边界长度却是无穷大的。
这种有趣的数学特性使得谢尔宾斯基四边形成为了研究分形几何学的重要对象。
除了数学上的研究,谢尔宾斯基四边形还有一些实际应用。
例如,在计算机图形学中,谢尔宾斯基四边形可以用来生成逼真的纹理和景深效果。
此外,谢尔宾斯基四边形还可以用来设计迷宫游戏和艺术品,给人们带来视觉上的享受和思考的乐趣。
谢尔宾斯基四边形是一个具有迷人美学和丰富数学特性的几何图形。
它的构造简单而有趣,展现了分形几何学的魅力。
通过研究谢尔宾斯基四边形,我们可以更好地理解分形结构和自相似性,同时也能够应用它在计算机图形学和艺术创作中。
谢尔宾斯基四边形的研究不仅展示了数学的美妙之处,也为我们带来了无限的思考和探索的空间。
非线性动力学学习报告在课堂上老师以生动活泼的方式介绍了分形的相关知识,特别是展现了一些美丽的分形图案,我对此十分感兴趣,所以课后找了一些相关资料,学会了用仿射变换的循环迭代方法,在MATLAB 平台下,实现了一些简单的飞行图案的绘制。
具体内容见项目一。
其中的数学原理由于我还不是特别清楚,所以在此进仅做一简要汇报,下面会具体叙述用MATLAB 绘制分形图案的过程。
在项目二中,探讨了对于一根细长压杆,端部的压力大小与杆件变形之间的关系。
这里的端部压力是较大的载荷(即大于临界力),那么经典的材料力学理论便束手无策,这里构建了一个压杆变形的微段迭代模型,把一个大变形非线性问题转化为有限个小变形的迭加,用MATLAB 编程迭代计算的结果较好的吻合了铁木辛哥弹性稳定理论中有关压杆弹性屈曲中的一些成果。
项目一:用MATLAB 绘制美丽的分形图案上个世纪60年代,B.Mandelbrot 对一个具有复杂几何性质但局部看起来仍然一样的几何对象提出了分形概念。
在很多非线性动力学系统等血多领域都会看到分形的例子,随着电子计算机的发展,我们绘制出了很多分形图案。
在这个项目中,实现了用MATLAB 来绘制蕨类植物枝叶和著名的Sierpinski 三角形;另外还给出了一个通过编程绘制树枝的例子没有用到仿射变换,只是复杂的循环。
经过翻阅相关资料(考文献[1]),我了解到数学中的仿射变换的定义如下:设x 是一个n 维向量,A 是n*n 的矩阵,b 是与x 同维的向量,那么变换b Ax x +→称作仿射变换,去不同的A ,b 就会得到不同的变换结果。
如果打印前k 次(k 应该取较大的值)迭代过程中向量x 在坐标系中所表示的所有点,那么就可以得到一幅漂亮的分形图案。
其中矩阵A 和向量b 的取法涉及到很复杂的数学理论,在这里不做详细介绍。
基于前面的理论分析很容易得到MATLAB 绘图程序代码及其运行结果。
1.、使用数学中的仿射变换理论,绘制蕨类植物枝叶程序:%fenxing_juelei.m%蕨类植物模拟x = [.5; .5]; %初值h = plot(x(1),x(2),'.'); %绘制初值点%设置用于后面随机数的判别向量p = [ .85 .92 .99 1.00];b1 = [0; 1.6];b2 = [0; 1.6];b3 = [0; .44];%------仿射变换矩阵A1 = [ .85 .04; -.04 .85];A2 = [ .20 -.26; .23 .22];A3 = [-.15 .28; .26 .24];A4 = [ 0 0 ; 0 .16];for i=1:20000r = rand; %产生随机数if r < p(1)x = A1*x + b1;elseif r < p(2)x = A2*x + b2;elseif r < p(3)x = A3*x + b3;elsex = A4*x;endplot(x(1),x(2),'g'),hold on %采用绿色绘制endaxis off %取消坐标轴把该m文件放置到Matlab的当前工作目录下在命令行中输入fenxing_juelei,变得到了下面的运行结果。
分形图形学实验报告指导实验报告要求1. 实验名称2. 实验目的、要求3. 实验主要内容(某某算法的实现)4. 实验过程(程序流程图、源代码)5. 实验结果(附上打印的图形)6. 实验小结实验报告一一般分形图形生成实验目的1. koch曲线、sierpinski三角形、cantor集的计算机实现2. 掌握用迭代、递归生成分形实验内容及步骤1、 koch曲线函数:plot(x1,y1) –(x2,y2) (画直线函数)sin( ) (正弦函数)cos( ) (余弦函数)arctan( ) (反正切函数)12、 sierpinski三角形函数: plot(x1,y1) –(x2,y2) (画直线函数)sin( ) (正弦函数)cos( ) (余弦函数)23、 cantor集3实验报告二 l系统语言生成分形图形实验目的1. 掌握用l系统语言生成分形2. koch曲线、sierpinski三角形、cantor集的l系统实现4实验内容及步骤1. 编写程序用l系统语言生成分形图形1) 编写程序生成koch曲线:初始图形是一条线段,生成过程是将线段中间1/3向外折起。
程序伪码如下:kochcurve { ;柯赫曲线angle 6 ;角度增量是60°axiom f ;初始图形是一单位线段f=f+f--f+f ;产生式是将线段中间1/3折起} ;结束2) 用l系统再次生成sierpinski三角。
生成sierpinski三角的伪码如下:hilbert{ ;sierpinski三角,1996-12 angle 4 axiom y ;初始串为任意字母y x=-yf+xfx+fy- ;第一个生成规则y=+xf-yfy-fx+ ;第二个生成规则,由以上规则不断代换 } 3) 模拟草本植物。
注意这里出现了“括号”——可以方便地表示树枝,伪码如下:herbplant { ;生成植物,本程序使用了括号angle 14axiom zz=zfx[+z][-z]x=x[-fff][+fff]fx}5篇二:光学实验报告建筑物理——光学实验报告实验一:材料的光反射比、透射比测量实验二:采光系数测量实验三:室内照明实测实验小组成员:指导老师:日期:2013年12月3日星期二实验一、材料的光反射比和光透射比测量一、实验目的与要求室内表面的反射性能和采光口中窗玻璃的透光性能都会直接或间接的影响室内光环境的好坏,因此,在试验现场采光实测时,有必要对室内各表面材料的光反射比,采光口中透光材料的过透射比进行实测。
不可思议的分形图形讲数学之美,分形图形是不可不讲的。
如果说有什么东西能够让数学和艺术直接联系在一起,答案毫无疑问就是分形图形。
让我们先来看一个简单的例子。
首先画一个线段,然后把它平分成三段,去掉中间那一段并用两条等长的线段代替。
这样,原来的一条线段就变成了四条小的线段。
用相同的方法把每一条小的线段的中间三分之一替换成一座小山,得到了16条更小的线段。
然后继续对这16条线段进行类似的操作,并无限地迭代下去。
图1是这个图形前五次迭代的过程,可以看到第五次迭代后图形已经相当复杂,我们已经无法看清它的全部细节了。
图 1你可能注意到一个有趣的事实:整个线条的长度每一次都变成了原来的如果最初的线段长度为一个单位,那么第一次操作后总长度变成了第二次操作后总长度增加到第n次操作后总长度为毫无疑问,操作无限进行下去,这条曲线将达到无限长。
难以置信的是这条无限长的曲线却“始终只有那么大”。
现在,我们像图2那样,把3条这样的曲线首尾相接组成一个封闭图形。
这时,有趣的事情发生了,这个雪花状的图形有着无限长的边界,但是它的总面积却是有限的。
有人可能会说,为什么面积是有限的呢?虽然从图2看结论很显然,但这里我们还是要给出一个简单的证明。
3条曲线中每一条在第n次迭代前都有4n-1条长为的线段,迭代后多出的面积为4n-1个边长为的等边三角形。
把4n-1扩大到4n,再把所有边长为的等边三角形扩大为同样边长的正方形,总面积仍是有限的,因为无穷级数是收敛的。
很难相信,这一块有限的面积,竟然是用无限长的曲线围成的。
图 2这让我们开始质疑“周长”的概念了:剪下一个直径为1厘米的圆形纸片,它的周长真的就是π厘米吗?拿放大镜看看,我们就会发现纸片边缘并不是平整的,上面充满了小锯齿。
再用显微镜观察,说不定每个小锯齿上也长有很多小锯齿。
然后,锯齿上有锯齿,锯齿上又有锯齿,周长永远也测不完。
分形领域中有一个经典的说法,“英国的海岸线有无限长”,其实就是这个意思。
谢尔宾斯基三角形(Sierpinski triangle )是一种分形,由波兰数学家谢尔宾斯基在1915年提出。
它是自相似集的例子(自相似是近乎或确实和它的一部分相似).
分形,是几何学术语,通常被定义为“一个粗糙或零碎的几何形状,可以分成数个部分,且每一部分都(至少近似地)是整体缩小后的形状”。
构造过程如下:取一个实心的三角形(多数使用等边三角形),挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形),然后在剩下的小三角形中又挖去一个“中心三角形”,不断重复以上过程,那么剩下的三角形我们称为谢尔宾斯基三角形.
小试牛刀
1.如图,有一个大三角形,面积为1,联结三角形各边的中点得到一个小三角形,再联结这个小三角形各边的中点又得到一个更小的三角形,如此无限继续下去.问黄色阴影部分的面积是多少?_________.
(A)45 (B) 58 (C) 78
(D) 35。