局部受压例题
- 格式:doc
- 大小:50.00 KB
- 文档页数:2

关于砌体局部受压承载力问题的讨论下图所示某梁截面尺寸为250mm ×550mm ,支承在具有壁柱的砖墙上,支承长度a =370mm ,N l =60kN ,σ0=0.48N/mm 2,采用MU10砖及M2.5混合砂浆。
(1)求梁端受压局部承载力。
(2)若N l =85kN ,设置刚性垫块a b ×b b ×t b =370 mm ×490mm ×180 mm ,试验算垫块下砌体局部受压承载力。
习题图解:(1) 由MU10、M2.5知: f =1.3MPaa 0=10 2063.1/55010/=⨯=f h c mmA l = a 0·b=206·250=51500mm 2A 0=490×(250+2×240)-250×(250+2×240-490) =297700mm 2或保守计算为:A 0=490×490=240100mm 2γ =1+0.35 ×67.11/0=-l A A A 0/A l =4.7>3 , ψ=0ηγA l f =0.7×1.67×51500×1.3×10-3=78.3kN>N l =60kN安全。
(2)N l =85kN 刚性垫块a b ×b b ×t b =370 mm ×490mm ×250 mmA b =370×490=181300mm 2 N 0=σ0 A b =87.02kNσ0 /f =0.48/1.30=0.369 由表4-5得:δ1 =5.95a 0= 38.1223.1/55095.5/1=⨯=f h δmme = mm 2.6702.8785)38.1224.02/370(85=+⨯-⨯ b a e = 3702.67 =0.18,β≤3 查表得:ϕ=0.716 A 0=4902=240100mm 22.1135.010=-+=bA A γ γ1=0.8γ=0.96<1 取γ1=1.0f A b 1ϕγ=0.716×181300×1.3=168.754k N ≈N l + N 0=172.02kN 相差不超过5%,基本安全。
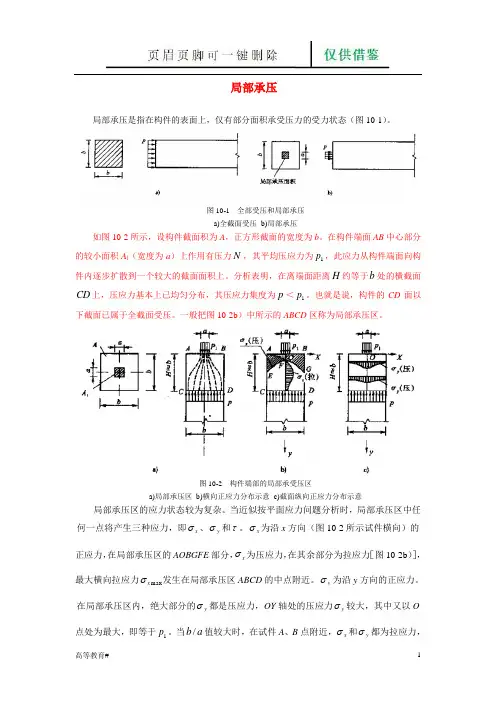
局部承压局部承压是指在构件的表面上,仅有部分面积承受压力的受力状态(图10-1)。
图10-1 全部受压和局部承压a)全截面受压 b)局部承压如图10-2所示,设构件截面积为A ,正方形截面的宽度为b 。
在构件端面AB 中心部分的较小面积A l (宽度为a )上作用有压力N ,其平均压应力为1p ,此应力从构件端面向构件内逐步扩散到一个较大的截面面积上。
分析表明,在离端面距离H 约等于b 处的横截面CD 上,压应力基本上已均匀分布,其压应力集度为p <1p 。
也就是说,构件的CD 面以下截面已属于全截面受压。
一般把图10-2b )中所示的ABCD 区称为局部承压区。
图10-2 构件端部的局部承受压区a)局部承压区 b)横向正应力分布示意 c)截面纵向正应力分布示意局部承压区的应力状态较为复杂。
当近似按平面应力问题分析时,局部承压区中任何一点将产生三种应力,即x σ、y σ和τ。
x σ为沿x 方向(图10-2所示试件横向)的正应力,在局部承压区的AOBGFE 部分,x σ为压应力,在其余部分为拉应力[图10-2b )],最大横向拉应力m ax x σ发生在局部承压区ABCD 的中点附近。
y σ为沿y 方向的正应力。
在局部承压区内,绝大部分的y σ都是压应力,OY 轴处的压应力y σ较大,其中又以O 点处为最大,即等于1p 。
当/b a 值较大时,在试件A 、B 点附近,x σ和y σ都为拉应力,但其值都不大。
局部受压区内混凝土的抗压强度情况,可用图10-3所示承压面积相同(150mm ×150mm ),而试件外形尺寸不同的混凝土轴心受压试验的抗压强度对比来说明,其中局部承压试件尺寸为450mm ×450mm ×450mm ,局部承压面积(以钢垫板计)为150mm ×150mm 。
试验结果表明,局部承压试件的抗压强度远高于同样承压面积的棱柱体抗压强度(全截面受压),这主要是垫板下直接受压的混凝土的横向变形,不仅受钢垫板与试件表面之间摩擦力的约束,而且更主要的是受试件外围混凝土的约束,中间部分混凝土纵向受压引起的横向扩张,使外围混凝土受拉,其反作用力又使中间混凝土侧向受压,限制了纵向裂缝的开展,因而其强度比棱柱体抗压强度大很多。

{例题2-10}某带壁柱墙,截面尺寸如图2-26所示,采用烧结普通砖MU10、水泥混合砂浆M5砌筑,施工质量控制等级为B级。
墙上支撑截面尺寸为200mm X 500mm的钢筋混凝土梁,梁端搁置长度为370mm,梁端支承压力设计值为75KN,上部轴向力设计值为170KN。
试验算梁端支承处砌体的局部受压承载力。
解题思路:该墙为T形截面,应注意T型截面时影响砌体局部抗压强度的计算面积A0的确定方法。
未设置垫块时,A0中英包括医院部分的面积;设置刚性垫块后,A0只取壁柱范围内的面积,而不应计入翼缘部分的面积。
{解}本题属图2-18(b)情况的局部受压由表2-3,f=1.50MPaA0=0.37X0.37+2X0.155XO.24=0.2113㎡(见图2-26a)按式(2-54),并取=0.7,得=0.7x1.77x1.50x0.036x1000=66.9KN<75KN。
故梁端支承处砌体的局部受压不安全。
现设置370mmX370mmX180mm的预制混凝土块(见图2-26b),其尺寸符合刚性垫块的要求且垫块伸入翼缘内的长度符合要求。
的作用点由刚性垫块时梁端有效支承长度确定,= =0.33,由表2-12,=5.9,按式(2-62)=0.7x1.0x1.50x0.1369x1000=143.7KN>143.4kn.梁端支撑处砌体局部受压安全。
{例题2-11}某窗间墙截面尺寸为1000mm X 190mm,采用混凝土小型空心砌块MU7.5、水泥混合砂浆Mb5砌筑,施工质量控制等级为B级。
墙上支撑截面尺寸为200mm X 400mm 的钢筋混凝土梁,梁端支承压力设计值为50KN,上部轴向力设计值为90KN。
式验算梁端支撑处砌体的局部受压承载力{解}本题属于2-18(a)情况的局部受压。
由表2-5,f=1.71MPaA0=(b+2h)h=(0.2+2x019)x0.19=0.1102㎡由式(2-53), = = =153mm= =0.153x0.2=0.0306㎡对于未灌孔混凝土砌块砌体,取γ=1.0按式(2-54)并取=0.7,得=0.7x1.0x1.71x0.0306x1000=36.6KN<50KN。

砌体结构局部受压计算问题分析高 智江苏沪宁钢机股份有限公司,北京 100125摘 要:由于《砌体结构设计规范》(GB 50003—2011)在砌体局部受压承载力计算方法上存在一些不足,因此文章通过具体结构例题的计算,给出《砌体结构设计规范》(GB 50003—2011)中各个公式计算参数的合理取值,并建议在梁端增设梁垫,以此来提高砌体结构局压能力。
关键词:砌体结构;局部受压;梁垫中图分类号:TU364文献标志码:A文章编号:2096-2789(2021)02-0034-021 概述砌体结构因其技术成熟、应用广泛、工程造价较为低廉,目前仍然在一些多层建筑中应用。
局部受压(以下简称“局压”)是砌体结构中的主要受力状态之一,由于局压造成的破坏在工程实际中并不少见,且后果严重,修复困难,甚至曾出现过因砌体局部抗压强度不足而发生房屋倒塌的事故,因此正确计算砌体局压承载力很有必要。
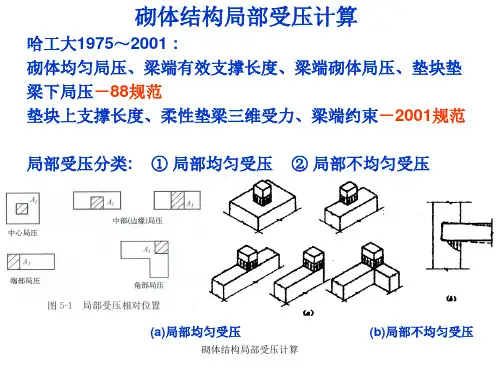
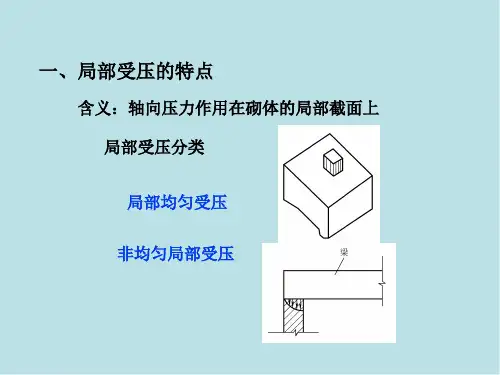
局压计算按其相对位置不同又可分为下列几种受荷情况:中心局压、中部或边缘局压、端部局压和角部局压。
试验表明,局压相对位置是影响局压承载力很重要的因素之一[1]。
文章选取2个算例来说明,算例平面布置如图1所示(见图1中节点1和节点2)。
(2)梁下砌体的局压面积上受到的是均匀压力。
《规范》第5.2.1条指出,砌体截面中受局部均匀压力时的承载力应满足下式的要求:(1)式中:N l 为局压面积上的轴向力设计值,由于为中间节点,因此应为左右两侧次梁梁端剪力之和,此处与节点2类型的梁端情况不同,节点2只考虑单侧梁端的剪力。
γ为砌体局部抗压强度提高系数,实际是考虑局部压力存在力的扩散以及周围砌体对局压范围内的砌体施加约束作用,使强度得以提高。
《规范》在计算γ时给出4种情况,如图2所示。
其中,(a)为四面约束;(b )为三面约束;(c)为两面约束;(d )为单面约束。
可见约束得越多,强度提高得越多,而此例中实际情况虽然和图2(b )情况很像,但应按图2(c)情况计算,即都属于两面约束,γ≤1.5。





局部受压例题1、砌体局部均匀受压【解】局部受压面积 A l =250×250=62500mm 2A 0=(a+2h)h==(250+2×370)×370=366300mm 2砌体局部抗压强度提高系数查表得MU10烧结普通砖和M5水泥砂浆砌筑的砌体的抗压强度设计值为 f =1.5MPa ,采用水泥砂浆应乘以调整系数γa =0.9; 砌体局部受压承载力γfA =1.77×0.9×1.5×62500=149344 N =149.3kN >120kN砌体局部受压承载力满足要求。
【例1】一钢筋混凝土柱截面尺寸为250mm ×250mm ,支承在厚为370mm 的砖墙上,作用位置如图所示,砖墙用MU10烧结普通砖和M5水泥砂浆砌筑,柱传到墙上的荷载设计值为120KN 。
试验算柱下砌体的局部受压承载力。
135.01-+=lo A Aγ1 1.772=+=<2、梁端支承处砌体的局部受压(不考虑上部荷载)【解】由表查得砌体抗压强度设计值f=1.5N/mm 2。
有效支承长度 a 0=163.3mm局部受压面积 Al=a 0b=32660mm 2 局部受压计算面积A 0=h(2h+b)= 347800mm 2A 0/A l =10.7>3故上部荷载折减系数ψ=0,可不考虑上部荷载的影响 梁底压力图形完整系数η=0.7。
局部抗压强度提高系数γ=2.09>2.0取γ=2.0。
局部受压承载力验算ηγfA l =68.586kN <ψN 0+N l =80kN 不满足要求 【例2】试验算房屋处纵墙上梁端支承处砌体局部受压承载力。
已知梁截面为200mm ×400mm ,支承长度为240mm ,梁端承受的支承压力设计值Nl=80kN ,上部荷载产生的轴向力设计值Nu=260kN ,窗间墙截面为1200mm ×370mm 采用MU10烧结普通砖及M5混合砂浆砌筑。
局部受压例题
1、砌体局部均匀受压
【解】局部受压面积 A l =250×250=62500mm 2
A 0=(a+2h)h==(250+2×370)×370=366300mm 2
砌体局部抗压强度提高系数
查表得MU10烧结普通砖和M5水泥砂浆砌筑的砌体的抗压强度设计值为 f =1.5MPa ,采用水泥砂浆应乘以调整系数γa =0.9; 砌体局部受压承载力γfA =1.77×0.9×1.5×62500
=149344 N =149.3kN >120kN
砌体局部受压承载力满足要求。
【例1】一钢筋混凝土柱截面尺寸为250mm ×250mm ,支承在厚为370mm 的砖墙上,作用位置如图所示,砖墙用MU10烧结普通砖和M5水泥砂浆砌筑,柱传到墙上的荷载设计值为120KN 。
试验算柱下砌体的局部受压承载力。
135.01-+=l
o A A
γ1 1.772=+=<
2、梁端支承处砌体的局部受压(不考虑上部荷载)
【解】由表查得砌体抗压强度设计值f=1.5N/mm 2。
有效支承长度 a 0=163.3mm
局部受压面积 Al=a 0b=32660mm 2 局部受压计算面积
A 0=h(2h+b)= 347800mm 2
A 0/A l =10.7>3
故上部荷载折减系数ψ=0,可不考虑上部荷载的影响 梁底压力图形完整系数η=0.7。
局部抗压强度提高系数
γ=2.09>2.0
取γ=2.0。
局部受压承载力验算
ηγfA l =68.586kN <ψN 0+N l =80kN 不满足要求 【例2】试验算房屋处纵墙上梁端
支承处砌体局部受压承载力。
已
知梁截面为200mm ×400mm ,支
承长度为240mm ,梁端承受的支
承压力设计值Nl=80kN ,上部荷
载产生的轴向力设计值
Nu=260kN ,窗间墙截面为
1200mm ×370mm 采用MU10
烧结普通砖及M5混合砂浆砌筑。