第十章 隐马尔科夫模型
- 格式:pdf
- 大小:1.96 MB
- 文档页数:50

隐马尔可夫模型算法
隐马尔可夫模型算法是一种用于序列数据分析的统计模型,它可以用来预测未来的状态或者根据已知的状态推断出隐藏的状态。
这种模型在自然语言处理、语音识别、生物信息学等领域都有广泛的应用。
隐马尔可夫模型算法的基本思想是,将一个系统看作是由一系列状态组成的,每个状态都有一个对应的观测值。
这些状态之间的转移是随机的,而观测值则是由状态生成的。
因此,我们可以通过观测值来推断出隐藏的状态,或者根据已知的状态来预测未来的观测值。
在隐马尔可夫模型算法中,我们需要定义两个概率分布:状态转移概率和观测概率。
状态转移概率指的是从一个状态转移到另一个状态的概率,而观测概率则是在某个状态下观测到某个观测值的概率。
这些概率可以通过训练数据来估计,通常使用最大似然估计或者贝叶斯估计。
隐马尔可夫模型算法的核心是前向-后向算法和维特比算法。
前向-后向算法用于计算给定观测序列下,某个状态出现的概率。
维特比算法则用于寻找最可能的状态序列,即给定观测序列下,最可能的状态序列。
隐马尔可夫模型算法的应用非常广泛。
在自然语言处理中,它可以用于词性标注、命名实体识别、机器翻译等任务。
在语音识别中,
它可以用于声学模型的建立。
在生物信息学中,它可以用于DNA序列分析、蛋白质结构预测等任务。
隐马尔可夫模型算法是一种非常强大的序列数据分析工具,它可以用于各种领域的任务。
虽然它的理论比较复杂,但是在实际应用中,我们可以使用现有的库或者工具来实现它,从而更加方便地应用它。

隐马尔可夫模型参数估计
隐马尔可夫模型参数估计是指在隐马尔可夫模型中,根据观
测数据估计模型参数的过程。
隐马尔可夫模型是一种概率模型,
它用来描述一个隐藏状态序列的概率分布,它可以用来描述一个
隐藏状态序列的概率分布,以及它们之间的转移概率。
隐马尔可
夫模型参数估计是一个复杂的过程,它需要根据观测数据来估计
模型参数,以便更好地描述隐藏状态序列的概率分布。
隐马尔可夫模型参数估计的方法有很多,其中最常用的是最
大似然估计法。
最大似然估计法是一种概率模型参数估计的方法,它的基本思想是,根据观测数据,求出使得观测数据出现的概率
最大的模型参数。
另外,还有一些其他的参数估计方法,比如最
小二乘法、最小化KL散度等。
隐马尔可夫模型参数估计的结果可以用来描述隐藏状态序列
的概率分布,以及它们之间的转移概率。
此外,它还可以用来预
测未来的状态,以及推断未知的状态。
因此,隐马尔可夫模型参
数估计是一个非常重要的过程,它可以帮助我们更好地理解隐藏
状态序列的概率分布,以及它们之间的转移概率。

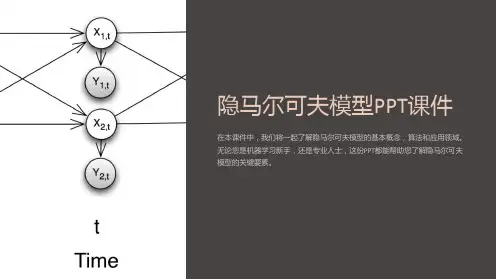
隐马尔可夫模型维特比算法尝试(一)隐马尔可夫模型基本概念隐马尔可夫模型是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测而产生观测随机序列的过程。
隐藏的马尔可夫链随机生成的状态序列,称为状态序列(state sequence );每个状态生成一个观测,而由此产生的观测的随机序列,称为观测序列(observation sequence )。
序列的每个位置又可以看作是一个时刻。
隐马尔可夫模型由初始概率分布、状态转移概率分布以及观测概率分布确定。
隐马尔可夫模型的形式定义如下:设Q 是所有可能的状态的集合,V 是所有可能的观测的集合。
12{,,,}N Q q q q = 12{,,,}M V v v v =I 是长度为T 的状态序列,O 是对应的观测序列。
12{,,,}T I i i i = 12{,,,}T O o o o =A 是状态转移概率矩阵:[]N N A ij a ⨯=其中,1()ij t j t i a P i q i q +===1,2,,i N = ;1,2,,j N =是在时刻t 处于状态i q 的条件下在时刻1t +转移到状态j q 的概率。
B 是观测概率矩阵:[()]N M B j b k ⨯=其中,()()j t k t j b k P o v i q ===1,2,,k M = ;1,2,,j N =是在时刻t 处于状态j q 的条件下生成观测k v 的概率。
π是初始状态概率向量:()i ππ=其中,1()i i P i q π==1,2,,i N =是时刻1t =处于状态i q 的概率。
隐马尔可夫模型的3个基本问题:(1) 概率计算问题。
给定模型和观测序列,计算在模型下观测序列出现的概率。
(2) 学习问题。
已知观测序列,估计模型参数,使得在该模型下观测序列概率最大。
即用极大似然估计的方法估计参数。
(3) 预测问题,也称为解码(decoding )问题。



机器学习_隐马尔可夫模型HMM1. 马尔可夫链马尔可夫链是满足马尔可夫性质的随机过程。
马尔可夫性质是无记忆性。
也就是说,这一时刻的状态,受且只受前一时刻的影响,而不受更往前时刻的状态的影响。
我们下面说的隐藏状态序列就马尔可夫链。
2. 隐马尔可夫模型隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,用它处理的问题一般有两个特征:第一:问题是基于序列的,比如时间序列,或者状态序列。
第二:问题中有两类数据,一类序列数据是可以观测到的,即观测序列;而另一类数据是不能观测到的,即隐藏状态序列,简称状态序列,该序列是马尔可夫链,由于该链不能直观观测,所以叫“隐”马尔可夫模型。
简单地说,状态序列前项能算出后项,但观测不到,观测序列前项算不出后项,但能观测到,观测序列可由状态序列算出。
HMM模型的主要参数是λ=(A,B,Π),数据的流程是通过初始状态Pi生成第一个隐藏状态h1,h1结合生成矩阵B生成观测状态o1,h1根据转移矩阵A生成h2,h2和B再生成o2,以此类推,生成一系列的观测值。
HMM3. 举例1) 问题描述假设我关注了一支股票,它背后有主力高度控盘,我只能看到股票涨/跌(预测值:2种取值),看不到主力的操作:卖/不动/买(隐藏值:3种取值)。
涨跌受主力操作影响大,现在我知道一周之内股票的涨跌,想推测这段时间主力的操作。
假设我知道有以下信息:i. 观测序列O={o1,o2,...oT} 一周的涨跌O={1, 0, 1, 1, 1}ii. HMM模型λ=(A,B,Π)•隐藏状态转移矩阵A 主力从前一个操作到后一操作的转换概率A={{0.5, 0.3,0.2},{0.2, 0.5, 0.3},{0.3, 0.2, 0.5}}•隐藏状态对观测状态的生成矩阵B(3种->2种)主力操作对价格的影响B={{0.6, 0.3, 0.1},{0.2, 0.3, 0.5}}•隐藏状态的初始概率分布Pi(Π)主力一开始的操作的可能性Pi={0.7, 0.2,0.1}2) 代码c) 分析这里我们使用了Python的马尔可夫库hmmlearn,可通过命令 $ pip install hmmlearn安装(sklearn的hmm已停止更新,无法正常使用,所以用了hmmlearn库)马尔可夫模型λ=(A,B,Π),A,B,Π是模型的参数,此例中我们直接给出,并填充到模型中,通过观测值和模型的参数,求取隐藏状态。




隐马尔可夫模型的原理与实现隐马尔可夫模型(Hidden Markov Model,HMM)是一种统计模型,广泛应用于序列数据分析、模式识别、自然语言处理等领域。
其基本原理是假设观测序列是通过一个不可见的状态序列产生的,通过观测序列预测状态序列或反向估计状态序列。
HMM包含三个基本组成部分:状态集合、观测集合和状态转移概率矩阵。
状态集合表示系统可能的状态,观测集合表示观测到的数据,状态转移概率矩阵表示从一个状态转移到另一个状态的概率。
在HMM中,将一个观测序列用O表示,状态序列用Q表示,通过条件概率来描述观测序列和状态序列之间的关系。
观测序列O和状态序列Q的联合概率可以用如下公式表示:P(O,Q) = P(O|Q)P(Q)其中,P(O|Q)表示给定状态序列Q时观测序列O的概率,P(Q)表示状态序列Q的概率。
HMM的实现主要包括三个问题:观测序列概率计算问题、状态序列解码问题和模型参数学习问题。
1. 观测序列概率计算问题:给定一个HMM模型和观测序列O,计算观测序列O在该模型下的概率P(O)。
该问题可以通过前向算法和后向算法解决。
前向算法通过递推的方式计算从状态i观测到O中的第t个观测的概率,在t时刻在状态i的概率P(i, t)可以通过如下公式计算:P(i, t) = P(O_1, O_2, ..., O_t, q_t=i)其中O_1, O_2, ..., O_t表示观测序列中的前t个观测。
后向算法通过递推的方式计算从状态i观测到O中的第t+1个观测到最后一个观测的概率,在t时刻在状态i的概率P(i, t)可以通过如下公式计算:P(i, t) = P(O_t+1, O_t+2, ..., O_T|q_t=i)其中O_t+1, O_t+2, ..., O_T表示观测序列中的后t个观测。
观测序列概率计算问题的解决方法是前向-后向算法,通过前向算法计算前向概率α和后向算法计算后向概率β,然后计算任意时刻t时在状态i的概率P(i, t),最终观测序列概率P(O)等于最后时刻在所有状态的概率之和。
机器学习中的隐马尔可夫模型解析隐马尔可夫模型(Hidden Markov Model,HMM)是一种常用于描述随机过程的概率模型,在机器学习领域得到广泛应用。
本文将对隐马尔可夫模型的原理、应用以及解析方法进行详细介绍。
一、隐马尔可夫模型的基本原理隐马尔可夫模型由两个基本假设构成:马尔可夫假设和观测独立假设。
根据这两个假设,隐马尔可夫模型可以表示为一个五元组:(N, M, A, B, π),其中:- N表示隐藏状态的数量;- M表示观测状态的数量;- A是一个N×N的矩阵,表示从一个隐藏状态转移到另一个隐藏状态的概率;- B是一个N×M的矩阵,表示从一个隐藏状态生成一个观测状态的概率;- π是一个长度为N的向量,表示初始隐藏状态的概率分布。
在隐马尔可夫模型中,隐藏状态无法被直接观测到,只能通过观测状态的序列来进行推断。
因此,对于给定的观测状态序列,我们的目标是找到最有可能生成该序列的隐藏状态序列。
二、隐马尔可夫模型的应用领域隐马尔可夫模型在自然语言处理、语音识别、图像处理等领域得到广泛应用。
以下是几个常见的应用场景:1. 自然语言处理:隐马尔可夫模型可以用于词性标注、语法分析等任务,通过学习文本中的隐藏状态序列来提取语义信息。
2. 语音识别:隐马尔可夫模型可以用于音频信号的建模,通过观测状态序列推断出音频中的语音内容。
3. 图像处理:隐马尔可夫模型可以用于图像分割、目标跟踪等任务,通过学习隐藏状态序列来提取图像中的特征。
三、隐马尔可夫模型的解析方法解析隐马尔可夫模型有两个基本问题:评估问题和解码问题。
1. 评估问题:给定模型参数和观测状态序列,计算生成该观测序列的概率。
一种常用的解法是前向算法,通过动态规划的方式计算前向概率,即在第t个时刻观测到部分序列的概率。
2. 解码问题:给定模型参数,找到最有可能生成观测状态序列的隐藏状态序列。
一种常用的解法是维特比算法,通过动态规划的方式计算最大后验概率路径,即在第t个时刻生成部分观测序列的概率最大的隐藏状态路径。
隐马尔可夫模型三个基本问题以及相应的算法一、隐马尔可夫模型(Hidden Markov Model, HMM)隐马尔可夫模型是一种统计模型,它描述由一个隐藏的马尔可夫链随机生成的不可观测的状态序列,再由各个状态生成一个观测而产生观测序列的过程。
HMM广泛应用于语音识别、自然语言处理、生物信息学等领域。
二、三个基本问题1. 概率计算问题(Forward-Backward算法)给定模型λ=(A,B,π)和观察序列O=(o1,o2,…,oT),计算在模型λ下观察序列O出现的概率P(O|λ)。
解法:前向-后向算法(Forward-Backward algorithm)。
前向算法计算从t=1到t=T时,状态为i且观察值为o1,o2,…,ot的概率;后向算法计算从t=T到t=1时,状态为i且观察值为ot+1,ot+2,…,oT的概率。
最终将两者相乘得到P(O|λ)。
2. 学习问题(Baum-Welch算法)给定观察序列O=(o1,o2,…,oT),估计模型参数λ=(A,B,π)。
解法:Baum-Welch算法(EM算法的一种特例)。
该算法分为两步:E 步计算在当前模型下,每个时刻处于每个状态的概率;M步根据E步计算出的概率,重新估计模型参数。
重复以上两步直至收敛。
3. 预测问题(Viterbi算法)给定模型λ=(A,B,π)和观察序列O=(o1,o2,…,oT),找到最可能的状态序列Q=(q1,q2,…,qT),使得P(Q|O,λ)最大。
解法:Viterbi算法。
该算法利用动态规划的思想,在t=1时初始化,逐步向后递推,找到在t=T时概率最大的状态序列Q。
具体实现中,使用一个矩阵delta记录当前时刻各个状态的最大概率值,以及一个矩阵psi记录当前时刻各个状态取得最大概率值时对应的前一时刻状态。
最终通过回溯找到最可能的状态序列Q。
三、相应的算法1. Forward-Backward算法输入:HMM模型λ=(A,B,π)和观察序列O=(o1,o2,…,oT)输出:观察序列O在模型λ下出现的概率P(O|λ)过程:1. 初始化:$$\alpha_1(i)=\pi_ib_i(o_1),i=1,2,…,N$$2. 递推:$$\alpha_t(i)=\left[\sum_{j=1}^N\alpha_{t-1}(j)a_{ji}\right]b_i(o_t),i=1,2,…,N,t=2,3,…,T$$3. 终止:$$P(O|λ)=\sum_{i=1}^N\alpha_T(i)$$4. 后向算法同理,只是从后往前递推。
数学之美之隐马尔可夫模型刚开始学习此类知识,好多模型、算法都还待了解,看到google研究员的数学之美系列有不少模型算法介绍,拿来摘下,虽然没有⾃⼰的东西,但是希望能⾃⼰能在这⾥留的时间长⼀点,21天可以⼀个习惯,权当开个头,希望今后能有⾃⼰的东西。
原⽂:,1.马尔可夫模型的假设如果 S 表⽰⼀连串特定顺序排列的词 w1, w2,…, wn ,换句话说,S 可以表⽰某⼀个由⼀连串特定顺序排练的词⽽组成的⼀个有意义的句⼦。
现在,机器对语⾔的识别从某种⾓度来说,就是想知道S在⽂本中出现的可能性,也就是数学上所说的S 的概率⽤ P(S) 来表⽰。
利⽤条件概率的公式,S 这个序列出现的概率等于每⼀个词出现的概率相乘,于是P(S) 可展开为:P(S) = P(w1)P(w2|w1)P(w3| w1 w2)…P(wn|w1 w2…wn-1)其中 P (w1) 表⽰第⼀个词w1 出现的概率;P (w2|w1) 是在已知第⼀个词的前提下,第⼆个词出现的概率;以次类推。
不难看出,到了词wn,它的出现概率取决于它前⾯所有词。
从计算上来看,各种可能性太多,⽆法实现。
因此我们假定任意⼀个词wi的出现概率只同它前⾯的词 wi-1 有关(即马尔可夫假设),于是问题就变得很简单了。
现在,S 出现的概率就变为:P(S) = P(w1)P(w2|w1)P(w3|w2)…P(wi|wi-1)…(当然,也可以假设⼀个词⼜前⾯N-1个词决定,模型稍微复杂些。
)接下来的问题就是如何估计 P (wi|wi-1)。
现在有了⼤量机读⽂本后,这个问题变得很简单,只要数⼀数这对词(wi-1,wi) 在统计的⽂本中出现了多少次,以及 wi-1 本⾝在同样的⽂本中前后相邻出现了多少次,然后⽤两个数⼀除就可以了,P(wi|wi-1) = P(wi-1,wi)/ P (wi-1)。
2.隐马尔可夫模型在语⾔处理中的应⽤其中 s1,s2,s3...表⽰信息源发出的信号。
隐马尔可夫模型基因序列隐马尔可夫模型(Hidden Markov Model,HMM)是一种统计模型,用于描述一个含有隐含未知参数的马尔可夫过程。
在基因序列分析中,隐马尔可夫模型常用于建模基因序列中的模式和特征。
以下是使用隐马尔可夫模型进行基因序列分析的一般步骤:1. 模型建立:- 定义状态:将基因序列中的各个位置或区域定义为状态。
例如,可以将每个碱基(A、C、G、T)定义为一个状态。
- 定义转移概率:确定在不同状态之间转移的概率。
这些转移概率表示从一个状态转移到另一个状态的可能性。
通常,转移概率是根据训练数据或先验知识估计得到的。
- 定义发射概率:确定从每个状态发射出特定碱基的概率。
发射概率表示在某个状态下产生特定碱基的可能性。
同样,这些发射概率通常是根据训练数据或先验知识估计得到的。
2. 模型训练:- 收集训练数据:使用已知的基因序列作为训练数据。
这些训练数据可以来自公共数据库或实验获得的基因序列。
- 估计参数:根据训练数据,通过最大似然估计或其他方法来估计隐马尔可夫模型的参数,包括转移概率和发射概率。
- 优化模型:根据估计的参数,对模型进行优化,以提高其对训练数据的拟合能力。
3. 模型应用:- 序列预测:利用训练好的隐马尔可夫模型,对新的基因序列进行预测。
根据模型的参数,可以预测出序列中每个位置最可能的状态或碱基。
- 特征提取:隐马尔可夫模型可以用于提取基因序列中的特征。
通过分析模型的状态和转移概率,可以发现序列中的模式和特征。
需要注意的是,隐马尔可夫模型在基因序列分析中有一些局限性,例如模型的准确性和可靠性可能受到训练数据的数量和质量的影响。
此外,隐马尔可夫模型通常是一种概率模型,它提供的是序列的概率分布,而不是确定性的预测。
在实际应用中,可以结合其他生物信息学工具和方法,如序列比对、基因注释和功能分析,来综合评估和解释基因序列的特征和意义。
隐马尔可夫模型的原理隐马尔可夫模型(Hidden Markov Model,HMM)是一种用于建模时序数据的统计模型。
它在许多领域中都有广泛的应用,如语音识别、自然语言处理、生物信息学等。
本文将介绍隐马尔可夫模型的原理及其应用。
一、隐马尔可夫模型的基本概念隐马尔可夫模型由两个基本部分组成:状态序列和观测序列。
状态序列是一个随机变量序列,表示系统在不同时间点的状态;观测序列是与状态序列对应的观测值序列,表示在每个时间点观测到的数据。
隐马尔可夫模型的基本假设是马尔可夫性质,即当前状态只与前一个状态有关,与其他状态和观测无关。
这一假设使得隐马尔可夫模型具有简洁的表示和高效的计算。
二、隐马尔可夫模型的三个问题在隐马尔可夫模型中,有三个基本问题需要解决:状态序列问题、观测序列概率计算问题和参数估计问题。
1. 状态序列问题给定模型参数和观测序列,状态序列问题是要求找到最可能的状态序列。
这可以通过动态规划算法中的维特比算法来解决。
2. 观测序列概率计算问题给定模型参数和观测序列,观测序列概率计算问题是要求计算给定观测序列的概率。
这可以通过前向算法或后向算法来解决。
3. 参数估计问题给定观测序列,参数估计问题是要求估计模型参数。
这可以通过Baum-Welch算法(也称为EM算法)来解决。
三、隐马尔可夫模型的应用隐马尔可夫模型在许多领域中都有广泛的应用。
1. 语音识别隐马尔可夫模型在语音识别中被广泛应用。
语音信号可以看作是状态序列,而观测序列是对应的声学特征。
通过训练隐马尔可夫模型,可以实现对语音信号的识别和理解。
2. 自然语言处理隐马尔可夫模型在自然语言处理中也有重要的应用。
例如,可以将自然语言文本看作是状态序列,而观测序列是对应的词语或字符。
通过训练隐马尔可夫模型,可以实现对自然语言文本的分词、词性标注等任务。
3. 生物信息学隐马尔可夫模型在生物信息学中也有广泛的应用。
例如,可以将DNA 序列看作是状态序列,而观测序列是对应的碱基。