【最新】隐马尔科夫模型

隐马尔可夫模型参数估计
隐马尔可夫模型参数估计是指在隐马尔可夫模型中，根据观
测数据估计模型参数的过程。

隐马尔可夫模型是一种概率模型，
它用来描述一个隐藏状态序列的概率分布，它可以用来描述一个
隐藏状态序列的概率分布，以及它们之间的转移概率。

隐马尔可
夫模型参数估计是一个复杂的过程，它需要根据观测数据来估计
模型参数，以便更好地描述隐藏状态序列的概率分布。

隐马尔可夫模型参数估计的方法有很多，其中最常用的是最
大似然估计法。

最大似然估计法是一种概率模型参数估计的方法，它的基本思想是，根据观测数据，求出使得观测数据出现的概率
最大的模型参数。

另外，还有一些其他的参数估计方法，比如最
小二乘法、最小化KL散度等。

隐马尔可夫模型参数估计的结果可以用来描述隐藏状态序列
的概率分布，以及它们之间的转移概率。

此外，它还可以用来预
测未来的状态，以及推断未知的状态。

因此，隐马尔可夫模型参
数估计是一个非常重要的过程，它可以帮助我们更好地理解隐藏
状态序列的概率分布，以及它们之间的转移概率。

HMM隐马尔可夫模型在自然语言处理中的应用隐马尔可夫模型（Hidden Markov Model，HMM）是自然语言处理中常用的一种概率统计模型，它广泛应用于语音识别、文本分类、机器翻译等领域。

本文将从HMM的基本原理、应用场景和实现方法三个方面，探讨HMM在自然语言处理中的应用。

一、HMM的基本原理HMM是一种二元组（ $λ=(A,B)$），其中$A$是状态转移矩阵，$B$是观测概率矩阵。

在HMM中，状态具有时序关系，每个时刻处于某一状态，所取得的观测值与状态相关。

具体来说，可以用以下参数描述HMM模型：- 隐藏状态集合$S={s_1,s_2,...,s_N}$：表示模型所有可能的状态。

- 观测符号集合$V={v_1,v_2,...,v_M}$：表示模型所有可能的观测符号。

- 初始状态分布$\pi={\pi (i)}$：表示最初处于各个状态的概率集合。

- 状态转移矩阵$A={a_{ij}}$：表示从$i$状态转移到$j$状态的概率矩阵。

- 观测概率矩阵$B={b_j(k)}$：表示处于$j$状态时，观测到$k$符号的概率。

HMM的主要任务是在给定观测符号序列下，求出最有可能的对应状态序列。

这个任务可以通过HMM的三种基本问题求解。

- 状态序列概率问题：已知模型参数和观测符号序列，求得该观测符号序列下各个状态序列的概率。

- 观测符号序列概率问题：已知模型参数和状态序列，求得该状态序列下观测符号序列的概率。

- 状态序列预测问题：已知模型参数和观测符号序列，求得使得观测符号序列概率最大的对应状态序列。

二、HMM的应用场景1. 语音识别语音识别是指将语音信号转化成文字的过程，它是自然语言处理的关键技术之一。

HMM在语音识别领域具有广泛应用，主要用于建立声学模型和语言模型。

其中，声学模型描述语音信号的产生模型，是从语音输入信号中提取特征的模型，而语言模型描述语言的组织方式，是指给定一个句子的前提下，下一个字或单词出现的可能性。

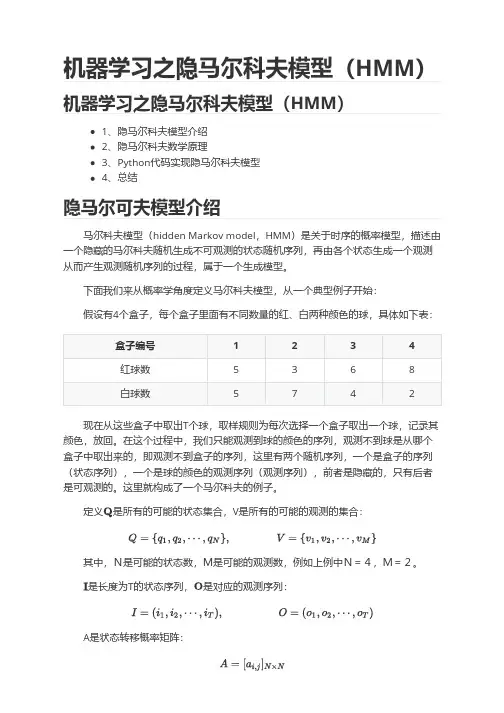
机器学习之隐马尔科夫模型（HMM）机器学习之隐马尔科夫模型（HMM）1、隐马尔科夫模型介绍2、隐马尔科夫数学原理3、Python代码实现隐马尔科夫模型4、总结隐马尔可夫模型介绍马尔科夫模型（hidden Markov model，HMM）是关于时序的概率模型，描述由一个隐藏的马尔科夫随机生成不可观测的状态随机序列，再由各个状态生成一个观测从而产生观测随机序列的过程，属于一个生成模型。

下面我们来从概率学角度定义马尔科夫模型，从一个典型例子开始：假设有4个盒子，每个盒子里面有不同数量的红、白两种颜色的球，具体如下表：盒子编号1234红球数5368白球数5742现在从这些盒子中取出T个球，取样规则为每次选择一个盒子取出一个球，记录其颜色，放回。

在这个过程中，我们只能观测到球的颜色的序列，观测不到球是从哪个盒子中取出来的，即观测不到盒子的序列，这里有两个随机序列，一个是盒子的序列（状态序列），一个是球的颜色的观测序列（观测序列），前者是隐藏的，只有后者是可观测的。

这里就构成了一个马尔科夫的例子。

定义是所有的可能的状态集合，V是所有的可能的观测的集合：其中，Ｎ是可能的状态数，Ｍ是可能的观测数，例如上例中Ｎ＝４，Ｍ＝２。

是长度为T的状态序列，是对应的观测序列：A是状态转移概率矩阵：其中，　是指在时刻处于状态的条件下在时刻转移到状态的概率。

B是观测概率矩阵：其中，　是指在时刻处于状态的条件下生成观测的概率。

是初始状态概率向量：其中，　是指在时刻=1处于状态的概率。

由此可得到，隐马尔可夫模型的三元符号表示，即称为隐马尔可夫模型的三要素。

由定义可知隐马尔可夫模型做了两个基本假设：(1)齐次马尔科夫性假设，即假设隐藏的马尔科夫链在任意时刻的状态只和-1状态有关；(2)观测独立性假设，观测只和当前时刻状态有关；仍以上面的盒子取球为例，假设我们定义盒子和球模型：状态集合： = {盒子1，盒子2，盒子3，盒子4}， N=4观测集合： = {红球，白球} M=2初始化概率分布：状态转移矩阵：观测矩阵:（1）转移概率的估计：假设样本中时刻t处于状态i，时刻t+1转移到状态j 的频数为那么转台转移概率的估计是：（2）观测概率的估计：设样本中状态为j并观测为k的频数是那么状态j观测为k的概率，　（3）初始状态概率的估计为S个样本中初始状态为的频率。

隐藏式马尔可夫模型及其应用随着人工智能领域的快速发展，现在越来越多的数据需要被处理。

在这些数据中，有些数据是难以被观察到的。

这些难以被观察到的数据我们称之为“隐藏数据”。

如何对这些隐藏数据进行处理和分析，对于我们对这些数据的认识和使用有着至关重要的影响。

在这种情况下，隐马尔可夫模型就显得非常重要了。

隐马尔可夫模型（Hidden Markov Model，HMM）是一种非常重要的统计模型，它是用于解决许多实际问题的强有力工具。

该模型在语音识别、自然语言处理、生物信息学、时间序列分析等领域都有广泛应用。

隐马尔可夫模型是一种基于概率的统计模型。

该模型涉及两种类型的变量：可见变量和隐藏变量。

可见变量代表我们能够观察到的序列，隐藏变量代表导致可见序列生成的隐性状态序列。

HMM 的应用场景非常广泛，如基因组序列分析、语音识别、自然语言处理、机器翻译、股票市场等。

其中，最常见和经典的应用场景之一是语音识别。

在语音识别过程中，我们需要将输入的声音转换成文本。

这里，语音信号是一个可见序列，而隐藏变量则被用来表示说话人的音高调整、语速变化等信息。

HMM 的训练过程旨在确定模型的参数，以使得模型能够最佳地描述观察到的数据。

在模型训练中，需要对模型进行无监督地训练，即：模型的训练样本没有类别信息。

这是由于在大多数应用场景中，可收集到的数据往往都是无标注的。

在语音识别的任务中，可以将所需的标签（即对应文本）与音频文件一一对应，作为主要的训练数据。

我们可以利用EM算法对模型进行训练。

EM算法是一种迭代算法，用于估计最大似然和最大后验概率模型的参数。

每次迭代的过程中使用E步骤计算期望似然，并使用M步骤更新参数。

在E步骤中，使用当前参数计算隐藏状态的后验概率。

在M步中，使用最大似然或者最大后验概率的方法计算参数更新值。

这个过程一直进行到模型参数收敛为止。

总的来说，隐马尔可夫模型是一种非常强大的工具，能够应用于许多领域。

隐马尔可夫模型的应用必须细心，仔细考虑数据预处理、模型参数的选择和训练等问题。

神经网络人工神经网络（Artificial Neural Networks，简写为ANNs）也简称为神经网络（NNs）或称作连接模型（Connection Model），它是一种模范动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。

这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。

隐马尔可夫模型隐马尔可夫模型（Hidden Markov Model，HMM）作为一种统计分析模型，创立于20世纪70年代。

80 年代得到了传播和发展，成为信号处理的一个重要方向，现已成功地用于语音识别，行为识别，文字识别以及故障诊断等领域。

隐马尔可夫模型是马尔可夫链的一种，它的状态不能直接观察到，但能通过观测向量序列观察到，每个观测向量都是通过某些概率密度分布表现为各种状态，每一个观测向量是由一个具有相应概率密度分布的状态序列产生。

所以，隐马尔可夫模型是一个双重随机过程----具有一定状态数的隐马尔可夫链和显示随机函数集。

自20世纪80年代以来，HMM被应用于语音识别，取得重大成功。

到了90年代，HMM还被引入计算机文字识别和移动通信核心技术“多用户的检测”。

近年来，HMM在生物信息科学、故障诊断等领域也开始得到应用。

1. 评估问题。

给定观测序列O=O1O2O3…Ot和模型参数λ=(A,B,π)，怎样有效计算某一观测序列的概率，进而可对该HMM做出相关评估。

例如，已有一些模型参数各异的HMM，给定观测序列O=O1O2O3…Ot，我们想知道哪个HMM模型最可能生成该观测序列。

通常我们利用forward算法分别计算每个HMM 产生给定观测序列O的概率，然后从中选出最优的HMM模型。

这类评估的问题的一个经典例子是语音识别。

在描述语言识别的隐马尔科夫模型中，每个单词生成一个对应的HMM，每个观测序列由一个单词的语音构成，单词的识别是通过评估进而选出最有可能产生观测序列所代表的读音的HMM而实现的。

隐马尔科夫模型在城市规划中的应用案例引言隐马尔科夫模型（Hidden Markov Model, HMM）是一种用来描述具有隐藏状态的动态系统的概率模型。

它在语音识别、自然语言处理、生物信息学等领域有着广泛的应用。

在城市规划领域，隐马尔科夫模型也被广泛应用，以解决城市发展、交通规划、环境保护等方面的问题。

本文将通过介绍几个实际案例，探讨隐马尔科夫模型在城市规划中的应用。

案例一：城市人口增长预测隐马尔科夫模型可以通过对城市历史人口数据的分析，预测未来城市的人口增长趋势。

以某大城市为例，通过收集该城市过去几十年的人口数据，可以构建隐马尔科夫模型，以预测该城市未来的人口增长情况。

通过对历史数据的分析，可以确定不同年龄段人口的迁移情况，从而为城市规划者提供决策参考。

比如，预测未来的年龄结构变化，有助于规划城市的教育、医疗等公共服务设施。

案例二：交通流量预测隐马尔科夫模型也可以用于城市交通规划中。

通过收集城市道路交通历史数据，结合气象、节假日等因素，构建隐马尔科夫模型，可以预测城市不同时间段的交通流量。

这有助于规划城市交通信号灯、道路扩建、公共交通优化等项目。

比如，在高峰时段预测道路流量的增长，可以对交通拥堵进行有效的管控，提高城市交通效率。

案例三：环境污染分析城市环境保护是当前社会关注的焦点之一。

隐马尔科夫模型可以用于分析城市环境污染情况。

通过对城市空气质量、水质等环境数据的收集，构建隐马尔科夫模型，可以预测城市环境污染的发展趋势。

这对于城市规划者来说是非常重要的信息，可以帮助他们制定环境保护政策，改善城市环境质量。

案例四：城市用地规划隐马尔科夫模型还可以用于城市用地规划。

通过对城市不同地区的历史数据进行分析，可以构建隐马尔科夫模型，预测不同地区未来的发展趋势。

这有助于城市规划者合理规划土地资源利用，避免土地浪费和不合理利用。

结论隐马尔科夫模型在城市规划中的应用案例丰富多样，涵盖了人口增长预测、交通流量预测、环境污染分析、城市用地规划等多个方面。

数据分析中的马尔可夫链和隐马尔可夫模型数据分析是当今信息时代中一项重要的技术，通过对海量的数据进行统计和分析，可以从中挖掘出有用的信息和规律，对各个领域产生积极的影响。

而在数据分析中，马尔可夫链和隐马尔可夫模型是两个常用的工具，具有很高的应用价值。

一、马尔可夫链马尔可夫链（Markov chain）是一种随机过程，具有"无记忆性"的特点。

它的特殊之处在于，当前状态只与前一个状态相关，与更早的各个状态无关。

这种特性使马尔可夫链可以被广泛应用于许多领域，如自然语言处理、金融市场预测、天气预测等。

在数据分析中，马尔可夫链可以用来建模和预测一系列随机事件的发展趋势。

通过观察历史数据，我们可以计算不同状态之间的转移概率，然后利用这些转移概率进行状态预测。

以天气预测为例，我们可以根据历史数据得到不同天气状态之间的转移概率，从而预测未来几天的天气情况。

二、隐马尔可夫模型隐马尔可夫模型（Hidden Markov Model，HMM）是马尔可夫链的扩展形式。

在隐马尔可夫模型中，系统的状态是隐含的，我们只能通过观察到的一系列输出来推测系统的状态。

隐马尔可夫模型在很多领域中都有广泛的应用，尤其是语音识别、自然语言处理、生物信息学等方面。

以语音识别为例，输入的语音信号是可观察的输出，而对应的语音识别结果是隐藏的状态。

通过对大量的语音数据进行训练，我们可以得到不同状态之间的转移概率和观测概率，从而在实时的语音输入中进行识别和预测。

三、马尔可夫链和隐马尔可夫模型的应用案例1. 金融市场预测马尔可夫链和隐马尔可夫模型可以应用于金融市场的预测。

通过建立模型，我们可以根据历史数据预测未来的市场状态。

例如，在股票交易中，我们可以根据过去的价格走势来预测未来的股价涨跌情况，以辅助决策。

2. 自然语言处理在自然语言处理领域，马尔可夫链和隐马尔可夫模型经常被用来进行文本生成、机器翻译等任务。

通过对大量文本数据的学习，我们可以构建一个语言模型，用于生成符合语法和语义规则的句子。

隐马尔可夫模型三个基本问题及算法隐马尔可夫模型(Hien Markov Model, HMM)是一种用于建模具有隐藏状态和可观测状态序列的概率模型。

它在语音识别、自然语言处理、生物信息学等领域广泛应用，并且在机器学习和模式识别领域有着重要的地位。

隐马尔可夫模型有三个基本问题，分别是状态序列概率计算问题、参数学习问题和预测问题。

一、状态序列概率计算问题在隐马尔可夫模型中，给定模型参数和观测序列，计算观测序列出现的概率是一个关键问题。

这个问题通常由前向算法和后向算法来解决。

具体来说，前向算法用于计算给定观测序列下特定状态出现的概率，而后向算法则用于计算给定观测序列下前面状态的概率。

这两个算法相互协作，可以高效地解决状态序列概率计算问题。

二、参数学习问题参数学习问题是指在给定观测序列和状态序列的情况下，估计隐马尔可夫模型的参数。

通常采用的算法是Baum-Welch算法，它是一种迭代算法，通过不断更新模型参数来使观测序列出现的概率最大化。

这个问题的解决对于模型的训练和优化非常重要。

三、预测问题预测问题是指在给定观测序列和模型参数的情况下，求解最可能的状态序列。

这个问题通常由维特比算法来解决，它通过动态规划的方式来找到最可能的状态序列，并且在很多实际应用中都有着重要的作用。

以上就是隐马尔可夫模型的三个基本问题及相应的算法解决方法。

在实际应用中，隐马尔可夫模型可以用于许多领域，比如语音识别中的语音建模、自然语言处理中的词性标注和信息抽取、生物信息学中的基因预测等。

隐马尔可夫模型的强大表达能力和灵活性使得它成为了一个非常有价值的模型工具。

在撰写这篇文章的过程中，我对隐马尔可夫模型的三个基本问题有了更深入的理解。

通过对状态序列概率计算问题、参数学习问题和预测问题的深入探讨，我认识到隐马尔可夫模型在实际应用中的重要性和广泛适用性。

隐马尔可夫模型的算法解决了许多实际问题，并且在相关领域有着重要的意义。

隐马尔可夫模型是一种强大的概率模型，它的三个基本问题和相应的算法为实际应用提供了重要支持。