当前位置：文档之家 › 第九章 分布滞后模型

第九章 分布滞后模型

  • 格式：ppt
  • 大小：1.18 MB
  • 文档页数：54

下载文档原格式

  / 54

合集下载

分布滞后模型的估计

分布滞后模型的估计

分布滞后模型的估计建立总量消费函数是进行宏观经济管理的重要手段。

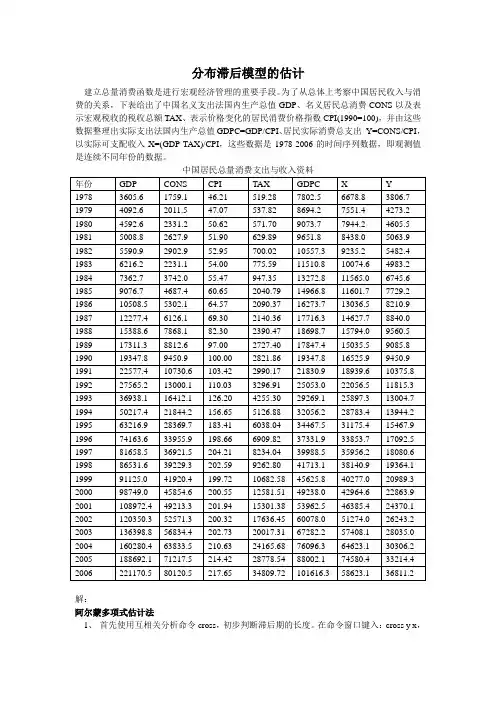
为了从总体上考察中国居民收入与消费的关系，下表给出了中国名义支出法国内生产总值GDP、名义居民总消费CONS以及表示宏观税收的税收总额TAX、表示价格变化的居民消费价格指数CPI(1990=100)，并由这些数据整理出实际支出法国内生产总值GDPC=GDP/CPI、居民实际消费总支出Y=CONS/CPI，以实际可支配收入X=(GDP-TAX)/CPI，这些数据是1978-2006的时间序列数据，即观测值是连续不同年份的数据。

中国居民总量消费支出与收入资料解：阿尔蒙多项式估计法1、首先使用互相关分析命令cross，初步判断滞后期的长度。

在命令窗口键入：cross y x，输出结果如下图所示：x与y各期滞后值的相关系数从上图中可以看出，消费总支出y与当年和前四年的实际可支配收入相关，因此，利用阿尔蒙多项式估计法估计模型时，解释变量滞后阶数为5.利用EViews软件，输入样本数据，在命令窗口键入：LS y c pdl(x,5,2)得到以下回归分析结果：估计结果：xx x x x x yt t t t t t t5432104497.010270.013208.013311.010580.005015.0192.1794-----∧+++---= t = (2.07755) (6.63411) (6.51267) (7.90985) (6.26776) (0.99479)997444.02=R，250.2471=F ，955959.0..=W D其中括号内的数为相应参数的T 检验，R2是可决系数，F 和D.W.是有关的两个检验统计量。

2、模型检验从回归估计和残差图可以看出模型的拟合程度较好。

从截距项与斜率项的t 检验值看，均大于5%显著性水平下自由度为n-2=27的临界值052.2)27(025,0 t，认为中国总量消费与支出以及与各滞后消费间线性相关性显著，并且解释变量间不存在多重共线性。

9 分布滞后模型

9 分布滞后模型

9.120033
9.218058 2601.407 0.000000
8.2
有限分布滞后模型及其估计
Dependent Variable: Y
Method: Least Squares Sample(adjusted): 1958 1974 Included observations: 17 after adjusting endpoints Variable C Z2 R-squared Adjusted R-squared S.E. of regression Sum squared resid Coefficient -133.0331 1.366409 0.989328 0.988617 29.86519 13378.94 Std. Error 26.53012 0.036642 t-Statistic -5.014417 37.29030 Prob. 0.0002 0.0000 818.6959 279.9181 9.741395 9.839420
分别估计如下经验加权模型：
yt a bzkt ut
8.2
有限分布滞后模型及其估计
Dependent Variable: Y Method: Least Squares Sample(adjusted): 1958 1974 Included observations: 17 after adjusting endpoints Variable Coefficient Std. Error t-Statistic Prob.
Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion
Log likelihood

第九章 滞后变量模型复习

第九章 滞后变量模型复习

6. 根据某行业1991-2010年的库存量Y和销售量X的资料， 运用EViews软件得如下资料，试根据所给资料完成下列 问题 （1）填写表1空白处的数值 （2）用标准书写格式写出估计模型的表达式 （3）求库存量Y对销售量X的短期乘数、动态乘数和长期 乘数，同时给出经济解释 （4）根据所给资料对估计模型进行评价（包括经济意义、 拟合效果、显著性检验等）
5．产生滞后现象的原因有哪些？
答：主要是由于经济变量自身、决策者心里、技术和制度的原因。
6．Koyck变换的意义是什么？
答：Koyck变换将无限分布滞后模型变换成只有Xt和Yt-1的一阶自回 归模型，模型结构极大简化，最大限度保留了自由度，解决的滞后 长度难以确定的问题，Xt和Yt-1的线性相关程度将低于X各期值之间 的线性相关程度，降低了多重共线性。
三、判断题
1、× 6、√ 11、× 2、× 7、× 12、√ 3、× 8、× 13、√ 4、√ 9、√ 5、× 10、√ 14、×
7．Koyck变换模型、自适应预期模型和局部调整模型有何 异同？模型估计会遇到什么困难？怎样解决？
答：三种模型的最终形式都是一阶自回归模型。区别：一是导出 模型的经济背景和思想不同，二是由于模型形成机制不同导致模 型的随机扰动项的结构不同。模型存在随机解释变量问题，并且 由于模型的随机扰动项的结构不同，给模型估计带来了问题，局 部调整模型存在异期相关问题，用OLS法就可得到一致性估计， Koyck变换模型和自适应预期模型同期相关问题，需要用工具变 量法得到一致性估计。
构造F统计量：
( RSS R RSSU ) m F RSSu nk
四、简答题
1．滞后变量模型的作用是什么？
答：（1）滞后变量模型可以更全面、客观的描述经济现象，提高模 型的拟合优度。 （2）滞后变量模型可以反映过去的经济活动对现期的经济行为的影 响，从而描述经济活动的运动过程，使模型成为动态模型。 （3）滞后变量模型可以模拟分析经济过程的变化调整过程。

分布滞后模型

分布滞后模型



7
1.有限分布滞后模型的最大滞后长度s 较难确定。其 确定往往带有主观随意性。 2.如果滞后期较长而样本较小时，就没有足够的自 由度进行统计推断。 因为，每增加一个解释变量就会失去一个自由度。 同时，滞后期每增加一期，可利用的数据就会减 少一个。 3. 时间序列资料中，大多存在序列相关问题（如Xt-1 与Xt-2）。在分布滞后模型中，这种序列相关问题就 转化为解释变量之间的多重共线性问题。
3
1、分布滞后模型 分布滞后模型形式为：
Yt 0 X t 1 X t 1 s X t s ut
或
Yt 0 X t 1 X t 1 ut
其中第一式的最大滞后长度 s是一个确定的数，因 此是有限分布滞后模型。 而第二式没有规定最大滞后长度，是无限分布滞后 模型。
称为长期乘数或总分布乘数，它表示滞后效应 对 Y 总的影响；
5
2、自回归模型 自回归模型形式为：
Yt 0 Xt 1Yt 1 2Yt 2 qYt q ut
其中，q 称为自回归模型的阶数。
6
第二节 分布滞后模型的估计
一、分布滞后模型的估计难度
直接应用最小二乘法估计分布滞后模型会遇到很 多困难。 由于无限分布滞后模型中包含无限多个参数，我 们无法用最小二乘法对其进行估计。 对于有限分布滞后模型，最小二乘法原则上是适 用的，但在具体应用时会遇到很多困难。
i 0,1,2,, s
此式称为Almon多项式变换。
多项式的阶数 m 必须小于有限分布滞后模型的最 大滞后长度 s ，否则就达不到减少参数个数的目的。 在具体应用时，m 一般取 2 或 3，不超过 4。 具体列出来就是:
0 0 1 0 2 02 m 0m 2 m 1 1 1 1 0 1 2 m 2 m s s s 0 1 2 m s

第九章分布滞后和自回归模型

第九章分布滞后和自回归模型



i a0 a1i 当m 1时，即： 2 当m 2 时，即： i a0 a1i a2i 等。其余依次类推。 不难看出，阿尔蒙多项式所设定的滞后 参数变化模式，根据所选择的多项式次 数m的不同，分别对应线性变化（衰 减），先增后减的二次函数变化，以及 较复杂的高次曲线变化等。衰减速度则 a1 等参数。 取决于a0 、


从另一个角度，滞后效应也可以反过来 理解为当期某指标受上期、再上期其他 某指标的影响。 例如上述消费滞后效应也可理解为，当 年消费不仅受到当年收入（40%）的影 响，而且受到上年收入（30%）、再上 年收入（20%）的影响。用公式表示就 是： Ct 0.4It 0.3It 1 0.2It 2

ቤተ መጻሕፍቲ ባይዱ
这种分布滞后模型的参数估计方法就是现式估 计法。这种参数估计方法只是普通最小二乘估 计的重复应用，易于掌握。 但现式估计法也有问题。首先滞后长度的确定 没有明确的标准、根据；其次是引进较多期滞 后会降低自由度，回归分析的有效性会降低； 第三是滞后变量之间的相关性可能引发共线性 问题；此外被认为有数据开采的嫌疑。
第九章 分布滞后和自回归模型
前言



前面各章基本上没有区别所用的数据究竟是时 间序列数据还是截面数据。但这两类数据在计 量经济分析中还是有明显差异的。 时间序列数据是经济运动动态过程的数量记录， 包含不同于横截面数据的特殊信息，可以进行 动态计量分析，但时间序列数据的内在联系也 可能给计量经济分析带来问题和困难。 本章介绍利用时间序列数据进行动态计量分析 的几个专题。下一章我们将对时间序列数据计 量分析的一些问题进行分析。



其次是滞后效应的模式，对应于m，也 必须预先知道，这就很难以避免判断的 主观偏差。 最后上述变量变换会缩短样本长度，因 此并不能完全解决分布滞后模型参数估 计的自由度问题。 当样本容量并不是很大，滞后期长度较 长时，仍然无法得到有效的估计结果。

第九章 案例分析(分布滞后模型)

第九章 案例分析(分布滞后模型)

第九章 案例分析【案例7.1】 为了研究1955—1974年期间美国制造业库存量Y 和销售额X 的关系，用阿尔蒙法估计如下有限分布滞后模型：tt t t t t u X X X X Y +++++=---3322110ββββα将系数i β(i =0,1,2,3)用二次多项式近似，即00αβ=2101αααβ++=210242αααβ++=210393αααβ++=则原模型可变为t t t t t u Z Z Z Y ++++=221100αααα其中3212321132109432---------++=++=+++=t t t t t t t t t t t t t X X X Z X X X Z X X X X Z在Eviews 工作文件中输入X 和Y 的数据，在工作文件窗口中点击“Genr ”工具栏，出现对话框，输入生成变量Z 0t 的公式，点击“OK ”；类似，可生成Z 1t 、Z 2t 变量的数据。

进入Equation Specification 对话栏，键入回归方程形式Y C Z0 Z1 Z2点击“OK ”，显示回归结果（见表7.2）。

表7.2表中Z0、 Z1、Z2对应的系数分别为210ααα、、的估计值210ˆˆˆααα、、。

将它们代入分布滞后系数的阿尔蒙多项式中，可计算出3210ˆˆˆˆββββ、、、的估计值为：-0.522)432155.0(9902049.03661248.0ˆ9ˆ3ˆˆ0.736725)432155.0(4902049.02661248.0ˆ4ˆ2ˆˆ 1.131142)432155.0(902049.0661248.0ˆˆˆˆ661248.0ˆˆ21012101210100=-⨯+⨯+=++==-⨯+⨯+=++==-++=++===αααβαααβαααβαβ从而，分布滞后模型的最终估计式为：32155495.076178.015686.1630281.0419601.6----+++-=t t t t t X X X X Y在实际应用中，Eviews 提供了多项式分布滞后指令“PDL ”用于估计分布滞后模型。

第九章 滞后模型

第九章 滞后模型

第九章 滞后变量回归模型回归分析经常遇到时间序列资料，如果在回归模型中不仅含有解释变量X 的当前值而且含有X 的滞后值，它就称为分布滞后模型(Distributed-Lag Model)，如t t t t t X X X Y εβββα++++=--221100（9.0.1）就是一个分布滞后模型。

如果模型中包含一个或若干个因变量的滞后值，它就称为自回归模型(Autoregressive Model)，如t t t t Y X Y εγβα+++=-1（9.0.2）就是一个自回归模型。

分布滞后模型与自回归模型都属于滞后变量回归模型，它在经济领域有广泛的应用。

一个当前的经济指针，经常受到过去某些经济指针(包括自身的)影响，这是件很常见很容易理解的事情。

我们在处理这一类问题时要考虑下列问题：1．经济分析中滞后起什么作用? 2．滞后的原因是什么?3．在实证分析中对滞后有没有什么理论判别方法?4．自回归与分布滞后有什么关系?能否从一个导出另一个? 5．滞后变量模型中有哪一些统计问题?6．变量之间的滞后是否意味着灾难?如果是，如何度量它? 这些问题有些是不能给出精确定义或精确解答的，只可体会其意思。

我们以下主要是从经济模型的数学形式来展开讨论。

第一节 模型概念：消费滞后、通胀滞后与存款创生实际经济活动中，因变量Y 经常是与经济自变量的过去值有关，而与当前值有关反而少一些。

为了具体说明这种滞后关系，我们看一些实例。

1．消费滞后假如一个消费者从今年起每年工资增加2000元，并将持续一段时间。

他的消费行为将受到怎样的影响呢?一般来说，他不会把当年增加的收入全部花光。

很可能是，他把每增加的2000元当年花掉800元，第二年花掉600元，第三年花掉400元，余下的永久储蓄起来。

这样到第三年，他的消费增加额将是1800元。

这样的消费函数写下就是t t t t t X X X C Y ε++++=--212.03.04.0（9.1.1）这里Y 是消费开支，C 是常数，X 是收入。

09滞后变量模型的基本概念

09滞后变量模型的基本概念

（表示过去各个时期X每变动一个单位对Y平均变动的影响 ）
(或 ) 长期乘数
i 1 i i 1 i
s

（表示X变动一个单位对Y的总影响 ）
2、自回归模型：回归模型不仅含解释变量的即期值，
还含被解释变量的若干期滞后值。
Y X Y Y u
t 0 t 1 t 1 q t q
同乘以，得：
Yt 1 0 X t i ut 1
i i 1

（4）
（3）-（4）
二、自适应预期模型
在经济活动中，预期起着决定性作用。人们常根据他们对 某些经济变量未来走势的预期变动来改变自己的行为决策。 例如：生产取决于预期的销售； 投资取决于预期的利润； 长期利率取决于预期的短期利率于预期的通货膨胀 率之和 X 即影响被解释变量的因素不是Xt，而是预期值 t
u ut (1 )ut 1
* t
自适应预期模型特点：
1、以一个滞后因变量代替了预期值。 2、干扰项是一阶自相关，作为解释变量的滞后因 变量与随机干扰项不独立。
三、局部调整模型
局部调整模型是构造滞后变量模型的另一种方法。这种方法 早先是用来研究 物资贮备问题。例如，企业为了保证生产或 供应，必须保持一定的原材料贮备。 * Y 对于一定的产量或销售量Xt ，存在着预期的最佳库存 t
最后得长期货币流通需求量 模型的估计式为
ln Y 0.4669 0.333ln X 1.0781ln X
* t 1t
2t
货币流通量对长期利率的弹性，本期为-0.2401， 长期为-0.333。对工业企业存款的弹性本期为 0.7773，长期为1.0781。说明在经济体制下，工 业企业存款每增长1%，在本期的影响是货币流通 量增长0.773%，长期影响增长1.0781%。

第九章分布滞后和自回归模型

第九章分布滞后和自回归模型
这类模型的主要困难是参数数量较多，导致估 计困难。
基本思想：以滞后期i 的一个适当次数的多项
式，模拟分布滞后模型的系数。 可分别模拟单调下降、先升后降，以及循环变
化等不同的滞后效应类型。
设一个有限分布滞后模型为：
Yt 0 X t 1X t 1 K X t K t
也可以写成：
分布滞后模型形式上是含有解释变量滞后项的 多元回归模型。
但分布滞后模型主要用来研究经济变量作用的 时间滞后效应、长期影响，以及经济变量之间 的动态影响关系，可用于评价经济政策的中长 期效果，属于动态计量分析的范畴。
二、分布滞后模型参数估计
用分布滞后模型研究滞后效应，进行预测分析 和评估政策效果之前，先要估计模型中的未知 参数。
i0
i0
则模型变为：
i0
Yt a0Z0t a1Z1t a2Z2t t
很显然，上述 Z0t、Z1t和 Z2t 只是 X t及其各
期滞后的线性组合，因此仍是非随机的 或与误差项无关。
因此可用OLS法对该式进行参数估计，得 到估计值
最后，只需要把这些估计值代入滞后参数多项 式，就可以得到得到各个滞后参数的估计值：
这种现象就是滞后效应。滞后效应在经济问题 中是普遍存在的。
例如人们获得后通常不会立即全部花掉，而是 会在以后一个阶段分次花费，因此收入对人们 消费的影响往往有时间滞后和持续的影响。
滞后效应对经济问题的影响非常重要。要准确 把握经济关系，特别是长期动态关系，避免预 测和决策偏差，必须重视这种滞后效应。
从另一个角度，滞后效应也可以反过来 理解为当期某指标受上期、再上期其他 某指标的影响。
例如上述消费滞后效应也可理解为，当 年消费不仅受到当年收入（40%）的影 响，而且受到上年收入（30%）、再上 年收入（20%）的影响。用公式表示就 是：Ct 0.4It 0.3It1 0.2It2

分布滞后模型2

分布滞后模型2

L β α
ˆ = ˆ + kα + k2α ˆ1 ˆ2 k 0
2.应用阿尔蒙模型之前需要解决的问题
(1)如何确定滞后长度 k 可以结合统计量来检验 如何确定滞后长度 结合相关系数分析，计算因变量和自变量的各期相关 计 量 经 济 学 系 数，可以大致判断滞后期长度； 利用调整后的修正系数 R2 ，在模型中逐期增加滞 后变量，扩大滞后期长度，直到模型的修正拟合系数不 再增加为止；或者先取一个较长的滞后期，再逐渐剔除 滞后变量，缩短滞后期长度，直到模型修正的拟合系数 明显下降为止；
Yt = α + β0 Xt + β1Xt−1 +L+ βk Xt−k + εt = α + ∑βi Xt−i + εt
i=0 k
计 量 经 济 学
根据数学中的维尔斯特拉斯定理，阿尔蒙假定估计参数β可 用滞后长度i的一个适当高次的多项式逼近
根据数学中的维尔斯特拉斯定理，阿尔蒙假定βi可用i的 一个适当高次的多项式逼近
i=0
3
估计上面的方程，有下面的结果
ˆ Yt = −9152.012 + 0.5825Z0t +1.2231Z1t − 0.5446Z2t
t=
(3.4431) (2.4112)
(-3.1145)
3.进一步得到βi的系数
ˆ ˆ β0 = α0 = 0.5825
计 量 经 济 学
ˆ ˆ ˆ ˆ β1 = α0 +α1 +α2 = 0.5825 +1.2231− 0.5446 = 1.261 ˆ ˆ ˆ ˆ β2 = α0 + 2α1 + 4α2 = 0.5825 + 2 ×1.2231− 4 ×0.5446 = 0.8503

分布滞后模型(上)

分布滞后模型(上)
滞后效应及其原因
定义：因变量受到自身滞后Y(-1)或另一解释变量的前几期值X(-1) 影响的现象称为滞后效应。
表示前几期值Y(-1)、X(-2)的变量称为滞后变量。
举例1：消费函数。消费除了受本期收入影响之外，还受前1期，或前2期 收入的影响：
Ct=0+1Yt+2Yt-1+3Yt-2+t Yt-1，Yt-2为滞后变量
0 Xt 1Xt1 2 Xt2 ... s Xts t
0短期或即期乘数,表示本期X变化一单位对Y平均值的影响程 度。
i (i=1,2…,s)：动态乘数或延迟系数，表示各滞后期
s
X的变动对Y平均值影响的大小。
i 称为长期或均衡乘数，表示X变动一个单位，
举例2：投资函数。当年产出依赖于过去若干期内投资形成的固定资产。 YtIt=0+1It+2It-1+3It-2+tIt-1，It-2为滞后变量——投资回报周期
分布滞后模型（distributed-lag
m
o
d
e
l
）
定义：仅受解释变量X当期值及滞后期的影响。
s
Yt i X ti t i0
i0
由于滞后效应而形成的对Y平均值总影响的大小。
滞后变量X(-1)、X(-2)…X(-i)如何引入模型Y中？
能否运用传统OLS估计方法？
（1）没有先验准则确定滞后期长度； （2）如果滞后期较长，将缺乏足够的自由度； （3）滞后变量X(-1)、X(-2)…X(-i)高度相关；
OLS方法失效
改进思想：针对有限分布滞后期模型，通过阿尔蒙
变换，定义新变量，以减少解释变量个数，然后用 OLS法估计参数。 —— 降维思想

计量经济学第九章分布滞后和自回归模型

计量经济学第九章分布滞后和自回归模型
转变为纯粹的自回归模型或完全的分布滞后模型，因此 不做专门讨论。
自回归模型的理论导出
适应性预期（Adaptive expectation）模型
在某些实际问题中，因变量 Yt 并不取决于解释变量的当
前实际值
X
t
，而取决于X
t
的“预期水平”或“长期均衡水X
* t
平” 。
例如，家庭本期消费水平，取决于本期收入的预期值；
❖ 为了解决滞后长度不确定的困难，可以依次估计滞 后效应变量的一期滞后、二期滞后…当发现滞后变 量（加入的最多期滞后）的回归系数在统计上开始 变得不显著，或至少有一个变量的系数改变符号 （由正变负或由负变正）时，就不再增加滞后期， 把此前一个模型作为分布滞后模型的形式，相应参 数估计作为模型的参数估计。
市场上某种商品供求量，决定于本期该商品价格的均衡值。
因此，适应性预期模型最初表现形式是
Yt
0
1
X
* t
t
由于预期变量是不可实际观测的，往往作如下 适应性预期假定:
X
* t
X* t 1
(Xt
X
* t 1
)
其中：r为预期系数（coefficient of expectation）, 0r 1。
该式的经济含义为：“经济行为者将根据过去的 经验修改他们的预期”，即本期预期值的形成是一 个逐步调整过程，本期预期值的增量是本期实际值 与前一期预期值之差的一部分，其比例为r 。
这个假定还可写成：
X
* t
X t
(1
)
X
* t 1
将
X
* t
X t
(1
)
X
* t 1
代入

自回归与分布滞后模型

自回归与分布滞后模型

Yt Ｃ 0.4xt 0.3xt 1 0.2xt 2 ut
其中Y是消费量，X是收入
(17.1.1)
更一般的，我们可以写成:
Yt 0 xt 1xt 1 2 xt 2
β
k xt k ut
(17.1.2)
0 表示随着X一个单位的变化， Y均值的同期变化，
• 其中 Y = 对货币（实际现金余额）的需求 * X • =均衡、最优、预期的长期或正常利率 u t =误差项 •
• 方程(17.5.1) 设想，货币需求是预期（预测意义的）利 率的函数.
• 由于预期变量 X 不可直接观测，我们对预期的形成做如 下的设想： (17.5.2) • 其中 为 0 1 ,称期望系数（coefficient of expectation）。假设(17.5.2) 称适应性预期（adaptive expectation）或累进式期望（progressive expectation） 或错误中学习假设（error learning hypothesis）. • (17.5.2) 表明：人们每期都按变量的现期值 X t与前期期 望值 X t 1* 之间的差距的一个分数 去修改期望值。 .
• 表达式证明
t 1 ）/(1- ) 1 长期反应 （ 0 t期反应 0 / (1 ) 2
1 ln 2 2 t ln ln ln
平均滞后 • 假设所有的β
k
都是正的，则平均滞后有相关滞后的加权平均。扼要地 说，它是滞后加权平均时间。（类似于投资学中的久期） 考伊克模型：平均滞后=
*
• 将 (17.5.3) 代入 (17.5.1), 我们得到：
Yt 0 1 X t 1 X t 1 ut

第九章 分布滞后模型

第九章 分布滞后模型
Yt 0 X t 1 X t 1 2 X t 2 ut
可以假定滞后解释变量 X t 对被解释变量Y的影响随着 i 滞后期i的增加而按几何级数衰减。即滞后系数的衰 减服从某种公比小于1的几何级数：
i 0
i
,
0 1 ,
i 0,1, 2,
i
s
一个单位时，由于滞后效应而形成的对Y总的影响 大小。
i 0
2、自回归模型
如果滞后变量模型的解释变量仅包括自变量X的 当期值和被解释变量的若干期滞后值，即模 型形如
y t 0 x t 2 y t 1 p y t p t
则称这类模型为自回归模型，其中p称为自回 归模型的阶数。
二、产生滞后效应的原因 1、经济变量自身原因 ２、心理因素 在经济转型变革时期，人们往往由于心理定势， 而不能及时适应新的变化，表现为行为决策滞后。 ３、技术原因 投入和产出之间总是存在时间滞后。 ４、制度原因 契约因素：合同，定期存款 管理因素：管理层次过多，信息不灵
三、滞后变量模型
滞后变量： 是指过去时期的、对当前被解释变量产生影响的 变量。 滞后变量分为滞后解释变量与滞后被解释变量 滞后变量模型。 把滞后变量引入回归模型，这种回归模型称为滞 后变量模型。
四、滞后变量模型的分类 滞后变量模型的一般形式为
y t 0 x t 1 x t 1 k x t k 1 y t 1 2 y t 2 p y t p t
其中k、p分别为滞后解释变量和滞后被解释变量 的滞后期长度。
由上述公式生成线性组合变量Z1、Z2、Z3的数据 。然后分别估计如下经验加权模型
回归分析结果整理如下： 模型一：

计量经济学分布滞后模型

计量经济学分布滞后模型

一、数据选取某地区制造行业统计资料单位：亿元表1二、阿尔蒙法分布滞后期确定图中第一栏是y 与x 各滞后相关系数的可以看出，库存额与当年及前三年的销售额相关。

因此可以设：t t t t t u x b x b x b x b y +++++=---3322110α假定ib 可以由一个二次多项式逼近。

2.阿尔萌发估计模型直接求法 命令式T T T Z Z Z y 210545.0134.0261.19152ˆ-++-=2.方程式T T T Z Z Z y 210545.0134.0261.19152ˆ-++-=1071172.2996.0997.0115.3794.065.609.422====--F DW R R t还原后的分布滞后模型为：71.292.465.644.309.465.085.0261.15825.09152ˆ321---+++-=---tx x x x y t t t t 3.直接求模型X X(-2 ) X(-3)系数不过关。

概率不好对比上一个模型，系数检验不显著三、滞后期阿尔蒙模型调整：PDL(X,3,2)、PDL(X,4,2)、PDL(X,5,2)四期五期四期变为负的·不可取对比过后直接求的效果不如逼近好，最后选择滞后四期68.494.255.624.1122.709.49223.01917.08487.00488.17919.05.8401ˆ321---++++-=---tx x x x x y t t t t t四/阿尔蒙估计模型手工模拟过程1.做新变量Z0 ,Z1,Z2建立新序列2.回归方程115.341.244.309.4545.022.158.09152ˆ210---++-=tZ Z Z y t t t 1071,172.2,996.0,997.022====F DW R R 模型显著 3.返回原方程 设原估计方程为3322110ˆˆˆˆˆˆ---++++=t t t t x b x b x b x b y α由上一个方程有：=0ˆa0.58 =1ˆa 1.22 =2ˆa -0.545 根据almon 变换原理58.0ˆˆ00==a b265.1545.022.158.0ˆˆˆˆ2101=-+=++=a a a b 85.0ˆ4ˆ2ˆˆ2102=++=a a a b 65.0ˆ9ˆ3ˆˆ2103=++=a a a b 原模型32165.085.0265.158.09152ˆ---++++-=t t t t x x x x y五、不同权重的模型 1.建立不同权重变量Z3=x+（1/2）*x(-1)+（1/4）*x(-2)+（1/8）*x(-3)Z4=（1/4）*x+（1/2）*x(-1)+（2/3）*x(-2)+（1/4）x(-3) Z5=（1/4）*x+（1/4）*x(-1)+（1/4）*x(-2)+（1/4）*x(-3) Z6=（1/2）*x+（2/3）*x(-1)+（1/4）*x(-2)+（1/8）*x(-3) 2. 四个回归方程对比6379.178.10393ˆz y +-=302.1983453.1993.0994.053.4454.422====-F DW R R t321t 172.0345.092.0x 69.078.10393ˆ---++++-=t t t x x x y33.18302.1983453.1993.0994.022=====AIC F DW R R 通过对比选择第四个模型数据对比误差比阿尔蒙估计模型要大一些，所以最后选择阿尔蒙模型。

第九章 动态分布滞后

第九章 动态分布滞后

第九章 动态分布滞后模型在经济活动中，广泛存在着时间滞后效应，即动态性。

某些经济变量不仅受到同期各因素的影响，而且也受到过去某些时期的各种因素甚至自身的过去值的影响。

通常把这种过去时期的具有滞后作用的变量叫做滞后变量(lagged variable)，含有滞后变量的模型称为滞后变量模型。

由于其考虑了时间因素的作用，使静态分析成为动态分析，故又称为动态模型（dynamic models ）。

9.1 滞后变量模型9.1.1 滞后效应与产生滞后效应的原因一般说来被解释变量与解释变量的因果关系不一定就在瞬时发生，可能存在时间滞后，或者说解释变量的变化可能需要经过一段时间才能完全对被解释变量产生影响。

同样，被解释变量当前的变化也可能受其自身过去水平的影响，这种被解释变量受到自身或另一解释变量的前几期值影响的现象称为滞后效应，表示前几期值的变量称为滞后变量。

例如消费函数，本期消费除了受本期的收水平影响之外，还受前一期收入及前期消费水平的影响。

012131t t t t t C y y C u ββββ--=++++现实经济生活中，产生滞后效应的原因很多，主要有以下几个方面：1）经济变量自身原因。

有些变量的发展有很强的继往性，当期水平与前期水平有极为密切的关系。

例如，固定资产总量，不仅与期的固定资产投资有关，还与前期的投资有关。

2）心理原因。

由于 们固有的心理定势和行为习惯，其行为方式 往往滞后于经济形势的变化，如中彩票的人不可能很快改变其生活方式 。

因此，以往的行为延续产生的滞后效应。

3）技术原因。

在现实经济运行中，从生产到流通再到使用，每一个环节都需要一段时间，从而形成滞后期。

如当年的产在某种程度上依赖于过去若干期内投资形成的固定资产。

当年的家产吕产量主要取决于过去一年价格的高低，等待。

4）制度原因。

契约、管理制度等因素也会造成经济行为的滞后。

如定期存款到期才能提取，赞成了它对社会购买力的影响具有滞后性；过去的订货合同影响着当前产品的产量。

自回归分布滞后模型

自回归分布滞后模型

自回归分布滞后模型自回归分布滞后模型（ARIMA）是一种可用于自回归过程的统计建模技术。

它的主要优点是它能够使用时间序列数据预测未来或者检测和调整自回归过程中可能存在的性质变化。

ARIMA是一种重要的时间序列分析技术，它可以用来预测变量的自回归过程（AR），如动量（MA）和季节性过程（I）。

一、什么是自回归分布滞后模型（ARIMA）自回归分布滞后模型（ARIMA）是一种用于分析和预测时间序列数据的统计学方法。

ARIMA模型可以帮助研究者分析并预测事件的发生情况，以及由事件的发生情况产生的结果。

ARIMA模型的结构可以被定义为简单的一般线性二阶拟合模型。

二、ARIMA模型的有效性ARIMA模型通常证明是有效预测时间序列数据的一种有效方法。

无论是实现和应用于单变量和多变量时间序列上，ARIMA模型都可以为研究者提供可靠的预测结果。

在单变量的时间序列数据分析中，ARIMA 模型可以帮助研究者发现一些未知的趋势，从而判断该变量在未来的运动趋势。

三、ARIMA模型的应用ARIMA模型的应用，可以分为零度模型和非零度模型应用。

它们可以应用于单变量时间序列（零度模型）和多变量时间序列（非零度模型）上。

零度模型可以用来描述和预测单变量时间序列，而非零度模型可以用来描述和预测多变量时间序列中变量之间的关系。

此外，ARIMA模型还可以应用于时间序列平滑、广义线性模型、转换型自回归等领域。

四、ARIMA模型的优缺点ARIMA模型的优点是它能够有效地描述时间序列的差异性，可以使用时间序列数据预测未来或者检测已经发生的变化，进而找出时间序列中可能存在的自回归过程的特征，从而可以有效的预测和预测时间序列的发展趋势。

缺点是在使用自回归过程时，数据分析人员必须对变量进行较小的调整，以保持变量在ARIMA模型中是稳定的，而如果调整失败，将无法得到良好的分析结果。

第九章(滞后变量)

第九章(滞后变量)

第九章滞后变量一、滞后变量模型〔一〕滞后变量与滞后变量模型 现实经济生活中，许多经济变量不仅受同期因素的影响，而且还与某些因素，或者同自身的前期值有关。

我们通过把变量的前期值，即带有滞后作用的变量称为滞后变量，含有滞后变量的模型称为滞后变量模型。

〔二〕产生滞后效应的原因滞后效应是一个较为普遍的客观经济现象，原因可以归结为以下三个方面： 1．心理因素 2．技术因素 3．制度因素〔三〕滞后变量模型的种类 1．分布滞后模型011...t t t k x k t y x x x αβββε--=+++++2．自回归模型01122...t t t t k t k t y x y y y αββββε---=++++++〔四〕滞后变量模型的特点1．引入滞后变量能够有效地提高模型的拟合优度2．滞后变量模型是一个动态模型，可以来模拟分析经济系统的变化和调整过程存在的一些问题：〔1〕经济变量的各期值之间往往高度相关。

〔2〕降低样本的自由度，影响参数的估计精度。

〔3〕难以客观地确定滞后期的长度。

二、分布滞后模型的估计（一）经验加权法根据经验指定各期滞后变量的权数，将各期滞后变量加权组合成新的解释变量，估计变换后的模型，最后得到原模型中各参数的估计值。

〔各期权数和不一定为1〕 经常使用的权数类型有：1．递减型：各期权值是递减的。

2．常数型：各期权数值相等。

3．倒V 型：各期权数先递增后递减呈倒V 型。

历年投资对产生的影响一般为倒V 型。

？你认为经验加权法的优点和缺点在哪里 （二）阿尔蒙估计法1．原理：设有限分布滞后模型为011...t t t k t k t y x x x αβββε--=+++++根据weierstrass 定理，S.Almon 认为，连续函数2012()....()m i m f i i i i m k βαααα==++++<将这一关系代入原来的分布滞后模型，并经过适当的变量变换，可以减少模型中的变量个数，从而在消费多重共线性影响的情况下，估计模型中的参数。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

由上述公式生成线性组合变量Z1、Z2、Z3的数据 。然后分别估计如下经验加权模型
回归分析结果整理如下： 模型一：
ˆ Yt 66.60404 1.071502 Z1t ( 3.6633) R 0.994248
2
(50.9191) DW 1.440858
模型二：
F 2592
ˆ Yt = -133.1988 +1.3667 Z2t (-5.029) R = 0.989367
软件步骤： 首先，初步判断滞后期长度，命令为CROSS 在 Eviews 软件中有多项式分布滞后命令 PDL LS Y C PDL(x,k,m,d) k: 滞后期长度 m: 多项式阶数 d: 选择项。取值为 1，2，3。分别表明对多项式系 数分布的约束信息： d= 1，限制在分布的末端接近于零； d = 2，限制在分布的开头接近于零； d = 3，限制在分布的开头和末端都接近于零；
其中 0 为常数，公比
为待估参数。
通常称为分布滞后衰减率，值越接近零，衰减速 度越快。
i
0
1 2 1 4
i
按几何级数衰减的滞后结构（库伊克）
将库伊克假定式代入原模型，得
Yt 0 X t i ut
i i 0
将其滞后一期，有
Yt 1 0
i 1 i 1
X t i ut 1
两边同乘λ并与前面的公式相减，得
Yt Yt 1 ( 0 X t i ut ) ( 0 X t i ut 1 )
i i i 0 i 1


(1 ) 0 X t ( ut ut 1 )
四、滞后变量模型的分类 滞后变量模型的一般形式为
y t 0 x t 1 x t 1 k x t k 1 y t 1 2 y t 2 p y t p t
其中k、p分别为滞后解释变量和滞后被解释变量 的滞后期长度。
第九章
• 本章内容:
分布滞后模型
滞后效应与滞后变量模型 分布滞后模型的估计 自回归模型的构建
自回归模型的估计
引子:货币政策效应的时滞
货币供给的变化对经济影响很大，货币政策总是备受关注。 货币政策的影响效应存在着时间上的滞后。
在货币政策的传导过程中，货币扩张首先促使利率降低，或者一般
价格水平的上升，这需要一段时间。 这些因素对以GDP为代表的经济增长的影响，更是需要一段时间才
i 0 1i 2 i m i
2
m
t
i 0 ,1, 2 , , k ; m k
此式称为阿尔蒙多项式变换（图9.2）。
将阿尔蒙多项式变换代入分布滞后模型并整理， 模型变为如下形式
Yt 0 Z0t 1Z1t 2 Z 2t m Z mt ut
第一节 滞后效应与滞后变量模型
一、经济活动中的滞后现象
解释变量与被解释变量的因果联系不可能在短时间 内完成，在这一过程中通常都存在时间滞后，也就 是说解释变量需要通过一段时间才能完全作用于被 解释变量。 此外，由于经济活动的惯性，一个经济指标以前的 变化态势往往会延续到本期，从而形成被解释变量 的当期变化同自身过去取值水平相关的情形。 这种被解释变量受自身或其它经济变量过去值影响 的现象称为滞后效应。
2
(37.35852) DW = 1.042935
F = 1396
模型三：
ˆ Yt 121.7394 2.23973 Z 3t ( 4.8131) R 0.990077
2
(38.68578) DW 1.15853
F 1496
从上述回归分析结果可以看出，模型一的扰动项无 一阶自相关，模型二、模型三扰动项存在一阶正 自相关；再综合判断可决系数、F-检验值、t-检验 值，可以认为：最佳的方程是模型一，即权数为 （1，1/2，1/4，1/8）的分布滞后模型。
第三节 自回归模型的构建
一、库伊克模型 无限分布滞后模型中滞后项无限多，而样 本观测总是有限的，因此不可能对其直接 进行估计。要使模型估计能够顺利进行， 必须施加一些约束或假定条件，将模型的 结构作某种转化。 库伊克（Koyck）变换就是其中较具代表性 的方法。
库伊克假定：
对于如下无限分布滞后模型：
第二节 分布滞后模型的估计
一、分布滞后模型估计的困难 自由度问题；多重共线性问题；滞后长度难 于确定的问题。 处理方法： 对于有限分布滞后模型，其基本思想是设 法有目的地减少需要直接估计的模型参数 个数，以缓解多重共线性，保证自由度。 对于无限分布滞后模型，主要是通过适当 的模型变换，使其转化为只需估计有限个 参数的自回归模型。
1、分布滞后模型
被解释变量受解释变量的影响分布在解释变量不 同时期的滞后值上，即模型形如
y t 0 x t 1 x t 1 k x t k t
具有这种滞后分布结构的模型称为分布滞后模型，其 中k为滞后长度。根据滞后长度k取为有限和无限，模 型分别称为有限分布滞后模型和无限分布滞后模型。
在分布滞后模型中，各系数体现了解释变量的各个 滞后值对被解释变量的不同影响程度，即通常所说 的乘数效应： ：称为短期乘数或即期乘数，表示本期X变动 一个单位对Y值的影响大小； i ：称为延迟乘数或动态乘数()，表示过去各时 期X变动一个单位对Y值的影响大小；
：称为长期乘数或总分布乘数，表示X变动
能显示出来。
只有经过一段时间以后，支出对利率的反应增强，投资、进出口和 消费才会不断上升，货币政策才最终促使GDP增加。
通常，货币扩张对GDP影响的最高点可能是在政策实施以后的一到
两年间达到。
思考: 在现实经济活动中，滞后现象是普遍存 在的，这就要求我们在做经济分析时应该 考虑时滞的影响。 怎样才能把这类时间上滞后的经济关系 纳入计量经济模型呢？
即
Yt (1 ) 0 X t Yt 1 ( ut ut 1 )
这就是库伊克模型。上述变换过程也叫库 伊克变换。
令
(1 ) , 0 0 , 1 , ut ut ut 1
* * * *
则库伊克模型式变为
其中
z 0 t x t x t 1 x t 2 x t k z 1 t x t 1 2 x t 2 3 x t 3 kx t k z 2 t x t 1 2 x t 2 3 x t 3 k x t k
在经济运行过程中，广泛存在时间滞后效应。 某个经济变量不仅受到同期各种因素的影响，而且 也受到过去时期的各种因素甚至自身的过去值的影 响。通常把这种过去时期的，具有滞后作用的变量 叫做滞后变量 (Lagged Variable)。含有滞后变量 的模型称为滞后变量模型。 滞后变量模型考虑了时间因素的作用，使静态 分析成为动态分析，这在理论上和方法上都是一个 进步，模型也更接近于真实的经济过程。
二、产生滞后效应的原因 1、经济变量自身原因 ２、心理因素 在经济转型变革时期，人们往往由于心理定势， 而不能及时适应新的变化，表现为行为决策滞后。 ３、技术原因 投入和产出之间总是存在时间滞后。 ４、制度原因 契约因素：合同，定期存款 管理因素：管理层次过多，信息不灵
三、滞后变量模型
滞后变量： 是指过去时期的、对当前被解释变量产生影响的 变量。 滞后变量分为滞后解释变量与滞后被解释变量 滞后变量模型。 把滞后变量引入回归模型，这种回归模型称为滞 后变量模型。
记新的线性组合变量分别为：
Z1 X t 1 2 X t 1 1 X t 2 1 X t 3
4 8 1 1 2 1 Z 2 X t X t 1 X t 2 X t 3 4 2 3 4
Z3 1 4 Xt 1 4 X t 1 1 4 X t 2 1 4 X t 3
库伊克变换的缺陷：
（1）它假定无限滞后分布呈几何递减滞后结构。这种假定对某
些经济变量可能不适用，例2）库伊克模型的随机扰动项形如
ut ut ut 1
*
说明新模型的随机扰动项存在一阶自相关，且与解释变量相关 。 （3）将随机变量作为解释变量引入模型，不一定符合基本假定 。 （4）库伊克变换是纯粹的数学运算结果，缺乏经济理论依据。 这些缺陷，特别是第二个缺陷，给模型的参数估计带来定困难 。
i
s
一个单位时，由于滞后效应而形成的对Y总的影响 大小。
i 0
2、自回归模型
如果滞后变量模型的解释变量仅包括自变量X的 当期值和被解释变量的若干期滞后值，即模 型形如
y t 0 x t 2 y t 1 p y t p t
则称这类模型为自回归模型，其中p称为自回 归模型的阶数。
【例】 已知1955—1974年期间美国制造业库存 量Y和销售额X的统计资料如P267。设定有限 分布滞后模型为： 运用经验加权法，选择下列三组权数 （1）1，1/2，1/4，1/8； （2）1/4，1/2，2/3，1/4； （3）1/4，1/4，1/4，1/4； 分别估计上述模型，并从中选择最佳的方程。
Yt 0 X t 1 Yt 1 ut
* * *
*
这是一个一阶自回归模型。
库伊克变换的优点： （1）以一个滞后被解释变量代替了大量的滞 后解释变量，使模型结构得到极大简化， 最大限度地保证了自由度，解决了滞后长 度难以确定的问题； （2） 滞后一期的被解释变量与 X t 的线性相 关程度将低于X的各滞后值之间的相关程度 ，从而在很大程度上缓解了多重共线性。
二、自适应预期模型
某些经济变量的变化会或多或少地受到另一些 经济变量预期值的影响。为了处理这种经济现象 ，可以将解释变量预期值引入模型建立“期望模 型”。 例如，包含一个预期解释变量的“期望模型”可以 表现为如下形式： * y t x t 1 t