三角形全等条件SSS练习题

全等三角形的判断（SSS ）1、如图 1， AB=AD ， CB=CD ，∠ B=30 °，∠ BAD=46 °，则∠ ACD 的度数是 ()A.120 °B.125 °C.127°D.104 °2、如图 2，线段 AD 与 BC 交于点 O ，且 AC=BD ， AD=BC ， ?则下边的结论中不正确的选项是 ()A. △ ABC ≌△ BADB. ∠ CAB= ∠ DBAC.OB=OCD.∠ C=∠ D 3、在△ ABC 和△ A B C1中，已知 AB=A B，BC=B C ，则增补条件 ____________，可获得△ ABC ≌△A B C1 1 1 111．1 1 14、如图 3，AB=CD ，BF=DE ，E 、F 是 AC 上两点，且 AE=CF ．欲证∠ B= ∠ D ，可先运用等式的性质证明AF=________ ，再用“ SSS ”证明 ______≌ _______获得结论． 5、如图， AB=AC ， BD=CD ，求证：∠ 1= ∠ 2．6、如图，已知 AB=CD ，AC=BD ，求证：∠ A= ∠ D ．7、如图， AC 与 BD 交于点 O ， AD=CB ，E 、F 是 BD 上两点，且 AE=CF ，DE=BF. 请推导以下结论：⑴∠ D= ∠B ；⑵ AE ∥CF ．8、已知如图， A 、 E 、F 、 C 四点共线， BF=DE ， AB=CD.⑴请你增添一个条件，使△ DEC ≌△ BFA ；⑵在⑴的基础上，求证： DE ∥ BF.全等三角形的判断(SAS)1、如图1， AB ∥ CD ， AB=CD， BE=DF ，则图中有多少对全等三角形()A.3B.4C.5D.62、如图 2， AB=AC ，AD=AE ，欲证△ ABD ≌△ ACE ，可增补条件 ()A.∠ 1= ∠2B.∠ B= ∠ CC.∠ D= ∠ ED. ∠BAE= ∠CAD3、如图 3， AD=BC ，要获得△ ABD 和△ CDB 全等，能够增添的条件是()A.AB ∥ CDB.AD ∥ BCC.∠A= ∠ CD. ∠ABC= ∠ CDA4、如图4， AB 与 CD 交于点O， OA=OC ，OD=OB ，∠ AOD=________ ， ?依据 _________可获得△≌△ COB，进而能够获得AD=_________ ．AOD 5、如图 5，已知△ ABC 中， AB=AC ， AD 均分∠ BAC ，请增补完好过程说明△∵ AD 均分∠ BAC ，∴∠ ________=∠ _________(角均分线的定义).在△ ABD 和△ ACD 中，∵ ____________________________ ，∴△ ABD≌△ ACD（ABD）≌△ ACD的原因．6、如图 6，已知 AB=AD ， AC=AE ，∠ 1= ∠ 2，求证∠ ADE= ∠ B.7、如图，已知AB=AD ，若 AC 均分∠ BAD ，问 AC 能否均分∠ BCD ？为何？BA CD8、如图，在△ABC 和△ DEF 中， B 、 E、 F、 C，在同向来线上，下边有 4 个条件，请你在此中选 3 个作为题设，余下的一个作为结论，写一个真命题，并加以证明.①AB=DE ；② AC=DF ；③∠ ABC= ∠ DEF ；④ BE=CF.9、如图⑴， AB ⊥ BD ，DE ⊥ BD ，点 C 是 BD 上一点，且BC=DE ， CD=AB ．⑴试判断AC 与 CE 的地点关系，并说明原因．⑵如图⑵，若把△CDE 沿直线 BD 向左平移，使△CDE 的极点 C 与 B 重合，此时第⑴问中的地点关系还建立吗？(注意字母的变化)AC与BE全等三角形（三） AAS和 ASA【知识重点】1．角边角定理（ ASA）：有两角及其夹边对应相等的两个三角形全等.2 ．角角边定理（ AAS）：有两角和此中一角的对边对应相等的两个三角形全等.【典型例题】例 1．如图， AB∥ CD， AE=CF，求证： AB=CDD FC O例 2．如图，已知： AD=AE，ACD ABE ，求证：BD=CE.AE BAD E例 3．如图，已知：C D. BAC ABD ，求证：OC=OD.B CDCOAB例 4．如图已知： AB=CD，AD=BC，O是 BD中点，过 O点的直线分别交DA和 BC的延伸线于E，F. 求证： AE=CF.FDCOAB例 5．如图，已知12 3 ，AB=AD.求证：BC=DE.EA2E1OB3C D例 6．如图，已知四边形 ABCD中， AB=DC，AD=BC，点 F 在 AD 上，点 E 在 BC上， AF=CE， EF 的对角线 BD 交于 O，请问 O点有何特点？A F DOB E C【经典练习】1.△ABC和△ABC中，A A',BC BC ，C C 则△ABC与△ A BC.2．如图，点 C，F 在 BE上，12, BC EF , 请增补一个条件，使△ABC≌DFE,增补的条件是.A DB 12EC F3．在△ ABC和△A B C中，以下条件能判断△ABC和△A B C全等的个数有（）①AABB，BCBC②AA ，B B，AC AC③AABB，ACBC④AA ，B B，AB ACA ．1个 B.2 个 C.3 个 D.4 个4．如图，已知 MB=ND，MBA NDC ，以下条件不可以判断是△ABM≌△ CDN的是（）A．M NB. AB=CD M NC． AM=CND. AM∥ CN5．如图 2 所示，∠E=∠ F=90°，∠ B=∠ C， AE=AF，给出以下结论：①∠ 1=∠2② BE=CF③△ ACN≌△ ABM④ CD=DN A C B D 此中正确的结论是 __________________。

全等三角形的性质与判断（SSS、SAS、ASA 、AAS ）练习题1.如图，在△2.如图，把△则∠ A=A ABC中，∠ A=90°， D、 E 分别是 AC、 BC上的点，若△ ADB≌△ EDB≌△ EDC，则∠ C= ABC 绕点 C 顺时针旋转35°，获得△ A′ B′ C， A′ B′交 AC 于点 D，若∠ A′ DC=90°，A' BEDAD D A' C FCB'B'AB E CB CO A B1题图2题图3题图4题图3.如图，△ AOB 中，∠ B=3 0°，将△ AOB 绕点 O 顺时针旋转 52°，获得△ A′ OB′，边 A′B′与边OB交于点 C（ A′不在 OB上），则∠ A′ CO=4.如图，△ AB C≌△ ADE ， BC 的延伸线过点 E，∠ ACB= ∠ AED=10 5°，∠ CAD=1 0°，∠ B=50°，则∠ DEF=5.如图， Rt △ ABC中，∠ BAC=90°， AB=AC，分别过点 B、 C 作过点 A 的垂线 BC、CE，垂足分别为 D、E，若 BD=3 ， CE=2 ，求 DE 的长 .BCD A E6.如图， AD 是△ ABC的角均分线， DE⊥AB， DF⊥AC，垂足分别是 E、 F，连结 EF，交 AD 于 G，试判断AD与 EF的关系，并证明你的结论。

AEGFBDC7.如下图，在△ ABC 中， AD 为∠ BAC 的角均分线， DE⊥ AB 于 E， DF⊥ AC 于 F，△ ABC 的面积是28cm2,AB=20cm，AC=8cm，求 DE的长。

AE FB D C8.如图， AD=BD ， A D⊥ BC于 D， BE⊥ AC于 E， AD与 BE 订交于点 H，则 BH与 AC相等吗？为何？AEH- 1 -B D C1 / 49.已知： BD 、 CE 是△ ABC 的高，点 F 在 BD 上， BF=AC ，点 G 在 CE 的延伸线上， CG=AB ，求证： A G⊥AFG AE DFB C10.如图：在△ ABC中， BE、 CF 分别是 AC、AB 两边上的高，在 BE 上截取 BD=AC，在 CF 的延伸线上截取CG=AB，连结 AD、 AG.试判断 AD与 AG的关系怎样？并证明之.AGF EDHB C11.已知，如图：AB=AE，∠ B=∠ E，∠ BAC=∠ EAD，∠ CAF=∠ DAF，求证：AF⊥ CDAEBC F DA12.已知：∠ B=∠ E,且AB=AE。

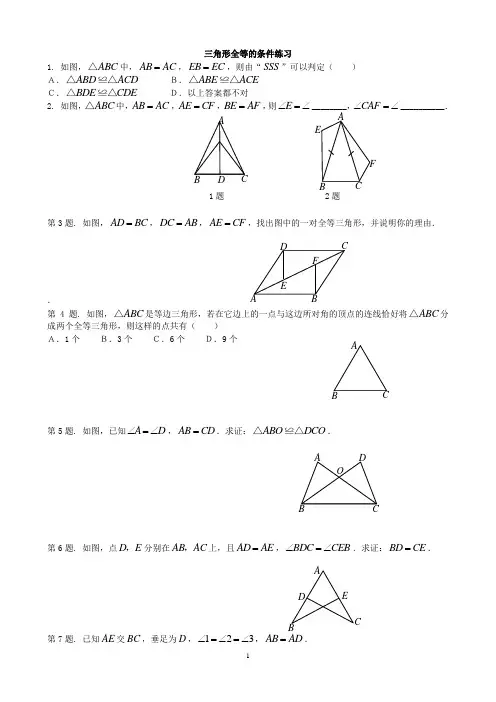
三角形全等的条件练习1. 如图，ABC △中，AB AC =，EB EC =，则由“SSS ”可以判定（ ） Ａ．ABD ACD △≌△ Ｂ．ABE ACE △≌△ Ｃ．BDE CDE △≌△ Ｄ．以上答案都不对2. 如图，ABC △中，AB AC =，AE CF =，BE AF =，则E ∠=∠________，CAF ∠=∠__________．1题 2题第3题. 如图，AD BC =，DC AB =，AE CF =，找出图中的一对全等三角形，并说明你的理由．．第4题. 如图，ABC △是等边三角形，若在它边上的一点与这边所对角的顶点的连线恰好将ABC △分成两个全等三角形，则这样的点共有（ ） Ａ．1个 Ｂ．3个 Ｃ．6个 Ｄ．9个第5题. 如图，已知A D ∠=∠，AB CD =．求证：ABO DCO △≌△．第6题. 如图，点D E ，分别在AB AC ，上，且AD AE =，BDC CEB ∠=∠．求证：BD CE =．AB D CA E FC BA C F D EB AB C A D O BC ADE BC求证：（1）ADC ABE ∠=∠；（2）DC BE =．第8题. 如图，已知ABC △为等边三角形，QR AB ⊥，垂足为R ，PQ AC ⊥，垂足为Q ，RP BC ⊥，垂足为P ，且AR BP CQ ==．求证：RPQ △为等边三角形．第9题. 如图，已知点A C ，在EF 上，AD BC =，AD BC ∥，DE BF ∥．求证：DE BF =．第10题. 如图，在ABC △和DEF △中，已知AB DE =，BC EF =，根据（SAS ）判定ABC DEF △≌△，还需的条件是（ ） Ａ．A D ∠=∠ Ｂ．B E ∠=∠ Ｃ．C F ∠=∠Ｄ．以上三个均可以A BED C1 23 4ARB PC QF CD E A B A D B C E FＡ．两边一夹角 Ｂ．两角一夹边 Ｃ．三边 Ｄ．三角 第12题. 如图，已知AB BD ⊥，垂足为B ，ED BD ⊥，垂足为D ，AB CD =，BC DE =，则A C E ∠＝___________．第13题. 如图，已知AB AC =，AD AE =，BAC DAE ∠=∠．求证：BD CE =．第14题. 下列各命题中，真命题是（ ）Ａ．如果两个三角形面积不相等，那么这两个三角形不可能全等 Ｂ．如果两个三角形不全等，那么这两个三角形面积一定不相等Ｃ．如果MNP EFG △≌△，M N P E F G ''''''△≌△，那么MNP △与EFG △的面积的和等于M N P '''△与E F G '''△面积的和Ｄ．如果MNP EFG △≌△，M N P E F G ''''''△≌△，那么MNP M N P EFG E F G ''''''△+△≌△+△ 第15题. 如图，已知AF BE =，A B ∠=∠，AC BD =．求证：F E ∠=∠．第16题. 如图，点P 是AOB ∠的平分线上的一点，作PD OA ⊥，垂足为D ，PE OB ⊥垂足为E ，DE 交OC 于点F ．（1）你能找到几对全等三角形？请说明理由；（2）你能确定图中共有几个直角吗？请说明理由．AE C B D A E DB C CD A BEF O E B A CD F P的延长线于F ．求证：OE OF =．第18题. 如图，已知AB CD =，AE DF =，CE BF =．求证：AF DE =．第19题. 对于下列各组条件，不能判定ABC A B C '''△≌△的一组是（ ） Ａ．A A '∠=∠，B B '∠=∠，AB A B ''= Ｂ．A A '∠=∠，AB A B ''=，AC A C ''= Ｃ．A A '∠=∠，AB A B ''=，BC B C ''= Ｄ．AB A B ''=，AC A C ''=，BC B C ''=第21题. 如图，已知在ABC △和A B C '''△中，AM 与A M ''分别是BC B C ''，上的中线，AB A B ''=，AC A C ''=，AM A M ''=．求证：ABC A B C '''△≌△． ．第22题. 如图，已知在ABC △中，AB AC =，12∠=∠．求证：AD BC ⊥，BD DC =．A BF E C DA B M C A ' B ' M ' C ' A B C D 21 3 4B '，使OB BO '=，延长CO 到C '，使OC CO '=，得到A B C '''△，A B C '''△与ABC △是否全等？这两个三角形的对应边是否平行？为什么？第24题. 如图，在ABC △中，90C ∠=，D E ，分别为AC AB ，上的点，且AD BD =，AE BC =，DE DC =．求证：DE AB ⊥．第25题. 如图，AB AC =，要使△ABE ≌△ACD ，应添加的条件是 ，（添加一个条件即可）第26题. 如图，四边形ABCD 中，AC 垂直平分BD ，垂足为点O ． （1）图中有多少对全等三角形？请把它们都写出来；（2）任选（1）中的一对全等三角形加以证明．OABCC 'A 'B 'EADBC AD B OECA B D C O件（ ）A ．AB ED = B ．AB FD =C ．AC FD = D ．A F ∠=∠第28题. 小明用四根竹棒扎成如图所示的风筝框架，已知AB CD =，AD CB =，你认为小明的风筝两脚大小相同吗（即B ∠，D ∠相等吗）？请说明理由．第29题. 小民用五根木条钉成了如图所示的两个三角形，且AB AC =，BD CD =，若ABD △为锐角三角形，则ACD △中的最大角α的取范围是（ ）Ａ．3060<α≤ Ｂ．4560<α≤ Ｃ．4590<α≤Ｄ．6090<α≤第30题. 已知：ABC △的三边分别为a b c ，，，A B C '''△的三边分别为a b c '''，，，且有222222222a a b b c c a b b c ca ''''''+++++=++，则ABC △与A B C '''△（ ） Ａ．一定全等 Ｂ．不一定全等 Ｃ．一定不全等 Ｄ．无法确定第31题. 如图，已知12∠=∠，34∠=∠．求证：BE CD =．第32题. 你见过形如图所示的风筝吗？开始制作时，AB CD =，AC DB =，后来为了加固，又过点O 加了一根竹棒EF ，分别交AB CD ，于点E F ，，且AOE DOF ∠=∠，你认为OE OF ，相等吗？请说明理由．A B DCO AC D B AB CDA1 2 3 4 D E B CA D F E OB C．第34题. 如图，已知12∠=∠，ABC DCB ∠=∠，AC DB =．求证：ABC DCB △≌△． ．第35题. 在ABC △和A B C ''△中，①AB A B ''=；②BC B C ''=；③AC A C ''=；④A A '∠=∠；⑤B B '∠=∠则下列条件中不能保证ABC A B C '''△≌△的是（ ） Ａ．①②③ Ｂ．①②⑤ Ｃ．②④⑤ Ｄ．①③⑤第37题. 如图，AB AC BE =，与CF 交于点O ，EC FB 与相等吗？为什么？第38题. 如图，AB DC AB DC AC BD =∥，，与相交于点O ，你能找出两对全等的三角形吗？你能说明其中的道理吗？AB OCD 2 A D C B 1 ABCDO第39题. 已知：如图，D 是△ABC 的边AB 上一点，AB FC ∥，DF AC E 交于点，DE FE =．AE CE =求证:．第40题. 如图，给出五个等量关系：①AD BC =、②AC BD =、③CE DE =、④D C ∠=∠、⑤DAB CBA ∠=∠．请你以其中两个为条件，另三个中的一个为结论，推出一个正确的命题（只需写出一种情况），并加以证明． 已知：求证：证明：第41题. 如图，A B ，两点分别位于池塘两端，小明和同伴用下面的方法测量AB 间的距离：先在地上取一个可以直接到达A 点和B 点的点C ，连接AC 并延长到D ，使CD AC =，连接BC 并延长到E ，使CE BC =，连接DE ，那么量出DE 的长，就是A B ，的距离，小明和同伴的测量方法对不对？为什么？第42题. 如图，要测量河两岸相对的两点A ，B 的距离，可以在AB 的垂线BF 上取两点C D ，，使CD BC =，再定出BF 的垂线DE ，使A C E ，，在一条直线上，这时测得的DE 的长就是AB 的长，为什么？ AD B C FEA B C E DA B C E D C D F E A B第43题. 如图A B ，两个建筑分别位于河的两岸，要测得它们之间的距离，可以从B 出发沿河岸画一条射线BF ，在BF 上截取BC CD =，过D 作DE AB ∥，使E C A ，，在同一条直线上，则DE 的长就是A B ，之间的距离．请你说明道理．你还能想出其他方法吗？第44题. 如图，已知90B D ∠=∠=，AB AD =．求证：BC DC =．．第45题. 如图，已知AD AF ，分别是两个钝角ABC △和ABE △的高，如果AD AF =，AC AE =． 求证：BC BE =．第46题. 使两个直角三角形全等的条件是（ ） Ａ．一个锐角对应相等 Ｂ．两个锐角对应相等 Ｃ．一条边对应相等 Ｄ．两条直角边对应相等第47题. 如图，有一正方形窗架，盖房时为了稳定，在上面钉了两个等长的木条GF 与GE E F ，，分别是AD BC ，的中点，G 是AB 的中点吗？AB C F E D A CD B A D C BE F A B CF E D G第48题. 如图，已知A F E B ，，，四点共线，AC CE ⊥，BD DF ⊥，AE BF =，AC BD =． 求证：ACF BDE △≌△．第49题. 判定两个直角三角形全等的方法有 Ａ．两条直角边对应相等 Ｂ．斜边和一锐角对应相等 Ｃ．斜边和一条直角边对应相等 Ｃ．两个面积相等其中不正确的为（ ）第50题. 将一张矩形纸片沿对角线剪开，得到两张三角形纸片，再将这两张三角形纸片摆放成如下右图的形式，使点B ，F ，C ，D 在同一条直线上． （1）求证：AB ED ⊥；（2）若PB BC =，请找出图中与此条件有关的一对．．全等三角形，并给予证明．A F DE BC AEPM BF CDNACBD FE。

全等三角形的判定（SSS）1、如图1，AB=AD，CB=CD，∠B=30°，∠BAD=46°，则∠ACD的度数是( )°°°°2、如图2，线段AD与BC交于点O，且AC=BD，AD=BC，•则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBA =OC D.∠C=∠D3、在△ABC和△A1B1C1中，已知AB=A1B1，BC=B1C1，则补充条件____________，可得到△ABC≌△A1B1C1．4、如图3，AB=CD，BF=DE，E、F是AC上两点，且AE=CF．欲证∠B=∠D，可先运用等式的性质证明AF=________，再用“SSS”证明______≌_______得到结论．5、如图，AB=AC，BD=CD，求证：∠1=∠2．6、如图，已知AB=CD，AC=BD，求证：∠A=∠D．7、如图，AC与BD交于点O，AD=CB，E、F是BD上两点，且AE=CF，DE=BF.请推导下列结论：⑴∠D=∠B；⑵AE∥CF．8、已知如图，A、E、F、C四点共线，BF=DE，AB=CD.⑴请你添加一个条件，使△DEC≌△BFA；⑵在⑴的基础上，求证：DE∥BF.全等三角形的判定方法SAS专题练习1.如图，AB=AC，AD=AE，欲证△ABD≌△ACE，可补充条件( )A.∠1=∠2B.∠B=∠CC.∠D=∠ED.∠BAE=∠CAD2.能判定△ABC≌△A′B′C′的条件是（）A．AB=A′B′，AC=A′C′，∠C=∠C′B. AB=A′B′，∠A=∠A′，BC=B′C′C. AC=A′C′，∠A=∠A′，BC=B′CD. AC=A′C′，∠C=∠C′，BC=B′C3.如图，AB与CD交于点O，OA=OC，OD=OB，∠AOD= ，根据_________可得到△AOD≌△COB，从而可以得到AD=_________．4.如图，已知BD=CD，要根据“SAS”判定△ABD≌△ACD，则还需添加的条件是。

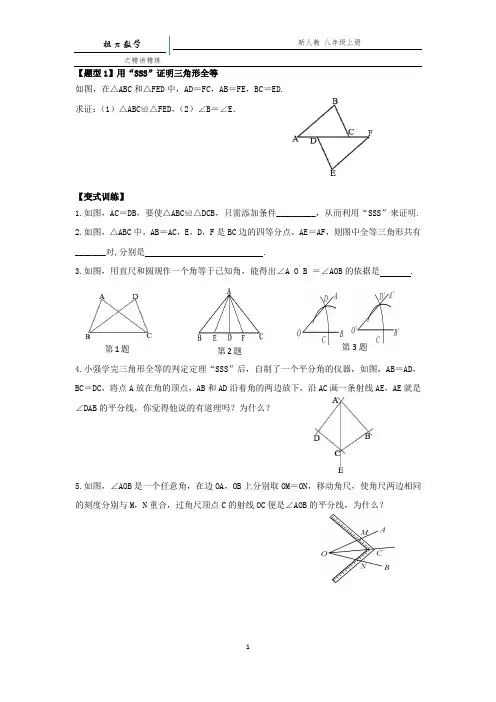
【题型1】用“SSS ”证明三角形全等
如图，在△ABC 和△FED 中，AD ＝FC ，AB ＝FE ，BC ＝ED.
求证：（1）△ABC ≌△FED ，（2）∠B ＝∠E ．
【变式训练】
1.如图，AC ＝DB ，要使△ABC ≌△DCB ，只需添加条件_________，从而利用“SSS”来证明.
2.如图，△ABC 中，AB ＝AC ，E ，D ，F 是BC 边的四等分点，AE ＝AF ，则图中全等三角形共有_______对,分别是 .
3.如图，用直尺和圆规作一个角等于已知角，能得出∠A ′O ′B ′
＝∠AOB 的依据是 .
4.
小强学完三角形全等的判定定理“SSS”后，自制了一个平分角的仪器，如图，AB ＝AD ，BC ＝DC ，将点A 放在角的顶点，AB 和AD 沿着角的两边放下，沿AC 画一条射线AE ，AE 就是∠DAB 的平分线，你觉得他说的有道理吗？为什么？
5.如图，∠AOB 是一个任意角，在边OA ，OB 上分别取OM ＝ON ，移动角尺，使角尺两边相同的刻度分别与M ，N 重合，过角尺顶点C 的射线OC 便是∠AOB 的平分线，为什么？
第1题 第3题 第2题
6.如图，A，C，F，D四点在同一直线上，AB＝DE，BC＝EF，AF＝DC.求证：AB∥DE.
7.如图，AB＝AC，AD＝AE，BE＝CD.求证：∠B＝∠C，∠DAB＝∠EAC．
8.如图，AB＝CD，AD＝CB.求证：(1)∠BAD＋∠ADC＝180°；（2）∠B＝∠D.
9.如图，AB＝DC，AC＝DB.求证：∠1＝∠2．
10.如图，AB＝AC，AD＝AE，BD＝CE.求证：∠3＝∠1＋∠2.。

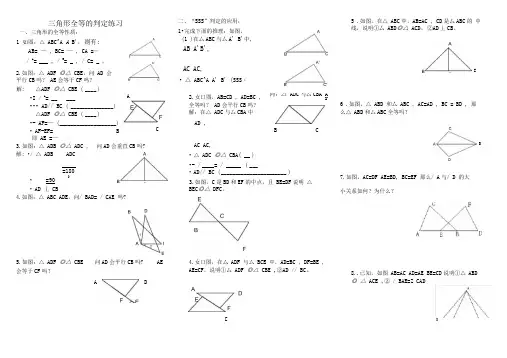
三角形全等的判定练习一、三角形的全等性质：1 如图：△ ABC^A A B'，则有:AB= —, BC= —, CA =—/ A= ___ , / B= _ , / C= _ ,二、“SSS”判定的应用：1•完成下面的推理：如图，(1 )在厶ABC与厶A' B'中,AB A'B',2.如图：△ ADF ◎△ CBE，问AD 会平行CB吗？AE会等于CF吗？AC AC,• △ ABC^A A' B' (SSS・5 .如图，在△ ABC中，AB=AC , CD是厶ABC的中线，说明①厶ABD◎△ ACD。

②AD丄CB。

C 解: △A DF ◎△ CBE ( ____ )•I / A= __ (___••• AD// BC ( _______________ )△A DF ◎△ CBE ( ____ )•- AF=—( ____________________ )• AF-EF= B CA 2.女口图，AB=CD , AD=BC ,全等吗？AD会平行CB吗？解：在△ ADC与厶CBA中AD ,问：△ ADC与厶CBA ArB C6 .如图，△ ABD 和厶ABC , AC=AD , BC = BD , 那么△ ABD和厶ABC全等吗？即AE =—3.如图：△ ADB ◎△ ADC ,解: •/ △ ADB ADCAC AC,•=90•AD 丄CB=180问AD会垂直CB吗?4.如图：△ ABC ADE，问/ BAD= / CAE 吗?5.如图：△ ADF ◎△ CBE会等于CF吗？AE问AD会平行CB吗?A D•△ ADC ◎△ CBA( __ )•- / ____ = / _____ ( ___•AD// BC ( _______________________ )3.如图，C是BD和EF的中点，且BE=DF说明△BEC◎△ DFC。

4.女口图，在厶ADF 与厶BCE 中，AD=BC , DF=BE ,AE=CF，说明①厶ADF ◎△ CBE ,②AD // BC。

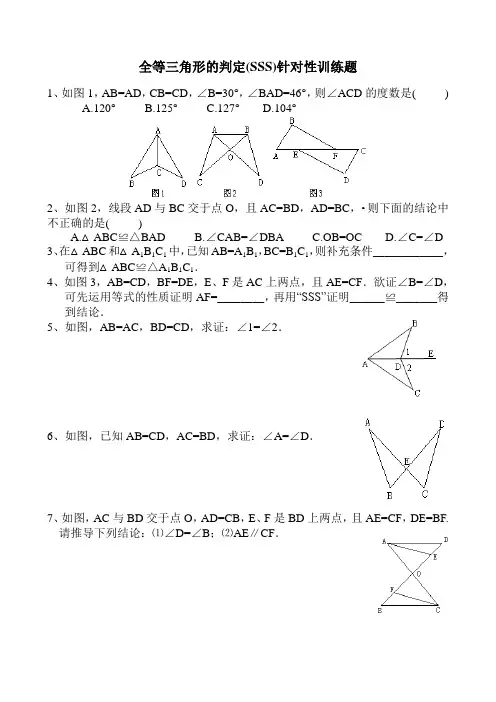
全等三角形的判定(SSS)针对性训练题1、如图1，AB=AD，CB=CD，∠B=30°，∠BAD=46°，则∠ACD的度数是( )A.120°B.125°C.127°D.104°2、如图2，线段AD与BC交于点O，且AC=BD，AD=BC，•则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D3、在△ABC和△A1B1C1中，已知AB=A1B1，BC=B1C1，则补充条件____________，可得到△ABC≌△A1B1C1．4、如图3，AB=CD，BF=DE，E、F是AC上两点，且AE=CF．欲证∠B=∠D，可先运用等式的性质证明AF=________，再用“SSS”证明______≌_______得到结论．5、如图，AB=AC，BD=CD，求证：∠1=∠2．6、如图，已知AB=CD，AC=BD，求证：∠A=∠D．7、如图，AC与BD交于点O，AD=CB，E、F是BD上两点，且AE=CF，DE=BF.请推导下列结论：⑴∠D=∠B；⑵AE∥CF．8、已知如图，A、E、F、C四点共线，BF=DE，AB=CD.⑴请你添加一个条件，使△DEC≌△BFA；⑵在⑴的基础上，求证：DE∥BF.全等三角形的判定(SAS)针对性训练题1、如图1，AB∥CD，AB=CD，BE=DF，则图中有多少对全等三角形( )A.3B.4C.5D.62、如图2，AB=AC，AD=AE，欲证△ABD≌△ACE，可补充条件( )A.∠1=∠2B.∠B=∠CC.∠D=∠ED.∠BAE=∠CAD3、如图3，AD=BC，要得到△ABD和△CDB全等，可以添加的条件是( )A.AB∥CDB.AD∥BCC.∠A=∠CD.∠ABC=∠CDA4、如图4，AB与CD交于点O，OA=OC，OD=OB，∠AOD=________，•根据_________可得到△AOD≌△COB，从而可以得到AD=_________．5、如图5，已知△ABC中，AB=AC，AD平分∠BAC，请补充完整过程说明△ABD≌△ACD的理由．∵AD平分∠BAC，∴∠________=∠_________(角平分线的定义).在△ABD和△ACD中，∵____________________________，∴△ABD≌△ACD（）DC BA 6、如图6，已知AB=AD ，AC=AE ，∠1=∠2，求证∠ADE=∠B.7、如图，已知AB=AD ，若AC 平分∠BAD ，问AC 是否平分∠BCD ？为什么？8、如图，在△ABC 和△DEF 中，B 、E 、F 、C ，在同一直线上，下面有4个条件，请你在其中选3个作为题设，余下的一个作为结论，写一个真命题，并加以证明.①AB=DE ； ②AC=DF ； ③∠ABC=∠DEF ； ④BE=CF.9、如图⑴，AB ⊥BD ，DE ⊥BD ，点C 是BD 上一点，且BC=DE ，CD=AB ．⑴试判断AC 与CE 的位置关系，并说明理由． ⑵如图⑵，若把△CDE 沿直线BD 向左平移，使△CDE 的顶点C 与B 重合，此时第⑴问中AC 与BE 的位置关系还成立吗？(注意字母的变化)全等三角形的判定(AAS)和(ASA)针对性训练题 【典型例题】例1．如图，AB ∥CD ，AE=CF ，求证：AB=CD例2．如图，已知：AD=AE ，ABE ACD ∠=∠，求证：BD=CE.例3．如图，已知：ABD BAC D C ∠=∠∠=∠.，求证：OC=OD.例4．如图已知：AB=CD ，AD=BC ，O 是BD 中点，过O 点的直线分别交DA和BC 的延长线于E ，F.求证：AE=CF. 例5．如图，已知321∠=∠=∠，AB=AD.求证：BC=DE.例6．如图，已知四边形ABCD 中，AB=DC ，AD=BC ，点F 在AD 上，点E 在BC 上，AF=CE ，EF 的对角线BD 交于O ，请问O 点有何特征？AEABDC EO12 3 AFDOBECABCDO【经典练习】1.△ABC 和△C B A '''中，C B C B A A ''='∠=∠,'，C C '∠=∠则△ABC 与△C B A ''' .2．如图，点C ，F 在BE 上，,,21EF BC =∠=∠请补充一个条件，使△ABC ≌DFE,补充的条件是 .3．在△ABC 和△C B A '''中，下列条件能判断△ABC 和△C B A '''全等的个数有（ ） ①A A '∠=∠ B B '∠=∠，C B BC ''= ②A A '∠=∠，B B '∠=∠，C A C A ''=' ③A A '∠=∠ B B '∠=∠，C B AC ''= ④A A '∠=∠，B B '∠=∠，C A B A ''='A ． 1个B. 2个C. 3个D. 4个4．如图，已知MB=ND ，NDC MBA ∠=∠，下列条件不能判定是△ABM ≌△CDN 的是（ ）A ．N M ∠=∠ B. AB=CDC ． AM=CND. AM ∥CN5．如图所示， ∠E =∠F =90°，∠B =∠C ，AE =AF ， 给出下列结论①∠1=∠2 ②BE=CF ③△ACN ≌△ABM④CD=DN ，其中正确的结论是_________。

全等三角形的判定（SSS）1、如图1，AB=AD，CB=CD，∠B=30°，∠BAD=46°，则∠ACD的度数是( )A.120°B.125°C.127°D.104°2、如图2，线段AD与BC交于点O，且AC=BD，AD=BC，•则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D3、在△ABC和△A1B1C1中，已知AB=A1B1，BC=B1C1，则补充条件____________，可得到△ABC≌△A1B1C1．4、如图3，AB=CD，BF=DE，E、F是AC上两点，且AE=CF．欲证∠B=∠D，可先运用等式的性质证明AF=________，再用“SSS”证明______≌_______得到结论．5、如图，已知AB=CD，AC=BD，求证：∠A=∠D．6、如图，AC与BD交于点O，AD=CB，E、F是BD上两点，且AE=CF，DE=BF.请推导下列结论：⑴∠D=∠B；⑵AE∥CF．7、已知如图，A、E、F、C四点共线，BF=DE，AB=CD.⑴请你添加一个条件，使△DEC≌△BFA；⑵在⑴的基础上，求证：DE∥BF.全等三角形的判定(SAS)1、如图1，AB∥CD，AB=CD，BE=DF，则图中有多少对全等三角形( )A.3B.4C.5D.62、如图2，AB=AC，AD=AE，欲证△ABD≌△ACE，可补充条件( )D CBA A.∠1=∠2 B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD3、如图3，AD=BC ，要得到△ABD 和△CDB 全等，可以添加的条件是( ) A.AB ∥CD B.AD ∥BC C.∠A=∠C D.∠ABC=∠CDA4、如图4，AB 与CD 交于点O ，OA=OC ，OD=OB ，∠AOD=________，•根据_________可得到△AOD ≌△COB ，从而可以得到AD=_________．5、如图5，已知△ABC 中，AB=AC ，AD 平分∠BAC ，请补充完整过程说明△ABD ≌△ACD 的理由． ∵AD 平分∠BAC ， ∴∠________=∠_________(角平分线的定义). 在△ABD 和△ACD 中，∵____________________________， ∴△ABD ≌△ACD （ ） 6、如图6，已知AB=AD ，AC=AE ，∠1=∠2，求证∠ADE=∠B.7、如图，已知AB=AD ，若AC 平分∠BAD ，问AC 是否平分∠BCD ？为什么？8、如图，在△ABC 和△DEF 中，B 、E 、F 、C ，在同一直线上，下面有4个条件，请你在其中选3个作为题设，余下的一个作为结论，写一个真命题，并加以证明. ①AB=DE ； ②AC=DF ； ③∠ABC=∠DEF ； ④BE=CF.9、如图⑴，AB ⊥BD ，DE ⊥BD ，点C 是BD 上一点，且BC=DE ，CD=AB ．⑴试判断AC 与CE 的位置关系，并说明理由．⑵如图⑵，若把△CDE 沿直线BD 向左平移，使△CDE 的顶点C 与B 重合，此时第⑴问中AC 与BE 的位置关系还成立吗？(注意字母的变化)全等三角形（三）AAS 和ASA【知识要点】1．角边角定理（ASA ）：有两角及其夹边对应相等的两个三角形全等.2．角角边定理（AAS ）：有两角和其中一角的对边对应相等的两个三角形全等.【典型例题】例1．如图，AB ∥CD ，AE=CF ，求证：AB=CD例2．如图，已知：AD=AE ，ABE ACD ∠=∠，求证：BD=CE.例3．如图，已知：ABD BAC D C ∠=∠∠=∠.，求证：OC=OD. 例4．如图已知：AB=CD ，AD=BC ，O 是BD 中点，过O 点的直线分别交DA 和BC 的延长线于E ，F.求证：AE=CF.例5．如图，已知321∠=∠=∠，AB=AD.求证：BC=DE.例6．如图，已知四边形ABCD 中，AB=DC ，AD=BC ，点F 在AD 上，点E 在BC 上，AF=CE ，EF 的对角线BD 交于O ，请问O 点有何特征？AABD C EO12 3AFDOBEC【经典练习】1.△ABC 和△C B A '''中，C B C B A A ''='∠=∠,'，C C '∠=∠则△ABC 与△C B A ''' .2．如图，点C ，F 在BE 上，,,21EF BC =∠=∠请补充一个条件，使△ABC ≌DFE,补充的条件是 .3．在△ABC 和△C B A '''中，下列条件能判断△ABC 和△C B A '''全等的个数有（ ） ①A A '∠=∠ B B '∠=∠，C B BC ''= ②A A '∠=∠，B B '∠=∠，C A C A ''=' ③A A '∠=∠ B B '∠=∠，C B AC ''= ④A A '∠=∠，B B '∠=∠，C A B A ''=' A ． 1个 B. 2个 C. 3个 D. 4个4．如图，已知MB=ND ，NDC MBA ∠=∠，下列条件不能判定是△ABM ≌△CDN 的是（ ）A ． N M ∠=∠ B. AB=CD C ． AM=CN D. AM ∥CN 5．如图2所示， ∠E =∠F =90°，∠B =∠C ，AE =AF ，给出下列结论：①∠1=∠2 ②BE=CF ③△ACN ≌△ABM ④CD=DN其中正确的结论是_________ _________。

全等三角形：1、能够‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗的两个图形叫全等形。

2、能够‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗的两个三角形叫全等三角形，重合的‗‗‗叫对应顶点，重合的边叫‗‗‗‗‗‗‗‗，重合的角叫‗‗‗‗‗‗‗‗。

3、全等三角形的‗‗‗‗‗‗‗‗相等，对应角‗‗‗‗‗‗‗‗。

4、经过平移、翻折、旋转后的图形与原图形‗‗‗‗‗‗‗。

5、如图所示，△ABC与△DEF全等，可记作△ABC‗‗‗‗‗△DEF，其中点A与点‗‗‗‗‗是对应顶点，∠B与‗‗‗‗‗是对应角，AC与‗‗‗‗‗是对应边。

6、如图，已知△ABD≌△ECF，则相等的边有‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗；相等的角有‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗。

7、已知△ABC≌△EDF，则对应边为‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗，对应角为‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗。

8、已知：如图，△ABD与△CDB全等，∠ABD=∠CDB，写出其对应边和对应角。

9、如图所示，△ABC≌△DEF，若AB=DE，∠B=50°，∠C=70°，∠E=50°，AC=2cm，求∠D的度数及DF的长。

10、如图，△AEC≌△ADB，点E和点D是对应顶点。

（1）写出它们的对应边和对应角；（2）若∠A=50°，∠ABD=39°，且∠1=∠2，求∠1的度数。

11、如图，△ABC≌△ADE，∠DAC=60°，∠BAE=100°，BC、DF相交于点F，求∠DFB的度数。

12、如图所示，A，D，E三点在同一直线上，且△BAD≌△ACE。

试说明：（1）BD=DE+CE；（2）△ABD满足什么条件时，BD∥CE？1、三边分别‗‗‗‗的两个三角形全等，可以简写成‗‗‗‗‗‗‗或‗‗‗‗‗‗‗。

专题12.4全等三角形的判定（SSS 与SAS）（精选精练）（专项练习）一、单选题（本大题共10小题，每小题3分，共30分）1．（23-24八年级上·河南信阳·期末）如图，AB AC =，BD CD =，35BAD ∠=︒，120ADB ∠=︒，则C ∠的度数为（）A ．25︒B ．30︒C ．35︒D ．55︒2．（23-24八年级上·广西百色·期末）如图，O 为AC 的中点，若要利用“SAS ”来判定△≌△AOB COD ，则应补充的一个条件是（）A ．A C ∠=∠B ．AB CD =C ．B C ∠=∠D ．OB OD=3．（22-23九年级上·重庆大渡口·期末）如图，在正方形ABCD 中，点E F ，分别在边CD BC ，上，且DE CF =，连接AE DF ，，DG 平分ADF ∠交AB 于点G ．若70AED ∠=︒，则AGD ∠的度数为（）A ．50︒B ．55︒C ．60︒D ．65︒4．（2024·陕西咸阳·三模）如图，在ABC 中，D 为边BC 的中点，1AB =，2AD =，延长AD 至点E ，使得DE AD =，则AC 长度可以是（）A ．4B ．5C ．6D ．75．（17-18八年级上·辽宁营口·阶段练习）如图，AD 是ABC 的中线，E ，F 分别是AD 和AD 延长线上的点，且DE DF =，连接BF CE ，．则下列说法：①CE BF =；②ABD △和ACD 面积相等；③BF CE ∥；④BDF CDE △△≌．其中正确的有（）A ．4个B ．3个C ．2个D ．1个6．（23-24八年级上·安徽安庆·期末）如图，已知方格纸中是4个相同的正方形，则1∠与2∠的和为（）A ．80︒B ．90︒C ．100︒D ．110︒7．（23-24八年级上·湖北孝感·期中）如图，已知48AOB ∠=︒，点C 为射线OB 上一点，用尺规按如下步骤作图：①以点O 为圆心，以任意长为半径作弧，交OA 于点D ，交OB 于点E ；②以点C 为圆心，以OD 长为半径作弧，交OC 于点F ；③以点F 为圆心，以DE 长为半径作弧，交前面的弧于点G ；④连接CG 并延长交OA 于点H ．则AHC ∠的度数为（）A ．24︒B ．42︒C ．48︒D ．96︒8．（23-24八年级上·山东德州·阶段练习）如图，平面上有ACD 与BCE ，其中AD 与BE 相交于P 点，如图，若AC BC AD BECD CE ===，，，55ACE ∠=︒，155BCD ∠=︒，则BPD ∠的度数为（）A ．110︒B ．125︒C ．130︒D ．155︒9．（23-24七年级下·山西太原·阶段练习）如图1，两个大小不同的三角板叠放在一起，图2是由它得到的抽象几何图形，已知AB AC =，AE AD =，90CAB DAE ∠=∠=︒，且点B ，C ，E 在同一条直线上，10cm BC =，4cm CE =，连接DC ．现有一只壁虎以2cm/s 的速度沿B C D --的路线爬行，则壁虎爬到点D 所用的时间为（）A ．10sB ．11sC ．12sD ．13s10．（21-22八年级上·云南昭通·期末）如图，AD 是ABC 的中线，E ，F 分别是AD 和AD 延长线上的点，且CE BF ，连接BF CE ，，下列说法：①DE DF =；②ABD 和ACD 面积相等；③CE BF =；④BDF CDE ≌；⑤CEF F ∠∠=．其中正确的有（）A ．1个B ．5个C ．3个D ．4个二、填空题（本大题共8小题，每小题4分，共32分）11．（23-24八年级上·江苏南京·期末）如图，已知12∠=∠，要用“SAS ”判定ABD ACD △≌△，则需要补充的一个条件为．12．（23-24八年级上·河北保定·期末）如图，在ABC 与ADE V 中，E 在BC 边上，AD AB =，AE AC =，DE BC =，若125∠=︒，则DAB ∠=．13．（23-24八年级上·吉林松原·期中）如图，为了测量A 、B 两点之间的距离，在地面上找到一点C ，使90ACB ∠=︒，然后在BC 的延长线上确定点D ，使BC CD =，那么只要测量出AD 的长度就得到A 、B 两点之间的距离，其中ABC ADC △△≌的依据是．14．（23-24八年级上·重庆江津·期中）如图，BE BA =，DE AB ∥，DE BC =，若3825BAC E ∠=︒∠=︒，，则BDE ∠=．15．（23-24八年级上·江苏泰州·期中）如图，在ABC 中，点D 、E 分别在AC 、BC 上，AD DE =，AB BE =，80A ∠=︒，则DEC ∠=︒．16．（23-24八年级上·河南洛阳·期中）如图，在长方形ABCD 中，20cm AB =，点E 在边AD 上，且12cm AE =．动点P 在边AB 上，从点A 出发以4cm/s 的速度向点B 运动，同时，点Q 在边BC 上，以cm/s v 的速度由点B 向点C 运动，若在运动过程中存在EAP 与PBQ 全等的时刻，则v 的值为．17．（23-24八年级上·山东菏泽·阶段练习）已知，如图，在ABC 中，点D 是AB 上一点，CD 平分ACB ∠，2A ADC ∠=∠，6BD =，4AC =，则BC 的长为．18．（23-24九年级下·江苏泰州·阶段练习）如图，AC 平分DCB ∠，CB CD =，DA 的延长线交BC 于点E ，若BAE x ∠=︒，则EAC ∠的度数为．（用含x 的代数式表示）．三、解答题（本大题共6小题，共58分）19．（8分）（23-24八年级上·陕西商洛·阶段练习）如图，在ABF △和DCE △中，,,AB DC AF DE BE CF ===，且点,,,B E F C 在同一条直线上．求证：B C ∠=∠．20．（8分）（23-24八年级上·江苏泰州·期中）如图，点B F C E 、、、在一条直线上，AB DE =，,,AC DF BF CE AD ==交BE 于点O ．（1）求证：B E ∠=∠；（2）求证：,AD BE 互相平分．21．（10分）（23-24八年级上·天津宁河·期中）如图，已知AD AB AC AE DAB CAE ==∠=∠，，，连接DC BE ，．（1）求证：BAE DAC ≌；（2）若13520CAD D ∠=︒∠=︒，，求E ∠的度数．22．（10分）（23-24七年级下·陕西西安·阶段练习）如图，在ABC 中，D 为AB 上一点，E 为AC 中点，连接DE 并延长至点F 使得EF ED =，连CF ．（1）求证：CF AB ∥；（2）若50ABC ∠=︒，连接BE ，CA 平分BCF ∠，求A ∠的度数．23．（10分）（23-24七年级下·陕西西安·阶段练习）已知等腰三角形ABC ，AB AC =，D 为射线BC 上一动点，连接AD ，以AD 为边在直线AD 的右侧作等腰三角形ADE ，DAE BAC ∠=∠，AD AE =，连接CE ．（1）如图1，当点D 在边BC 上时，请探究BC ，CD ，CE 之间的数量关系．（2）如图2，当点D 在BC 的延长线上时，（1）中BC ，CD ，CE 之间的数量关系是否仍然成立？若成立，请说明理由；若不成立，请你写出新的结论，并说明理由．24．（12分）（23-24七年级下·陕西咸阳·阶段练习）如图，在ABC 中，AD 是BC 边上的中线，分别以AB ，AC 为直角边作直角ABE 和ACF △，其中AB AE =，90BAE ∠=︒，AC AF =，90CAF =︒∠，连接EF ，延长AD 至点G ，使DG AD =，连接BG ．【初步探索】（1）试说明：AC BG ∥；【衍生拓展】（2）探究EF 和AD 之间的数量关系，并说明理由．参考答案：1．A【分析】本题主要考查了全等三角形的性质，正确判断对应角，对应边是解决本题的关键．在ABD △中，根据三角形内角和定理求得B ∠，根据全等三角形的对应角相等即可解决．【详解】解：在ABD △中，18025B BAD ADB ∠=︒-∠-∠=︒，∵AB AC =，BD CD =，AD AD =，∴()SSS ABD ACD ≌，∴25C B ∠=∠=︒．故选：A ．2．D【分析】本题主要考查了添加一个条件，使得用“SAS ”来判定△≌△AOB COD ，根据已知条件得出OA OC =，AOB COD ∠=∠，故只需要OB OD =即可使用SAS 证明△≌△AOB COD ．【详解】解：∵O 为AC 的中点，∴OA OC =，∵AOB COD ∠=∠，∴当添加OB OD =时，()SAS AOB COD ≌△△．故选：D ．3．B【分析】可以先证明ADE DCF ≌，则70ADF ∠=︒，利用角平分线可得35ADG ∠=︒，再利用直角三角形的两锐角互余解题即可．【详解】解：∵正方形ABCD∴90AD DC ADC C DAG AD BC ∠∠∠====︒ ，，，在ADE 和DCF 中，AD DC ADE C DE CF =⎧⎪∠=∠⎨⎪=⎩，∴ADE DCF≌∴70AED DFC ADF ∠∠∠===︒∵DG 平分ADF∠∴1352ADG ADF ∠∠==︒∴9055ADG ADG ∠∠=︒-=︒故选B ．【点睛】本题考查正方形的性质，全等三角形的性质和判定，掌握全等三角形的判定方法是解题的关键．4．A【分析】本题考查了全等三角形的判定与性质，三角形三边关系；证明ABD ECD ≌，得1CE AB ==，在AEC △中由三边不等关系确定AC 的取值范围，根据范围即可完成求解．【详解】解：D 为边BC 的中点，BD CD ∴=；在ABD △与BCD △中，BD CD ADB EDC AD DE =⎧⎪∠=∠⎨⎪=⎩，ABD ECD ∴ ≌，1CE AB ∴==；AE CE AC AE CE -<<+ ，4AE AD DE =+=，35AC ∴<<，故AC 可以为4,故选：A ．5．D【分析】本题主要考查了全等三角形的判定与性质、等底等高的三角形的面积相等、平行线的判定等知识点，熟练掌握三角形全等的判定方法并准确识图是解题的关键．根据三角形中线的定义可得BD CD =，然后利用“SAS ”证明BDF V 和CDE 全等，根据全等三角形对应边相等可得CE BF =，全等三角形对应角相等可得F CED ∠=∠，再根据内错角相等，两直线平行可得BF CE ∥，最后根据等底等高的三角形的面积相等判断出②正确．【详解】解：∵AD 是ABC 的中线，∴BD CD =，在BDF V 和CDE 中，BD CD BDF CDE DE DF =⎧⎪∠=∠⎨⎪=⎩，∴()SAS BDF CDE ≌ ，故④正确；∴CE BF F CED =∠=∠，，故①正确，∴BF CE ∥，故③正确；∵BD CD =，点A 到BD CD 、的距离相等，∴ABD △和ACD 面积相等，故②正确，综上所述，正确的是①②③④，共4个．故选：D ．6．B【分析】本题考查了全等三角形的判定与性质，互余．解题的关键在于对知识的熟练掌握与灵活运用．如图，证明()SAS ABC DFE ≌，则1BAC ∠=∠，由290BAC ∠+∠=︒，可得1290∠+∠=︒，然后作答即可．【详解】解：如图，∵BC ED =，90BCA DEF ∠=∠=︒，AC FE =，∴()SAS ABC DFE ≌，∴1BAC ∠=∠，∵290BAC ∠+∠=︒，∴1290∠+∠=︒，故选：B ．7．D【分析】本题考查尺规基本作图-作一角等于已知角，三角形全等的判定和性质，三角形外角的性质，根据作图，由全等三角形的判定定理SSS 可以推知DOE GCF ≌，得到GCF DOE ∠=∠，即48ACO AOB ∠=∠=︒，再利用三角形外角性质求解即可．【详解】解：由作图可知，在DOE 与GCF 中，OD CG DE GF OE CF =⎧⎪=⎨⎪=⎩，则()SSS DOE GCF ≌．∴GCF DOE ∠=∠，即48ACO AOB ∠=∠=︒，∴484896AHC AOB ACO ∠=∠+∠=︒+︒=︒．故选：D ．8．C【分析】易证≌ACD BCE V V ，由全等三角形的性质可知：A B ∠=∠，再根据已知条件和四边形的内角和为360︒，即可求出BPD ∠的度数．【详解】解：在ACD 和BCE 中，AC BC CD CE AD BE =⎧⎪=⎨⎪=⎩，∴()SSS ACD BCE ≌，∴BCE ACD ∠=∠，∴BCA ECD ∠=∠，∵55ACE ∠=︒，155BCD ∠=︒，∴100BCA ECD ︒∠+∠=，∴50BCA ECD ︒∠=∠=，∵55ACE ∠=︒，∴105ACD ∠=︒∴75A D ︒∠+∠=，∴75B D ∠+∠=︒，∵155BCD ∠=︒，∴36075155130BPD ︒︒︒︒∠=--=，故选：C ．【点睛】本题考查了全等三角形的判定和性质、三角形的内角和定理以及四边形的内角和定理，解题的关键是利用整体的数学思想求出75B D ∠+∠=︒．9．C【分析】先根据等腰直角三角形的性质可以得出ABE ACD ≌，属于手拉手型全等，所以()10414cm CD BE ==+=，最后根据时间=路程÷速度即可解答．本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．【详解】解：BAC EAD ∠=∠ ，BAC CAE EAD CAE ∴∠+∠=∠+∠，BAE CAD ∴∠=∠，在ABE 与ACD 中，AB AC BAE CAD AD AE =⎧⎪∠=∠⎨⎪=⎩，(SAS)ABE ACD ∴ ≌，10414(cm)CD BE BC CE ∴==+=+=，则()101424cm BC CD +=+= 壁虎以2cm/s 的速度B 处往D 处爬，24212()t s ∴=÷=．故选：C ．10．B【分析】根据三角形中线的定义可得BD CD =，然后利用“边角边”证明BDF 和CDE 全等，根据全等三角形对应边相等可得CE BF =，全等三角形对应角相等可得F CED ∠∠=，再根据内错角相等，两直线平行可得BF CE ，最后根据等底等高的三角形的面积相等判断出②正确．【详解】解：∵AD 是ABC 的中线，∴BD CD =，在BDF 和CDE 中，BD CD BDF CDE DF DE =⎧⎪∠=∠⎨⎪=⎩，∴()SAS BDF CDE ≌，故④正确∴CE BF F CED ∠∠==，，故①正确，∵CEF CED ∠∠=，∴CEF F ∠∠=，故⑤正确，∴BF CE ，故③正确，∵BD CD =，点A 到BD CD 、的距离相等，∴ABD 和ACD 面积相等，故②正确，综上所述，正确的有5个，故选：B ．【点睛】本题考查全等三角形的判定与性质，熟练掌握全等三角形的判定方法并准确识图是解题的关键．11．BD CD=【分析】本题主要考查对全等三角形的判定的理解和掌握，根据用“SAS ”判定ABD ACD △≌△，已知12∠=∠及公共边AD ，添加的条件是BD CD =．【详解】解：添加的条件是BD CD =，理由是：在ABD △与ACD 中，11AD AD BD CD =⎧⎪∠=∠⎨⎪=⎩，∴()SAS ABD ACD ≌，故答案为：BD CD =．12．25︒/25度【分析】本题主要考查了全等三角形的性质与判定，三角形内角和定理，证明()SSS ABC ADE ≌得到AED C ∠=∠，再根据三角形内角和定理和平角的定义可得2125∠=∠=︒．【详解】解：∵AD AB =，AE AC =，DE BC =，∴()SSS ABC ADE ≌，∴AED C ∠=∠，∵11802C AEC AEC AED ∠++=︒=++∠∠∠∠∠，∴2125∠=∠=︒，故答案为：25︒．13．SAS /边角边【分析】本题考查了全等三角形的判定，根据SAS 即可证明ACB ACD ≌ 是解题的关键．【详解】解：AC BD ^ ，90ACB ACD ∴∠=∠=︒，在ACB △和ACD 中，AC AC ACB ACD BC CD =⎧⎪∠=∠⎨⎪=⎩，()SAS ACB ACD \≌ ，故答案为：SAS ．14．117︒/117度【分析】本题考查了全等三角形的判定及其性质等知识，根据平行线的性质得出∠=∠ABC BED ，进而利用SAS 证明ABC 和EBD △全等，利用全等三角形的性质解答即可．【详解】解：∵DE AB ∥，ABC BED ∴∠=∠，在ABC 和EBD △中，BA BE ABC BED BC DE =⎧⎪∠=∠⎨⎪=⎩，()SAS ABC EBD ∴ ≌，38BAC EBD ∴∠=∠=︒，1801803825117BDE EBD E ∴∠=︒-∠-∠=︒-︒-︒=︒，故答案为：117︒．15．100【分析】本题考查了三角形全等的判定与性质，熟练掌握三角形全等的判定方法是解题关键．先证出EBD ABD △≌△，再根据全等三角形的性质可得80BED A ∠=∠=︒，由此即可得．【详解】解：在EBD △和ABD △中，ED AD BE BA BD BD =⎧⎪=⎨⎪=⎩，()SSS EBD ABD ∴ ≌，80BED A ∴∠=∠=︒，180100DEC BED ∴∠=︒-∠=︒，故答案为：100．16．4或245【分析】本题主要考查三角形全等的判定．设运动s t ，则4 cm AP t =，()204cm BP AB AP t =-=-， cm BQ vt =，由于在长方形ABCD 中，90A B ∠=∠=︒，因此①当AE BP =，AP BQ =时，()SAS AEP BPQ ≌，②当AE BQ =，AP BP =时，()SAS AEP BQP ≌，代入即可求解v 的值．【详解】设运动s t ，则4 cm AP t =，()204cm BP AB AP t =-=-， cm BQ vt =，∵在长方形ABCD 中，90A B ∠=∠=︒，∴①当AE BP =，AP BQ =，即12204t =-，4t vt =时，()SAS AEP BPQ ≌，解得：2t =，4v =或当AE BQ =，AP BP =，即12vt =，4204t t =-时，()SAS AEP BQP ≌，解得：52t =，245v =．综上所述，v 的值为4或245．故答案为：4或24517．10【分析】本题考查了全等三角形的判定与性质，解决本题的关键是证明ACD ECD ≌△△，在BC 边上取点E ，使EC AC =，连接DE ，证明ACD ECD ≌△△，再根据已知条件证得6BD BE ==，即可得解．【详解】解：如图，在BC 边上取点E ，使EC AC =，连接DE ，∵CD 平分ACB ∠，∴ACD ECD ∠=∠，∵CD CD =，∴()SAS ACD ECD ≌，∴4AC CE ==，ADC EDC ∠=∠，∵22A ADC ADE ADC EDC ADC ∠=∠∠=∠+∠=∠，，∴A ADE DEC ∠=∠=∠，∴BDE BED ∠=∠，∴6BD BE ==，∴6410BC BE CE =+=+=．故答案为：10．18．1802x-【分析】本题主要考查了全等三角形的判定与性质，角平分线的性质，利用SAS 证明ABC ADC △△≌得D DCA B BCA ∠+∠=∠+∠，根据三角形的外角定理推出B BCA CAE ∠+∠=∠，进而根据三角形内角和定理即可求解，解题的关键是利用SAS 证明ABC ADC △△≌．【详解】解：∵AC 平分DCB ∠，∴BCA DCA ∠=∠，在ABC 和ADC △中,CB CD BCA DCA CA CA =⎧⎪∠=∠⎨⎪=⎩∴ABC ADC △△≌，∴B D ∠=∠，∴B BCA D DCA ∠+∠=∠+∠，∵EAC D DCA ∠=∠+∠，∴B BCA EAC ∠+∠=∠，∵180180B BCA BAC BAE EAC ∠+∠=︒-∠=︒-∠-∠，∴180CAE BAE EAC ∠=︒-∠-∠，∵BAE x ∠=︒，∴1802x EAC -⎛⎫∠=︒ ⎪⎝⎭，故答案为：1802x -．19．见解析【分析】由BE CF =可得BF CE =，然后利用SSS 证明ABF DCE ≌即可证明结论．【详解】解：∵BE CF =，∴BE EF EF FC +=+，即BF CE =，在ABF 和DCE 中AB CD AF DE BF CE =⎧⎪=⎨⎪=⎩，∴ABF DCE ≌，∴B C ∠=∠．【点睛】本题考查全等三角形的判定和性质，掌握全等三角形的判定方法是解题的关键．20．(1)见解析(2)见解析【分析】本题考查了全等三角形的判定与性质，解题的关键是：（1）利用SSS 证明ABC DEF ≌△△，然后根据全等三角形的性质即可得证；（2）利用AAS 证明ABO DEO △△≌，然后根据全等三角形的性质即可得证．【详解】（1）证明：∵BF CE =，∴BC EF =，在ABC 和DEF 中AB DE BC EF AC DF =⎧⎪=⎨⎪=⎩，∴()SSS ABC DEF ≌，∴B E ∠=∠；（2）证明：在ABO 和DEO 中B E AOB DOE AB DE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()AAS ABO DEO ≌，∴AO DO =，=BO EO ，即AD ，BE 互相平分．21．(1)见解析(2)25E ∠=︒【分析】本题主要考查了全等三角形的判定与性质；（1）根据题意由DAB BAC CAE BAC ∠+∠=∠+∠，可得DAC BAE ∠=∠，即可求证；（2）由()SAS BAE DAC ≌，可得E C ∠=∠，再由内角和为180︒即可求解．【详解】（1）证明：∵DAB CAE ∠=∠，∴DAB BAC CAE BAC ∠+∠=∠+∠，∴DAC BAE ∠=∠，又∵AD AB AC AE ==，，∴()SAS BAE DAC ≌；（2）∵()SAS BAE DAC ≌，∴E C ∠=∠，∵13520CAD D ∠=︒∠=︒，，∴1801801352025C CAD D ∠=︒-∠-∠=︒-︒-︒=︒，∴25E C ∠=∠=︒．22．(1)见详解(2)65︒【分析】本题考查了全等三角形的性质和判定、平行线的性质和判定、三角形内角和定理等知识点，能综合运用定理进行推理是解此题的关键．（1）求出AED CEF ≌，根据全等三角形的性质得出A ACF ∠=∠，根据平行线的判定得出即可；（2）根据（1）求出A ACB ∠=∠，根据三角形内角和定理求出即可．【详解】（1）证明：∵E 为AC 中点，AE CE ∴=，在AED △和CEF △中AE CE AED CEF DE EF =⎧⎪∠=∠⎨⎪=⎩，()AED CEF SAS ∴ ≌，A ACF ∴∠=∠，∴CF AB ∥；（2）解：∵AC 平分BCF ∠，ACB ACF ∴∠=∠，A ACF ∠=∠ ，A ACB ∴∠=∠，180,50A ABC ACB ABC ∠+∠+∠=︒∠=︒ ，18050652A ︒-︒∴∠==︒，65A ∴∠=︒．23．(1)CE CD BC+=(2)不成立．CE CD BC-=【分析】本题考查的是全等三角形的判定与性质，掌握全等三角形的判定方法是解本题的关键．（1）证明BAD CAE ∠=∠．再证明()SAS BAD CAE ≌△△，可得CE BD =，再进一步可得结论；（2）证明BAD CAE ∠=∠．再证明()SAS BAD CAE ≌△△，可得CE BD =，再进一步可得结论；【详解】（1）解：∵BAC DAE ∠=∠，∴BAC DAC DAE DAC ∠-∠=∠-∠，即BAD CAE ∠=∠．在BAD 与CAE V 中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，∴()SAS BAD CAE ≌△△，∴CE BD =，∴CE CD BD CD BC +=+=．（2）不成立．CE CD BC -=．理由：∵BAC DAE ∠=∠，∴BAD CAE ∠=∠．在BAD 与CAE V 中，,,,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩()SAS BAD CAE ∴△≌△，∴CE BD =，∴CE CD BD CD BC -=-=．24．（1）见解析（2）2EF AD =，理由见解析【分析】本题考查了全等三角形的判定和性质、平行线的判定和性质，熟练掌握知识点、推理证明是解题的关键．（1）根据AD 是边BC 的中线，得出BD CD =，利用SAS 证明GDB ADC ≌，得出DBG ACD Ð=Ð，根据“内错角相等，两直线平行”，即可证明AC BG ∥；（2）由（1）得AC BG ∥，GDB ADC ≌，得出180BAC ABG ∠+∠=︒，BG AC =，推出BG AF =，ABG EAF ∠=∠，利用SAS 证明ABG EAF ≌，得出AG EF =，根据DG AD =，AG DG AD =+，得出2AG AD =，即可证明2EF AD =．【详解】解：（1）∵AD 是边BC 的中线，∴BD CD =，在GDB △和ADC △中，DG AD GDB ADC BD CD =⎧⎪∠=∠⎨⎪=⎩，∴()SAS GDB ADC ≌，∴DBG ACD Ð=Ð，∴AC BG ∥；（2）2EF AD =，理由如下，∵由（1）得AC BG ∥，GDB ADC ≌，∴180BAC ABG ∠+∠=︒，BG AC =，∵AC AF =，∴BG AF =，∵3603609090180BAC EAF BAE CAF Ð+Ð=°-Ð-Ð=°-°-°=°，∴ABG EAF ∠=∠，在ABG 和EAF △中，AB AE ABG EAF BG AF =⎧⎪∠=∠⎨⎪=⎩，∴()SAS ABG EAF ≌，∴AG EF =，∵DG AD =，AG DG AD =+，∴2AG AD =，∴2EF AD =．。