下载文档原格式
图像处理中的小波变换算法及应用随着计算机技术的不断进步和发展，图像处理技术也得到了极大地提升和拓展。
小波变换作为一种新颖、实用的信号分析方法，已经广泛地应用于各种领域，特别是在图像处理领域中更是如此。
本文将介绍小波变换算法的基本概念、原理和应用。
一、小波变换算法的基本概念小波变换（Wavelet Transform）是一种基于时间-频率分析的数学工具，起源于哈尔小波，它可以将时间和频率分隔开来，可以生成比傅里叶变换更加精细的图像，更加精确地反映了信号的时间和频率信息。
小波分析的关键是选用不同的小波基函数（Wavelet Function）。
小波基函数是一个数学函数，通过不同的小波基函数的组合可以快速地对信号进行分解和重构。
小波基函数通常有多种不同的类型，如海涅小波、Daubechies小波、Symmlet小波等，每个类型又包含了不同的级别，即小波基函数的阶数，用于调整小波分析的分辨率和精度。
二、小波变换算法的原理小波变换算法包括离散小波变换（DWT）和连续小波变换（CWT）两种类型。
离散小波变换是对离散信号进行分析的，而连续小波变换则是用于连续信号分析。
在这里，我们主要介绍离散小波变换算法。
离散小波变换将原始信号分解成一组小波基函数的线性组合，每个小波基函数对应一个不同的频率，这样可以对信号进行不同尺度的分析。
小波分解的过程可以采用多层分解的方式，每一层分解后得到的是一个低频分量和一个高频分量，然后将低频分量再进行分解，直到分解到指定的层数为止。
连续小波变换通过将信号与窗口函数进行卷积得到小波系数，进而得到频谱。
它的计算方式与傅里叶变换类似，但连续小波变换可以同时提供时间和频率信息，更加适合于非平稳信号的分析。
三、小波变换算法的应用小波变换算法在图像处理中的应用非常广泛，例如：1. 压缩。
小波变换可以将信号分解为不同的频率分量，可以通过选择保留重要的分量来达到压缩的效果。
小波变换的压缩效果比傅里叶变换更加优秀，同时也可以将信号进行逐步近似，得到不同精度的压缩结果。
数字图像处理中的小波变换数字图像处理是一门处理和分析数字图像的学科，可以应用于许多领域，如医学影像、遥感图像以及计算机视觉等。
在图像处理的过程中，小波变换是一种重要的技术，具有较好的时频局部特性，能够有效地揭示图像内容的细节和模式。
本文将介绍数字图像处理中的小波变换原理以及其应用。
一、小波变换原理小波变换是一种多尺度分析方法，通过不同尺度的小波函数对信号进行分解与重构。
它具有时频局部性的特点，能够捕捉到信号的瞬时特征和频率特征，并能够精确地表示信号的时域和频域信息。
小波变换的计算过程可以分为两个步骤：分解和重构。
在分解过程中，根据小波变换的特性，将原始图像分解成一系列的低频分量和高频细节；在重构过程中，利用分解得到的低频分量和高频细节重构出与原始图像相同的图像。
二、小波变换的应用1. 图像压缩与编码小波变换在图像压缩和编码中有着广泛的应用。
通过对图像进行小波分解，可以将图像信号分解成高频和低频分量，其中低频分量包含图像的主要信息，而高频分量则包含图像的细节信息。
通过对高频分量进行量化和编码，可以实现对图像的高效压缩，并保持较好的视觉质量。
2. 图像增强与去噪小波变换可以通过分解图像和重构图像的方式实现图像的增强和去噪。
在小波分解时，图像的高频细节部分可以提供图像的纹理和边缘特征，通过调整高频部分的权重系数，可以对图像进行增强处理。
同时，利用小波变换的多尺度分析特性，可以将图像的噪声分解到不同的尺度中，从而实现对图像的去噪效果。
3. 图像特征提取与分析小波变换可以提供图像的时频局部特性，对于图像的特征提取和分析有着重要的作用。
通过对图像的小波分解，可以获取到不同尺度的小波系数，其中较大的系数对应于图像的明显特征，如纹理、边缘和斑点等。
通过对小波系数的分析和处理，可以实现对图像的特征提取和分类，为图像识别和目标检测等任务提供有效的手段。
三、小波变换的发展与应用前景随着数字图像处理技术的不断发展，小波变换在图像处理中的应用也得到了广泛的推广和应用。
小波分析系列讲座5以图像来说明建立空间特征基和小波变换的关系设有一幅图像，从不同分辨率考察。
若我们离很远来看，可能会把每64个点看作一个点，若记此时构成的描述空间为V0.若走进一些，把16个点看作一个点，记此时构成的描述空间为V1若再走进一些，把4个点看作一个点，记此时构成的描述空间为V2若再走进一些，把1个点看作一个点，记此时构成的描述空间为V3则可知凡是Vi空间内可以描述的图像，Vi+1空间内皆可描述,并且描述的更细致故Vi包含于Vi+1空间记Vi+1=Vi+Wi ,即Vi和Wi构成Vi+1空间。
（若Vi⊥Wi ，则Wi为Vi的正交补空间，实际应用中不要求一定正交。
）( ⊥ 正交) 则Vi+1=Vi+Wi=Vi-1+Wi-1+Wi=……记Pi为图像在Vi空间的描述则Di= Pi+1 - Pi 就表示了图像在这两个描述空间的细节差异，因为Vi+1=Vi+Wi，故Di为图像在Wi空间上的描述。
即Wi空间表述了细节差异。
如果Wi⊥Wj, 并且在Wj空间中能找到一组正交标准基，其基本函数必是高（带）通的，就称其为小波函数。
Wi⊥Wj正交，即为不同分辨率下的细节差异不相关，从而消除冗余。
那么例子中V3=W2+W1+W0+V0相应得到 P3=D2+D1+d0+P0即最清晰分辨率下的图像可以有不同分辨率下的细节差异和最高分辨率下的图像合成而得由概率特性知细节差异在大范围内是一个较小的值。
如果用上节所引入的频域概念来看，低频信息就是P0,高频为Di,这里的低频和高频就和傅里叶有稍微不同。
而从分析中，我们自然而然的知道随着频率的不同，其数值对应的空间窗口大小也不同了。
正好满足上节所说。
呵呵，剩下的分析任务就是如何构造Wi。
§3-5 示波器的使用阴极射线示波器是一种用途较为广泛的电子仪器，它可以把原来肉眼看不见的电压变化变换成可见的图像，以供人们分析研究。
示波器可用来测量电压的大小和一切可转换为电压的电学量(如电流、电功率、阻抗等)和非电学量(如位移、速度、压力、频率、温度、磁场、光强等)。
在无线电制造工业和电子测量技术等领域，它是不可缺少的测试设备。
一、实验目的1. 了解示波器的基本结构，熟悉示波器的调节和使用。
2. 学习用示波器观察电压波形及测量信号的电压和周期。
3. 通过观察李萨如图形，学会用示波器测量频率的方法。
二、实验仪器示波器(GOS-620双轨迹示波器)、函数信号发生器、波形整流仪。
函数信号发生器的作用是产生各种波形、频率的电信号。
整流波形仪的功能是将50Hz 的照明电变成脉动直流电以及稳恒直流电。
这些仪器的面板图请参见本实验的附录部分。
三、实验原理示波器动态显示物理量随时间变化的思路是将这些物理量转换成随时间变化的电压，加在电极板上，极板间形成相应的变化的电场，使进入这个变化电场的电子运动情况相应的随时间变化，最后把电子运动的轨迹用荧光屏显示出来。
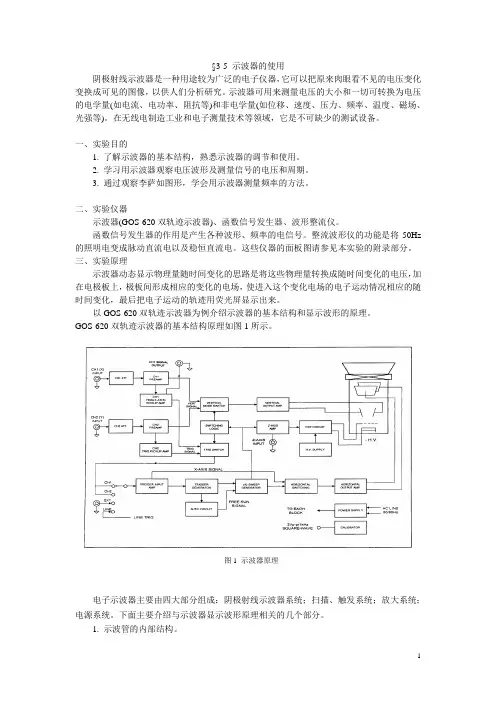
以GOS-620双轨迹示波器为例介绍示波器的基本结构和显示波形的原理。
GOS-620双轨迹示波器的基本结构原理如图1所示。
电子示波器主要由四大部分组成：阴极射线示波器系统；扫描、触发系统；放大系统；电源系统。
下面主要介绍与示波器显示波形原理相关的几个部分。
1. 示波管的内部结构。
图1 示波器原理示波管内部结构如图2所示。
阴极被加热发射出大量电子，经过各个电极的聚焦、加速后高速轰击荧光屏，发生荧光。
在靠近阴极处设置控制栅极，调节其电位(相对阴极为负电位)来控制电子束流的强度，使荧光“辉度”改变。
在电子束路径两旁设置两对平行板电极，改变加在其上的电压，可控制电子束的运动。
2. 电偏转系统。
在示波管内，有两对平行板电极，垂直方向的一对平行板电极称为水平(或x )偏转板，简称为横偏板。
《信息隐藏实验教程》教学幻灯片7\+小波与小波变换简述通俗的讲，小波（wavelet）是一种在有限Jr牛農矍，内番歸翘番爲勰穌翳零的特殊波形。
很设存在一个时域函数（P⑴，满足：/ _4（/）0①⑷）（f表示fourier变换）f （p{t）dt =0或52-do) V+R O)小波与小波变换简述则称(p⑴为一个母小波函数(Mother Wavelet Function)o 一个母小波函数有文口下几个特点：1.因为妙(少)=/申0疋叫h而，匚= 0 故而①(0)=匸倾M = 也就是盏，一个母小波函数的直流分量(Direct current components)为0。
换句话说，就是母小波函数具有正负交替的特点, 其均值为0。
2• —个母小波函数是一个带通信号。
小波与小波变换简述3 •母小波函数随I绝对值的变大而最终衰减为0。
即其函数表达式具有紧支集。
下图是典型的小波母函数和小波函数。
V11二维信号的小波分解就可以写为：4 yg〉，) = y) + D'jfg y) + D~f(x, y) + D^f{x, y)其中A为低频分量，D可以看为水平、垂直和对角三个方向上的高频分量。
/ /£图像小波变换这里，我们选用的二维图像信号仍然是lenna.jpg O由于lenna是一个RGB图像, 我们仅对其R层进行实验。
编写函数wavelet2D.m来完成央验。
实验结果如下图所示。
却像小波变换 古图像小波变换古图像小波变换清晰的反映了两重小波分解后的各个频率 段信号重构成的图像。
可以发现，低频图像与 原始图像是非常近似的，而高频部分也可以认 为是冗余的噪声部分。
所以，图像载体下的小 波分解信息隐藏算法一般的都是将信息隐藏于 分解后的低频部分，从而获得高的鲁棒性。
当 然的，将信息隐藏于高频系数中，可以获得很 好的不可见性.不可见性与鲁棒性是信息隐藏是一对矛盾。
解决这一矛盾的方法是“折衷‘‘。
算法性能好坏的重要判定依据，二者可以看成 2尺FPffni •减羅8弋《夸丄宀最后，我但来#一下这些频率＞數的具依内容：lennaR是一个256 x 256的二维信号，对其做1层小波分解，得到C是一个1 X 65536的行 ,记录的是低频、水平高频、垂直高频和高频）四个部分的累数。
