当前位置：文档之家 › 连续介质力学第一章.

连续介质力学第一章.

  • 格式：ppt
  • 大小：312.00 KB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

第1章连续体力学知识讲解

第1章连续体力学知识讲解

第1章连续体力学第一章 连续体力学思考题1-1 在固体的形变中，弹性模量是一个重要的参数。

杨氏模量的物理意义是什么？答：对于一般的固体材料，若形变不超过一定的限度，应力与相关的应变成正比。

在拉伸应变中l l Y∆＝拉σ 其中，比例系数Y 称为杨氏模量。

弹性模量实际上反映了材料对形变的抵抗能力。

在拉伸应变中，杨氏模量反映了材料对拉伸形变的抵抗能力。

1-2 生物材料的应力～应变关系与一般固体的应力～应变关系有什么不同？ 答：晶体材料的原子排列很有规则，原子间的键合比较紧密，可以产生较大的应力，杨氏模量一般较高；而生物材料绝大多数是由非均匀材料组成的聚合物，这些聚合物的长链大分子互相纠缠在一起，彼此之间相互作用较弱。

当受到外力拉伸时，不仅生物材料的分子本身可以伸长，而且分子之间也容易发生滑动，杨氏模量相对较小。

1-3 液体的表面张力与橡胶弹性膜的收缩力有什么不同？答：前者来源于分子间的吸引力，后者来源于分子的形变；前者只存在于液体表面，后者存在于发生应变的弹性膜的整个横截面上。

1-4 图1-1中表示土壤中的悬着水，其上、下两液面都与大气接触。

已知 上、下液面的曲率半径分别为A R 和B R (B R >A R )，水的表面张力系数为γ，密度为ρ。

问悬着水高度h 为多大？解：在上液面下取A 点，设该点压强为A p ，在下液面内取B 点，设该点压强为B p 。

对上液面应用拉普拉斯公式，得AA R p p γ20=- 对下液面使用拉普拉斯公式，得 BB 02R p p γ=- 图1-1 土壤中的悬着水 又因为gh p p ρ+=A B 将三式联立求解可得 ⎪⎪⎭⎫ ⎝⎛-=B A 112R R g h ργ1-5 在自然界中经常会发现一种现象，在傍晚时地面是干燥的，而在清晨时地面却变得湿润了。

试解释这种现象的成因。

答：由于水的表面张力系数与温度有关，毛细水上升的高度会随着温度的变化而变化，温度越低，毛细水上升的高度越高。

第一章 连续体力学

第一章 连续体力学

（5）液晶态：在一定温度下，晶体变成清亮透明的液态。
特点：1）力学性质象液体。 2）光学性质象晶体。
4
二、应变与应力
1、应变：物体在外力作用下发生的相对形变。
5
2、两种基本形变： 拉伸压缩：在外力牵引或压缩下发生长度的变化。 剪切形变：在外力偶作用下，两个平行截面间发生 相对平移，只有形状变化而没有体积变化的形变。
p 1.46 10 ，46 10 ，46 10 pa 1. 1.
4 5 6
38
应用：毛细现象 Capillary
浸润液体在细管里上升和不浸润液体在细管里 下降的现象，称为毛细现象
管内液面上升的高度
2 cos h gr
39
【例4】汞对玻璃表面完全部润湿，若将直径为0.100mm的 玻璃毛细管插入大量汞中，试求管内汞面的相对位置。已 知汞的密度1.35×10-4Kg.m-3，表面张力0.520N.m-1。 解：完全不润湿时，cosθ=-1,
32
四、弯曲液面两侧压强差
33
1 、浸润与不浸润
接触角：在液体与 固体接触处，作液 体表面的切线与固 体表面的切线，这 两条切线通过液体 内部所成的角度θ 称为“接触角”。
/2 /2
液体润湿固体
液体不润湿固体
0
完全润湿
完全不润湿
34

2、拉普拉斯公式(掌握)
凸球形液面内外压强差
2 2 0.520 10 2 h 1.35 10 4 9.8 0.05 10 3 cm gR h -15.7cm
40
毛细现象的例子
下雨后，人走过潮湿的泥地，在地面上留下的脚 印里会渗出水来 建房子时在地基上铺防潮毡 画国画，毛笔由于有毛细管可吸较多墨汁，宣纸 由于毛细管的作用能使墨汁迅速散布开来

连续介质力学作业(第一章参考答案)

连续介质力学作业(第一章参考答案)

(
)
5
x ⋅ S ⋅ x = xm g m ⋅ =
1 ij S − S ji g i g j ⋅ xn g n 2
(
)
1 ij S − S ji xm x n g m ⋅ g i g j ⋅ g n 2 1 = S ij − S ji xm xn δim δ n j 2 1 1 = S ij xi x j − S ji xi x j 2 2 1 1 = S ij xi x j − S ji x j xi 2 2 1 1 = S ij xi x j − S ij xi x j 2 2 =0
其他两个，同理可证。 (1)如果二阶张量 S 是反对称张量，对于任意一阶张量 x ，证明 x ⋅ S ⋅ x = 0 (2) S 是二阶反对称张量， A 是二阶对称张量，证明 A : S = 0
5.
¾

解答：
m
（1） x = xm g
因为二阶张量 S 是反对称张量
S=
1 ij S − S ji g i g j 2
(
)
(
)
（2） S = S g i g j ， A = Amn g g ，
ij m n ij A : S = S ij g i g j : Amn g m g n = S ij Amn δim δ n j = S Aij
S ij Aij = − S ji Aij = − S ji A ji = − S ij Aij
c） R ε g R = ε l 所以
T
1 ⎤ ⎥ 2 ⎥ ⎡1.6 ⎢ 3 ⎥⎣ 0 2 ⎥ ⎦
⎡ 0 ⎤⎢ ⎢ 2.3⎥ ⎦⎢ ⎢ ⎣
3 2 1 2
1⎤ − ⎥ ⎡ 1.775 0.3031⎤ 2⎥ = ⎢ ⎥ 3 ⎥ ⎣0.3031 2.125 ⎦ 2 ⎥ ⎦

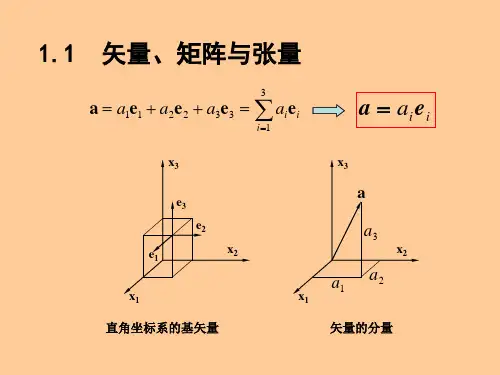
连续介质力学-第1章-四川大学复习过程

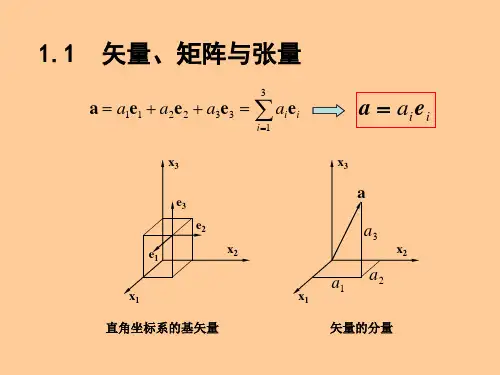
连续介质力学-第1章-四川大学复习过程
偶排列: 123，231，312
奇排列: 132，213，321
c a b (aiei ) (b j e j ) ijk aib j ek
ei e j ijk ek
ab ba
a b b a
(5) 混合积
[a，b，c] a (b c)
如果a、b、c的空间位置顺序服
c
从右手螺旋法则，那么混合积的几
kk 3
kn ik ni
小结：
➢ Einstein求和约定 a ai ei
➢ Kronecker记号
ij
1 0
(i j) (i j)
➢ 置换符号
1
ijk 1
0
(当ijk是123的偶排列时) (当ijk是123的奇排列时) (当ijk有两个值相等时)
➢ 自由标，哑标
1.2 场论概要
1 ei e j 0
(i j) (i j)
ij
1 0
(i j) (i j)
Kronecker记号 ij
11 22 33 1
12 21 23 32 13 31 0
a b (aiei ) (bje j ) aibj (ei e j ) ij aibj aibi
偶排列与奇排列：
方法一： 123是偶排列；
当一个排 列1 从12(3当开ij始k是交1换23的相偶邻两排个列数时)的位置，
置换符号 若数需次ijk要则交 是换偶01 奇排数列次。((当当则iijj该kk是有排1两2列3个的是值奇奇相排排等列列时时，))交换偶
方法二：
1
2
3
方法三 ：ijk 死 记jki 硬背 kij ijk jik ikj kji
1.1 矢量、矩阵与张量
3

连续介质力学

连续介质力学

b1
=
1 H1
g1
bi
=
1 Hi
gi
b2
=
1 H2
g2
b3
=
1 H3
g3
则 bi 为正交曲线坐标系的标准化正交基。
因此，显然有
ei
⋅ej
=
bi
⋅bj
= δij
=
⎧1 ⎨⎩0
i= j i≠ j
（2.1.4） （2.1.5）
质量守恒定律（非相对论，牛顿力学观点）； 能量守恒（热力学定律）； 有限变形及连续性条件（几何方程）。 2）材料本构方程 不同材料具有不同特性是材料属性，这属性称为本构属性。本构属性的描述为本构方 程。在本课程中，只讨论本构方程的框架（形式）。 具体本构方程只有通过实验得出，本构方程包含：①应力、应变关系；②材料常数。 本课程中，研究本构方程框架所应用的基本理论为： ① 基本连续介质热力学的内变量理论； ② 基于理性化公理的本构方程原理。 所得到的本构方程框架具有本构方程的指导原则。 非线性方面在下面两个方面反映： ① 有限变形—称为几何非线性。 ② 本构方程非线性—称为物理（材料）非线性。 若同时考虑以上两个方面的非线性因素，则称为双非线性问题。
2．空间的维数
设α i 为 m 个标量，若能选取α i ，使得
m
∑αiai = 0
i =1
（2.1.1）
且α i 不全为零，则称此 m 个矢量线性相关，否则，称为线性无关。
例 1 位于同一平面内的两个矢量 a1 和 a2 （如图
2.1.1）是线性无关的，即
a1
α1a1 + α2a2 ≠ 0 （α1 和α 2 可为任意值，
3．本课程的特点
① 普遍性； ② 严密性（只有一个基本假设，物理定律和公理作为依据）； ③ 溶入于连续介质热力学； ④ 对连续介质的本构方程作框架的理论研究。

连续介质力学-例题与习题

连续介质力学-例题与习题

《连续介质力学》例题和习题第一章 矢量和张量分析第一节 矢量与张量代数一、矢量代数令112233A A A =++A e e e ,112233B B B =++B e e e ,则有112233A A A αααα=++A e e e111222333()()()A B A B A B +=+++++A B e e e112233112233112233()()A A A B B B A B A B A B •=++•++=++A B e e e e e e112233112233111112121313212122222323313132323333()() A A A B B B A B A B A B A B A B A B A B A B A B ⨯=++⨯++=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯A B e e e e e e e e e e e e e e e e e e e e e e e e又因为: 11⨯=e e 0;123⨯=e e e ;132⨯=-e e e ;213⨯=-e e e ;22⨯=e e 0;231⨯=e e e ; 312⨯=e e e ;321⨯=-e e e ;33⨯=e e 0则: 233213113212213(_)()()A B A B A B A B A B A B ⨯=+-+-A B e e e 习题:1、证明下列恒等式：1）[]2()()()()⨯•⨯⨯⨯=•⨯A B B C C A A B C2) [][]()()()()⨯•⨯=•⨯-•⨯A B C D A C D B B C D A2、请判断下列矢量是否线性无关？1232=-+A e e e 23=--B e e 12=-+C e e .其中i e 为单位正交基矢量。

3、试判断[]816549782-⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦A 是否有逆矩阵；如有，请求出其逆阵[]1-A 。

二、张量代数例1：令T 是一个张量，其使得矢量a ，b 经其变换后变为2=+Ta a b ，=-Tb a b ，假定一个矢量2=+c a b ，求Tc 。

Chap 1 连续体力学

Chap 1 连续体力学

R = r cosθ
2γ cosθ h= ρgr
3. 应用:植物的水分运输 植物的水分运输
§3 理想流体的流动
(Fluidity of ideal fluid)
一、基本概念
1. 理想流体（ideal fluid）
不可压缩的没有黏滞性的流体称理想流体 理想化方法与理想模型
2. 稳定流动（steady flow）
应力伴随应变的增大而增大， 应力伴随应变的增大而增大，它反映了发生形变的物 体内部的紧张程度。对于一般的固体材料， 体内部的紧张程度。对于一般的固体材料，若形变不超过 一定的限度，应力与相关的应变成正比，此称胡克定律 胡克定律。 一定的限度，应力与相关的应变成正比，此称胡克定律。 拉伸应变
σ 拉＝E
2.29×10－2 × 2.9×10－2 × 49.0×10－2 × 1.65×10－2 × 6.5×10－2 × 2.5×10－2 ×
/N•m-1
3. 影响表面张力系数的因素 液体种类
∆F
温度 表面活性物质 4. 表面张力的成因 5. 表面张力的测量
∆l
例题： 当许多半径为r的小水滴融合成一个半径为 的小水滴融合成一个半径为R的大 例题： 当许多半径为 的小水滴融合成一个半径为 的大 水滴时释放出的能量。假设水滴呈球状， 水滴时释放出的能量。假设水滴呈球状，水的表面张力 系数在此过程中保持不变。 系数在此过程中保持不变。 解：设小水滴的数目为N，融合过程中释放出的能量 设小水滴的数目为 ， 为水滴表面积减小时所减小的表面能。 为水滴表面积减小时所减小的表面能。由于融合前后水 滴的总体积保持不变， 滴的总体积保持不变，则
yy
df df p= = ρ gy dS
即 b
dy

连续介质力学-第1章-四川大学

连续介质力学-第1章-四川大学

[a，b，c] [b，c，a] [c，a，b] [a，b，c] [b，a，c] [c，b，a] [a，c，b]
例:导出Kronecker符号与置换符号间的运算关系。
11 12 13 21 22 23 1 31 32 33
1i 1 j 1k ijk 2i 2 j 2k
(2) 数乘
a b (b j e j ) (b j )e j
(3) 数积
a b (ai ei ) (b j e j ) aibi a1b1 a2b2 a3b3
a b (ai ei ) (b j e j ) aibi a1b1 a2b2 a3b3
km kn kk
ijk mnk kkim jn jm kn ik kmin jk im kn jk kk jmin km jn ik 3im jn jm kn ik kmin jk im kn jk 3 jm in km jn ik 3im jn jm ni mjin im nj 3 jm in mi jn
➢矢量的旋度仍为矢量，是空间坐标点的函数
➢一点的旋度的大小是该点环量面密度的最大值。
➢旋度的方向是与该点最大环量面密度对应的法线方 向。
在矢量场中，若rot u＝J≠0，称之为旋度场(或涡旋场 )，J 称为旋度源(或涡旋源)，若矢量场处处rotu＝0 ，称之为无旋场。
小节：
梯度： grad u u
Einstein求和约定
哑标: 求和约定中的重复脚标
哑标可以用其它的字母代替，只要该字母在本项中 没有出现过就行
a aiei a je j

第一章2连续介质力学

第一章2连续介质力学

⎡e1′ ⋅ e1 M = ⎢⎢e′2 ⋅ e1
⎢⎣e3′ ⋅ e1
e1′ ⋅ e2 e′2 ⋅ e2 e3′ ⋅ e2
e1′ ⋅ e3 ⎤ ⎡cos(e1′，e1 )
e′2
⋅
e3
⎥ ⎥
=
⎢⎢cos(e′2，e1
)
e3′ ⋅ e3 ⎥⎦ ⎢⎣cos(e3′，e1 )
cos(e1′，e2 ) cos(e′2，e2 ) cos(e3′，e2 )
A
A
A
J′ = MJMT
例1.26 证明： ∇v 是二阶张量。
解：
∇v
=
ei
∂ ∂xi
(v je j )
=
v j，i ei e j
xi = M mi xm′
∂xi ∂xm′
= M mi
vn′ = M nj v j
∂vn′ ∂xm′
= ∂vn′ ∂xi
∂xi ∂xm′
=
∂(Mnjvj ∂xi
)
Mmi
cos(e1′，e3 )⎤ cos(e′2，e3 )⎥⎥ cos(e3′，e3 )⎥⎦
b = (e1′ e′2 e3′ ) b′ = (e1 e2 e3 ) b b = (e1′ e′2 e3′ ) b′ = (e1 e2 e3 ) MT b′ = (e1 e2 e3 ) b
b = MTb′
b′ = Mb
定义：基矢量ei和ej可作并积，而形成二阶单位并矢量eiej
∇v = 2x1e1e1 + x2e1e2 + 4x2e2e1 + (x1 + 2x2 )e2e2
∇v = (e1
e2 )⎢⎣⎡42xx12
x2 ⎤ ⎡e1 ⎤

连续介质力学作业(第一章)答案

连续介质力学作业(第一章)答案

连续介质力学作业（第一章）习题1. 向量~~~~k z j y i x a ++=。

~i ，~j ，~k 表示三维空间中标准正交基。

给定一组协变基~~12i g =，~~~2j i g +=，~~~3k j g +=。

（1）求逆变基1g ，2g ，3g 。

（2）求ij g（3）向量~a 参考逆变基~1g ，~2g ，~3g 表示时，~~i i g a a =，求i a 。

（1）[]222~~~~~~~~~3~2~1= +•= +• +×=• ×=k j k k j j i i g g g g+−=+× += ×=~~~~~~~~3~2~121211i j k k j j i g g g g~~~~~~1~3~22211j k i k j g g g g +−= × += ×=~~~~~2~1~32211k j i i g g gg =+×= ×=(2) g ij =gg ii ⋅gg jj �g ij �=�3/4−11/2−12−11/2−11�(3)a i =aa ⋅gg ii a 1=2x,a 2=x +y,a 3=y +z2. 已知笛卡尔坐标系331e e e ,,，一个新的坐标系定义为−−−= ′′′32132161312161312162310e e e e e e 向量321e e e x 321x x x ++=，给定函数2321x x )f(−=x 。

（1） 求函数f 的梯度）（f grad（2） 求向量x 参考新坐标系的表示形式i ′′=e x i x（3） 求函数f 在新的坐标系下的表达形式),,(321′′′′x x x f （4） 判断）（f grad 的客观性。

3. 二维情况下，一质点应力张量σ主值6.11=σλ，3.22=σλ。

主方向2112123e e N −=，2122321e e N +=。

连续介质力学1d

连续介质力学1d

G gi
G g
j
G ...g
k
G g
l
=
T ...kl ij...
G g
i
G g
j
G ...gk
G gl
论
张 量 复 习
散 度 旋
右左散 散度 度张量∇TG的⋅⋅T∇G散==度gG∂∂s：xT⋅Gs∂∂x⋅TGgsG
= T s
... ks
ij... ;s
=
∇
sT
sj... ...kl
G g G g
i j
左、右梯度均为n+1阶张量,一般是两个不同的张量
张 量 复
仅对标量场有ϕ∇ = ∇ϕ
G
G
对矢量场有 F∇ = (∇F )T
习
•张量场的微分:
GG GG G
梯
dT = (T∇) ⋅ dx = dx ⋅ (∇T ) (1.102)
度 以上运算均涉及张量场对坐标的偏导数—协变导数
8
—
3)协变导数的G 定义
Γ ij ,l
= Γijk gkl
=
∂g j ∂xi
⋅
G g
k
g
kl
=
∂g j ∂xi
G ⋅ gl
=
∂
2
G x
∂xi∂x j
G ⋅ gl
(1.92)
复 习
∴ Γij,l = Γ ji,l
(1.93)
—
张 量 的
Γ ij ,l
=
1 2
(
∂g ∂x
il j
+
∂g jl ∂xi
−
∂g ij ∂xl
)
(1.94)
第 一 章

连续介质力学课件

连续介质力学课件

第五章 内容提要
7.位移变分法
⑴瑞利－里茨法：设定位移试函数，
u u (x, y) A u (x, y),
0
mm
m
v v (x, y) B v (x, y),
0
mm
预先满足 su上的约束m边界条件，再满足
瑞利－里茨变分方程，
U
Am
U
B m
A fxum d x d y
sσ
f
u
xm
d
s,
(m 1,2)
f v d x d y f v d s.
A ym
sσ y m
第五章 内容提要
⑵伽辽金法：设定位移势函数预先满足su 上的约束边界条件和sσ 上的应力边界
条
件，再满足伽辽金变分方程，
E 2u 1 μ 2u 1 μ 2v
A
[ 1
μ2
E
A
[ 1
μ2
( x2 2v ( y 2
xy
x
f
y
0.
第二章 内容提要
（2）几何方程
x
u x
,
y
v y
,
（3）物理方程
xy
u y
xv.
x
1 E
(σ x
σ y ), y
1 E
(σ y
σx ),
xy
2(1 E
) xy .
第二章 内容提要
和边界条件： （1）应力边界条件
(lσ x m yx )s f x ,
(mσ y l xy )s f y .
（3）若为多连体，还须满足位移单值条件。 当不记体力时，应力分量的表达式为
σ
ρ
1 ρ
Φ ρ

连续介质力学2-1

连续介质力学2-1

§1-2 内蕴导数与物质导数 1. 矢量的内蕴导数 是场方程（ 显函数） 设曲线l：x i = x i (s )。矢量a ( x )是场方程（只是 x显函数） 则a 沿l方向的导数为 dx da ∂a dx i = = ak , i i e k ds ∂x i ds ds
δak dx i 的内蕴导数（内禀、 称 = ak , i 为ak 对s的内蕴导数（内禀、绝 对） δs ds
2. 连续介质的物质描述 XⅢ b(t)是B运动、 是 运动 运动、 变形的结果， 变形的结果， 故点与点之 间一一对应， 间一一对应， 存在映射
B P p
b(t)
E3 O
R
E2
XⅡ
E1
XⅠ
e3
r(t) e2
x k = x k (X , t )
e1
说明1. 说明 此映射的意义 说明2. 说明 此映射不涉及两坐标间的关系
2. 张量的内蕴导数
ˆ dx k dT δTij e i e j = Tij , k ei e j = ds δs ds
3. 矢量的物质导数 设曲线l：x i = x i (s )。矢量a ( x , s )是x和s的显函数 da ∂a = ds ∂s ∂a + ∂x i dx i ∂ak = ds ∂s ∂a k + ∂x i dx i e k ds
∫∫∫ [Q ( x , t + ∆t ) − Q ( x , t )]dΩ Ω
∂Q dΩ = ∫∫∫ ∂t Ω
1 lim ∆t ∆t → 0
∫∫∫ Q ( x , t + ∆t )dΩ
∆Ω
dS S
d 是dS作微小位移时 作微小位移时 扫过的体积，其上的Q值与 扫过的体积，其上的 值与 dS上的值充分接近。 上的值充分接近。 上的值充分接近

第一章 连续体力学

第一章 连续体力学
根据功能原理和连续性方程， 根据功能原理和连续性方程， 功能原理 可以得到伯努利方程如下
1 2 1 2 p1 + ρv1 + ρgh1 = p2 + ρv2 + ρgh2 2 2 1 2 p + ρv + ρgh = 常数 2
b v2 h2
a a′
p 1 S1
v1 h1
b′
适用条件
p 2 S2
黏滞性很小
A 0
RA
2γ p B − p0 = − RB
而 可得
pB = p A + ρgh
2γ 1 1 h= R −R ρg A B
四、毛细现象
水银与玻璃板
水滴与玻璃板
讨论
接触角θ 接触角θ
θ θ
分类(Classify): (1) 分类(Classify):
润湿：固体和液体接触时， 润湿：固体和液体接触时， 它们的接触角为锐角的现 象。 不润湿： 不润湿：固体和液体接触 它们的为钝角的现象。 时，它们的为钝角的现象。
雨后初晴的礼物
1. 表面张力系数的测量( measurement) 表面张力系数的测量( 拉脱法
讨论
F = 2γl
l
液膜与空气有两个接触面
表面张力能的属性： 表面张力能的属性：
F克服表面张力所做的功
F
dW = Fdx = 2γl ⋅ dx = γdS
其中 dS 于是
A
A'
= 2ldx 是液膜表面积的增量
§2
静止液体的性质
重点
静止液体的压强 静止液体的压强 表面张力 拉普拉斯公式 毛细现象
一、液体的压强
∆f 压强的定义： 压强的定义： p = ∆S

第一章绪论

第一章绪论

第一章绪论思考题1．何为粘滞性？它与切应力以及剪切变形速率之间符合何种定律？答：液体一受剪切（尽管切力很小，只要切力存在）就会连续变形（即流动），液体的这种特性称为易流性。

液体在流动（连续不断变形）的过程中，其内部会出现某种力抵抗这一变形。

在流动状态下液体抵抗剪切变形速率能力的度量称为液体的年制性（亦称粘性）。

F = μA du / dy2．试说明为什么可以把液体当作连续介质，这一假说的必要性、合理性以及优越性何在？答：在一般工程问题中所研究的液体空间比分子尺寸远大得多，而且要解决的工程问题是液体大量分子微观运动的物理量统计平均的结果，即宏观特性。

欧拉的连续兼职模型将液体看成是有无数没有微观运动的质点组成的没有空隙的连续体，并且认为表征液体运动的各物理量，例如密度、速度、压强等在空间和时间上都是连续分布和连续变化的。

引入该模型后，不仅可使研究工作大为简化，而且应用以连续函数为基础的数学分析这一强有力的工具。

3．液体内摩擦和固体间的摩擦有何不同性质？答：对于固体，在应力低于比例极限的情况下，切应力与切应变成线性关系（剪切胡克定律），而液体的切应力与切应变率成线性关系。

4．液体和气体产生粘滞性的机理有何不同？答：液体和气体的微观结构不同。

由于液体的分子间距较小，液体的粘性主要取决于液体分子间的相互吸引力，温度越高，液体分子热运动越激烈，分子摆脱互相吸引的能力越强，导致液体的粘度随温度的升高而减小。

气体的粘性主要取决于气体分子间相互碰撞引起的动量交换，温度越高，气体分子间的动量交换越激烈，导致气体的粘度随温度的升高而增大。

5．何为牛顿流体？答：凡事满足牛顿内摩擦定律F = μA du / dy的流体成为牛顿流体。

如空气、水、油和水银。

6．作用于液体上的力有哪几类？它们分别与何种量有关？答：按里的作用范围来分，作用于液体的力可氛围表面力和质量力两类。

表面力是作用在液体的表面或者界面上且与液体或液体与固体的接触面上，故又称为接触力。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
单元体的变形—— 变形几何理论；
单元体受力与变形
间的关系——本构理 论；
建立起普
遍适用的理 论与解法。
1、涉及数学理论较复杂，并以其理论与解法的严 密性和普遍适用性为特点；
2、弹塑性力学的工程解答一般认为是精确的； 3、可对初等力学理论解答的精确度和可靠进行量。
25
弹塑性力学的研究方法
弹塑性力学基本方程的建立方法：
26
七、弹塑性力学的基本理论与解法
1. 弹塑性力学的基本理论框架
弹塑性力学和材料力学都是固体力学的分支 学科，所求解的大多数问题都是超静定问题。因 此，在分析问题研究问题时的最基本思路是相同 的，即对于一个静不定问题的求解，一般都要经 过三个方面的分析，这三个方面分别为：（1）静 力平衡条件分析；（2）几何变形协调条件分析； （3）物理条件分析。从而获得三类基本方程，联 立求解，再满足具体问题的边界条件，即可使静 不定问题得到解决。这三方面的方程汇集于下：
力以及它们与固体、液体及气体 的平衡、变形或 运动的关系。 连续介质力学
连续介质力学（Continuum mechanics）是物 理学（特别的，是力学）当中的一个分支，是处 理包括固体和流体的在内的所谓“连续介质”宏
观 性质的力学。
3
固体：固体不受外力时，具有确定的形状。固体包括不可变形的 刚体 和可变形固体。刚体在 一般力学 中的 刚体力学 研究；连续介 质力学中的 固体力学 则研究可变形固体，在应力，应变等外在因素 作用下的变化规律，主要包括 弹性 和 塑性 问题。
9
二、现代力学的发展及其特点
1、现代力学的发展
材料与对象： 金属、土木石等 新型复合材料、 高分子材料、 结构陶瓷、功能材料。
尺 度：宏观、连续体 含缺陷体，细、微观、 纳米尺度。
实验技术： 电、光测试实验技术 全息、超声、 光纤测量，及实验装置的大型化。
10
应用领域：航空、土木、机械、材料生命、微电 子技术等。
声学
次声学 超声学 电声学 大气声学 音乐声学 语言声学 建筑声学 生理声学 生物声学 水声学
电磁学
磁学 电学 电动力学
量子物理学
量子力学 核物理学 高能物理学 原子物理学 分子物理学
固体物理学
高压物理学 金属物理学 表面物理学
5
1、学科分类
按运动与否分：
静力学：研究力系或物体的平衡问题，不涉及 物体运动状态的改变；如飞机停在地 面或巡航。
在金属塑性加工中，如冲压、锻造、挤压等塑性成形 过程，将工艺现象提升到理论阶段，进一步指导实践。
（塑性变形很大，弹性变形可以忽略）
17
四、弹塑性力学发展简介
1678年，Hooke：变形和外力成正比。 1820~1830年，Navier、Cauahy、Saint Venant：应力、
应变的概念，变形体的平衡方程、几何方程、协调方 程、广义虎克定律；------弹性力学的理论基础。 1773年，Coulomb：土的屈服条件。 1864年，Tresca：最大剪应力屈服条件。 1871年，Levy：三维塑性应力--应变关系。 1913年，Mises：形变能屈服条件。 1930年，Prandtl，Reuss：增量理论。 1943年，Hencky，Nadai，Iliushin：形变理论。 1950年~，塑性位势理论、有限单元法
11
● 引进新的科学技术成果， 内容更加丰富：
◆ 新材料－复合材料、聚合物等； ◆ 新概念－失效、寿命等； ◆ 新理论－损伤、混沌等； ◆ 新方法－数值方法、工程力学建模方法。
12
2﹒现代力学的特点
● 与计算机应用相结合， 与其他基础或技术学科相互结合与渗透。
计算机应用：计算力学+计算机应用解决复杂、 (60年代) 困难的工程实际问题。
27
(1)．平衡（或运动方程）：
ij ' j Fi 0
(2)、几何方程：
ij

1 2
(ui' j
u j 'i )
(3)．本构方程（物性方程）
（A）在弹性变形阶段，
ij

1
E
ij


E
ij
ii
（B）在弹塑性变形阶段，屈服函数 f ( ij ) 0 则有：
sij ，d m
3Kd m
（i i）Levy-Mises
( 1 )
2
（a）理想刚塑性材料 。
性、断裂等力学问题，奠定必要的理论基础。
16
（1）工程结构和机械零件的设计
物体达到塑性阶段时，并没有破坏，它还有能力继续 工作，可把构件设计到部分塑性、部分保持弹性状态， 更合理地确定工程结构和机械零件的安全系数，节省材 料。（不允许大变形，塑性变形限制在弹性变形的量级）
（2）指导金属塑性加工
生物力学： (70年代冯元祯博士) 生物材料力学性能、微循环、定量生理学、心血管系 统临床问题和生物医学工程等。 “没有生物力学，就不能很好地了解生理学。”
14
二、 弹塑性力学的研究对象
在研究对象上，材料力学的研究对象是固 体，且基本上是各种杆件，即所谓一维构件。
弹塑性力学研究对象也是固体，是不受 几何尺寸与形态限制的能适应各种工程技术 问题需求的物体。
运动学：研究物体如何运动，不讨论运动与受 力的关系；如飞行轨迹、速度、加速度。
动力学：研究力与运动的关系。 如何提供加速度？
6
● 按研究对象分：
◆ 一般力学： 研究对象是刚体。研究力及其与
运动的关系。分支学科有理论力学，分析力学等。
◆ 固体力学：研究对象是可变形固体。研究材料
变形、流动和断裂时的力学响应。其分支学科有： 材料力学、结构力学、弹性力学、 塑性力学、 弹塑性力学、断裂力学、流变学、疲劳等。
变形前，在某表 面绘制标志线； 变形后，观察总 结构件表面变形 的规律。
做出平截面 假设，经三 方面分析， 解决问题。
a、研究方法较简单粗糙； b、涉及数学理论较简单； c、材料力学的工程解答一般为近似解。
24
◆ 弹塑性力学研究问题的基本方法
以受力物 体内某一 点（单元 体）为研 究对象
单元体的受力—— 应力理论；
19
1、物理假设:
（1）连续性假设：假定物质充满了物体所占有的全部 空间，不留下任何空隙。
（2）均匀性与各向同性的假设：假定物体内部各点处， 以及每一点处各个方向上的物理性质相同。
（3）力学模型的简化假设： （A）完全弹性假设 ；（B）弹塑性假设。
20
2、几何假设——小变形条件
假定物体在受力以后，体内的位移和变形是微小的 ，即体内各点位移都远远小于物体的原始尺寸，而且应变 ( 包括线应变与角应变 )均远远小于1。根据这一假定： （1）在弹塑性体产生变形后建立平衡方程时，可以
塑性 ：应力作用后，不能恢复到原来的形状，发生永久形变。 弹性 ：应力作用后，可恢复到原来的形状。 流体 ：流体包括 液体 和 气体 ，无确定形状，可流动。流体最重 要的性质是 粘性 （viscosity，流体对由剪切力引起的形状的抵抗 力，无粘性的 理想气体 ，不属于流体力学的研究范围）。从理论研 究的角度，流体常被分为 牛顿流体 和 非牛顿流体 牛顿流体 ：满足 牛顿粘性定律 的流体，比如水和空气。 非牛顿流体 ：不满足 牛顿粘性定律 的流体，介乎于固体和牛顿 流体之间砄物质形态。
设计准则：静强度、 断裂控制设计、抗疲劳设 计、、刚度设计 损伤容限设计、结构优化 设计、耐久性设计和可靠性设计等。
设计目标：保证结构与构件的安全和功能 设计——制造——使用——维护的综合性分析 与控制，功能——安全——经济的综合性评价， 自感知、自激励、自适应（甚至自诊断、自修复） 的智能结构。
(3) 力与变形间的本构关系 (物理分析)
固体材料受力作用必然产生相应的变形。不同的材料，不 同的变形，就有相应不同的物理关系。则对一点单元体的受力 与变形间的关系进行分析，应满足的条件是什么？（物理条件 ，也即本构方程。）
23
2、弹塑性力学研究问题的基本方法
◆ 材料力学研究问题的基本方法：
选一维 构件整 体为研 究对象
4
物理学分支巡礼 物理学概览
力学
静力学 动力学 流体力学 分析力学 运动学 固体力学 材料力学 复合材料力学 流变学 结构力学 弹性力学 塑性力学 爆炸力学 磁流体力学 空气动力学 理性力学 物理力学 天体力学 生物力学 计算力学
热学 热力学
光学
几何光学 波动光学 大气光学 海洋光学 量子光学 光谱学 生理光学 电子光学 集成光学 空间光学
造成两者间这种差异的根本原因是什么呢？
15
三、 弹塑性力学的基本任务
可归纳为以下几点： 1．建立求解固体的应力、应变和位移分布规律的
基本方程和理论； 2．给出初等理论无法求解的问题的理论和方法，
以及对初等理论可靠性与精确度的度量； 3．确定和充分发挥一般工程结构物的承载能力，
提高经济效益； 4．为进一步研究工程结构物的强度、振动、稳定
22
(1) 受力分析及静力平衡条件 (力的分析)
对一点单元体的受力进行分析。若物体受力作用，处于 平衡状态，则应当满足的条件是什么？（静力平衡条件）
(2) 变形分析及几何相容条件 (几何分析)
材料是连续的，物体在受力变形后仍应是连续的。固体 内既不产生“裂隙”，也不产生“重叠”。则材料变形时， 对一点单元体的变形进行分析，应满足的条件是什么？（几 何相容条件）
几何学：位移与应变的关系--变形协调关系（几何方程和位移边界
条件）。
静力学：物体的平衡条件--平衡微分方程和应力边界条件。 物理学：应力与应变（或应变增量）的关系--本构关系。
求解弹塑性力学问题的数学方法：