下载文档原格式
一、劳动定额定期修改1、压缩率：是指对工时定额水平的调整幅度。
压缩率=（原产品台份定额-计划产品台份定额）/原产品台份定额*100%例：某产品原台份的工时定额为100小时，计划调整到80小时，求压缩率。
压缩率=（100-80）/100*100%=20%2、修改劳动定额的简易方法1/零部件的实耗工时=修改前的定额工时/（1+平均超额的百分比）2/平均超额的百分比=实际完成定额工时数/应出勤工时数—13/修改后新的单件工时定额=（1+允许超额幅度）*零部件的实耗工时例：某企业甲车间生产产品A，2011年工时定额a为136工时/吨，生产员工人数为20人，年实际产量为426吨，年制度工日为251天，平均出勤率95%，2012年修改后的定额工时允许比上一年实际耗用工时高20%（k允许超额幅度），试核算出新的工时定额。
1/零部件的实耗工时=修改前的定额工时/（1+平均超额的百分比）89.56=136/（1+0.5186）2/平均超额的百分比=实际完成定额工时数/应出勤工时数—10.5186 =426*136/251*8*20*0.95-13/修改后新的单件工时定额=（1+允许超额幅度）*零部件的实耗工时107.47=（1+20%）*89.56压缩率=（136-107.47）/136*100%=20.98%3、劳动定额完成程度指标的计算方法（1）按产量定额计算产量定额完成程度指标=单位时间内实际完成的合格产品产量/产量定额*100%（2）按工时定额计算（实行多种产品只能用工时定额计算）工时定额完成程度指标=单位产品的工时定额/单位产品的实耗工时*100%例：某月甲车工完成合格产品720件，实耗工时为160，并知该产品车削加工产量定额为3件/工时。
试计算该车工劳动定额完成情况。
（1）产量定额完成程度指标=单位时间内实际完成的合格产品产量/产量定额*100%150%=720/（3*160）*100%（2）工时定额完成程度指标=单位产品的工时定额/单位产品的实耗工时*100%150% =（720/3）/160*100%（3）在生产多种产品的情况下只能采用工时定额的形式劳动定额完成程度指标=完成定额工时总数/实耗工时总数=∑某产品的实际产量（Q1）*某单位产品的工时定额（t n）/∑某产品的实际产量（Q1）*某单位产品的实耗工时（t1）例：某车间在报告期内生产甲、乙、丙三种产品，每种产品的劳动定额完成情况如下表。
匈牙利法解决人数与任务数不等的指派问题于凯重庆科技学院经济管理学院物流专业重庆沙坪坝区摘要：本文将讨论运筹学中的指派问题，而且属于非标准指派问题，即人数与任务数不相等的指派问题，应当视为一个多目标决策问题，首先要求指派给个人任务数目两两之间相差不能超过1,其次要求所需总时间最少，并且给岀了该类问题的求解方法。
关键词：运筹学指派问题匈牙利算法系数矩阵解矩阵引言：在日常的生产生活中常遇到这样的问题：有n项任务，有n个人员可以去承担这n 项任务，但由于每位人员的特点与专长不同，各对象完成各项任务所用的时间费用或效益不同：有因任务性质要求和管理上需要等原因，每项任务只能由一个人员承担来完成，这就涉及到应该指派哪个人员去完成哪项任务，才能使完成n项任务花费总时间最短,总费用最少, 产生的总效益最佳。
我们把这类最优匹配问题称为指派问题或分配问题。
1. 指派问题的解法——匈牙利法早在1955年库恩（w.w.ku.hn）就提出了指派问题的解法，该方法是以匈牙利数学家康尼格（koning）提岀的一个关于矩阵中0元素的定理为基础，因此得爼匈牙利法（The Hungonrian Method of Assignment）1.1匈牙利解法的基本原理和解题思路直观的讲，求指派问题的最优方案就是要在n阶系数矩阵中找出n个分布于不用行不同列的元素使得他们的和最小。
而指派问题的最优解又有这样的性质：若从系数矩阵C （ij）的一行（列）各元素都减去该行（列）的最小元素，得到新矩阵CB （ij）,那么以CB （ij）为系数矩阵求得的最优解和原系数矩阵C （ij）求得的最优解相同。
由于经过初等变换得到的新矩阵CB （ij）中每行（列）的最小元素均为"O”，因此求原指派问题C （ij）的最优方案就等于在新矩阵CB （ij）中找出n个分布于不同行不同列的"O”元素（简称为“独立O元素”），这些独立O元素就是CB （ij）的最优解，同时与其对应的原系数矩阵的最优解。
匈牙利法则例题匈牙利法则是一种用来解决数学问题的启发式方法。
它的核心思想是将问题分解成更小的部分，然后逐步解决这些部分，最终得出整体的解决方案。
这种方法在解决复杂的数学问题时非常有用，因为它可以帮助人们更好地理解问题的本质，并找到解决方案的线索。
让我们通过一个具体的例题来了解匈牙利法则的应用。
假设有一个旅行商需要从城市A出发，依次经过城市B、城市C、城市D和城市E，最后回到城市A。
每两个城市之间都有一定的距离，旅行商的目标是找到一条路径，使得他的总行程最短。
这个问题可以用图论中的最短路径算法来解决，但我们也可以用匈牙利法则来思考一下。
首先，我们可以将整个旅行路径分解成几个小的部分，比如从A到B、从B到C、从C到D、从D到E，最后从E回到A。
然后，我们可以分别计算出每段路径的长度，并找到每段路径的最短路径。
最后，将这些最短路径连接起来，就得到了整个旅行商的最短路径。
通过这个例题，我们可以看到匈牙利法则的应用。
它通过将复杂的问题分解成更小的部分，然后逐步解决这些部分，最终得出整体的解决方案。
这种方法不仅可以帮助人们更好地理解问题的本质，还可以帮助他们找到解决问题的线索。
除了数学问题，匈牙利法则在其他领域也有广泛的应用。
比如，在计算机科学中，匈牙利法则常常用来解决图论、网络流等问题；在管理学中，匈牙利法则可以帮助人们更好地分析和解决复杂的管理问题。
总的来说，匈牙利法则是一种非常有用的启发式方法，它可以帮助人们更好地理解和解决各种复杂的问题。
在实际应用中，我们可以通过以下步骤来应用匈牙利法则解决问题：1. 将复杂的问题分解成更小的部分；2. 逐步解决这些小部分，找到它们的解决方案；3. 将这些解决方案连接起来，得出整体的解决方案。
通过这种方法，我们可以更好地理解和解决各种复杂的问题，不仅可以提高解决问题的效率，还可以帮助人们更好地理解问题的本质。
因此，匈牙利法则在数学、计算机科学、管理学等领域都有着广泛的应用前景。
全国人力资源管理师答题技巧与思路拓展人力资源管理师考试是中国人力资源协会认可的专业资格认证考试，考试内容涵盖了人力资源管理的各个领域。
在备考过程中，熟悉答题技巧并拓展思路非常重要。
本文将为大家介绍全国人力资源管理师答题技巧以及如何拓展思路，希望对大家的备考有所帮助。
一、选择题的技巧1. 留意关键词选择题通常会在题干中隐藏一些关键词，通过留意这些关键词可以快速找到答案。
例如，“以下哪项不属于人力资源管理的职责？”关键词是“不属于”，答案很可能在选项中。
2. 排除法当你对某个选项有疑虑时，可以尝试使用排除法。
通过分析其他选项，找出错误的选项，并逐个排除，可以提高正确选出答案的几率。
3. 注意细节选择题往往会设立干扰项，需要注意题目的细节。
特别是数字、时间、比例等具体数据，一定要仔细核对，在计算时避免疏忽。
二、案例分析题的技巧1. 理清思路案例分析题通常会给出一个实际情境，要求你依据这个情境进行分析和解决问题。
在阅读案例时，要理清思路，明确问题的关键点和要解决的核心。
2. 简明扼要在回答案例分析题时，要注意简洁明了。
避免啰嗦冗长，直接回答问题即可。
将答案按照逻辑顺序组织，附上合适的理论知识支撑，可以提高答案的质量。
3. 多角度思考案例分析题往往需要从多个角度进行思考和分析。
不仅要考虑人力资源管理的角度，还要考虑企业战略、法律法规、人际关系等方面的影响。
在回答过程中，可以尝试从多个角度进行论述，展示自己全面深入的思考能力。
三、论述题的技巧1. 理论联系实际在论述题中，要能够将理论知识与实际案例相结合，展示你对人力资源管理问题的洞察力和应用能力。
可以引用真实的案例或自己的经验，说明理论在实践中的运用和解决问题的效果。
2. 结构清晰论述题需要有明确的结构，分清主次，条理清晰。
可以采用提出观点、论证观点、总结观点的结构，确保逻辑连贯，使读者容易理解你的思路和论证过程。
3. 深入发掘在论述题中，要尽量深入发掘问题，提供有实质性的思考和建议。
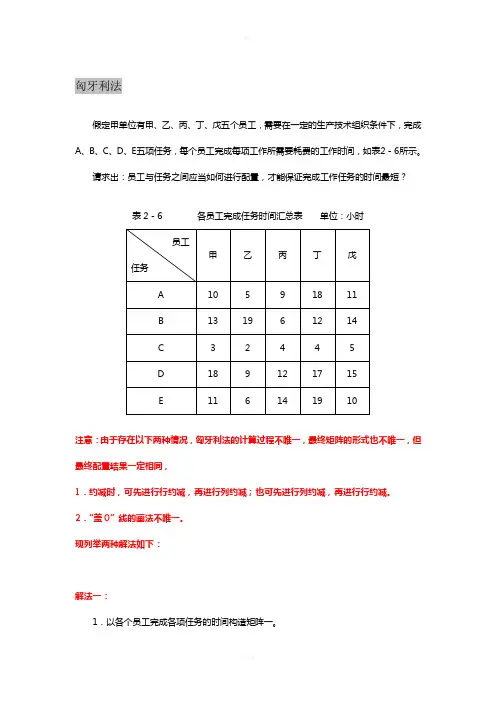
匈牙利法
假定甲单位有甲、乙、丙、丁、戊五个员工，需要在一定的生产技术组织条件下，完成A、B、C、D、E五项任务，每个员工完成每项工作所需要耗费的工作时间，如表2－6所示。
请求出：员工与任务之间应当如何进行配置，才能保证完成工作任务的时间最短？
表2－6 各员工完成任务时间汇总表单位：小时
注意：由于存在以下两种情况，匈牙利法的计算过程不唯一，最终矩阵的形式也不唯一，但最终配置结果一定相同，
1．约减时，可先进行行约减，再进行列约减；也可先进行列约减，再进行行约减。
2．“盖0”线的画法不唯一。
现列举两种解法如下：
解法一：
1．以各个员工完成各项任务的时间构造矩阵一。
表2－7矩阵一
10 5 9 18 11
13 19 6 12 14
3 2
4 4 5
18 9 12 17 15
11 6 14 19 10
2．对矩阵一进行行约减，即每一行数据减去本行数据中的最小数，得矩阵二。
表2－8 矩阵二
5 0 4 13 6
7 13 0 6 8
1 0
2 2 3
9 0 3 8 6
5 0 8 13 4
3．检查矩阵二，若矩阵二各行各列均有“0”，则跳过此步，否则进行列约减，即每一列数据减去本列数据中的最小数，得矩阵三。
表2－9 矩阵三
4 0 4 11 3
6 13 0 4 5
0 0 2 0 0
8 0 3 6 3
4 0 8 11 1
4．画“盖0”线。
即画最少的线将矩阵三中的0全部覆盖住，得图2－5。
图2－5 矩阵四
操作技巧：从含“0”最多的行或列开始画“盖0”线。
5．数据转换。
若“盖0”线的数目等于矩阵的维数则跳过此步，若“盖0”线得数目小于矩阵得维数则进行数据转换，本例属于后一种情况，应进行转换，操作步骤如下：
（1）找出未被“盖0”线覆盖的数中的最小值λ，例中λ＝1。
（2）将未被“盖0”线覆盖住的数减去λ。
（3）将“盖0”线交叉点的数加上λ。
本例结果见表2－10 矩阵五。
表2－10 矩阵五
3 0
4 10 2
5 13 0 3 4
0 1 3 0 0
7 0 3 5 2
3 0 8 10 0
6．重复4步和5步（计算过程见矩阵五a和矩阵五b），直到“盖0”线的数目等于矩阵的维数。
本例最终矩阵见表2－11。
矩阵五a
矩阵五b
表2－11 矩阵六
0 0 4 7 2
2 1
3 0 0 4
0 4 6 0 3
4 0 3 2 2
0 0 8 7 0
7．求最优解。
对n维矩阵，找出不同行、不同列的n个“0”，每个“0”的位置代表一对配置关系，具体步骤如下：
（1）先找只含有一个“0”的行（或列），将该行（或列）中的“0”打“√”。
（2）将带“√”的“0”所在列（或行）中的“0”打“⨯”。
（3）重复（1）步和（2）步至结束。
若所有行列均含有多个“0”，则从“0”的数目最少的行或列中任选一个“0”打“√”。
其结果如表2－12矩阵七所示，即员工甲负责任务A，员工乙负责任务D，员工丙负责任务B，员工丁负责任务C，员工戊负责任务E，参照表2－6各员工完成任务时间汇总表，得出表2－13所示的员工配置最终结果。
表2－12 矩阵七
0 √0 ⨯ 4 7 2
2 1
3 0 √0 ⨯ 4
0 ⨯ 4 6 0 √3⨯
4 0 √ 3 2 2
0 ⨯0 ⨯8 7 0 √
表2－13 员工配置最终结果单位：小时
解法二：
1．以各个员工完成各项任务的时间构造矩阵一。
表2－7矩阵一
10 5 9 18 11
13 19 6 12 14
3 2
4 4 5
18 9 12 17 15
11 6 14 19 10
2．对矩阵一进行行约减，即每一行数据减去本行数据中的最小数，得矩阵二。
表2－8 矩阵二
5 0 4 13 6
7 13 0 6 8
1 0
2 2 3
9 0 3 8 6
5 0 8 13 4
3．检查矩阵二，若矩阵二各行各列均有“0”，则跳过此步，否则进行列约减，即每一列数据减去本列数据中的最小数，得矩阵三。
表2－9 矩阵三
4 0 4 11 3
6 13 0 4 5
0 0 2 0 0
8 0 3 6 3
4 0 8 11 1
4．画“盖0”线。
即画最少的线将矩阵三中的0全部覆盖住，得图2－5。
图2－5 矩阵四
操作技巧：从含“0”最多的行或列开始画“盖0”线。
5．数据转换。
若“盖0”线的数目等于矩阵的维数则跳过此步，若“盖0”线得数目小于矩阵得维数则进行数据转换，本例属于后一种情况，应进行转换，操作步骤如下：
（1）找出未被“盖0”线覆盖的数中的最小值λ，例中λ＝1。
（2）将未被“盖0”线覆盖住的数减去λ。
（3）将“盖0”线交叉点的数加上λ。
本例结果见表2－10 矩阵五。
表2－10 矩阵五
3 0
4 10 2
5 13 0 3 4
0 1 3 0 0
7 0 3 5 2
3 0 8 10 0
6．重复4步和5步（计算过程见矩阵五a和矩阵五b），直到“盖0”线的数目等于矩阵的维数。
本例最终矩阵见表2－11。
矩阵五a
0 0 1 7 2
5 1
6 0 3 7
0 4 3 0 3
4 0 0 2 2
0 0 5 7 0
矩阵五b
表2－11 矩阵六
0 0 1 7 2
5 1
6 0 3 7
0 4 3 0 3
4 0 0 2 2
0 0 5 7 0
7．求最优解。
对n维矩阵，找出不同行、不同列的n个“0”，每个“0”的位置代表一对配置关系，具体步骤如下：
（1）先找只含有一个“0”的行（或列），将该行（或列）中的“0”打“√”。
（2）将带“√”的“0”所在列（或行）中的“0”打“⨯”。
（3）重复（1）步和（2）步至结束。
若所有行列均含有多个“0”，则从“0”的数目最少的行或列中任选一个“0”打“√”。
其结果如表2－12矩阵七所示，即员工甲负责任务A，员工乙负责任务D，员工丙负责任务B，员工丁负责任务C，员工戊负责任务E，参照表2－6各员工完成任务时间汇总表，得出表2－13所示的员工配置最终结果。
表2－12 矩阵七
0√0 1 7 2
5 1
6 0√ 3 7
0 ⨯ 4 3 0 √ 3
4 0√0 ⨯ 2 2
0 ⨯0 ⨯ 5 7 0√。
