高等数学(2017高教五版)课件格林公式·曲线积分与路线的无关性(工科类)资料
- 格式:ppt
- 大小:2.20 MB
- 文档页数:3




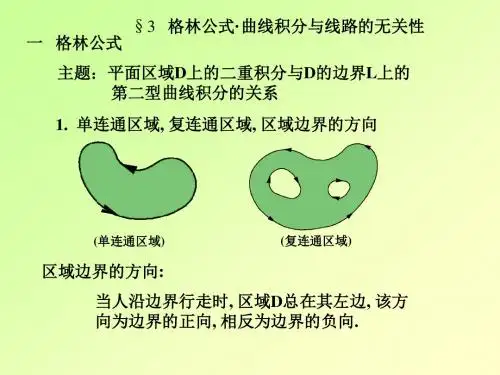






第十七章 各类积分的联系回顾:一元函数积分学:)()()('a F b F dx x F ba -=⎰§17-1 格林公式及曲线积分与路径无关的条件一、格林公式概念:单连通区域, 复连通区域; 正向;格林定理:设闭区域2R D ⊂,是由有限多条分段光滑的闭曲线Γ所围成. 函数),(),,(y x Q y x P 在D 上具连续的一阶偏导,则有 σd yPx Q Qdy Pdx D)(∂∂-∂∂=+⎰⎰⎰Γ(格林公式) 其中Γ是取正向记: 图示 光设D(既是X 型又是Y 型)即穿过区域D 内部且平行于坐标轴的直线与D 的边办曲Γ的交点恰两点.设D:b x a ≤≤, )()(21x y x ϕϕ≤≤()()[]dx x x P x x P dy y y x P dx dxdy y Pb a b a x x D⎰⎰⎰⎰⎰-=∂∂=∂∂)(,)(,),(12)()(21ϕϕϕϕ ()()()()[]dxx x P x x P dx x x P dx x x P Pdx Pdx Pdx baa bb a⎰⎰⎰⎰⎰⎰-=+=+=ΓΓΓ)(,)(,)(,)(,212112ϕϕϕϕ 因此 ⎰⎰⎰Γ=∂∂-Pdx dxdy yPD设D:d y c ≤≤ )(2)(1y y x ϕϕ≤≤ 类似可证 ⎰⎰⎰Γ=∂∂DQdy dxdy xQ即得格林公式例1:计算曲线积分ydx x dy xy 22-⎰ΓΓ:(1)222a y x =+ 逆时针(2)222a y x =+ 上半部分,x 轴,逆 解:y x P 2-= 2xy Q +=2x y P -=∂∂ 2y xQ=∂∂ 由Green 公式 (1)u a dr r d d x y ydx x dy xy aD-=⋅=+=-⎰⎰⎰⎰⎰Γ420322222)(πθσπ计算曲线积分(2)403022224)(a dr r d d x y ydx x dy xy aDπθσπ==+=-⎰⎰⎰⎰⎰Γ例2:计算椭圆12222=+by a x 所围面积A.解: Γ:常数方程 t a x cos = t b y sin = []ab dt t a t b t b t a ydx xdy A ππ=-⋅-⋅=-=⎰⎰Γ20)sin (sin cos cos 2121 例3:计算⎰Γ+-=22y x ydxxdy I ,其中Γ是(1)使所含区域D 不含原点的分段光滑封闭曲线,沿正向(2) 含原点但不径原点解:22y x y P +-= 22y x x Q += 22222)(y x x y y p x +-=∂∂=∂∂θ (1) 满足Green Th 连续条件 ⎰⎰⎰==+-=ΓDd y x ydxxdy I 0022σ(2) 不满足Green Th 连续条件选取适当小的0>ε,作圆周 :222ε=+y x (使 全部含于Γ所围区域) 记 +Γ围成D, 于是在1D 内, 格林公式成立 ⎰⎰⎰⎰⎰⎰⎰-++ΓΓΓ=-=+==001D d σ 故⎰⎰+-=+-Γ 2222y x ydxxdy y x ydx xdy 法一:右式πθθθθεθεπ2)sin (cos 2sin ,cos 202=+==========⎰d y x 学数方程法二:右式⎰⎰⎰≤+=⋅==-=222221122επσεεy x G d ydx xdy公式二、平面上单边通区域内曲线积分与路径无关的等价条件概念:曲线积分⎰Γ+Qdy Qdx 与路径无关:⎰⎰ΓΓ+=+12Qdy Pdx Qdy Pdx图示 (且公与B A y y ,有关)定理:),(),,(y x Q y x P 和平面单连通域D 上具连续一阶偏导,则如下四条件等价. (1)xQ y P ∂∂=∂∂ D y x ∈),( (2)⎰Γ=+0Qdy Pdx D ∈Γ 分段光滑闭曲线(3)积分⎰Γ+ABQdy Pdx 在D 内与路径Γ无关,公与A,B 位置有关(4)存在单值函数),(y x u u =, D y x ∈),( 使它全微分 Qdy Pdx dy y u dx x u du +=∂∂+∂∂=即P xu =∂∂ Q y u =∂∂ 证明:同证)2()1(⇔, )3()2(⇔ 下证)1()4(⇒, )4()3(⇒, )1()4(⇒ 存在函数),(y x u 使 dy y x Q dx y x P du ),(),(+= 则),(y x P xu=∂∂ ),(y x Q y u =∂∂ 于是 y P y x u ∂∂=∂∂∂2 x Qx y u ∂∂=∂∂∂2 由条件 xy uy x u ∂∂∂=∂∂∂22 (连续) 故xQ y P ∂∂=∂∂ )4()3(⇒曲线积分⎰Γ+ABQdy Pdx 仅与 ),(00y x A ,),(y x B 有关, 记⎰+=),(),(00),(y x B y x A Qdy Pdx y x u (说明右式是y x ,函数)下证 P xu=∂∂ Q y u =∂∂xy x u y x x u x u x ∆-∆+=∂∂→∆),(),(lim 0 xQdyPdx Qdy Pdx y x x y x y x y x x ∆+-+=⎰⎰∆+→∆),(),(),(),(00000limxdxy x P x QdyPdx xx xx y x x y x x ∆=∆+=⎰⎰∆+→∆∆+→∆),(lim lim0),(),(0),(),(lim ),(lim 1y x P y P xxy P x x Th 连续中值===∆∆===→→∆ξξξ⎥⎦⎤⎢⎣⎡=∆+=∆∆∆+===→∆→∆≤≤),(),(lim ),(lim0010y x P y x x P x x y x x P x x θθθ 同理,),(y x Q yu=∂∂ 故 Qdy Pdx dy yu dx x u du +=∂∂+∂∂=推出公式: 图示 CB AC AB +=⋂AC:0y y = 10x x x ≤≤ 0=dy CB:1x x = 10y y y ≤≤ 0=dx 曲线积分计算公式dy y x Q dx y x P Qdy Pdx Qdy Pdx y y y x B y x A x x AB),(),(11100121),(),(0⎰⎰⎰⎰+=+∆+Γ原函数计算公式C dy y y Q dx y x P C Qdy Pdx y x u yy y x y x xx Th ++=++===⎰⎰⎰),(),(),(00000),(),(0过程特D ∈)0,0( ⎰⎰++=x y C dy y x Q dx x P y x u 0),()0,(),( 可证 ),(),(),(0011),(),(1100y x u y x u y x u Qdy Pdx Qdy Pdx ABy x B y x A B A -==+=+⎰⎰Γ------曲线积分的N-2公式 例4:计算dy x xydx OA⎰Γ+22 三路径.解: 图示 xy y x P 2),(= 2),(x y x Q =xQ x y P ∂∂==∂∂2 11)002(2212102)1,1()0,0(22=+⋅+⋅=+=+⎰⎰⎰⎰Γdy x dx x dy x xydx dy x xydx OA例5:计算dy y x x y dx x y y x I )sin sin 2()cos cos 2(22-++=⎰Γ.Γ是1)1(22=+-y x 的上半圆周.从)0,0(O 到)0,2(A解:xQ y P ∂∂=∂∂.I 值与路径无关0=⋅→y OA 0=O x 1=A x ,0=dy则⎰⎰===→242xdx I OA⎰Γ-=-=2I例6:dy x y x x y dx x y y x I )sin sin 2()cos cos 2(221+-++=⎰Γ.Γ:例5. 解一:xQ y P ∂∂+∂∂:不能用与路径无关的相关公式. Γ非闭 :才能用Green 公式.原始方法(第二类曲线积分) 图示 ⎩⎨⎧=+=t y t x sin 1cos 几乎不可能解二:(设法满足二之一: Γ闭)x y y x y P cos 2sin 2+-=∂∂,1sin 2cos 2+-=∂∂y x x y xQ 设1Γ:(从A 到O 直线段)0,0,1,0====dy x x y O A ,则1Γ+Γ构成闭曲线,顺进针.1Γ+Γ所围闭域D:πθ≤≤0, θcos 20≤≤r由Green 公式2)(1πσσ-=-=∂∂-∂∂-=⎰⎰⎰⎰⎰Γ+ΓD Dd d y P x Q (即⎰⎰ΓΓ-=+12π)而dy x y x x y dx x y y x )sin sin 2()cos cos 2(221+-++⎰Γ⎰-==0242xdx故⎰⎰ΓΓ-=--==12421ππI .解三:(设法满足二之另一,xQy P ∂∂=∂∂) .cos cos 22x y y x P += 设y x x y Q sin sin 221-= x Q =221Q Q Q +=则xQ y P ∂∂=∂∂1dy Q Pdx ⎰Γ+1与路径无关.dy Q dy Q Pdx I ⎰⎰ΓΓ++=2111⎰⎰⋅++=2cos )cos 1(2πtdt t xdx24π-=例7:(得用曲线积分求)dy y xy x dx y xy x )2()2(2222--+-+的原函数),(y x u . 并求⎰)2,2()0,1(.(其中Γ是从A(1,0)到B(2,2)的曲线段)解:222y xy x P -+= 222y xy x Q --= y x xQ y P 22-=∂∂=∂∂ C dy y xy x dx y xy x y x u y x +--+-+=⎰)2()2(),(222),()0,0(2C y xy y x x C dy y xy x dx x yx+--+=+--+=⎰⎰3223202023131)2(31),()2()2()2,2()0,1(222)2,2()0,1(2-==--+-+⎰y x u dy y xy x dx y xy x作业: 151P 1(1)(4) 2(已提示) 4(1) 5(2) 6(2)。