高等数学 格林公式
- 格式:ppt
- 大小:3.11 MB
- 文档页数:49

叙述格林公式格林公式是高等数学中的一个重要公式,它在向量场的线积分和面积分之间建立了一种联系。
咱们先来说说格林公式到底是啥。
简单来讲,格林公式就像是一座桥梁,把沿着封闭曲线的线积分和在曲线所围成区域上的面积分给连起来啦。
比如说,有一个封闭曲线围成的区域,咱们想知道沿着这个曲线的某种向量场的线积分,这时候格林公式就能派上用场,通过计算相关的面积分来得出线积分的值。
我给您讲个事儿啊,就前几天我给学生上课的时候,讲到格林公式这部分内容。
有个学生特别较真儿,一直问我为啥这个公式会这样,怎么就能从线积分跳到面积分啦。
我就给他举了个特别形象的例子,我说:“你看啊,咱们把这个封闭曲线想象成一个农场的篱笆,篱笆里面是一块地。
线积分呢,就好比你沿着这个篱笆走一圈,看看走得多累。
而面积分呢,就像是算这块地里能种多少庄稼。
这两者之间是有关系的,格林公式就是告诉咱们怎么从算种庄稼的事儿,知道沿着篱笆走的情况。
”这学生听了,眼睛一下子亮了,好像是明白了点啥。
那格林公式到底有啥用呢?它的用处可大了去啦!比如说在物理学中,计算电场或者磁场的相关问题时,经常会用到格林公式。
还有在工程领域,像流体力学里,研究液体或者气体的流动,格林公式也能发挥重要作用。
要想熟练运用格林公式,可得把相关的概念搞清楚。
比如说啥是曲线的正向,啥是偏导数,这些都是基础中的基础。
可别小看这些基础概念,一旦弄混了,那用格林公式的时候可就容易出错啦。
咱们再来说说怎么证明格林公式。
这证明过程啊,可需要一些数学功底。
得用到一些微积分的知识,像是二重积分的换元法,还有一些巧妙的构造。
不过别担心,只要跟着教材一步一步来,多做几道练习题,慢慢就能理解其中的奥妙啦。
在实际解题的时候,用格林公式得小心一些细节。
比如说曲线是不是封闭的,如果不是封闭的,得想办法给它补成封闭的。
还有曲线是不是光滑的,如果不光滑,可能就得分段计算。
总之啊,格林公式虽然看起来有点复杂,但只要咱们认真学,多练习,就一定能掌握它,让它成为咱们解决数学问题的有力工具。


高数考研备战格林公式的应用与解题技巧格林公式(Green's theorem)是高等数学中的一个重要定理,也是考研数学中的重要内容之一。
它在很多场景中有广泛的应用,帮助我们解决各种复杂的问题。
本文将介绍格林公式的基本原理和应用,并提供一些解题技巧,以帮助考生备战高等数学考研。
一、格林公式的基本原理格林公式是由英国数学家格林(George Green)于1828年提出的,它将二维平面上的曲线积分转化为对该曲线所围成的区域的面积积分。
具体地说,设曲线C是一条分段光滑的闭合曲线,曲线C所包围的区域称为D。
如果函数P(x, y)和Q(x, y)在区域D上具有一阶连续偏导数,那么有格林公式的表达式如下:∮C (Pdx + Qdy) = ∬D (Qₓ - Pᵧ)dA其中,∮C表示曲线C上的曲线积分,∬D表示对区域D上的面积积分,Pdx + Qdy表示关于x和y的微分形式,Qₓ和Pᵧ分别表示Q对x求偏导和P对y求偏导。
二、格林公式的应用格林公式在物理、工程和数学等多个领域都有广泛的应用。
下面将介绍几种常见情况下的应用。
1. 曲线积分的计算格林公式可以帮助我们计算曲线C上的曲线积分。
具体操作是,将积分转化为对曲线所包围的区域D上面积积分的计算。
通过求解二重积分,我们可以更简单地计算出原本复杂的曲线积分。
2. 面积的计算格林公式可以通过计算面积积分来帮助我们计算区域D的面积。
通过求解面积积分,我们可以不需要遍历整个区域来计算面积,而是通过对边界曲线上的积分来得到结果。
这在实际问题中十分有用,节省了计算的时间和精力。
3. 流量的计算格林公式还可以用于计算流体力学中的流量。
通过设定P和Q的形式并代入格林公式,我们可以将流量计算问题转化为对面积积分的计算。
这样一来,我们可以更加方便地求解流体力学中的流量问题。
三、解题技巧在考研中遇到格林公式的应用题时,我们可以采取以下的解题技巧:1. 理解问题在开始解题之前,先要完全理解问题的背景和要求。


高考数学知识点解析斯托克斯公式与格林公式高考数学知识点解析:斯托克斯公式与格林公式在高考数学的众多知识点中,斯托克斯公式与格林公式是较为复杂但又十分重要的内容。
理解和掌握这两个公式,对于解决一些涉及曲线积分和曲面积分的问题具有关键作用。
首先,我们来认识一下格林公式。
格林公式建立了平面区域上的二重积分与沿着该区域边界的曲线积分之间的关系。
如果我们有一个闭区域 D 及其边界曲线 L,函数 P(x,y) 和 Q(x,y) 在 D 上具有一阶连续偏导数,那么格林公式可以表示为:∮L Pdx + Qdy =∬D (∂Q/∂x∂P/∂y)dxdy 。
为了更好地理解格林公式,我们来看一个简单的例子。
假设有一个平面区域是由一个半径为 r 的圆所围成的,我们要计算沿这个圆边界的曲线积分。
如果我们设P(x,y) =y ,Q(x,y) =x ,那么根据格林公式,曲线积分就可以转化为对这个圆区域的二重积分。
通过计算这个二重积分,就能得到曲线积分的结果。
那么,格林公式有什么用呢?它可以帮助我们简化曲线积分的计算。
有时候,直接计算曲线积分可能会比较困难,但通过格林公式将其转化为二重积分,可能会让计算变得更加简便。
接下来,我们再来看斯托克斯公式。
斯托克斯公式是格林公式在三维空间中的推广。
它建立了空间曲面上的曲面积分与沿着曲面边界的曲线积分之间的关系。
如果有一个有向曲面 S ,其边界曲线为Γ ,函数 P(x,y,z) 、Q(x,y,z) 和 R(x,y,z) 具有一阶连续偏导数,那么斯托克斯公式可以表示为:∮Γ Pdx + Qdy + Rdz =∬S (curlF)·ndS ,其中curlF 表示向量场 F =(P, Q, R) 的旋度,n 是曲面 S 的法向量。
同样,通过一个例子来帮助理解斯托克斯公式。
假设我们有一个半球面,要计算沿其边界圆的曲线积分。
运用斯托克斯公式,将曲线积分转化为对半球面的曲面积分,然后通过计算曲面积分来得到曲线积分的结果。

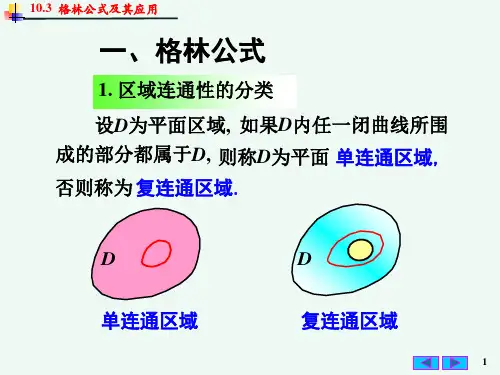

格林公式内容格林公式是高等数学中的一个重要公式,不过您这标题提到要从小学到高中的教材角度来写,可格林公式并不在这个阶段的教材里呀。
但既然接到了这个任务,那我就用比较通俗易懂的方式来跟您聊聊这个不在小学到高中教材里的格林公式,尽量让您有个初步的了解。
咱先来说说格林公式到底是啥。
简单来讲,格林公式把沿着一个封闭曲线的曲线积分和在这个曲线所围成的区域上的二重积分联系了起来。
这就好像是找到了两个不同世界之间的秘密通道,能让我们在计算的时候从一种方法轻松地转换到另一种方法。
比如说,有一个操场,您沿着操场的跑道跑一圈,这就是曲线积分。
而操场里面的整个区域呢,就相当于二重积分。
格林公式就告诉我们,这两者之间有着密切的关系。
我还记得之前给学生讲这个的时候,有个学生瞪着大眼睛问我:“老师,这有啥用啊?”我就笑着跟他说:“你想想,要是让你算沿着一个特别复杂的曲线走一圈的路程,多麻烦啊。
但如果能用格林公式转换成在一个区域里的计算,是不是就简单多啦?”那学生若有所思地点点头。
在实际应用中,格林公式的作用可大了。
比如说在物理学中,计算电场或者磁场的一些问题时,它就能派上大用场。
还有在工程学里,设计一些复杂的结构时,也能靠它来帮忙简化计算。
想象一下,有个工程师要设计一个形状奇特的零件,需要计算各种物理量。
如果没有格林公式,那他可能得花费大量的时间和精力去一点点计算。
但有了格林公式,就好像给他配备了一把神奇的钥匙,能打开快速解决问题的大门。
对于学习格林公式,重点在于理解它的原理和掌握运用的方法。
可别死记硬背,得通过多做练习题来真正掌握它的精髓。
总之,格林公式虽然有点复杂,但一旦掌握了,就能在数学和相关领域的学习和应用中如鱼得水。
希望您对格林公式能有个初步的认识啦!。


第六章 格林函数法本章利用高等数学中的格林(Green)公式导出调和函数的积分表达式,引进格林函数(又叫点源函数),它是一种广义函数.利用格林函数求解稳态的边值问题,这种方法叫格林函数法,它是解数学物理问题时常用的方法之一.§2.6.1 格林(Green )公式 调和函数的积分表达式2.6.1.1 格林公式设D 是以分片光滑的曲面S 为其边界的有界区域,函数P (x ,y ,z ), Q (x ,y ,z ), R (x ,y ,z )是在D 上连续,在区域D 内有连续偏导数的任意函数,则成立奥一高公式 V z R y Q x P D d (∂∂+∂∂+∂∂∫∫∫=∫∫++SS z n R y n Q x n P d )],cos(),cos(),cos([,这里d V 是体积元,n 是曲面S 的外法线方向,d S 为S 上的面积元.由此可以导出格林第二公式或格林公式:S nu v n v uV u v v u D S d d )()(∫∫∫∫∫∂∂−∂∂=Δ−Δ. 事实上,设函数u (x ,y ,z ), v (x ,y ,z )以及它们的所有的一阶偏导数在闭区域S D D U =上是连续的,u 、v 在D 内具有连续的二阶偏导数.令 P =x v u ∂∂, Q =yv u ∂∂, R =z v u ∂∂, 代入奥一高公式得到格林第一公式:V z v z u y v y u n v x u S n v uV v u DD S d d d )()(∂∂∂∂+∂∂∂∂+∂∂∂∂−∂∂=Δ∫∫∫∫∫∫∫∫ 这里是三维拉普拉斯(Laplace)算子,Δn∂∂表示曲面S 的外法线方向导数.如果引进梯度算子=∇k j v v v z yi x ∂∂+∂∂+∂∂ ,那么格林第一公式缩写成 ∫∫∫∫∫∫∫∫∇⋅∇−∂∂=ΔDS D V v u s n v uv v u d d d )()(,类似地,如果令 P =x u v ∂∂, Q =y u v ∂∂, R =zu v ∂∂,就有 ∫∫∫∫∫∫∫∫∇⋅∇−∂∂=ΔD D SV u v S n u v V u v d d )()(d 注意到向量的数性积的可交换性,上两式相减,得格林第二公式(又叫格林公式):S nu v n v u V u v v u D S d d )()∂∂−∂∂=Δ−Δ∫∫∫∫∫( . 2.6.1.2拉普拉斯方程的基本解在三维空间内,记),()()()(222N M r z y x r =−+−+−=ςηξ表示点M (x ,y ,z )、)(ςηξ,,N 之间的距离,利用复合函数求导的链式法则,对空间中任意固定的一点N ,函数r1除点N 外关于变量(x , y , z )处处满足拉普拉斯方程0=Δu ;注意到函数r1的特征,同样对于任意固定的一点M (x , y , z ),函数r1除点M 外,关于变量),,(ςηξ处处满足拉普拉斯方程,即0)1(=Δr, (N M ≠). 函数r1在求解拉普拉斯方程和泊松(Poisson)方程时有极重要的作用,通常把函数r1称为三维拉普拉斯方程或者泊松方程的基本解.同样,对于二维空间,函数),(1ln )()(1ln 1ln 22N M r y x r =−+−=ηξ 叫做二维拉普拉斯方程或泊松方程的基本解.2.6.1.3 调和函数的积分表达式仍以三维空间为例,利用格林公式不难得到三维空间调和函数的积分表达式.定理:(调和函数的积分表达式)设函数u (x , y , z )在闭区域D 上有连续的一阶偏导数,且u (x , y , z )在区域D 内调和(即0=Δu 在D 内成立),那么对于D 内任意固定的一点就有),,(0000z y x M ,])1(1[41)(0S nr u n u r M u S d ∂∂−∂∂=∫∫π D M ∈0 ,这里M 为点(x , y , z ),并有2020200)()()(),(z z y y x x M M r r −+−+−== .事实上,设为区域D 内任意固定的一点,M (x ,y ,z )为),,(0000z y x M D 上的一个动点,动点M 到定点M 0的距离2020200)()()(),(z z y y x x M M r r −+−+−== .注意到函数r 1除点M 0外,处处调和,M 0挖去.以M 0点为球心,充分小的正数(ρ>0),用表示这个小球的球面.记区域D 0M K ρ0M S ρ0M K ρ1=D \ (通常称区域D 内挖去点M 0M K ρ0).这时区域D 1的表面为.U S 0M S ρ于是函数u , v =r1在闭区域011M S S D D ρU U =上可用格林公式,就有∫∫∫∫∫∫∫∂∂−∂∂+∂∂−∂∂=Δ−ΔS S n u r n r u D S n u r n r u V u r r u M S 01)1)1((1)1((]1)1([ρd d d 因为在区域D 1内0)1(,0=Δ=Δru ,上式左边等于零,由此得 01)1()1)1((00=∂∂−∂∂+∂∂−∂∂∫∫∫∫∫∫S S n u r S S n r u S n u r n r u M M S ρρd d d 现在讨论上式左边的后两项积分.注意到,对区域D 1而言,小球面0M S ρ的外法线方向应指向球心M 0 , 与半径r 的方向刚好相反,因此在球面上有0M S ρ2211)1(1(ρ==∂∂−=∂∂rr r n r ,这样上式第二项积分有 )(44)(1)1(1212200M u M u s S u S S n r u M M ππρρρρρ===∂∂∫∫∫∫d d , 这里用到积分中值定理,M 1为球面上的某一点.0M S ρ对于上式第三项积分,用积分中值定理有||22044112M n u M n u S n u r M S ∂∂⋅=∂∂⋅⋅=∂∂∫∫πρπρρρd 这里M 2为上的某一点.0M S ρ 因为nu ∂∂在M 0点的邻域内是有界的,让0→ρ,则M 1、M 2趋于球心M 0 ,所以第三项积分趋于零,由此得0)(4)1)1((0=+∂∂−∂∂∫∫M u S n u r n r u Sπd . 从而得到有界区域D 内调和函数u 的积分表达式:S nr u n u r M u S d )1(1(41)(0∂∂−∂∂=∫∫π, D M ∈0. 这个公式说明,调和函数u 在区域D 内任意一点M 0处的值可以由它的边界S 上的值和它在边界S 上的法向导数nu ∂∂的值来确定,这对解边值问题提供了方便.推论:若u 在有界区域D 内是二阶连续的可微函数,则有积分表达式∫∫∫∫∫Δ−∂∂−∂∂=DS V r u S n r u v u r M u d d ππ41))1(1(41)(0,. D M ∈0这是因为在闭区域1D 上用格林公式,有 S n u r S n r u S n u r n r u V u D r S M d d d )11(()1)1((101∂∂−∂∂+∂∂−∂∂=Δ−∫∫∫∫∫∫∫ρ 类似上述的讨论,上式右端当0→ρ时,区域,其余都一样.D D →1对于二维情形,由于基本解为r1ln ,所以不难得到在二维有界区域D 内调和的函数u 的积分表达式:S nr u n u r M u C d )1(ln )1[ln(21)(0∂∂−∂∂=∫π, D M ∈0. 这里C 为区域D 的边界.对一般的在区域D 内有二阶连续可微函数u ,则积分表达式为S u r l n r u n u r M u DC d d Δ−∂∂−∂∂=∫∫∫)1(ln 21])1(ln )1[ln(21)(0ππ, .D M ∈0这两个公式的证明作为习题留给读者自己去证明.§2.6.2 拉普拉斯(Laplace )方程的狄里克雷问题2.6.2.1 边值问题的提法数学物理的不少问题都会归结为求拉普拉斯方程的解,根据边界条件的不同提法,可以把它的定解问题分为三类:第一边值问题,又称狄里克雷(Dirichlet)问题.求区域D 内调和,而在D 的边界S 上取已知值f 的函数u ,即狄里克雷问题的提法为:0=Δu , 在D 内,|u s =f 1(M ) , 在S 上.第二边值问题,又称诺伊曼(Neumann)问题,它的提法为: 0=Δu , 在D 内,),(|2M f nu S =∂∂ S M ∈. 第三边值问题,又称洛平(Robin)问题,它的提法为:, 在D 内,0=Δu ),(3M f u n u S=⎥⎦⎤⎢⎣⎡+∂∂βα S M ∈. 这里α、β为已知常数,且不同时为零;f 、f 、f 为已知函数.)(1M )(2M )(3M 如果以上的提法,针对求有界区域D 内的解,称为内问题,如果求区域的外部的解,称为外问题.对于狄里克雷问题、诺伊曼问题解的存在性,要用到积分方程的理论,由于已超出本书的范围,这里不再赘述,感兴趣的读者可以查阅相关的书籍,例如由沈乃录主编的《积分方程》一书,将会给你一个满意的解答.2.6.2.2 狄里克雷问题的格林函数 格林函数法我们重点来解狄里克雷问题.从调和函数u 的积分表达式出发,在区域D 内的调和函数u 的积分表达式为:S n r u nu r M u S d ∫∫∂−∂∂=)/1(1(41)(0π, D M ∈0. 这里由于狄里克雷问题0=Δu , 在D 内,|u s =f (M ) , 在∈M S 上.所以,积分表达式中的第二项u 在边界面S 上的值已知,用f (M )代替,就有S n r M f nu r M u S d ∫∫∂−∂∂=))/1()(1(41)(0π, D M ∈0, 这样求解的关键是如何从上式中消去带nu ∂∂(未知的)这一项. 由格林公式出发,要在区域D 内求一个函数g ,它在区域D 内调和(即0=Δg ),则格林公式为:S n u g ng uS d ∫∫∂∂−∂∂=)(0 用π41乘以上式,再和积分表达式相加,就有 S n g r M f n u g r M u S d ∫∫−∂−∂∂−=])/1()()1[(41)(0π, D M ∈0如果上式中在边界面S 上有g r −1=0,即=S g |r1,那末狄里克雷问题的解就是:S ng r M f M u S d ∫∫−∂−=])/1()([41)(0π, D M ∈0. 综上所述,欲解狄里克雷问题:0=Δu , 在D 内,|u s =f(M) , 在∈M S 上就转化为解另一个狄里克雷问题:0=Δg , 在D 内,=S g |r1 , ∈M S, 这里,);(0M M r r =);(0M M g g =,∈M S ,D M ∈0一般说来,函数也不是好求的,它与边界曲面S 的形状有关,但是不管怎么讲,给出了一个解狄里克雷问题的思路,并且对于一些特殊的区域D ,例如球体、半空间、圆域、半平面等可以用初等的方法求出函数g (M ; M );(0M M g 0)来.为了更清楚,我们令函数 );();(1);(000M M g M M r M M G −= 注意到基本解的特征,);(10M M r g (M ;M 0)的要求,对于函数G (M ;M 0)有两个基本性质:(1)除点D M ∈0外,函数G (M ;M 0)在区域D 内调和,即 0);(0=ΔM M G , M , M 0D ∈ 且0M M ≠ ;(2)在边界面S 上, ,0);(0=M M G ∈M ,S D M ∈0 . 通常把函数G (M ;M 0)称为拉普拉斯方程0=Δu 关于区域D 的狄里克雷问题的格林函数.用求格林函数G (M ;M 0)的方法解狄里克雷问题称为格林函数法.如果格林函数G (M ;M 0)求得,那么狄里克雷问题的解也就有了,并且为S M M G nM f M u S d );()(41)(00∫∫∂∂−=π , D M ∈0.对于二维的情形,完全类似地,可以得到 S nG M f M u C d ∫∂∂−=)(21)(0π , D M ∈0 为狄里克雷问题 C D M M f u D M u C=∂∈=∈=Δ),(,0| 的解,这里格林函数 );(1ln );(00M M g rM M G −=,作为习题留给读者自己去证明.例1. 球的狄里克雷问题和球的格林函数 球内狄里克雷问题的提法: , 在球内 0=Δu 2222R z y x <++ u=f (M ) , 在球面 上 2222R z y x =++这里 M =(x , y , z ).解: 先求球 的格林函数 2222R z y x <++ 设球内任一点,由此求满足另一个球狄里克雷问题:),(00,00z y x M );(0M M g 0);(0=ΔM M g , 在球内);(1);(00M M r M M g = , 在球面上 对于球而 2222R z y x <++M 1言,函数可以用初等的方 );(0M M g 法求得.记202020z y x ++=ρ,点 M 0的对称点为M 0R S 1,显然点M 1在球外,并在OM 0的延长线上(如图),由对称点的定义知:21R =ρρ⋅其中1ρ为OM 1的长,即 2121211z y x ++=ρ ,),,(1111z y x M =,由调和函数的基本解,这个应该是);(0M M g 1r A这种形式,这里 2121211)()()(z z y y x x r −+−+−= ,A 为待定常数.显然函数1r A在球内是调和的.问题是怎样确定常数A .由的第二个条件在球面上应为);(0M M g r 1.为区别起见,球面上的点记为),,(z y x M ′′′′.由于,所以在21R =⋅ρρM OM ′Δ0与中,是公共角,且夹这角的两边成比例1M M O ′ΔO ∠10OM M O M O OM ′=′,因此M OM ′Δ0与1M M O ′Δ相似,从而有M O OM M M M M ′=′′010,亦即R r r ρ=1,这样在球面上有OR S rr R 111=⋅ρ , 可见常数202020z y x RRA ++==ρ,所求的101);(r R M M g ⋅=ρ,因此球的格林函数为2121212020202020201100)()()(1)()()(1);(1);(1);(z z y y x x z y x Rz z y y x x M M r R M M r M M G −+−+−⋅++−−+−+−=⋅−=ρ得球内狄里克雷问题的解为S nG M f M u RS d ∂∂′−=∫∫)(41)(00π,().球∈0M 2222R z y x <++为了计算,还须将这公式化成便于积分的形式.采用球面坐标系.设点M ′的球坐标为),,(ϕθ′′R ,点M 0的球坐标为),,(00ϕθρ,将记为O∠α,于是在球面上,ORS nr nr ∂∂∂∂1(,)1(1有 02022)(1grad 11)1()1(n n ⋅∂∂+∂∂+∂∂−=⋅−=∂∂−=∂∂⋅∂∂=∂∂k zr j y r i x r r r r n r r n r r r n r 其中n 0是球面的外法线单位向量.O R S 在球面上, OR S M ′点的坐标为),,(z y x ′′′,由此r x x x r 0−′=∂∂ , r y y y r 0−′=∂∂ , rz z z r 0−′=∂∂ , 设r 0是r 方向上的单位向量,由此),cos(1)(1)1(200002n r r k r z z j r y y i r x x r n r −=⋅−′+−′+−′−=∂∂n , 同理 ),cos(1)1(1211n r r nr −=∂∂,这样),cos(),cos(1)1()1(12121n r r Rn r rn r n r R n G ρρ−=∂∂−∂∂=∂∂−为了简化上式,在与M OM ′Δ01M M O ′Δ中用余弦定理得Rr r R n r 2),cos(222ρ−+=, 12121212),cos(Rr r R n r ρ−+= , 注意到在球面上有OR S rr R 11=ρ,并且,于是有 21R =⋅ρρ3221212),cos(),cos(1Rr R n r r R n r rn G ρρ−=−=∂∂−, 从而球内狄里克雷问题的解化简为ϕθθραρρϕθπρπππ′′′+−−′′=−′=∫∫∫∫d d d sin ]cos 2[),(4)(41)(2322222003220R R R f RS rR M f R M u O RS这也叫球的泊松积分.利用M 0的对称点M 1构造格林函数的方法,叫做镜像法,物理学中又叫静电源象法.例 2. 半空间的狄里克雷问题.半空间的狄里克雷问题就是求一个在上半空间内的调和函数u (x , y, z ),且在边界面z =0上满足u (x , y , 0)=f (x , y ),即0>z⎪⎩⎪⎨⎧=>=Δ=),(0,0|0y x f u z u z解:设在半空间在z >0内任意一点,这里z ),(00,00z y x M 0>0,那么M 0关于平面的对称点M 0=z 1就是 ),(00,0z y x −.所以函 数2020201)()()(11z z y y x x r ++−+−=是半空间内的调和函数,并且在边界面z =0上,显然有0>z rr 111=,因此半空间z >0内的格林函数为20202020202010)()()(1)()()(111);(z z y y x x z z y y x x r r M M G ++−+−−−+−+−=−=对于半空间z >0,边界面z =0的外法线方向与z 轴的正向相反,于是z G nG ∂∂−=∂∂,这个半空间z >0的狄里克雷问题的解为S n G y x f z y x u z d ∫∫=∂∂−=0000),(41),,(π =S zG y x f z d ∫∫=∂∂0),(41π=y x z y y x x y x f z d d ∫∫+∞∞−+∞∞−+−+−232020200])()[(),(2π.§2.6.3 泊松方程的狄里克雷问题在研究有外力作用下的薄膜平衡和有热流的热平衡以及稳定电场的静电势等问题时,都会导出称谓泊松方程的数学物理方程.泊松方程的一般形式是),,(z y x F u u u u zz yy xx =++≡Δ,其中F (x , y , z )为已知函数.泊松方程的狄里克雷问题的提法是),,(z y x F u =Δ (x , y , z )D ∈, )(|M f u S= M 在D 的边界面S 上.对于在有界区域D 内有二阶连续的可微函数u (M ),有积分表达式V r uS n r u n u r M u DSd d ∫∫∫∫∫Δ−∂∂−∂∂=ππ41))1(1(41)(0, . D M ∈0设是区域);(0M M G D 的格林函数,就有);();(1);(000M M g M M r M M G −=这里函数为区域);(0M M g D 内的调和函数,在边界面S 上有r g S1|=,对格林公式S n u v n v u V u v v u D Sd d ()(∂∂−∂∂=Δ−Δ∫∫∫∫∫中用函数替代v ,再两边乘以);(0M M g π41得∫∫∫∫∫Δ+∂∂−∂∂=DSV u g S n u r n g ud d ππ41)1(410将以上两等式相加,消去S n ur Sd ∂∂∫∫141π项就得泊松方程狄里克雷问题的解为∫∫∫∫∫+∂∂−=DSV FG S n G fM u d d ππ4141)(0显然,上式第一项是定解问题0=Δu 在D 内,的解;第二项是定解问题的解f u S=|0,|==ΔSu F u 对于二维泊松方程的狄里克雷问题可以类似地求解.。