导体和电介质中的静电场及复习讲义
- 格式:ppt
- 大小:2.55 MB
- 文档页数:6
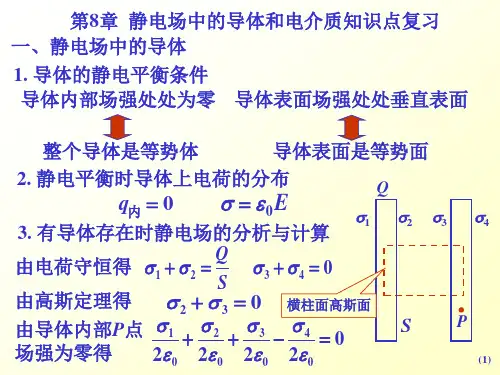

高中物理竞赛静电场中的导体与电介质知识点讲解一、金属导体的电结构导体:当物体的某部分带电后,能够将获得的电荷迅速向其它部分传布开,这种物体称为导电体(导体)。
绝缘体(电介质):物体的某部分带电后,其电荷只能停留在该部分,不能显著地向其它部分传布,这种物体称为绝缘体。
半导体:导电能力介于导体和电介质之间的物质。
★注意:导体、半导体和电介质之间无严格的界限,只是导电的程度不同。
金属导体的电结构:在各种金属导体中,由于原子最外层的价电子与原子核之间的吸引力很弱,很容易摆脱原子的束缚,脱离原来所属的原子在金属中自由移动,成为自由电子;组成金属的原子,由于失去部分价电子成为带正电的离子(晶体点阵)。
(如图)金属导体的电结构:带负电的自由电子和带正电的晶体点阵。
当导体不带电也不受外电场作用时,两种电荷在导体内均匀分布,没有宏观移动,只有微观的热运动。
二、静电感应与静电平衡如果我们把导体放入静电场E中,电场将驱动自由电荷定向运动,形成电流,使导体上的电荷重新分布,见下图(a)。
在电场的作用下导体上的电荷重新分布的过程叫静电感应,感应所产生的电荷分布称为感应电荷,按电荷守恒定律,感应电荷的总电量是零。
感应电荷会产生一个附加电场E',见下图(b),在导体内部这个电场的方向与原场E相反,其作用是削弱原电场。
随着静电感应的进行,感应电荷不断增加,附加电场增强,当导体中总电场的场强00E E E'=+=时,自由电荷的再分布过程停止,静电感应结束,导体达到静电平衡,见下图(c).三、导体的静电平衡条件导体的静电平衡条件:导体处于静电平衡时,导体内部各点的场强为零。
根据静电平衡的条件,可得出如下结论:(1)静电平衡下的导体是等势体,导体的表面是等势面。
(解释)(2)在导体表面外,靠近表面处一点的场强的大小与导体表面对应点处的电荷面密度成正比,方向与该处导体表面垂直。
对结论(2)给予证明:方向:由于电场线处处与等势面垂直,所以导体表面附近若存在电场,则场强方向必与表面垂直。





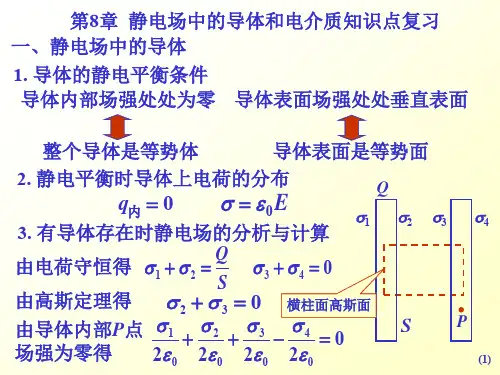

第第九九章章导导体体和和电电介介质质中中的的静静电电场场引言:一、导体、电介质、半导体导体:导电性能很好的材料;例如:各种金属、电解质溶液。
电介质(绝缘体):导电性能很差的材料;例如:云母、胶木等。
半导体:导电性能介于导体和绝缘体之间的材料;二、本章内容简介三、本章重点和难点1. 重点(1)导体的静电平衡性质;(2)空腔导体及静电屏蔽;(3)电容、电容器;2. 难点导体静电平衡下电场强度矢量、电势和电荷分布的计算;第一节静电场中的导体一、静电感应静电平衡1. 静电感应(1)金属导体的电结构从微观角度来看,金属导体是由带正电的晶格点阵和自由电子构成,晶格不动,相当于骨架,而自由电子可自由运动,充满整个导体,是公有化的。
例如:金属铜中的自由电子密度为:nCu=8⨯1028(m-3)。
当没有外电场时,导体中的正负电荷等量均匀分布,宏观上呈电中性。
(2)静电感应当导体处于外电场E0中时,电子受力后作定向运动,引起导体中电荷的重新分布。
结果在导体一侧因电子的堆积而出现负电荷,在另一侧因相对缺少负电荷而出现正电荷。
这就是静电感应现象,出现的电荷叫感应电荷。
2. 静电平衡不管导体原来是否带电和有无外电场的作用,导体内部和表面都没有电荷的宏观定向运动的状态称为导体的静电平衡状态。
(a)自由电子定向运动(b)静电平衡状态3. 静电平衡条件(静电平衡态下导体的电性质)(1)导体内部任何一点处的电场强度为零;导体表面处电场强度的方向,都与导体表面垂直。
(2)在静电平衡时,导体内上的电势处处相等,导体是一个等势体。
E证明:假设导体表面电场强度有切向分量,即τ≠0,则自由电子将沿导体表面有宏观定向运动,导体未达到静电平衡状态,和命题条件矛盾。
dUdU =0,=0E内=0,Eτ=0dldτ因为,所以,即导体为等势体,导体表面为等势面。
二、静电平衡时导体上电荷的分布1. 实心导体(1)处于静电平衡态的实心导体,其内部各处净电荷为零,电荷只能分布于导体外表面。
第二章静电场中的导体与电介质总结基本要求一理解静电场中导体处于静电平衡时的条件,并能从静电平衡条件来分析导体在静电场中的电荷分布和电场分布。
二了解电介质的极化及其微观机理,理解电位移矢量D 的概念,以及在各向同性介质中电位移矢量D和电场强度E 的关系。
理解电介质中高斯定理,并会用它来计算电介质中电场的电场强度。
三理解电容的定义,能计算常见电容器的电容四了解电场能量密度的概念。
思路与联系上一章我们讨论了真空中静电场,即空间中只有确定的红分布,无其他物体物体情况。
实际上,电场中总会存在其他物质的。
根据其导电能力我们把这种物质分为导体和电介质俩类。
首先,我们讨论导体在静电场中的静电感应现象,研究静电场中导体处于静电平衡时的条件和导体上的电荷分布,在此基础上讨论导体对静电场的影响,计算静电场中存在导体时的电场强度和电势分布。
接着,我们讨论电介质在静电场中的极化现象,研究电介质极化过程极化电荷的产生,在此基础上讨论电介质对静电场的影响,分析电介质中电场强度,并通过引入点位移矢量,得出电介质中的高斯定理。
利用静电场对导体和电介质的作用,可制成各种电容器。
这里对一些简单的电容器进行讨论,最后讨论了电场的能量。
对上述内容的讨论,要用到上一章的概念和定律,这一章是以上一章为基础的,是上一章的基本知识应用和推广。
内容一静电场中的导体把导体放在静电场中,导体内的自由电子由于受到电场力的作用而发生宏观运动,从而使导体上的电荷重新分布,这个过程一直持续到自由电子受到的电场力为零时为止。
这是导体处于静电平衡状态。
显然在导体处于静电平衡状态时,由于导体中的电荷所受的电场力为零,导体内任意点的电场强度必为零,因此,导体内各点的电场强度为零时导体处于静电平衡状态的必要条件。
从静电平衡时导体内部的电场强度为零这一点出发,可得到如下结果(1)导体为一等势体。
由于导体内部E=0, 所以由电势差定义V-V=⎰E⋅dl可知,导体内部任意俩点间的电势差为零,即导体为一等势体,导体表面为一等势面。