图解01背包问题

01背包问题（回溯法） 回溯法是⼀个既带有系统性⼜带有跳跃性的搜索算法。

它在包含问题的所有解的解空间树中，按深度优先策略，从根结点出发搜索解空间树。

算法搜索⾄解空间树的任意⼀结点时，先判断该结点是否包含问题的解。

如果肯定不包含，则跳过对该结点为根的⼦树搜索，逐层向其祖先结点回溯；否则，进⼊该⼦树，继续按深度优先策略搜索。

问题的解空间⽤回溯法解问题时，应明确定义问题的解空间。

问题的解空间⾄少包含问题的⼀个(最优)解。

对于 n=3 时的 0/1 背包问题，可⽤⼀棵完全⼆叉树表⽰解空间，如图所⽰：求解步骤1)针对所给问题，定义问题的解空间；2)确定易于搜索的解空间结构；3)以深度优先⽅式搜索解空间，并在搜索过程中⽤剪枝函数避免⽆效搜索。

常⽤的剪枝函数：⽤约束函数在扩展结点处剪去不满⾜约束的⼦树；⽤限界函数剪去得不到最优解的⼦树。

回溯法对解空间做深度优先搜索时，有递归回溯和迭代回溯（⾮递归）两种⽅法，但⼀般情况下⽤递归⽅法实现回溯法。

算法描述 解 0/1 背包问题的回溯法在搜索解空间树时，只要其左⼉⼦结点是⼀个可⾏结点，搜索就进⼊其左⼦树。

当右⼦树中有可能包含最优解时才进⼊右⼦树搜索。

否则将右⼦树剪去。

代码：public class Knapsack_Problem01 {double m=100; //背包最⼤容量int n=5; //物品的个数int[] w = {10,20,30,40,50}; //第i个物品的重量int[] v = {20,30,65,40,60}; //第i个物品的价值int[] a = new int[n]; //记录在树中的移动路径,为1的时候表⽰选择该组数据，为0的表⽰不选择该组数据int maxvalue = 0; //背包的最⼤权重值public static void main(String[] args){Knapsack_Problem01 p = new Knapsack_Problem01();p.Search(0);}public void Search(int i) //i表⽰递归深度{if(i>=n){CheckMax();}else {a[i] = 0;Search(i+1);a[i] = 1;Search(i+1);}}public void CheckMax(){int weight = 0;int value = 0;for(int i=0;i<n;i++) //判断是否达到上限{if(a[i] == 1){weight = weight + w[i];value = value + v[i];}}if(weight <= m){if(value >= maxvalue){maxvalue = value;System.out.print("最⼤价值是：" + maxvalue +" ");System.out.print("所选取的物品为(1代表选中，0代表不选中)： ");for(int j=0;j<n;j++){System.out.print(a[j]);System.out.print(' ');}System.out.print('\n');}}}}。

动态规划——01背包问题⼀、最基础的动态规划之⼀01背包问题是动态规划中最基础的问题之⼀，它的解法完美地体现了动态规划的思想和性质。

01背包问题最常见的问题形式是：给定n件物品的体积和价值，将他们尽可能地放⼊⼀个体积固定的背包，最⼤的价值可以是多少。

我们可以⽤费⽤c和价值v来描述⼀件物品，再设允许的最⼤花费为w。

只要n稍⼤，我们就不可能通过搜索来遍查所有组合的可能。

运⽤动态规划的思想，我们把原来的问题拆分为⼦问题，⼦问题再进⼀步拆分直⾄不可再分（初始值），随后从初始值开始，尽可能地求取每⼀个⼦问题的最优解，最终就能求得原问题的解。

由于不同的问题可能有相同的⼦问题，⼦问题存在⼤量重叠，我们需要额外的空间来存储已经求得的⼦问题的最优解。

这样，可以⼤幅度地降低时间复杂度。

有了这样的思想，我们来看01背包问题可以怎样拆分成⼦问题：要求解的问题是：在n件物品中最⼤花费为w能得到的最⼤价值。

显然，对于0 <= i <= n,0 <= j <= w，在前i件物品中最⼤花费为j能得到的最⼤价值。

可以使⽤数组dp[n + 1][w + 1]来存储所有的⼦问题，dp[i][j]就代表从前i件物品中选出总花费不超过j时的最⼤价值。

可知dp[0][j]值⼀定为零。

那么，该怎么递推求取所有⼦问题的解呢。

显⽽易见，要考虑在前i件物品中拿取，⾸先要考虑前i - 1件物品中拿取的最优情况。

当我们从第i - 1件物品递推到第i件时，我们就要考虑这件物品是拿，还是不拿，怎样收益最⼤。

①：⾸先，如果j < c[i]，那第i件物品是⽆论如何拿不了的，dp[i][j] = dp[i - 1][j];②：如果可以拿，那就要考虑拿了之后收益是否更⼤。

拿这件物品需要花费c[i]，除去这c[i]的⼦问题应该是dp[i - 1][j - c[i]]，这时，就要⽐较dp[i - 1][j]和dp[i - 1][j - c[i]] + v[i]，得出最优⽅案。

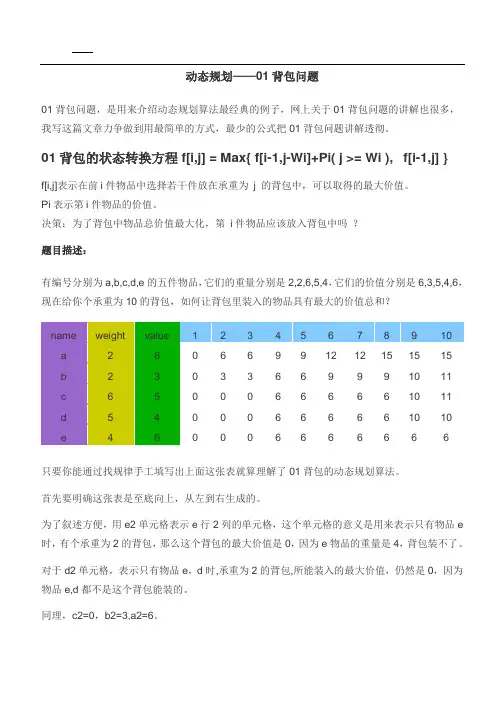
背包九讲P01: 01背包问题题目有N件物品和一个容量为V的背包。

第i件物品的费用是c[i]，价值是w[i]。

求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

基本思路这是最基础的背包问题，特点是：每种物品仅有一件，可以选择放或不放。

用子问题定义状态：即f[i][v]表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。

则其状态转移方程便是：f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]}。

这个方程非常重要，基本上所有跟背包相关的问题的方程都是由它衍生出来的。

所以有必要将它详细解释一下：“将前i件物品放入容量为v的背包中”这个子问题，若只考虑第i件物品的策略（放或不放），那么就可以转化为一个只牵扯前i-1件物品的问题。

如果不放第i件物品，那么问题就转化为“前i-1件物品放入容量为v的背包中”；如果放第i件物品，那么问题就转化为“前i-1件物品放入剩下的容量为v-c[i]的背包中”，此时能获得的最大价值就是f[i-1][v-c[i]]再加上通过放入第i件物品获得的价值w[i]。

注意f[i][v]有意义当且仅当存在一个前i件物品的子集，其费用总和为v。

所以按照这个方程递推完毕后，最终的答案并不一定是f[N] [V]，而是f[N][0..V]的最大值。

如果将状态的定义中的“恰”字去掉，在转移方程中就要再加入一项f[i][v-1]，这样就可以保证f[N] [V]就是最后的答案。

至于为什么这样就可以，由你自己来体会了。

优化空间复杂度以上方法的时间和空间复杂度均为O(N*V)，其中时间复杂度基本已经不能再优化了，但空间复杂度却可以优化到O(V)。

先考虑上面讲的基本思路如何实现，肯定是有一个主循环i=1..N，每次算出来二维数组f[i][0..V]的所有值。

那么，如果只用一个数组f [0..V]，能不能保证第i次循环结束后f[v]中表示的就是我们定义的状态f[i][v]呢？f[i][v]是由f[i-1][v]和f[i-1] [v-c[i]]两个子问题递推而来，能否保证在推f[i][v]时（也即在第i次主循环中推f[v]时）能够得到f[i-1][v]和f[i-1][v -c[i]]的值呢？事实上，这要求在每次主循环中我们以v=V..0的顺序推f[v]，这样才能保证推f[v]时f[v-c[i]]保存的是状态f[i -1][v-c[i]]的值。

动态规划——01背包问题01背包问题，是用来介绍动态规划算法最经典的例子，网上关于01背包问题的讲解也很多，我写这篇文章力争做到用最简单的方式，最少的公式把01背包问题讲解透彻。

01背包的状态转换方程 f[i,j] = Max{ f[i-1,j-Wi]+Pi( j >= Wi ), f[i-1,j] }f[i,j]表示在前i件物品中选择若干件放在承重为j 的背包中，可以取得的最大价值。

Pi表示第i件物品的价值。

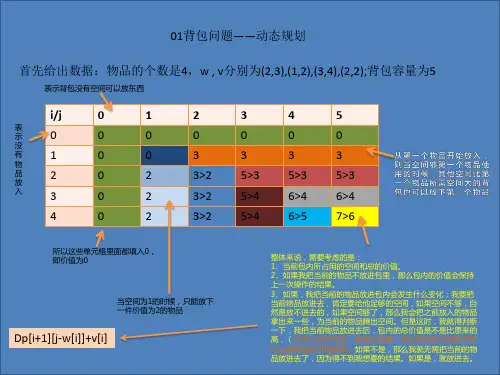
决策：为了背包中物品总价值最大化，第i件物品应该放入背包中吗？题目描述：有编号分别为a,b,c,d,e的五件物品，它们的重量分别是2,2,6,5,4，它们的价值分别是6,3,5,4,6，现在给你个承重为10的背包，如何让背包里装入的物品具有最大的价值总和？只要你能通过找规律手工填写出上面这张表就算理解了01背包的动态规划算法。

首先要明确这张表是至底向上，从左到右生成的。

为了叙述方便，用e2单元格表示e行2列的单元格，这个单元格的意义是用来表示只有物品e 时，有个承重为2的背包，那么这个背包的最大价值是0，因为e物品的重量是4，背包装不了。

对于d2单元格，表示只有物品e，d时,承重为2的背包,所能装入的最大价值，仍然是0，因为物品e,d都不是这个背包能装的。

同理，c2=0，b2=3,a2=6。

对于承重为8的背包，a8=15,是怎么得出的呢？根据01背包的状态转换方程，需要考察两个值，一个是f[i-1,j],对于这个例子来说就是b8的值9，另一个是f[i-1,j-Wi]+Pi；在这里， f[i-1,j]表示我有一个承重为8的背包，当只有物品b,c,d,e四件可选时，这个背包能装入的最大价值f[i-1,j-Wi]表示我有一个承重为6的背包（等于当前背包承重减去物品a的重量），当只有物品b,c,d,e四件可选时，这个背包能装入的最大价值f[i-1,j-Wi]就是指单元格b6,值为9，Pi指的是a物品的价值，即6由于f[i-1,j-Wi]+Pi = 9 + 6 = 15 大于f[i-1,j] = 9，所以物品a应该放入承重为8的背包以下是actionscript3 的代码[java]view plain copy1.public function get01PackageAnswer(bagItems:Array,bagSize:int):Array2.{3. var bagMatrix:Array=[];4. var i:int;5. var item:PackageItem;6.for(i=0;i<bagItems.length;i++)7. {8. bagMatrix[i] = [0];9. }10.for(i=1;i<=bagSize;i++)11. {12.for(var j:int=0;j<bagItems.length;j++)13. {14. item = bagItems[j] as PackageItem;15.if(item.weight > i)16. {17.//i背包转不下item18.if(j==0)19. {20. bagMatrix[j][i] = 0;21. }22.else23. {24. bagMatrix[j][i]=bagMatrix[j-1][i];25. }26. }27.else28. {29.//将item装入背包后的价值总和30. var itemInBag:int;31.if(j==0)32. {33. bagMatrix[j][i] = item.value;34.continue;35. }36.else37. {38. itemInBag = bagMatrix[j-1][i-item.weight]+item.value;39. }40. bagMatrix[j][i] = (bagMatrix[j-1][i] > itemInBag ? bagMatrix[j-1][i] : itemInBag)41. }42. }43. }44.//find answer45. var answers:Array=[];46. var curSize:int = bagSize;47.for(i=bagItems.length-1;i>=0;i--)48. {49. item = bagItems[i] as PackageItem;50.if(curSize==0)51. {52.break;53. }54.if(i==0 && curSize > 0)55. {56. answers.push();57.break;58. }59.if(bagMatrix[i][curSize]-bagMatrix[i-1][curSize-item.weight]==item.value)60. {61. answers.push();62. curSize -= item.weight;63. }64. }65.return answers;66.}PackageItem类[java]view plain copy1.public class PackageItem2.{3.public var name:String;4.public var weight:int;5.public var value:int;6.public function PackageItem(name:String,weight:int,value:int)7. { = name;9.this.weight = weight;10.this.value = value;11. }12.}测试代码[java]view plain copy1.var nameArr:Array=['a','b','c','d','e'];2.var weightArr:Array=[2,2,6,5,4];3.var valueArr:Array=[6,3,5,4,6];4.var bagItems:Array=[];5.for(var i:int=0;i<nameArr.length;i++)6.{7. var bagItem:PackageItem = new PackageItem(nameArr[i],weightArr[i],valueArr[i]);8. bagItems[i]=bagItem;9.}10.var arr:Array = ac.get01PackageAnswer(bagItems,10);出师表两汉：诸葛亮先帝创业未半而中道崩殂，今天下三分，益州疲弊，此诚危急存亡之秋也。

动态规划求解01背包问题问题给定n种物品和⼀个背包，物品(1<=i<=n)重量是w I ，其价值v i,背包容量为C,对每种物品只有两种选择：装⼊背包和不装⼊背包，即物品是不可能部分装⼊，部分不装⼊。

如何选择装⼊背包的物品，使其价值最⼤？想法该问题是最优化问题，求解此问题⼀般采⽤动态规划（dynamic plan），很容易证明该问题满⾜最优性原理。

动态规划的求解过程分三部分：⼀：划分⼦问题：将原问题划分为若⼲个⼦问题，每个⼦问题对应⼀个决策阶段，并且⼦问题之间具有重叠关系⼆：确定动态规划函数：根据⼦问题之间的重叠关系找到⼦问题满⾜递推关系式（即动态规划函数），这是动态规划的关键三：填写表格：设计表格，以⾃底向上的⽅式计算各个⼦问题的解并填表，实现动态规划过程。

思路：如何定义⼦问题？0/1背包可以看做是决策⼀个序列（x1,x2,x3,…,xn）,对任何⼀个变量xi的决策时xi=1还是xi=0. 设V(n,C)是将n个物品装⼊容量为C的背包时背包所获得的的最⼤价值，显然初始⼦问题是将前i个物品装如容量为0的背包中和把0个物品装⼊容量为j的背包中，这些情况背包价值为0即V(i,0)=V(0,j)=0 0<=i<=n, 0<=j<=C接下来考虑原问题的⼀部分，设V(I,j)表⽰将前i个物品装⼊容量为j的背包获得的最⼤价值，在决策xi时，已经确定了(x1,x2,…,xi-1)，则问题处于下列两种情况之⼀：1. 背包容量不⾜以装⼊物品i，则装⼊前i-1个物品的最⼤价值和装⼊前i个物品最⼤价值相同，即xi=0，背包价值没有增加2. 背包容量⾜以装⼊物品i，如果把物品i装⼊背包，则背包物品价值等于把前i-1个物品装⼊容量为j-wi的背包中的价值加上第i个物品的价值vi；如果第i个物品没有装⼊背包，则背包价值等于把前i-1个物品装⼊容量为j的背包中所取得的价值，显然，取⼆者最⼤价值作为把物品i装⼊容量为j的背包中的最优解，得到如下递推公式为了确定装⼊背包中的具体物品，从V(n,C)的值向前推，如果V（n，C）>V(n-1,C),则表明第n个物品被装⼊背包中，前n-1个物品被装⼊容量为C-wn的背包中；否则，第n个物品没有被装⼊背包中，前n-1个物品被装⼊容量为C的背包中，依次类推，直到确认第⼀个物品是否被装⼊背包中代码C++实现1. // dp_01Knapsack.cpp : 定义控制台应⽤程序的⼊⼝点。

01背包问题（01knapsackproblem）0 / 1 背包问题(0 / 1 knapsack problem)背包问题（Knapsack problem）是⼀种组合优化的问题。

问题可以描述为：给定⼀组物品，每种物品都有⾃⼰的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最⾼。

问题的名称来源于如何选择最合适的物品放置于给定背包中。

相似问题经常出现在商业、[组合数学]，[计算复杂性理论]、[密码学]和[应⽤数学]等领域中。

也可以将背包问题描述为，即在总重量不超过W的前提下，总价值是否能达到V。

1、题⽬描述假设商店中有如下3个商品，他们的重量和价格如下：索引重量价值011500143000232000假如你是⼀个⼩偷，你有⼀个重量为4的包，每个商品只能偷⼀次，请问你怎么偷才会使得最后的价值最⼤？2、分析这种问题⼀般可以⽤动态规划很好地解决。

但是如果我不⽤动态规划，⽽是⽤搜索所有情况来解决也可以，每个商品都有偷或不偷的选项，所以n个商品就有n^2种情况，所以⽤遍历的⽅法时间复杂度为O(n^2) n为商品的数量现在我们假设B(k, w)表⽰的是前k个商品，在背包容量为w的情况下能偷的最⾼价值当现在⾯对的第k个物品重量太重时：B(k, w) = B(k-1, w)，代表我在多了⼀个物品的选择的情况下，仍然和没有这件物品时的选择⼀样，所以结果也⼀样（因为我偷不了或者我不偷的情况）当第k个物品的重量我可以接受时：B(k, w) = B(k-1, w - 这件物品的重量) + 这件物品的价值代表我如果偷了这件物品，那剩下的w - 这件物品重量的空间可以容纳的最⼤价值就是在上⼀次选择时B(k-1, w - 这件物品的重量)的值。

再加上这件物品的价值就是我偷了这件物品的最⼤值。

所以，在衡量⼀个B(k, w)时，⾸先看⼀下能不能偷，能得话看⼀下偷还是不偷两个的最⼤值，就是B(k, w)的值，所以我们回到上⾯的问题，问题的解就是B(2，4)的值我们⽤⼆维数组 dp[][]来表⽰整个的过程可选商品 \ 背包容量012340号商品（1，1500）015001500150015000 ~ 1号商品（4，3000）015001500150030000 ~ 2号商品（3，2000）01500150020003500如图中加粗数字1500代表的是在有前两个商品，背包容量为2时可以偷的最⼤价值为1500图中加粗数字3000，即在有前2个商品，背包重量为4时，可以偷的最⼤价值为3000，这个数是这样算的：第⼆个商品（1号）重量为4，正好满⾜，如果偷的话所以价值为3000 + 0 = 3000如果不偷的话价值和只有1个商品，背包容量为4的价值⼀样，1500取最⼤值为3000所以问题的关键就在构建这个⼆维数组3、实现/*** 时间复杂度：O(n * capacity) n为商品数量，capacity为包的⼤⼩* 空间复杂度：O(n * capacity) 可以优化为capacity*/public class Main{/*** 0/1 背包问题* @param w w[i]代表i号物品的重量（从0开始）* @param v v[i]代表i号物品的价值（从0开始）* @param capacity 代表包的最⼤容量* @return 可以偷的商品的最⼤值*/public static int knapsack(int[] w, int[] v, int capacity){int goods = w.length; // 商品数int[][] dp = new int[goods][capacity + 1];// 初始化第⼀⾏,因为第⼀⾏上层没有元素了，即只有第⼀个商品时for(int j = 1; j <= capacity; j++){if(j >= w[0]) dp[0][j] = v[0];}// 前i个商品, 背包容量为j时偷得最⼤价值for(int i = 1; i < goods; i++) {for(int j = 1; j < capacity + 1; j++) {// 如果容量不够放下第i个商品if(w[i] > j) {dp[i][j] = dp[i-1][j];} else { // 如果可以放下这件商品dp[i][j] =Math.max(dp[i-1][j], v[i] + dp[i-1][j-w[i]]);}}}// System.out.println(Arrays.deepToString(dp));return dp[goods - 1][capacity];}}⽤滚动数组优化空间复杂度：因为如果我们从后往前构建每⼀⾏，那上⼀⾏保留的就可以在构建时候⽤/*** 时间复杂度：O(n * capacity) n为商品数量，capacity为包的⼤⼩* 空间复杂度：O(capacity)*/public class Main{/*** 0/1 背包问题* @param w w[i]代表i号物品的重量（从0开始）* @param v v[i]代表i号物品的价值（从0开始）* @param capacity 代表包的最⼤容量* @return 可以偷的商品的最⼤值*/public static int knapsack(int[] w, int[] v, int capacity){int goods = w.length; // 商品数int[] dp = new int[capacity + 1];// 前i个商品, 背包容量为j时偷得最⼤价值for(int i = 0; i < goods; i++) {for(int j = capacity; j > 0; j--) {// 如果能装下就更新，装不下就不更新(上⼀⾏的值)if(j - w[i] >= 0) {dp[j] = Math.max(dp[j], v[i] + dp[j - w[i]]);}}}return dp[capacity];}}。

一、问题描绘0/1 背包问题 :现有 n 种物件，对1<=i<=n，已知第i 种物件的重量为正整数W i，价值为正整数V i，背包能蒙受的最大载重量为正整数W ，现要求找出这n 种物件的一个子集，使得子集中物品的总重量不超出W 且总价值尽量大。

（注意：这里对每种物件或许全取或许一点都不取，不一样意只取一部分）二、算法剖析依据问题描绘，能够将其转变为以下的拘束条件和目标函数：nw i x i W(1)i1x i{ 0,1}( 1i n)nmax v i x i (2)i1于是，问题就归纳为找寻一个知足拘束条件（ 1 ），并使目标函数式（ 2 ）达到最大的解向量 X(x1, x2 , x3 ,......, x n ) 。

第一说明一下0-1 背包问题拥有最优解。

假定 (x1, x2 , x3 ,......, x n ) 是所给的问题的一个最优解，则 (x2 , x3,......, x n ) 是下边问题的nw i x i W w1x1 maxn一个最优解：i 2v i x i。

假如不是的话，设( y2, y3 ,......, y n ) 是这x i{ 0,1}( 2i n)i 2n n n个问题的一个最优解，则v i y i v i x i，且 w1x1w i y i W 。

因此，i 2i 2i 2n n nv1x1v i y i v1 x1v i x i v i x i，这说明 (x1, y2 , y3 ,........, y n ) 是所给的0-1 背包问i 2i 2i 1题比 ( x1 , x2 , x3 ,........, x n ) 更优的解，进而与假定矛盾。

穷举法：用穷举法解决0-1 背包问题，需要考虑给定n 个物件会合的所有子集，找出所有可能的子集（总重量不超出背包重量的子集），计算每个子集的总重量，而后在他们中找到价值最大的子集。

因为程序过于简单，在这里就不再给出，用实例说明求解过程。

分⽀限界法（三）——0-1背包问题（转）0-1背包问题问题描述给定n种物品和⼀背包。

物品i的重量是wi，其价值为pi，背包的容量为C。

问应如何选择装⼊背包的物品，使得装⼊背包中物品的总价值最⼤?0-1背包问题是⼀个特殊的整数规划问题。

例如：最优解为：(1,0,1)此时的价值为：6算法的思想⾸先，要对输⼊数据进⾏预处理，将各物品依其单位重量价值从⼤到⼩进⾏排列。

在下⾯描述的优先队列分⽀限界法中，节点的优先级由已装袋的物品价值加上剩下的最⼤单位重量价值的物品装满剩余容量的价值和。

算法⾸先检查当前扩展结点的左⼉⼦结点的可⾏性。

如果该左⼉⼦结点是可⾏结点，则将它加⼊到⼦集树和活结点优先队列中。

当前扩展结点的右⼉⼦结点⼀定是可⾏结点，仅当右⼉⼦结点满⾜上界约束时才将它加⼊⼦集树和活结点优先队列。

当扩展到叶节点时为问题的最优值。

上界函数b = cp; // 初始化为⽬前背包的重量// n表⽰物品总数，cleft为剩余空间while (i <= n && w[i] <= cleft) {cleft -= w[i]; // w[i]表⽰i所占空间b += p[i]; // p[i]表⽰i的价值i ++;}if (i <= n)b += p[i] / w[i] * cleft; // 装填剩余容量装满背包return b; // b为上界函数主算法循环体while (i != n+1) { // ⾮叶结点// 检查当前扩展结点的左⼉⼦结点Typew wt = cw + w[i];if (wt <= c) { // 左⼉⼦结点为可⾏结点if (cp+p[i] > bestp)bestp = cp + p[i];AddLiveNode(up, cp + p[i], cw + w[i], true, i+1);}up = Bound(i+1);// 检查当前扩展结点的右⼉⼦结点if (up >= bestp) // 右⼦树可能含最优解AddLiveNode(up, cp, cw, false, i+1); // 取下⼀个扩展节点（略）}实现（略）。

对01背包的分析与理解（图⽂）⾸先谢谢的(点击转到链接)让我学会01背包本⽂较长，但是长也意味着⽐较详细，希望您可以耐⼼读完。

题⽬:现在有⼀个背包(容器),它的体积(容量)为V,现在有N种物品(每个物品只有⼀个),每个物品的价值W[i]和占⽤空间C[i]都会由输⼊给出,现在问这个背包最多能携带总价值多少的物品?⼀.动态规划与递推解决01背包初步分析:0. 浅谈问题的分解在处理到第i个物品时,可以假设⼀共只有i个物品,如果前⾯i-1个物品的总的最⼤价值已经定下来了,那么第i个物品选不选将决定这1~i个物品能带来的总的最⼤价值刚刚是⾃顶向下,接下来反过来⾃底向上,第1个物品选不选可以轻松地⽤初始化解决,接下来处理第i个物品时,假设只有2个物品就好,那他处理完后前2个物品能带来的最⼤总价值就确定了,这样⼀直推下去,就可以推出前n个物品处理完后能带来的最⼤总价值1.分层考虑解决"每个物品最多只能装⼀次"每个物品只能装⼀次,那么就应该想到常⽤的⼀种⽅法,就是⽤数组的纵轴来解决,对于n个物品,为它赋予i=1~n的编号,那么数组的纵轴就有n层,每层只考虑装不装这个物品,那么分层考虑就可以解决最多装⼀个的问题了2.对0,1的理解对于每个背包,都只有0和1的情况,也就是拿或者不拿两种情况如果拿:那么空间就会减⼀点,⽐如说现在在考虑第i个物品拿不拿,如果说当前剩余空间为j,那么拿了之后空间就变为j-c[i],但是总价值却会增加⼀点,也就是增加w[i]如果不拿:那么空间不会变,还是j,但是总价值也不会变化3.限制条件所以对于这题来说有⼀个限制条件,就是空间不超出,然后⽬标就是在空间不超出的情况塞⼊物品使总价值最⼤,在前⾯,我们已经讲了数组的纵轴⽤来表⽰当前处理到第⼏个物品,那么只靠这个是不够的,⽽且这个数组的意义还没有讲这题就是限制条件(空间)与价值的平衡,你往背包中塞东西,价值多了,可是空间少了,这空间本来可能遇到性价⽐更⾼的物品但也可能没遇到4.具体的建⽴数组解决问题有了前⾯的限制情况和0,1的分析就可以建⽴数组了对于这个数组,结合题⽬要求来说,数组的意义肯定是当前的总价值,也就是第i个物品的总价值,那么题⽬还有⼀个限制条件,只靠⼀个n层的⼀维数组是不够的,还需要⼆维数组的横轴来分析当前的剩余容量所以我们有了⼀个数组可以来解决问题了,这个数组就叫f好了,然后它是⼀个⼆维数组,它的纵轴有i层,我希望它从i=1~n,不想从下标0开始是为了美观,然后这个⼆维数组的横轴代表着当前剩余的空间,就⽤j来表⽰,j=0~V,0就是没有空间的意思,V前⾯说了,是这个背包的总容量我们把这个⼆维数组建⽴在int main()的上⾯,所以它⼀开始全部都是0,省去了接下来赋初值为0的功夫有了数组f[i][j],然后对于每个f[i][j],它表⽰的是已经处理到第i个物品了,当剩余空间还有j时,能带有的最⼤价值,也就是说f[i][j]存储的是总价值说是总价值,可是涉及到放物品还是不放物品的问题,所以再细致点就是:当前剩余空间为j,⽤这j空间取分析第i个物品装不装如,处理执⾏完⾏为后,f[i][j]就表⽰了当前能装⼊的最⼤价值5.推导递推⽅程PS:谈⼀下对于动态规划递推的理解:处理到第i层时,假设前i-1层的数据都知道⽽且可以根据1~i-1层的数据推出i,那么就成功了⼀半了,因为第i层如此,那么第i-1层也可以根据1~i-2层推出,接下来只需要定义好数组的初始条件和注意边缘问题以及⼀些细节就可以了对于第i个物品,假设前i-1个物品都已经处理完如果第i个物品不能放⼊:这种情况就是背包已经满了,也就是当前剩余空间j⼩于第i个物品的占⽤空间C[i],这种情况下,空间没有变化,价值也没有变化,对于空间没有变化,即第i个物品的空间和第i-1个物品的空间j相同,对于价值没有变化,也就是数组f的值相同,然后开始利⽤前⾯的数据,也就是f[i][j]]=f[i-1][j]如果第i个物品不想放⼊,那么和不能放⼊其实是⼀样的,动机不同但结果相同,f[i][j]]=f[i-1][j]如果第i个物品放⼊了,那么f[i][j]=f[i-1][j-c[[i]]+w[i],下⾯解释⼀下这个公式,第i个物品的占⽤空间为c[i],价值为w[i],f[i-1][j-c[[i]]+w[i]表⽰前i-1个物品在给它们j-c[[i]空间时能带来的最⼤价值再回到第i个物品的⾓度,此时有j个空间,如果已经确定要放⼊,为了使空间充分利⽤,肯定是这j个空间只分c[i](刚好够塞下第i个物品),剩下的j-c[[i]全部给前⾯i-1个物品⾃由发挥,反正前⾯f[i-1][j-c[[i]]已经知道了,然后前⾯i-1个物品⽤j-c[i]的空间能带来最⼤的利益f[i-1][j-c[[i]],第i个物品⽤c[i]的空间带来利益w[i],所以如果第i个物品放⼊后,总利益是f[i][j]=f[i-1][j-c[[i]]+w[i]但是,长远来说,有⼀些偏极端情况,放⼊这个物品,也许它价值w[i]很⾼,但是它占⽤空间c[i]也⼤,它的性价⽐可能很低,所以这时候就需要max函数了当还有空间时:F[i,j] = max[F[i−1,j],F[i−1,j−C[i]] + W[i]当空间不够时:F[i,j] = F[i−1,j]下⾯⼀个个解释:当还有空间时:这时有两种⽅法,放还是不放,如果放,那么利益由两段组成1~i-1是⼀段,i是另⼀段;如果不妨,那么利益和上⼀层剩j空间时相同,这两个东西⼤⼩需要⽐较,因为如果放⼊,虽然加上了w[i],利益,可是冲击了前i-1个物品的利益,如果不放,那么没有收获到第i个物品的利益,但是把原来属于1~i的空间j,分给了1~i-1个物品,说不定前1~i-1的每个物品都空间⼩,价值⾼,性价⽐⾼呢?当空间不够时,它也只能F[i,j] = F[i−1,j]了,没有选择的余地#include<bits/stdc++.h>//万能头⽂件#define ll long longusing namespace std;const ll maxn=100;ll n,v,f[maxn][maxn];ll c[maxn];//每个物品占⽤空间ll w[maxn];//每个物品的价值int main(){cin>>n>>v;for(ll i=1;i<=n;i++)scanf("%lld",&c[i]);for(ll i=1;i<=n;i++)scanf("%lld",&w[i]);for(ll i=1;i<=n;i++)//第i个物品for(ll j=v;j>=0;j--)//剩余空间j{if(j >= c[i])//如果装得下f[i][j]=max( f[i-1][j-c[i]]+w[i],f[i-1][j]);else//如果装不下f[i][j]=f[i-1][j];}cout<<f[n][v]<<endl;//输出答案}01背包普通版代码点击加号展开代码,如果点不开可以看底下的代码⼆.01背包的空间优化有了前⾯基础版01背包的学习,现在学习这个就容易多了1.何为空间优化,为什么要空间优化在01背包中通过对数组的优化(⽤了滚动数组的⽅法),可以使本来N*V的空间复杂度降低到V,也就是把关于第⼏个物品的N去掉了(下⾯会解释为什么可以这么做)⾄于为什么要空间优化,⾸先是因为递推本来就是⽤空间换时间,消耗的空间⽐较⼤,然后关于算法的竞赛⼀般都会有空间的限制要求,最后,在找⼯作⾯试时,⾯试官肯定会问⼀些优化的问题,平时养成优化的习惯⾯试时也有好处2.为什么这题可以降维通过观察可以发现对于普通版的01背包递推式,f[i][...]只和f[i-1][...]有关,那么我们可以⽤⼀种占⽤,⼀种滚动的⽅法来循环使⽤数组的空间,所以这个⽅法叫滚动数组,对于将来肯定⽤不到的数据,直接滚动覆盖即可,具体的如何滚动会放下⾯讲还有就是滚动数组的缺点是牺牲了抹除了⼤量数据,不是每道题都可以⽤,但是在这,答案刚好是递推的最后⼀步,所以直接输出即可,递推完后不需要调⽤那些已经没了的数据,所以这题可以下⾯先画个图理解⼀下滚动的⼤致概念反正就是不断覆盖的过程3.这题如何具体优化下⾯开始具体化的分析对于第i层,它只和第i-1层有关,但是对于剩余空间j⽆法优化,所以现在拿i开⼑,把他砍掉,⽤⼀个长度为V(总空间)的数组来表⽰,然后每次相邻的两个i和i-1在上⾯⼀直滚动所以现在建⽴⼀个数组f[V],⼀维数组⼤⼩为V⾸先建⽴两个复合for循环for(i=1~n) for(j=v~0)记住这⾥第⼆层循环必须是v~0⽽不是0~v,先记着,后⾯会解释,接下来的分析建议配合下⾯图⽚学习然后在循环的过程中,还是⽼样⼦,假设我们已经循环到i=2这层了(也就是说i=1已经循环完了),然后对于i=2这⼀层,我们对j循环,j从v到0假如现在j=v,我们让f[j]=max(f[j],f[j-c[i]]+w[i])在没有覆盖之前,所有的f数据都是属于上⼀层也就是第⼀层的,我们就当作i-1层数据已经准备好了,然后把max内的拆成两半分析,对于f[j]=f[j]就是不放的情况,那么总价值没有改变,所以对于f[j]=f[j]就是形式上的更新数据,把i-1层的f[j],给了i-1层的f[j]...对于f[j]=f[j-c[i]]+w[i],那个w[i]是肯定要加的不⽤讨论,然后我们观察⼀下,对于下标j-c[i]是不是肯定会⼩于j,那么如果说j从V~0也就是从最⼤到最⼩,每次赋值处理都是从前⾯的格⼦看看数据参考,并没有修改再详细点说的话就是对于f[j]=f[j-c[i]]+w[i],f[j-c[i]]是第i-1层的东西,让j=v~0是为了让f数组每次滚动覆盖时都是覆盖接下来不需要⽤的位置,⽐如说处理到第f[8]位时,假如接下来的max 判定后⾯那种⽅法总价值⼤,然后假设c[i]=3,这时后就相当与f[8]=f[8-c[i]=5]+w[i],我们这⾥只是参考了f[5]的数据,并没有改变它,因为说不定计算新⼀轮f[6]时⼜要⽤到旧的f[5]呢,可是我们刷新了f[8]的数字后,再j--,计算f[7],再j--,计算f[6],都不会再⽤到f[8]这个数据,这是由于f[j-c[i]] 中的减c[i]导致的,反之,假若我们让j=0~v,就可能出现新数据被新数据覆盖的结果,我们是有"底线"的,只允许新数据覆盖旧数据对于j,如果要处理f[j]=max(f[j],f[j-c[i]]+w[i]),就得当j>=c[i]时处理,因为如果j<c[i],那么j-c[i]为负,下标负的情况没必要考虑,如果考虑了还可能会溢出其实对于max,还⽤另⼀个⼩东西代替,有没有发现,如果f[j-c[i]]+w[i]>f[j],就选f[j-c[i]]+w[i],如果f[j-c[i]]+w[i]<f[j],那选f[j]和没选⼀样,所以待会的空间优化版省掉了max函数,少⽤⼀种函数#include<bits/stdc++.h>//万能头⽂件#define ll long longusing namespace std;const ll maxn=100;ll n,v,f[maxn];ll c[maxn];//每个物品占⽤空间ll w[maxn];//每个物品的价值int main(){cin>>n>>v;for(ll i=1;i<=n;i++)scanf("%lld",&c[i]);for(ll i=1;i<=n;i++)scanf("%lld",&w[i]);for(ll i=1;i<=n;i++)//第i个物品for(ll j=v;j>=1;j--)//剩余空间j{if(f[j]<=f[j-c[i]]+w[i] && j-c[i]>=0 )//⼆维数组变⼀维数组f[j]=f[j-c[i]]+w[i];//如果值得改变并且j的空间还装得下就赋新值}cout<<f[v]<<endl;//输出答案}空间优化版01背包点击"+"号展开代码,为了排版好看把代码折叠了,为了防⽌有⼈点不开⽂章底部还有⼀份没折叠的三.初始化的细节初始化有两种,⼀种情况是只要求价值最⼤,另外⼀种是要求完全刚好塞满,第⼀种的初始化是赋值为0,第⼆种的初始化是赋值为负⽆穷,因为没有塞满,所以数据实际上不存在,也就是让不存在的数不现实化,让与这种数相关的数据都不可⽤化下⾯贴⼀些背包九讲的⽂字1.4初始化的细节问题我们看到的求最优解的背包问题题⽬中，事实上有两种不太相同的问法。

贪⼼算法-01背包问题1、问题描述：给定n种物品和⼀背包。

物品i的重量是wi，其价值为vi，背包的容量为C。

问:应如何选择装⼊背包的物品，使得装⼊背包中物品的总价值最⼤?形式化描述：给定c >0, wi >0, vi >0 , 1≤i≤n.要求找⼀n元向量(x1,x2,…,xn,), xi∈{0,1}, ∋ ∑ wi xi≤c,且∑ vi xi达最⼤.即⼀个特殊的整数规划问题。

2、最优性原理：设(y1,y2,…,yn)是 (3.4.1)的⼀个最优解.则(y2,…,yn)是下⾯相应⼦问题的⼀个最优解:证明:使⽤反证法。

若不然,设(z2,z3,…,zn)是上述⼦问题的⼀个最优解,⽽(y2,y3,…,yn)不是它的最优解。

显然有∑vizi > ∑viyi (i=2,…,n)且 w1y1+ ∑wizi<= c因此 v1y1+ ∑vizi (i=2,…,n) > ∑ viyi, (i=1,…,n)说明(y1,z2, z3,…,zn)是(3.4.1)0-1背包问题的⼀个更优解,导出(y1,y2,…,yn)不是背包问题的最优解,⽭盾。

3、递推关系：设所给0-1背包问题的⼦问题的最优值为m(i，j)，即m(i，j)是背包容量为j，可选择物品为i，i+1，…，n时0-1背包问题的最优值。

由0-1背包问题的最优⼦结构性质，可以建⽴计算m(i，j)的递归式:注:(3.4.3)式此时背包容量为j，可选择物品为i。

此时在对xi作出决策之后,问题处于两种状态之⼀:(1)背包剩余容量是j,没产⽣任何效益；(2)剩余容量j-wi,效益值增长了vi ；使⽤递归C++代码如下：#include<iostream>using namespace std;const int N=3;const int W=50;int weights[N+1]={0,10,20,30};int values[N+1]={0,60,100,120};int V[N+1][W+1]={0};int knapsack(int i,int j){int value;if(V[i][j]<0){if(j<weights[i]){value=knapsack(i-1,j);}else{value=max(knapsack(i-1,j),values[i]+knapsack(i-1,j-weights[i]));}V[i][j]=value;}return V[i][j];}int main(){int i,j;for(i=1;i<=N;i++)for(j=1;j<=W;j++)V[i][j]=-1;cout<<knapsack(3,50)<<endl;cout<<endl;}不使⽤递归的C++代码：简单⼀点的修改//3d10-1 动态规划背包问题#include <iostream>using namespace std;const int N = 4;void Knapsack(int v[],int w[],int c,int n,int m[][10]);void Traceback(int m[][10],int w[],int c,int n,int x[]);int main(){int c=8;int v[]={0,2,1,4,3},w[]={0,1,4,2,3};//下标从1开始int x[N+1];int m[10][10];cout<<"待装物品重量分别为："<<endl;for(int i=1; i<=N; i++){cout<<w[i]<<" ";}cout<<endl;cout<<"待装物品价值分别为："<<endl;for(int i=1; i<=N; i++){cout<<v[i]<<" ";}cout<<endl;Knapsack(v,w,c,N,m);cout<<"背包能装的最⼤价值为："<<m[1][c]<<endl;Traceback(m,w,c,N,x);cout<<"背包装下的物品编号为："<<endl;for(int i=1; i<=N; i++){if(x[i]==1){cout<<i<<" ";}}cout<<endl;return 0;}void Knapsack(int v[],int w[],int c,int n,int m[][10]){int jMax = min(w[n]-1,c);//背包剩余容量上限范围[0~w[n]-1] for(int j=0; j<=jMax;j++){m[n][j]=0;}for(int j=w[n]; j<=c; j++)//限制范围[w[n]~c]{m[n][j] = v[n];}for(int i=n-1; i>1; i--){jMax = min(w[i]-1,c);for(int j=0; j<=jMax; j++)//背包不同剩余容量j<=jMax<c{m[i][j] = m[i+1][j];//没产⽣任何效益}for(int j=w[i]; j<=c; j++) //背包不同剩余容量j-wi >c{m[i][j] = max(m[i+1][j],m[i+1][j-w[i]]+v[i]);//效益值增长vi }}m[1][c] = m[2][c];if(c>=w[1]){m[1][c] = max(m[1][c],m[2][c-w[1]]+v[1]);}}//x[]数组存储对应物品0-1向量,0不装⼊背包，1表⽰装⼊背包void Traceback(int m[][10],int w[],int c,int n,int x[]){for(int i=1; i<n; i++){if(m[i][c] == m[i+1][c]){x[i]=0;}else{x[i]=1;c-=w[i];}}x[n]=(m[n][c])?1:0;}运⾏结果：算法执⾏过程对m[][]填表及Traceback回溯过程如图所⽰：从m(i，j)的递归式容易看出，算法Knapsack需要O(nc)计算时间; Traceback需O(n)计算时间；算法总体需要O(nc)计算时间。