网格模型化简综述’

大型网格模型简化和多分辨率技术综述章节一：引言- 回顾网格模型的发展历程- 分析网格模型的优势和不足- 简述本论文的研究和目的章节二：网格模型简化技术- 贪心算法- 顶点合并算法- 边塌缩算法- 基于误差度量的算法- 骨架化简算法章节三：多分辨率技术- 金字塔技术- 线性变换技术- 基于三角形分割的技术- 局部分辨率技术章节四：综合应用案例- 静态场景下的大规模网格简化- 动态场景下的网格细节管理- 网格拓扑结构的优化和管理章节五：结论与展望- 总结网格模型简化和多分辨率技术的研究现状和应用情况- 展望未来研究方向和挑战- 强调该领域的重要性和应用前景第一章节：引言目前，网格模型已成为了三维计算机图形学和计算机视觉领域中最常用的表示三维物体的方法之一。

它可以把三维物体表示为由三角形面片连接而成的网格，将其转化为一组数据，方便进行渲染、编辑、分析和处理等操作。

然而，大规模的网格模型往往存在着存储量大、计算量大、渲染效率低、交互性差等缺陷，因此需要进行模型简化和多分辨率技术的改进。

本文将对网格模型简化和多分辨率技术进行综述，旨在全面掌握这两类技术的基本原理和最新应用进展。

本章的主要内容包括：回顾网格模型的发展历程、分析网格模型的优势和不足、简述本论文的研究和目的。

一、网格模型的发展历程网格模型出现的历史可以追溯到上世纪70年代初，当时它主要作为计算机辅助设计（CAD）中的一个工具，用于快速地建模和分析三维模型。

由于计算机性能的限制，当时的网格模型主要采用四面体和棱柱等几何体网格结构，实现简单但效率低下。

随着计算机硬件和计算机图形学理论的发展，网格模型逐渐成为三维建模和可视化中的核心表示方式。

1980年代中期，三角形网格结构逐渐被广泛采用，这是因为三角网格在表示造型精细的同时，几何数据量也不会过于庞大。

从1990年代开始，人们逐渐开始运用曲面拟合技术对三角形网格进行精细化、光滑化处理，成为了现代三维建模的主要方法之一。

第十三讲网格模型一. 慨述怎样将现实中的一个物体，比如，一只花瓶，一个足球，甚至一架大的战斗机，在电脑屏幕上显示呢？我们一般会这样做：1. 先把该物体放在一个虚拟的三维坐标系中，该坐标称为局部坐标系(Local Space), 一般以物体的中心作为坐标原点，采用左手坐标系。

2. 然后，对坐标系中的物体进行点采样(Point Sample), 这些采样点按一定顺序连接成为一系列的小平面（三角形或共面的四边形，五边形等），这些小平面称为图元(Primitive), 3D 引擎会处理每一个图元，称为一个独立的渲染单位。

这样取样后的物体看起来像是由许许多多的三角形，四边形或五边形组成的，就像网一样，我们称为一个网格(Mesh).这个采样过程又可称为物体的3D建模。

当然现在都有功能非常强大的3D建模工具，例如，3D Max, 3D Cool等建模工具，省去了我们这方面的许多工作。

3. 我们纪录这些顶点数据和连线情况到一个文件中，3D引擎读取这些数据，依次渲染每一个图元，就能在显示屏幕上再现物体。

当然了，取样的点越多，再现的物体也会越逼真，要处理的数据量也越大。

二. D3D中的网格(Mesh)1、子集和属性缓存网格模型都由一个或多个子集（subset）组成，其中每个子集都具有一组相同材质、纹理和绘制状态等属性的三角形集合。

为了区分网格中的不同子集，每个子集都被指定了一个唯一的属性ID，而且网格中的每个三角形也被指定了该三角形所属子集的属性ID。

在mesh中的每个三角形都与一个属性ID相关联，表示该三角形属于该子集。

例如，上图中组成地板的三角形具有属性ID0，它表示这些三角形属于子集0。

同样，组成墙的三角形具有属性ID1，它表示这些三角形属于子集1。

三角形的属性ID存储在mesh的属性缓存中，它是一个DWORD数组。

因为每个面对应属性缓存中的一项，所以属性缓存中的项目数等于mesh中的面的个数。

属性缓存中的项目和索引缓存中定义的三角形一一对应。

网格算法的原理
网格算法是一种常用的计算机图形学算法，用于将二维空间划分为规则的网格格点，以实现图形模型的离散化表示和各类计算操作。

其原理是将整个空间划分为一个个小的单元格，每个单元格都具有固定的大小。

网格算法的主要思想是将空间划分为一系列的网格单元，每个单元格代表了一个离散化的小区域。

这些单元格可以用于表示图形对象的形状、位置、颜色等属性。

在网格算法中，常用的单元格形状包括正方形和长方形。

每个单元格可以表示一个像素、一个点或者更大的对象。

其中，最小的单元格称为基本单元。

通过将空间划分为网格单元，可以将图形模型转换为离散化的数据结构。

这样，可以使用一组有限的数据结构来表示整个图形模型，从而简化图形模型的处理和操作。

网格算法的主要应用包括图形渲染、图形碰撞检测、物理模拟等。

在图形渲染中，可以根据每个网格单元的属性来确定其颜色，从而生成图像。

在图形碰撞检测中，可以通过判断不同网格单元是否相交来判断碰撞是否发生。

在物理模拟中，可以根据每个网格单元的属性来计算物理效应，如重力、摩擦力等。

总之，网格算法通过将空间划分为网格单元，将图形模型离散化表示，以实现各种计算操作。

这种离散化的表示方式使得图形计算更加高效和方便。

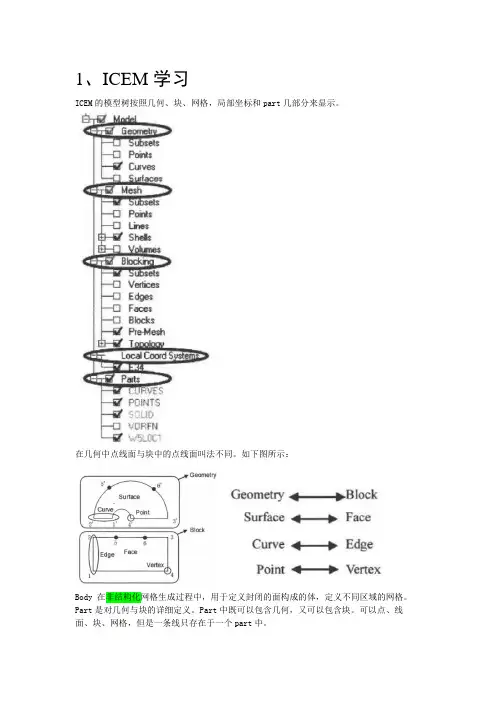
1、ICEM学习ICEM的模型树按照几何、块、网格，局部坐标和part几部分来显示。

在几何中点线面与块中的点线面叫法不同。

如下图所示：Body 在非结构化网格生成过程中，用于定义封闭的面构成的体，定义不同区域的网格。

Part是对几何与块的详细定义。

Part中既可以包含几何，又可以包含块。

可以点、线面、块、网格，但是一条线只存在于一个part中。

网格单元类型：1.网格生成方法：1、AutoBlock2、Patch Dependent3、Patch Independent4.Shrinkwrap壳、面生成网格的过程：2.Tolerance与颜色问题：导入ICEM中的模型首先要进行模型修复。

导入到ICEM中的几何模型要可能会出现三种颜色curve，红颜色的正常，黄色的为不连续的，蓝色的为重复的。

黄色的是单个面的边界（二维），红色的是两个面的交界线，蓝色的是三个/三个以上面相交的交线。

（出现蓝线是没有问题的，表明这个线是两个面以上的共线，只要不出现黄线就可以，黄线表示这儿有裂缝。

）黄线表示出现了洞，可能是面丢失了，造成蓝线的原因是有面体重叠了，你得删除多余的面体。

黄色的线表有孔或缝隙。

绿色的线直接删除。

白色的边和顶点：这些边位于不同的材料体间，它们和被关联的顶点将被映射到这些材料体中最贴近的CAD 表面，而且这些边上的顶点只能在表面内移动。

蓝色的边和顶点：这些边位于体内部。

它们的顶点也是蓝色的，可以在选择之前沿边拖拽。

绿色的边和顶点：这些边和关联的顶点是映射到曲线的，这些顶点只能在它所映射的曲线上移动。

红色的顶点：这些顶点是映射到指定的点的。

导入的模型必须是封闭的面，线是红色的。

自动生成翼型的网格。

3.equivalence将同一空间位置的重复节点消除（通常，消除ID好较大的节点，保留ID好较小的节点），只保留一个节点，一般与“Verify”配合使用，这种方法可通过任何FEM定义（单元的相关定义、MPC等式、载荷、边界条件等）、几何定义和组等实现。

摘要：针对二次误差测度（QEM）网格简化算法全局几何特征信息损失严重的缺点，提出一种具有结构感知功能面向城市三维模型重建的网格简化算法。

该算法顾及城市影像中平面结构特征，以代理平面为全局特征约束条件，使模型在简化过程中全局结构特征更多地被保持，以利于多层次细节模型（LOD技术）、网格优化提速等模型后续操作。

以倾斜摄影获取影像生成的初始三角网格模型为试验数据，采用所给算法对其进行网格简化并与QEM算法进行对比。

结果表明：所给算法简化精度及简化效率均优于QEM算法。

关键词：网格简化场景结构感知三维重建平面检测Structure-aware simplified algorithm of mesh model for urban sceneAbstract: Aiming at the shortcomings of global geometric feature loss caused by quadratic error measure (QEM) mesh simplification algorithm, a structure-aware mesh simplification algorithm for urban environment 3D model reconstruction is proposed. The algorithm takes into account the planar structure features in urban images, and uses the proxy plane as the global feature constraint in the simplification process, so that the global structural features of the model are more preserved during the simplification process, which is conducive to the refinement and progressive transmission of the model (LOD technology), grid optimization speedup and other model follow-up operations. In this paper, the initial manifold triangle mesh model generated by oblique photography is taken as the experimental data. The proposed algorithm is used to simplify the mesh and compare with the QEM algorithm, which experimental results show that the proposed algorithm has excellent simplification accuracy and simplified efficiency than the QEM algorithm.Key words: mesh simplification scene structure aware3D reconstruction plane detection三维重建是数字城市建设的重要内容之一。

一种保持特征的网格简化算法网格简化算法是计算机图形学中常用的一种算法，用于减少图像的复杂度，保留重要的特征。

传统的重采样算法可以简化网格但会损失许多细节，而保持特征的网格简化算法则对应于一种技术，可以简化网格的复杂度，而又保留重要的特征。

保持特征的网格简化算法可以有效地在保持图像特征的同时缩减图像的大小，从而节省存储空间，提高传输速度。

同时，该算法可以有效地减少计算机图形学中强调的细节，以减少网格的复杂度，实现真实的图像渲染效果。

保持特征的网格简化算法主要包括以下两个方面：信息保持和简化处理。

信息保持方面，算法在模型重建过程中，首先保留原始模型中高层特征，然后再将网格细分点的数量进行优化，以确保保留的特征与原始模型相似。

简化处理方面，算法通过属性可视化技术，可以自动或手动分析原始模型的特征，使网格重建的结果能够更精确地反映原始模型的特征，从而实现简化处理。

保持特征的网格简化算法有多种应用，例如可以用于三维视觉跟踪系统中的建模，可以用于网页上的动画渲染，还可以用于视频游戏引擎中的特效渲染等等。

尽管保持特征的网格简化算法在网格减少和特征保持方面具有显著的性能，但它也有一些缺点。

首先，由于保持特征的网格简化算法在保留特征同时减少网格复杂度，复杂度较高，会导致计算时间较长，这对于实时处理等应用程序不太适用。

其次，网格简化算法需要明确地界定要保留的细节，这会限制应用范围。

通过以上分析，我们可以看出，保持特征的网格简化算法在简化网格的同时保留了重要的特征，具有节省存储和传输空间，提高渲染效率，减少细节复杂度等优点，广泛应用于三维视觉跟踪系统，动画渲染，视频游戏引擎等等，但也存在一些缺点，如时间复杂度高，应用范围有限等。

因此，为了发挥最大的效果，应根据具体的应用场合，结合实际情况选择最合适的网格简化算法。

为什么划分网格前要简化模型如果把FEA分析看作一个黑箱，我们赋予一定的条件然后输入，然后FEA给我们计算输出结果。

这里面有个简单的道理就是：无论多么好的程序，它分析结果的好坏也要依赖于输入数据的精度，无法使结果以高于输入数据的精度输出，也就是说，把形状完整地输入的话是最好的。

把形状完整地划分，理论上如果每个单元都通过检查（单元质量的检查后续会讲解到），那么结果应该是最好的。

但现实却不是这样，这个前面我们也提到过。

要考虑这两个方面：1.如果不简化模型，要适应模型那些微小细节，就需要划分尽量小的单元（而且有时候不一定能成功），而单元越小，计算机求解时间越长，有时候甚至导致计算机内存爆满而死机。

如果模型本身又很大，网格数量可能就会是天文数字。

2.微小细节的地方，网格质量往往不怎么好，如果强行求解，求得的结果收敛性可能很差，准确度反而不好。

关于第1点，这里补充说明一下，一般计算机的求解时间随着单元数量的增加而呈指数函数增加。

我们来做个假设，假设100000个单元情况下，计算时间为1s：那么当单元数量为1000000时，带入可得计算时间大约为8103s （135min），这是非常耗时的，而且你的电脑很可能在计算中崩溃（软件求解时，会把临时数据存到C盘，数据量会随着计算时间的增加而不断积累，几个G，甚至几十个G的数据量很正常）所以，在划分网格前进行模型的简化是非常必要的，特别是有很多微小细节的模型。

如下图所示的小孔和小圆角等。

如果不简化模型，划分单元后就会这样:这些单元往往形状扭曲，很难通过软件的单元质量检查，如果要通过检查，需要把单元划分的特别小，而且往往也不一定行得通。

那么可能有人要问了：我需要做哪些简化？一般需要对模型进行这4种类型的简化：（1）对结构特性没有太大影响的小孔（通孔，填料槽等等）（2）对结构特性没有太大影响的小圆角（3）可以合并到一起的小平面（4）小的边缘上面提到的这些在简化后，不会对结果有什么影响。

三角网格模型的简化技术及多细节层次模型的开题报告简化技术：三角网格模型的简化技术是一种减少模型复杂度的方法，目的是在保持模型外形和重要细节不变的情况下，减少模型的多边形数目，从而提高模型的性能、交互性和渲染速度。

常用的简化技术包括：1. 前后摄像面简化法：根据模型在不同距离下显示的大小及显示的细节程度，设置模型在不同距离下的多边形数。

2. 边界流距离算法：根据模型边界流的距离和流量来选择保留哪些多边形。

3. 误差度量算法：根据测量误差来选择保留哪些多边形。

4. 泊松重构简化：利用网格细化的方法对原来的三角网格重新构建，达到减少面数和保留细节的效果。

5. 聚类简化：选取重心和质心等简化技术选取的聚类算法，将相邻或者相似的面进行聚类，保留少数的多边形反映出原来的几何形状。

多细节层次模型：多细节层次模型是一个在现实时间内有效地演示不同细节层次的方法，由多个不同细节层次的模型组成，每个模型都可以在不同细节层次下显示。

例如，我们可以在近距离观看时显示高分辨率的模型，而在远距离观看时显示低分辨率的模型，以兼顾模型的视觉效果和性能。

多细节层次模型的构建方法通常包括以下步骤：1. 高分辨率模型的建立：使用高分辨率多边形网格（如典型的三角面片网格）构建高分辨率模型。

2. 建立低分辨率模型：使用简化技术对高分辨率模型进行简化，以创建低分辨率模型。

3. 构建模型的多个细节模型：对模型不同的细节进行提炼，如对小的凸起、凹口等细节个体的提取，以创建不同层次的模型。

4. 细节层次的创建：a. 首先，从高分辨率模型中创建一系列低解析度的简化版本（例如，使用误差度分配算法）。

b. 然后，为每个分辨率级别生成相应大小和复杂度的三角面片网格。

c. 最后，在每个分辨率级别上，被重用的面片及其细节信息被重新计算和记录。

以上是多细节层次模型的研究方向，后续研究还需要加强多细节层次模型各层次之间的转换方法、应用方式、细节目标定制化方法等等方面的深入研究。