多边形模型简化算法综述

1943ds max 5标准教程第8章多边形建模不管是否为游戏建模，优化模型并得到正确的细节都是成功产品的关键。

模型中不需要的细节也将增加渲染时间。

模型中使用多少细节是合适的呢？这就是建模的艺术性所在，人眼的经验在这里起着重要作用。

如果角色在背景中快速奔跑，或者喷气飞机在高高的天空快速飞过，那么这样的模型就不需要太多的细节。

8.1 3ds max的表面在3ds max中建模的时候，可以选择如下三种表面形式之一：网格（Meshes）；Bezier面片（Patches）；NURBS（不均匀有理B样条）。

网格最简单的网格是由空间3个离散点定义的面。

尽管它很简单，但的确是3ds max中复杂网格的基础。

本章后面的部分将介绍网格的各个部分，并详细讨论如何处理网格。

面片当给对象应用Edit Patch编辑修改器或者将它们转换成Editable Patch对象时，3ds max 将几何体转换成一组独立的面片。

每个面片由连接边界的3到4个点组成，这些点可定义一个表面。

NURBS术语NURBS代表Non-Uniform Rational B-Splines（不均匀有理B样条）：Non-Uniform（不均匀）意味着可以给对象上的控制点不同的影响，从而产生不规则的表面；Rational（有理）意味着代表曲线或者表面的等式被表示成两个多项式的比，而不是简单的求和多项式。

有理函数可以很好地表示诸如圆锥、球等重要曲线和曲面模型；B-spline (Basis spline，基本样条线)是一个由三个或者多个控制点定义的样条线。

这些点不在样条线上，与使用Line或者其它标准二维图形工具创建的样条线不同。

后者创建的是Bezier曲线，它是B- splines的一个特殊形式。

第8章多边形建模195使用NURBS就可以用数学定义创建精确的表面。

许多现代的汽车设计都是基于NURBS 来创建光滑和流线型的表面。

8.2 对象和次对象3ds max的所有场景都是建立在对象的基础上，每个对象又由一些次对象组成。

多边形生成合并及布尔运算算法研究
近些年来,随着GIS、计算机辅助设计、三维物体表面重建、医学或卫星图像数据处理等领域的发展,多边形的相关运算越来越重要。

多边形的相关运算可大致分为生成、合并及布尔运算,是计算几何中的几个重要的问题。

本文对多边形相关的算法进行了深入细致的研究。

大致分为四个部分:多边形合并算法、线段集生成简单多边形算法、多边形的三角剖分以及多边形布尔运算算法。

主要目的分为两个,一个是简化算法过程,降低时间复杂度,另一个是缩短连接线长度,在实际应用方面可降低成本。

1.给出的多边形合并算法是将两个不相交多边形连接成一条回路。

该算法通过删除多边形两侧距离较短的点,并将剩余顶点构成一个新的多边形,然后对新多边形进行Delaunay三角剖分,以Delaunay边作为对角线构成四边形,找到四边形的边长增值最小的连接点与的对应点,删除相应边,得到具有最小长度的回路,降低了算法的时间复杂度。

2.给出了线段集生成简单多边形算法,首先逐层计算线段集的凸壳,为了缩短连接线段长度和将这些凸壳根据Delaunay三角剖分选取最近点或次最近点改变成简单多边形,然后计算多边形
之间的交点并删除,最后将这些简单多边形合并成一个简单多边形。

对算法进行了分析,给出了时间复杂度。

3.给出了多边形布尔运算算法。

本文算法先根据多边形链求交算法计算出交点,顺时针遍历多边形,不考虑交点对方向的改变,之后根据交点与端点构造出的新多边形中边的方向进行分类,根据求解并、交、差的规则计算出两个多边形的交集、并集和差集。

多边形收缩算法多边形收缩算法，简单来说就是把一个多边形按照一定的规则给变小喽。

你想啊，就像把一个大大的图形慢慢往中心缩。

比如说，咱们有一个很不规则的多边形，可能边边弯弯绕绕的，这个算法就像一个魔法，让这个多边形的每条边都往里面挪一挪。

那这个算法是怎么做到的呢？这里面可大有学问。

一种常见的做法是从多边形的顶点入手。

我们可以想象每个顶点就像一个小钉子，固定着多边形的形状。

当要收缩的时候呢，就把这些小钉子往中心拽一拽。

不过这拽也不是随便拽的哦。

要是拽得太猛或者太随意，那多边形可就变形得不成样子啦。

比如说一个五边形，它的五个顶点都有自己的位置。

我们要计算每个顶点到多边形中心的距离，这个中心可不是随随便便找个点就行的。

可能要通过一些数学方法，像把所有顶点的坐标加起来再除以顶点的个数之类的方法来找到这个中心。

然后呢，根据这个距离和一定的比例，把顶点往中心移动一点点。

在这个过程中，还有很多细节要考虑呢。

就像走钢丝一样，要小心翼翼。

比如说，如果多边形有凹进去的部分，那在收缩的时候就更要注意啦。

不能让这个凹进去的部分变得更奇怪或者消失不见。

这就需要更复杂的计算啦。

我们可能要分别判断每个顶点的情况，看看它周围的边是怎么连接的，再决定这个顶点到底要往中心移动多少。

而且呀，这个算法在很多地方都有用处。

在游戏开发里，你知道吧，很多游戏里的地图或者角色的形状可能就是多边形。

要是想让这个地图或者角色变小一点，就可以用到多边形收缩算法啦。

还有在图形处理软件里，如果要对一个多边形的图案进行缩放或者变形，这个算法也能派上大用场呢。

另外呢，多边形收缩算法也不是只有一种实现方式。

不同的人可能根据不同的需求想出不同的办法。

有的可能更注重速度，希望这个算法能快速地把多边形收缩起来。

那他们可能会采用一些比较简单直接的计算方法，虽然可能不是那么精确，但是速度快呀。

而有的呢，就像那些完美主义者，他们想要让收缩后的多边形看起来特别的整齐、美观，那就会采用更复杂、更精确的计算方式，可能要考虑更多的因素，像多边形的角度啊，边的长度比例啊之类的。

计算机硬件绘图一直在高速的发展，但是仍然不能满足3D场景的实时绘制。

在研究较大规模的可视化模拟系统时，由于3D场景中的模型比较多而且结构比较复杂，如果内存容量无法满足，则不得不牺牲时间进行存储交换。

为了获得高效和理想的视觉效果和计算机处理的速度，需要采用一种技术需要对场景中的模型进行有效的处理。

细节层次模型LOD(Level of Detail)方法就是从软件上提高计算机的绘图速度，改善现实的效果。

该方法由Clarknl于1976年提出,他认为当物体覆盖屏幕较小区域时，可以使用该物体描述较粗的模型，并给出一个用于可见面判断算法的几何层次模型,以便对复杂场景进行快速的绘制。

在场景的动态显示中，当视点距离某一物体很近时，它的图像在屏幕上占据较多的像素,而当视点距离它很远时，图像在屏幕上占据很少的像素，甚至是一个像素，在这种情况下用大量的三角形网格去精确的表示物体已经没有必要,可以适当合并一些三角形，而不损失画面的视觉效果。

这样即保证场景的视觉效果，又能提高场景的绘制帧速，改善系统的实时性。

1、LOD模型简化介绍LOD技术大多数情况下用于简化多边形几何模型，目前在模型简化的研究中，生成层次LOD的方法主要有:细分法、采样法和删减法等。

细分法。

细分法(Refinement)用非常简单的基模型表示初始模型，然后迭代细分基模型，每一步向模型的局部区域增加越来越多的细节，直到细节的模型满足用户定义的误差要求。

采样法。

采样法(Sampling)通过随机抽取一些点来初始化多边形模型,通过较少的多边形数重建初始模型且满足采样点处的误差估计，用户可以控制采样点数,但不能控制最终近似的初始多边形模型。

删减法。

删减法(Decimation)主要通过几何移去模型单元来简化。

几何移去包括:顶点删除、边折叠、边压缩法和三角形删减等。

是应用于那些可以用层次结构来表示的模型。

利用这些基本操作，只要确定每次操作给网格场景带来的误差计算，用这个误差代价计算方法来计算。

一种基于边折叠的多边形网格简化算法
王海滨;阮秋琦
【期刊名称】《铁道学报》
【年(卷),期】2000(022)003
【摘要】虚拟现实的真实感限时图形生成中加速技术十分关键,细节层次模型(LOD)在实时绘制复杂场景中得到了广泛应用.本文介绍了一种基于边折叠的多边形网格简化算法,该算法能够有效地减少模型的多边形数,算法实现简单而且速度快.最后给出了应用实例说明其优点.
【总页数】4页(P52-55)
【作者】王海滨;阮秋琦
【作者单位】北方交通大学,信息科学研究所,北京,100044;北方交通大学,信息科学研究所,北京,100044
【正文语种】中文
【中图分类】TP391
【相关文献】
1.一种面积加权的半边折叠网格简化算法及其递进网格构造 [J], 刘焕敏;杨克俭;王玉华
2.一种边折叠三角网格简化算法 [J], 杜晓晖;尹宝才;孔德慧
3.一种改进的基于三角形折叠的网格简化算法 [J], 孙永辉;姜昱明
4.一种新的边折叠网格模型简化算法 [J], 王继东;张芸;杨斌
5.基于LOD的多边形网格简化算法的优化 [J], 郭海儒;刘沛骞;袁玲玲
因版权原因，仅展示原文概要，查看原文内容请购买。

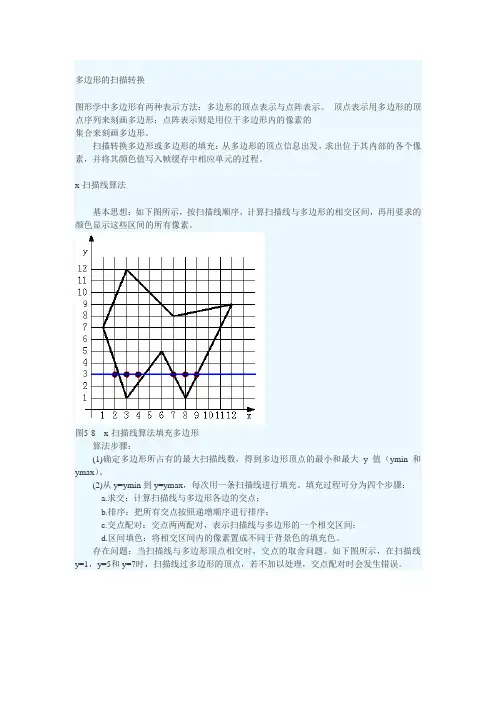
多边形的扫描转换图形学中多边形有两种表示方法：多边形的顶点表示与点阵表示。

顶点表示用多边形的顶点序列来刻画多边形；点阵表示则是用位于多边形内的像素的集合来刻画多边形。

扫描转换多边形或多边形的填充：从多边形的顶点信息出发，求出位于其内部的各个像素，并将其颜色值写入帧缓存中相应单元的过程。

x-扫描线算法基本思想：如下图所示，按扫描线顺序，计算扫描线与多边形的相交区间，再用要求的颜色显示这些区间的所有像素。

图5-8 x-扫描线算法填充多边形算法步骤：(1)确定多边形所占有的最大扫描线数，得到多边形顶点的最小和最大y值（ymin和ymax）。

(2)从y=ymin到y=ymax，每次用一条扫描线进行填充。

填充过程可分为四个步骤：a.求交：计算扫描线与多边形各边的交点；b.排序：把所有交点按照递增顺序进行排序；c.交点配对：交点两两配对，表示扫描线与多边形的一个相交区间；d.区间填色：将相交区间内的像素置成不同于背景色的填充色。

存在问题：当扫描线与多边形顶点相交时，交点的取舍问题。

如下图所示，在扫描线y=1，y=5和y=7时，扫描线过多边形的顶点，若不加以处理，交点配对时会发生错误。

图5-9 与多边形相交的交点的处理解决方法：当扫描线与多边形的顶点相交时，若共享顶点的两条边分别落在扫描线的两边，交点只算一个；若共享顶点的两条边在扫描线的同一边，这时交点作为零个或两个。

实际处理时，只要检查顶点的两条边的另外两个端点的Y值，两个Y值中大于交点Y值的个数是0，1，2，来决定取0，1，2个交点。

改进的有效边表算法由于x-扫描线算法在处理每条扫描线时，需要与多边形所有的边求交，效率很低，因此需要加以改进，形成改进的有效边表算法。

改进原理：(1)处理一条扫描线时，仅对有效边求交。

(2)利用扫描线的连贯性，即当前扫描线与各边的交点顺序与下一条扫描线与各边的交点顺序很可能相同或非常相似。

(3)利用多边形边的连贯性，即当某条边与当前扫描线相交时，它很可能也与下一条扫描线也相交：若边的直线斜率为k，这样边与两条相邻扫描线的交点有如下关系：xi+1=xi+1/k。

多边形收缩填充算法 一提到“多边形收缩填充算法”，乍一听是不是有点绕？别担心，咱们慢慢聊。其实就是一门让复杂形状变得更有趣、更紧凑的技术，它听起来挺高大上，但其实背后的原理比我们想象的简单。咱们可以把它想象成给一个形状穿上“紧身衣”，让它收得更小、更贴合，同时保持原来的轮廓。不信？咱们就来一起看看这个有趣的小家伙是怎么工作的。 一、什么是多边形收缩填充？ 这个算法其实并没有大家想象中的那么难懂。就像你给孩子画个简单的多边形，可能是三角形、五边形或者七边形，都是有固定角度和边的。如果你想让这个多边形变得更小，收缩一点点，让它看起来更紧凑，但又不改变它的形状怎么办呢？多边形收缩填充就是这么一种方式。简单来说，就是将多边形的每一条边缩进一定的距离，然后再填充中间的空白区域。 比如你画了一个正方形，如果你把它的每条边都往中心缩一点，这样就会得到一个新的正方形，但它比原来小，形状没变，大小却变了。然后你再把这个缩小的正方形的空白部分填充上色，看起来是不是很酷？这个过程其实就跟我们常见的“做减法”差不多，往内收缩，把多余的部分去掉，让形状更精炼。想象一下，如果你每次都能这样收缩形状，最后你就能得到各种形状的小版本，既不浪费空间，也不让图形变得乱七八糟。 二、它是怎么填充的呢？ 说到填充，这可不是简单的涂色，得好好讲讲这背后的技巧。毕竟，你想象一下，如果你随便涂色，结果可能就成了一堆五颜六色的混乱图案。多边形收缩填充算法的填充过程其实是要把“缩小”的区域合理地填满，不能让它看起来空荡荡的。你可以想象一 下，咱们常见的“瓷砖铺地”图案，每一块瓷砖都紧密地拼在一起，不留下任何空隙。这个填充的过程和瓷砖铺设有点像，只不过这里是把边界缩小了，然后根据形状的变化来填充。 以三角形为例，假如你把一个大的三角形收缩，原本的空白区域会变成更小的三角形，填充的颜色也要根据新的小三角形的形状来铺设。我们其实就像是在给这个图形找“衣服”一样，找对的颜色和图案来填补空间，使得整个图形看起来既完整又和谐。你也可以理解成，咱们给图形做个“内衣”收紧，填充这些区域，让它看起来更加整洁有序。填充过程不是随便画的，而是要确保收缩后的形状依然能保持原本的风格，填充得当才行。 三、为什么要用这种方法？ 你可能会问，既然图形原本的形状已经完成了，为什么还要去做这些“收缩”和“填充”的操作呢？好吧，这个问题很关键。其实呢，这种方法特别适合用于图形的简化和优化。当我们有复杂的多边形时，想要让它更紧凑，更具实用性，或者在一些工程计算中，我们经常需要将复杂的形状转换成更简单的版本。这时候，收缩填充就能发挥出巨大的作用。 举个例子，你在做地图绘制时，常常会遇到一些非常复杂的地形边界，蜿蜒曲折，难以处理。用这种收缩填充算法，就能将这些边界简化，减少处理的复杂度，让它变得更加容易计算，同时还不失去准确性。更厉害的是，收缩填充还能用在很多不同领域，比如计算机图形学、物理模拟，甚至建筑设计。比如设计师在做建筑外观时，也可以通过这种方式来预览图形的变化，找出最佳的设计方案。收缩填充的好处就是它能帮我们把复杂的东西变得简单，省时省力还不失精致。 四、总结 讲了这么多，我敢打赌你现在对这个“多边形收缩填充算法”已经没那么陌生了吧？它不是什么神秘的东西，也不是复杂到无法理解的黑科技，反而是一个非常实用且富有趣味的工具。通过将多边形的每条边往内收，填充掉中间的空白区域，我们就能把一个大而复杂的图形变得紧凑、有序，甚至还带点艺术感。这种方法在很多领域都有着广泛的应用，从简单的绘图到复杂的工程设计，它的应用价值无可限量。所以，今天我们聊的这些，既是技术，也是艺术，它不仅让图形变得有型，还能让我们在实际操作中感受到不一样的乐趣。 你看看，平时我们都在为图形做加法，设计得越来越复杂，但减少一些冗余，收缩一下，让形状变得简洁明了，反而会让效果更好。就像人生一样，少一些复杂，更多的是精炼和专注。希望你也能通过这个有趣的算法，找到属于自己的“紧身衣”，把复杂的东西都变得简单又美丽！

⼏何算法：点集合构造简单多边形问题：给定平⾯中n个点所组成的集合，将它们连接起来形成⼀条简单的封闭路径。

所谓简单路径，是指边与边⽆交叉。

如下图所⽰10个点组成的简单轮廓：思路：取x坐标最⼤的点A（如果最⼤x坐标的点不⽌⼀个，则取Y坐标最⼩的点），依次计算A点与其余各点的连线与⽔平线之间夹⾓的正切值，然后按照正切值排序，依次连接排序后的各点即组成⼀个简单图形。

原理：其它所有点都在A点的左侧，所有夹⾓的范围为-Pi/2~Pi/2，单调递增函数。

举⼀个例⼦如下：各点坐标与A点的⾓度斜率如下（已经排序好）：x:426.192518536091,y:30.5668629242884,slope:-2.21036105157629x:132.904271903869,y:111.805767306036,slope:0.0233827696146631x:209.153583263584,y:158.396180071121,slope:0.216615047225945x:51.2625493860163,y:271.425922467106,slope:0.409713066051227x:172.80558813494,y:320.363658168522,slope:0.754116336162768x:174.841647802313,y:361.474091434606,slope:0.903935084923323x:262.993097888768,y:306.679940091763,slope:1.03059799172764x:405.520514378101,y:212.478244240618,slope:2.00680658499766x:410.405247491042,y:324.597360433357,slope:4.49064367657446x:459.491329337233,y:104.169257382941,slope:1.79769313486232E+308其中A点为：x:459.491329337233,y:104.169257382941,slope:1.79769313486232E+308下⾯给出具体算法（C#实现）：⼏何点定义，实现IComparable<T>接⼝，按照正切值排序要⽤到：public struct GeometryPoint : IComparable<GeometryPoint>{public GeometryPoint(double x, double y, double slope = double.NaN){this.x = x;this.y = y;this.slope = slope;}private double x;public double X{get { return x; }set { x = value; }}private double y;public double Y{get { return y; }set { y = value; }}private double slope;public double SLOPE{get { return slope; }set { slope = value; }}public int CompareTo(GeometryPoint p){if (this.slope < p.slope){return -1;}else if (this.slope > p.slope){return1;}else{if (this.x == p.x && this.SLOPE == p.SLOPE && this.SLOPE == double.MaxValue){if (this.y == p.y){return0;}else if (this.y < p.y){return1;}else//(this.y > p.y){return -1;}}return0;}}public override string ToString(){return string.Format("x:{0},y:{1},slope:{2}", x, y, slope);}}GeometryPoint 定义简单封闭图形定义，并定义初始化简单封闭图形的⽅法，该⽅法随机产⽣多边形的顶点：public class SimplePolygon{private GeometryPoint[] geometrypoints;public GeometryPoint[] GeometryPoints{get { return geometrypoints; }set { geometrypoints = value; }}public SimplePolygon(){}public void Initialize(int size, double minX, double maxX, double minY, double maxY){if (size <= 0) throw new ArgumentOutOfRangeException();geometrypoints = new GeometryPoint[size];Random rnd = new Random(lisecond);double xRange = maxX - minX;double yRange = maxY - minY;int MaxXPointIndex = 0;//选取x坐标最⼤的点for (int i = 0; i < size; i++){GeometryPoint gp = new GeometryPoint(minX + xRange * rnd.NextDouble(), minY + yRange * rnd.NextDouble());geometrypoints[i] = gp;if (geometrypoints[MaxXPointIndex].X < gp.X)////选取x坐标最⼤的点{MaxXPointIndex = i;}else if (geometrypoints[MaxXPointIndex].X < gp.X && geometrypoints[MaxXPointIndex].Y > gp.Y)//选取x坐标最⼤的点，如果最⼤x坐标点有多个，去y最⼩者 {MaxXPointIndex = i;}}//计算斜率for (int i = 0; i < size; i++){if (i == MaxXPointIndex){geometrypoints[MaxXPointIndex].SLOPE = double.MaxValue;}else{if (geometrypoints[i].X == geometrypoints[MaxXPointIndex].X)//与最⼤x坐标的x相同的点,因为x坐标之差为零，所以取SLOPE最⼤值{geometrypoints[i].SLOPE = double.MaxValue;}else//计算斜率，注意正切函数在-0.5Pi和0.5Pi之间是单调递增的{geometrypoints[i].SLOPE = (geometrypoints[i].Y - geometrypoints[MaxXPointIndex].Y) / (geometrypoints[MaxXPointIndex].X - geometrypoints[i].X);}}}//按照斜率slope排序，取稳定排序⽅法的堆排序。

3DMax中的模型优化和多边形减面技巧在3DMax中，模型优化和多边形减面是非常重要的技巧，它们可以帮助我们提高模型的性能和效率，同时也可以减少渲染和呈现时的工作量。

本文将详细介绍3DMax中的模型优化和多边形减面的步骤和方法。

一、为什么需要模型优化和多边形减面1.1 提高性能：高细节模型往往会占用较多的计算资源和内存，造成渲染时的延迟和卡顿。

通过模型优化和多边形减面可以减少模型的复杂度，提高渲染效率和性能。

1.2 加快制作流程：模型优化和多边形减面可以简化模型的结构和减少不必要的细节，从而减少模型的制作和修改时间，提高制作效率。

1.3 减少渲染和呈现工作量：高细节模型需要更长时间进行渲染和呈现，通过模型优化和多边形减面可以减少渲染和呈现的时间和工作量。

二、模型优化的步骤和方法2.1 移除隐藏面：隐藏面是指在模型中不可见的面，移除它们可以减少不必要的面数，提高模型的性能。

在3DMax中，选择模型，点击“显示面”选项并选择“隐藏的面”，然后按下Delete键即可移除隐藏面。

2.2 合并顶点：模型中的一些顶点可能非常接近或者重合，通过合并这些顶点可以减少模型的顶点数量。

在3DMax中，选择模型，进入编辑模式，选择顶点模式，在合并选项中选择“通过距离合并”，设置适当的合并距离，点击合并按钮即可合并顶点。

2.3 移除不必要的边和面：通过删除模型中的不必要的边和面，可以进一步减少模型的复杂度和面数。

在3DMax中，选择模型，进入编辑模式，选择边或面，点击Delete键即可删除不必要的边和面。

三、多边形减面的步骤和方法3.1 使用多边形减面工具：3DMax中提供了多边形减面工具，可以帮助我们快速减少模型的多边形数量。

首先选择模型，进入编辑模式，在“减面器”选项中选择“多边形减面”，然后调整减面器的参数，如减面比例、是否保持边界等，点击应用即可进行多边形减面。

3.2 手动减面：除了多边形减面工具，我们还可以手动减面模型。

多边形建模原理
多边形建模是一种三维建模技术，它通过将平面多边形组合在一起来创建三维形状。

其原理如下：
1.多边形定义：多边形是由一组有序的顶点和边组成的平面图形。

2.多边形组合：通过将多个平面多边形组合在一起，可以创建出各种复杂的三维形状。

3.三角剖分：由于计算机只能处理三角形，因此在多边形建模中，需要将多边形划分为三角形，这个过程叫做三角剖分。

4.网格建模：多边形建模中的三角形可以组成一个网格，每个三角形可以称为一个面片。

通过调整面片的大小和形状，可以创建出不同的三维形状。

5.优化模型：在建模过程中，需要考虑模型的细节和效率。

可以通过添加细节和优化三角形的数量来提高模型的质量和性能。

6.渲染：最后，将建模完成的三维模型渲染成二维图像或动画，以展示其外观和运动。

离散点拟合多边形-概述说明以及解释1.引言1.1 概述:在现实世界中，我们经常会遇到需要将一组散点数据拟合成一个多边形的情况。

离散点拟合多边形的目的在于找到最佳的多边形形状，使其能够最好地描述给定的数据点集，并且具有良好的拟合性能。

本文将介绍离散点拟合的基本概念和多边形拟合的方法，讨论在实际应用中如何选择合适的拟合方法并应用到不同的场景中。

同时，我们也将讨论多边形拟合在工程、地理、图像处理等领域的具体应用，以及其在各个领域中的优势和局限性。

通过学习离散点拟合多边形的方法和应用，读者将能够更好地理解和运用这一技术，为实际问题的解决提供新的思路和方法。

1.2 文章结构本文主要分为三个部分：引言、正文和结论。

在引言部分，将会对离散点拟合多边形这一主题进行概述，介绍文章的结构和目的，为读者提供一个整体的把握。

在正文部分，将详细介绍离散点拟合的基本概念和原理，探讨多边形拟合的方法和技术，同时探讨多边形拟合在实际应用中的场景和意义。

最后在结论部分，将对整篇文章进行总结，展望未来的研究方向，并提出一些结论性的观点，为读者提供一个完整的知识体系。

1.3 目的本文旨在探讨离散点拟合多边形的方法和应用，通过对多边形拟合方法的介绍和应用场景的分析，希望读者能够了解如何利用离散点数据进行多边形拟合，并从中获得实践经验和启发。

同时，通过研究离散点拟合多边形的过程，可以进一步探讨数学模型的建立和优化方法，在实际问题中得到更好的应用和解决方案。

最终达到在实际工程和科学研究中更好地利用离散点数据进行多边形拟合的目的。

2.正文2.1 离散点拟合在数据分析与处理领域中，离散数据点的拟合是一项常见且重要的任务。

离散点拟合是指通过一定的数学模型或算法，对给定的离散数据点进行拟合，从而得到一个能够较好描述数据特征的曲线或曲面。

离散点拟合的目的是希望通过拟合得到的模型能够准确地反映数据的整体特征，同时能够用于预测未知数据点的数值或趋势。

在离散点拟合的过程中，常用的方法包括线性拟合、多项式拟合、最小二乘拟合等。

多边形分割算法一、引言多边形分割算法是计算机图形学中的一个重要问题。

在实际应用中，多边形分割算法被广泛应用于计算机游戏、建筑设计、CAD等领域。

本文将介绍多边形分割的基本概念和常见算法。

二、多边形分割基本概念1. 多边形多边形是由若干个线段组成的封闭图形。

每条线段称为多边形的一条边，相邻两条边之间的夹角称为内角。

多边形可以分为凸多边形和凹多边形两种。

2. 多边形分割将一个凸或凹多边形划分成若干个不相交的子多边形，使得每个子多边形都是凸多边形，这个过程就称为多边形分割。

3. 三角剖分三角剖分是指将一个复杂的凸或凹多边形划分成若干个三角形。

三角剖分是一种特殊的多边形分割方法，它可以使得每个子图元（三角形单元）面积最小且相互之间没有重叠部分。

三、常见的多变性分割算法1. 三角剖分法三角剖分是最常见的多边形分割算法，它将多边形划分成若干个三角形。

三角剖分有很多种方法，如Delaunay三角剖分、Ear Clipping Triangulation等。

2. 对角线交换法对角线交换法是一种将凸多边形划分为若干个凸子多边形的算法。

该算法首先选择一个顶点，然后从该点开始依次连接其他顶点，如果连接的线段不在多边形内部，则将其作为对角线，将多边形划分为两个子多边形。

接下来再对每个子多边形递归进行划分。

3. 梯形切割法梯形切割法是一种利用梯形进行切割的算法。

该算法首先将多边形按照从上到下的顺序排序，然后依次连接相邻两条线段所在的梯形的上底和下底，直到所有的梯形都被覆盖。

这样就可以将凸或凹多边形划分为若干个凸子多边形。

4. 空间扫描线算法空间扫描线算法是一种基于扫描线的算法。

该算法首先将多边形按照从上到下的顺序排序，然后从上到下依次扫描每一条水平线段，同时记录当前扫描线段与多边形相交的所有线段。

当扫描到某个顶点时，如果该点是凸顶点，则将其加入划分结果中，并删除与该顶点相邻的所有线段；如果该点是凹顶点，则选择与该点相邻的两条线段中跨越最小角度的一条作为对角线，并将多边形划分为两个子多边形。

多边形剖分问题的数学算法设计与优化多边形剖分问题是计算几何学中的一个经典问题，旨在将一个给定的多边形划分为一组不相交的三角形。

这个问题在许多应用领域都有重要的意义，比如计算机图形学、地理信息系统等。

本文将介绍多边形剖分问题的数学算法设计与优化。

一、问题描述给定一个简单多边形P，即没有自交的多边形，我们的目标是将其剖分为一组不相交的三角形。

剖分的结果应满足以下两个条件：1. 三角形的顶点都是多边形的顶点。

2. 三角形的边都是多边形的边或者剖分线段。

二、朴素算法朴素算法是最简单直观的解决方法，其思路是逐步添加剖分线段，直到将多边形剖分为三角形为止。

具体步骤如下：1. 选择一个顶点作为起始点。

2. 选择下一个顶点，构成一条线段与多边形的边相交。

3. 如果该线段与多边形的其他边不相交，则将其加入剖分结果。

4. 如果该线段与多边形的其他边相交，则选择一个交点作为新的起始点，重复步骤2和3，直到多边形被完全剖分。

朴素算法的时间复杂度为O(n^3)，其中n为多边形的顶点数。

虽然简单易懂，但对于大规模多边形的剖分效率较低。

三、三角剖分算法三角剖分算法是一种高效的多边形剖分方法，其核心思想是将多边形划分为一组互不相交的三角形。

常见的三角剖分算法有Delaunay三角剖分、Ear Clipping等。

1. Delaunay三角剖分Delaunay三角剖分是一种基于点集的三角剖分算法，其思路是将多边形的顶点作为点集，通过连接这些点来构建三角形。

Delaunay三角剖分具有以下特点：- 任意两个三角形的外接圆不相交。

- 最小化所有三角形的最小角度。

Delaunay三角剖分算法的时间复杂度为O(nlogn)，其中n为多边形的顶点数。

该算法在计算机图形学中被广泛应用，可以高效地生成复杂多边形的三角剖分结果。

2. Ear ClippingEar Clipping算法是一种基于边的三角剖分算法，其思路是逐步剪除多边形的耳朵。

具体步骤如下：- 选择一个顶点，将其与相邻的两个顶点构成一条边。