三角函数公式大全表格初中数学

鄙视下载资料还要财富值的！
一：指数函数
二：对数函数
三：指数函数与对数函数有什么关系?（关于y=x 对称）
x
y 2=x
y 3=x
y ⎪⎭
⎫ ⎝⎛=21x
y ⎪⎭
⎫ ⎝⎛=31x
y 2log =x
y 2
1log =x
y 3log =x
y 3
1log =x
y 2=x
y =x
y 2log =
二、基本初等函数及其图像
1
2
3
，奇函数
无界，周期为余割函数
，偶函数无界，周期为正割函数，奇函数无界，周期为余切函数，奇函数无界，周期为正切函数，偶函数有界，周期为余弦函数，奇函数有界，周期为正弦函数性质
表达式名称ππππππ2csc 2sec cot tan 2cos 2sin x
y x y x y x y x y x y ======)
R (sin ∈=x x y 的图象)
R (cos ∈=x x y 的图象tan (π0.5π)
y x x k =≠+的图像
4
cot (π)
y x x k =≠的图像)
0()
(cot arc 22)(arctan ]0[]11[arccos 22]11[arcsin ππππππ，，反余切函数
，，反正切函数，，反余弦函数，，反正弦函数值域定义域表达式名称∞+-∞=⎪⎭⎫ ⎝⎛-∞+-∞=-=⎥⎦⎤
⎢⎣⎡--=x
y x y x y x y。

(完整版)三角函数公式表1. 正弦函数 (sin):定义：正弦函数是直角三角形中对边与斜边的比值。

公式：sin(θ) = 对边 / 斜边范围：1 ≤ sin(θ) ≤ 1特殊值：sin(0°) = 0, sin(30°) = 1/2, sin(45°) = √2/2, sin(60°) = √3/2, sin(90°) = 12. 余弦函数 (cos):定义：余弦函数是直角三角形中邻边与斜边的比值。

公式：cos(θ) = 邻边 / 斜边范围：1 ≤ cos(θ) ≤ 1特殊值：cos(0°) = 1, cos(30°) = √3/2, cos(45°) = √2/2, cos(60°) = 1/2, cos(90°) = 03. 正切函数 (tan):定义：正切函数是直角三角形中对边与邻边的比值。

公式：tan(θ) = 对边 / 邻边范围：tan(θ) 可以取任意实数值特殊值：tan(0°) = 0, tan(30°) = 1/√3, tan(45°) = 1, tan(60°)= √3, tan(90°) 不存在（无穷大）4. 余切函数 (cot):定义：余切函数是直角三角形中邻边与对边的比值。

公式：cot(θ) = 邻边 / 对边范围：cot(θ) 可以取任意实数值特殊值：cot(0°) 不存在（无穷大）, cot(30°) = √3, cot(45°) = 1, cot(60°) = 1/√3, cot(90°) = 05. 正割函数 (sec):定义：正割函数是直角三角形中斜边与邻边的比值。

公式：sec(θ)= 1 / cos(θ)范围：sec(θ) 可以取任意实数值特殊值：sec(0°) = 1, sec(30°) = 2, sec(45°) = √2, sec(60°) = 2/√3, sec(90°) 不存在（无穷大）6. 余割函数 (csc):定义：余割函数是直角三角形中斜边与对边的比值。

初中三角函数值表2初中三角函数值表特殊角三角函数值sin0=0 sin30=0.5 sin45=0.7071=22 sin60=23=0.866sin90=1 cos0=1 cos30=23=0.866 cos45=22=0.70cos60=0.5 cos90=0 tan0=0 tan30=33=0.577 tan45=1 tan60=3=1.732 tan90=无 cot0=无cot30=3=1.732 cot45=1 cot60=33=0.577 cot90=0（2）0°～90°的任意角的三角函数值，查三角函数表。

（见下）（3）锐角三角函数值的变化情况（i ）锐角三角函数值都是正值（ii ）当角度在0°～90°间变化时，正弦值随着角度的增大（或减小）而增大（或减小）余弦值随着角度的增大（或减小）而减小（或增大）正切值随着角度的增大（或减小）而增大（或减小）余切值随着角度的增大（或减小）而减小（或增大）（iii）当角度在0°≤α≤90°间变化时，0≤sinα≤1, 1≥cosα≥0,当角度在0°<α<90°间变化时，tanα>0, cotα>0.附：三角函数值表sin0=0,sin15=（√6-√2)/4 ,sin30=1/2,sin45=√2/2,sin60=√3/2,sin75=(√6+√2)/2 ,sin90=1,sin105=√2/2*(√3/2+1/2)sin120=√3/2sin135=√2/23sin150=1/2sin165=（√6-√2)/4sin180=0sin270=-1sin360=04sin1=0.01745 sin2=0.034899 sin3=0.052335sin4=0.069756sin5=0.087155sin6=0.104528sin7=0.121869sin8=0.139173sin9=0.156434sin10=0.17364sin11=0.19080sin12=0.20791sin13=0.22495sin14=0.24192sin15=0.25881sin16=0.27563sin17=0.29237sin18=0.30901sin19=0.32556sin20=0.34202sin21=0.35836sin22=0.374605sin24=0.40673sin25=0.42261sin26=0.43837 sin27=0.45399sin28=0.46947 sin29=0.48480sin30=0.49999sin31=0.51503sin32=0.52991sin33=0.54463sin34=0.55919sin35=0.57357sin36=0.58778sin37=0.60181sin38=0.61566sin39=0.62932sin40=0.64278sin41=0.65605sin42=0.66913sin43=0.68199sin44=0.69465sin45=0.70710sin46=0.71933 sin47=0.73135sin48=0.74314sin49=0.75470sin50=0.76604sin51=0.77714sin52=0.788016sin54=0.80901sin55=0.81915sin56=0.82903sin57=0.83867sin58=0.84804sin59=0.85716sin60=0.86602sin61=0.87461sin62=0.88294sin63=0.89100sin64=0.89879sin65=0.90630sin66=0.91354sin67=0.92050sin68=0.92718sin69=0.93358sin70=0.93969sin71=0.94551sin72=0.95105sin73=0.95630sin74=0.96126sin75=0.96592sin76=0.970297sin78=0.97814sin79=0.98162sin80=0.98480sin81=0.98768sin82=0.99026sin83=0.99254sin84=0.99452sin85=0.99619sin86=0.99756sin87=0.99862sin88=0.99939sin89=0.99984sin90=1cos1=0.99984cos2=0.99939cos3=0.99862cos4=0.99756cos5=0.99619cos6=0.99452cos7=0.99254cos8=0.99026cos9=0.98768cos10=0.9848cos11=0.98168cos12=0.97814cos13=0.9743cos14=0.9702cos15=0.9659cos16=0.9612cos17=0.9563cos18=0.9510cos19=0.9455cos20=0.9396cos21=0.9335cos22=0.9271cos23=0.9205cos24=0.9135cos25=0.9063cos26=0.8987cos27=0.8910cos28=0.8829cos29=0.8746cos30=0.8660cos31=0.8571cos32=0.8480cos33=0.8386cos34=0.8290cos35=0.8191cos36=0.8090cos37=0.7986cos38=0.78809cos39=0.7771cos40=0.7660cos41=0.7547cos42=0.7431cos43=0.7313cos44=0.7193cos45=0.7071cos46=0.6946cos47=0.6819cos48=0.6691cos49=0.6560cos50=0.6427cos51=0.6293 cos52=0.6156 cos53=0.6018 cos54=0.5877 cos55=0.5735cos56=0.5592 cos57=0.5446cos58=0.5299cos59=0.5150cos60=0.5000cos61=0.4848cos62=0.4694cos63=0.4539cos64=0.438310cos65=0.4226cos66=0.4067cos67=0.3907cos68=0.3746cos69=0.3583cos70=0.3420cos71=0.3255cos72=0.3090cos73=0.2923cos74=0.2756cos75=0.2588cos76=0.2419cos77=0.2249cos78=0.2079cos79=0.1908cos80=0.1736cos81=0.1564cos82=0.1391cos83=0.1218 cos84=0.1045cos85=0.0871cos86=0.0697311cos87=0.052cos88=0.0348cos89=0.0174cos90=0tan1=0.017455tan2=0.034920tan3=0.052407tan4=0.069926tan5=0.087488tan6=0.105104tan7=0.122784tan8=0.140540tan9=0.158384tan10=0.17632tan11=0.19438tan12=0.21255tan13=0.23086 tan14=0.24932tan15=0.26794tan16=0.28674tan17=0.30573 tan18=0.32491tan19=0.34432tan20=0.36397tan21=0.38386tan22=0.40402tan23=0.42447tan24=0.44522tan25=0.46630tan26=0.48773an27=0.50952tan28=0.5317012tan29=0.55430tan30=0.57735tan31=0.60086tan32=0.62486 tan33=0.64940tan34=0.67450tan35=0.70020tan36=0.72654tan37=0.75355tan38=0.78128tan39=0.80978tan40=0.83909tan41=0.86928tan42=0.90040tan43=0.93251tan44=0.96568tan45=0.99999tan46=1.03553tan47=1.07236tan48=1.11061tan49=1.15036tan50=1.19175tan51=1.23489tan52=1.27994tan53=1.3270413tan54=1.3763tan55=1.42814 tan56=1.48256tan57=1.53986tan58=1.60033tan59=1.66427 tan60=1.73205tan61=1.80404tan62=1.88072tan63=1.96261tan64=2.05030tan65=2.14450tan66=2.24603tan67=2.35585tan68=2.47508tan69=2.60508tan70=2.74747tan71=2.90421tan72=3.07768tan73=3.27085tan74=3.48741tan75=3.73205tan76=4.01078tan77=4.33147tan78=4.70463tan79=5.14455tan80=5.6712814tan81=6.31375tan82=7.11536tan83=8.14434tan84=9.51436tan85=11.4300tan86=14.3006tan87=19.0811tan88=28.6362tan89=57.2899tan90=无取值15。

初中数学三角函数值公式表大全正弦函数值公式表$\\sin 0 = 0$$\\sin \\frac{\\pi}{6} = \\frac{1}{2}$$\\sin \\frac{\\pi}{4} = \\frac{\\sqrt{2}}{2}$ $\\sin \\frac{\\pi}{3} = \\frac{\\sqrt{3}}{2}$ $\\sin \\frac{\\pi}{2} = 1$$\\sin \\pi = 0$$\\sin \\frac{3\\pi}{2} = -1$$\\sin 2\\pi = 0$余弦函数值公式表$\\cos 0 = 1$$\\cos \\frac{\\pi}{6} = \\frac{\\sqrt{3}}{2}$ $\\cos \\frac{\\pi}{4} = \\frac{\\sqrt{2}}{2}$ $\\cos \\frac{\\pi}{3} = \\frac{1}{2}$$\\cos \\frac{\\pi}{2} = 0$$\\cos \\pi = -1$$\\cos \\frac{3\\pi}{2} = 0$$\\cos 2\\pi = 1$正切函数值公式表$\\tan 0 = 0$$\\tan \\frac{\\pi}{6} = \\frac{\\sqrt{3}}{3}$$\\tan \\frac{\\pi}{4} = 1$$\\tan \\frac{\\pi}{3} = \\sqrt{3}$$\\tan \\frac{\\pi}{2}$ 不存在$\\tan \\pi = 0$$\\tan \\frac{3\\pi}{2} = 0$$\\tan 2\\pi = 0$余切函数值公式表$\\cot 0$ 不存在$\\cot \\frac{\\pi}{6} = \\sqrt{3}$$\\cot \\frac{\\pi}{4} = 1$$\\cot \\frac{\\pi}{3} = \\frac{\\sqrt{3}}{3}$ $\\cot \\frac{\\pi}{2} = 0$$\\cot \\pi$ 不存在$\\cot \\frac{3\\pi}{2} = 0$$\\cot 2\\pi = 0$正割函数值公式表$\\sec 0 = 1$$\\sec \\frac{\\pi}{6} = \\frac{2}{\\sqrt{3}}$ $\\sec \\frac{\\pi}{4} = \\sqrt{2}$$\\sec \\frac{\\pi}{3} = 2$$\\sec \\frac{\\pi}{2} = \\infty$$\\sec \\pi = -1$$\\sec \\frac{3\\pi}{2} = \\infty$$\\sec 2\\pi = 1$余割函数值公式表$\\csc 0 = \\infty$$\\csc \\frac{\\pi}{6} = 2$$\\csc \\frac{\\pi}{4} = \\sqrt{2}$$\\csc \\frac{\\pi}{3} = \\frac{2}{\\sqrt{3}}$$\\csc \\frac{\\pi}{2} = 1$$\\csc \\pi = \\infty$$\\csc \\frac{3\\pi}{2} = -\\infty$$\\csc 2\\pi = \\infty$以上是初中数学中常见的三角函数值公式表，通过这些公式可以快速计算各角度下的三角函数值，希望可以帮助大家更好地理解三角函数的性质和应用。

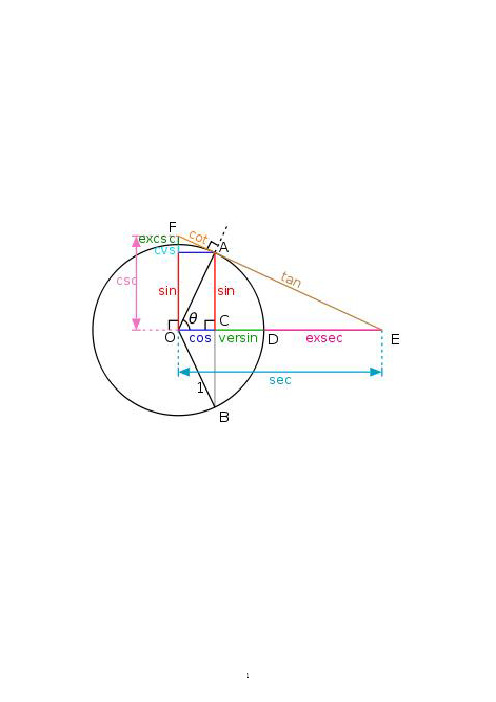
三角函数公式一、任意角的三角函数在角α的终边上任取．．一点),(y x P ,记：22y x r +=， 正弦函数：ry=αsin 余弦函数：r x =αcos 正切函数：x y =αtan余切函数：y x =αcot 正割函数：xr=αsec 余割函数：yr=αcsc 二、同角三角函数的基本关系式六边形记忆法：图形结构“上弦中切下割,左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。

”倒数关系：1csc sin =⋅x x ,1sec cos =⋅x x ，1cot tan =⋅x x 。

商数关系：x x x cos sin tan =，xxx sin cos cot =。

平方关系：1cos sin 22=+x x ，x x 22sec tan 1=+，x x 22csc cot 1=+。

积的关系：sinx=tanx·cosx cosx=sinx·cotx tanx=sinx·secxcotx=cosx·cscx secx=tanx·cscx cscx=secx·cotx三、诱导公式公式一：设α为任意角,终边相同的角的同一三角函数的值相等:sin （2kπ＋α）＝sinα cos（2kπ＋α）＝cosαtan （2kπ＋α）＝tanα cot（2kπ＋α)＝cotα (其中k ∈Z) 公式二：设α为任意角，π＋α的三角函数的值与α的三角函数值之间的关系： sin （π＋α）＝－sinα cos（π＋α）＝－cosα tan （π＋α）＝tanα cot（π＋α）＝cotα公式三：任意角α与－α的三角函数值之间的关系： sin （－α）＝－sinα cos（－α）＝cosα tan(－α）＝－tanα cot（－α）＝－cotα公式四：利用公式二和公式三可以得到π－α与α的三角函数值之间的关系： sin （π－α）＝sinα cos（π－α）＝－cosα tan （π－α）＝－tanα cot(π－α）＝－cotα 公式五：απ-2与α的三角函数值之间的关系:sin （απ-2）＝cosα cos（απ-2）＝sinα tan （απ-2）＝cotα cot（απ-2）＝tanα公式六:απ+2与α的三角函数值之间的关系:sin （απ+2）＝cosα cos（απ+2）＝－sinαtan(απ+2)＝－cotα cot（απ+2）＝－tanα公式七：απ-23与α的三角函数值之间的关系： sin(απ-23）＝－cosα cos（απ-23）＝－sinαtan （απ-23)＝cotα cot（απ-23）＝tanα公式八：απ+23与α的三角函数值之间的关系：sin(απ+23）＝－cosα cos（απ+23）＝sinαtan （απ+23）＝－cotα cot（απ+23）＝－tanα公式九：利用公式一和公式三可以得到2π－α与α的三角函数值之间的关系： sin （2π－α)＝－sinα cos(2π－α）＝cosα tan （2π－α)＝－tanα cot（2π－α）＝－cotα⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值，前面加上一个把α看成．．锐角时原函数值的符号。

三角函数公式表三角函数公式表同角三角函数的基本关系式倒数关系: 商的关系：平方关系：tanα ·cotα＝1sinα ·cscα＝1cosα ·secα＝1 sinα/cosα＝tanα＝secα/cscαcosα/sinα＝cotα＝cscα/secα sin2α＋cos2α＝11＋tan2α＝sec2α1＋cot2α＝csc2α（六边形记忆法：图形结构“上弦中切下割，左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。

”）诱导公式（口诀:奇变偶不变，符号看象限。

）sin（－α）＝－sinαcos（－α）＝cosα tan（－α）＝－tanαcot（－α）＝－cotαsin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝cotαcot（π/2－α）＝tanαsin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotαcot（π/2＋α）＝－tanαsin（π－α）＝sinαcos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－cotαsin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α）＝cotαsin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanαsin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－cotαcot（3π/2＋α）＝－tanαsin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotαsin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanαcot（2kπ＋α）＝cotα(其中k∈Z)两角和与差的三角函数公式万能公式sin（α＋β）＝sinαcosβ＋cosαsinβsin（α－β）＝sinαcosβ－cosαsinβcos（α＋β）＝cosαcosβ－sinαsinβcos（α－β）＝cosαcosβ＋sinαsinβtanα＋tanβtan（α＋β）＝——————1－tanα ·tanβtanα－tanβtan（α－β）＝——————1＋tanα ·tanβ2tan(α/2)sinα＝——————1＋tan2(α/2)1－tan2(α/2)cosα＝——————1＋tan2(α/2)2tan(α/2)tanα＝——————1－tan2(α/2)半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α＝2sinαcosαcos2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2α2tanαtan2α＝—————1－tan2αsin3α＝3sinα－4sin3αcos3α＝4cos3α－3cosα3tanα－tan3αtan3α＝——————1－3tan2α三角函数的和差化积公式三角函数的积化和差公式α＋βα－βsinα＋sinβ＝2sin———·cos———2 2α＋βα－βsinα－sinβ＝2cos———·sin———2 2α＋βα－βcosα＋cosβ＝2cos———·cos———2 2α＋βα－βcosα－cosβ＝－2sin———·sin———2 2 1sinα ·cosβ＝-[sin（α＋β）＋sin（α－β）]21cosα ·sinβ＝-[sin（α＋β）－sin（α－β）]21cosα ·cosβ＝-[cos（α＋β）＋cos（α－β）]21sinα ·sinβ＝— -[cos（α＋β）－cos（α－β）]2化asinα±bcosα为一个角的一个三角函数的形式（辅助角的三角函数的公式集合、函数集合简单逻辑任一x∈A x∈B，记作A BA B，B A A＝BA B＝{x|x∈A，且x∈B}A B＝{x|x∈A，或x∈B}c ard（A B）＝card（A）+card（B）－card（A B）（1）命题原命题若p则q逆命题若q则p否命题若 p则 q逆否命题若 q，则 p（2）四种命题的关系（3）A B，A是B成立的充分条件B A，A是B成立的必要条件A B，A是B成立的充要条件函数的性质指数和对数（1）定义域、值域、对应法则（2）单调性对于任意x1，x2∈D若x1＜x2 f（x1）＜f（x2），称f（x）在D上是增函数若x1＜x2 f（x1）＞f（x2），称f（x）在D上是减函数（3）奇偶性对于函数f（x）的定义域内的任一x，若f（－x）＝f（x），称f （x）是偶函数若f（－x）＝－f（x），称f（x）是奇函数（4）周期性对于函数f（x）的定义域内的任一x，若存在常数T，使得f（x+T）＝f(x)，则称f（x）是周期函数（1）分数指数幂正分数指数幂的意义是负分数指数幂的意义是（2）对数的性质和运算法则loga（MN）＝logaM+logaNlogaMn＝nlogaM（n∈R）指数函数对数函数（1）y＝ax（a＞0，a≠1）叫指数函数（2）x∈R，y＞0图象经过（0，1）a＞1时，x＞0，y＞1；x＜0，0＜y＜10＜a＜1时，x＞0，0＜y＜1；x＜0，y＞1a＞ 1时，y＝ax是增函数0＜a＜1时，y＝ax是减函数（1）y＝logax（a＞0，a≠1）叫对数函数（2）x＞0，y∈R图象经过（1，0）a＞1时，x＞1，y＞0；0＜x＜1，y＜00＜a＜1时，x＞1，y＜0；0＜x＜1，y＞0a＞1时，y＝logax是增函数0＜a＜1时，y＝logax是减函数指数方程和对数方程基本型logaf(x)＝b f（x）＝ab（a＞0，a≠1）同底型logaf（x）＝logag（x） f（x）＝g（x）＞0（a＞0，a≠1）换元型 f（ax）＝0或f (logax)＝0数列数列的基本概念等差数列（1）数列的通项公式an＝f（n）（2）数列的递推公式（3）数列的通项公式与前n项和的关系an+1－an＝dan＝a1+（n－1）da，A，b成等差 2A＝a+bm+n＝k+l am+an＝ak+al等比数列常用求和公式an＝a1qn＿1a，G，b成等比 G2＝abm+n＝k+l aman＝akal不等式不等式的基本性质重要不等式a＞b b＜aa＞b，b＞c a＞ca＞b a+c＞b+ca+b＞c a＞c－ba＞b，c＞d a+c＞b+da＞b，c＞0 ac＞bca＞b，c＜0 ac＜bca＞b＞0，c＞d＞0 ac＜bda＞b＞0 dn＞bn（n∈Z，n＞1）a＞b＞0 ＞（n∈Z，n＞1）（a－b）2≥0a，b∈R a2+b2≥2ab|a|－|b|≤|a±b|≤|a|+|b|证明不等式的基本方法比较法（1）要证明不等式a＞b（或a＜b），只需证明a－b＞0（或a－b＜0＝即可（2）若b＞0，要证a＞b，只需证明，要证a＜b，只需证明综合法综合法就是从已知或已证明过的不等式出发，根据不等式的性质推导出欲证的不等式（由因导果）的方法。

数学三角函数公式表三角函数公式是数学中常用的公式之一，它们描述了三角函数之间的关系和性质。

在数学领域，三角函数是一个重要的研究对象，广泛应用于几何、物理、工程以及其他领域的计算中。

下面将给出一些常见的三角函数公式表。

一、正弦函数（Sine Function）：1.正弦函数的定义域是实数集，其值域是[-1,1]之间的实数。

2.基本关系：- sin(a + b) = sin a * cos b + cos a * sin b- sin(a - b) = sin a * cos b - cos a * sin b- sin(2a) = 2 * sin a * cos a- sin(a) = 2 * sin(a/2) * cos(a/2)二、余弦函数（Cosine Function）：1.余弦函数的定义域是实数集，其值域是[-1,1]之间的实数。

2.基本关系：- cos(a + b) = cos a * cos b - sin a * sin b- cos(a - b) = cos a * cos b + sin a * sin b- cos(2a) = cos^2 a - sin^2 a- cos^2 a + sin^2 a = 1三、正切函数（Tangent Function）：1.正切函数的定义域是实数集，其值域是全体实数。

2.基本关系：- tan(a + b) = (tan a + tan b) / (1 - tan a * tan b)- tan(a - b) = (tan a - tan b) / (1 + tan a * tan b)- tan(2a) = 2 * tan a / (1 - tan^2 a)四、余切函数（Cotangent Function）：1.余切函数的定义域是实数集，其值域是全体实数。

2.基本关系：- cot(a) = 1 / tan(a)五、正割函数（Secant Function）：1.正割函数的定义域是实数集，其值域是(-∞,-1]∪[1,+∞)之间的实数。

初中数学三角函数公式知识点总结三角函数公式表sin是对边比斜边，cos是邻边比斜边，tan是对边比邻边cot邻边比对边。

sin30是二分之一，sin45是二分之根二，sin60是二分之根三。

cos30是二分之根三，cos45是二分之根二，cos60是二分之一tan30是三分之根三，tan45是一，tan60是根三。

cot30是根三，cot45是一，cot60是三分之根三。

（1）互余关系sinA=cos(90°—A)，cosA=sin(90°—A)tanA=cot(90°—A)，cotA=tan(90°—A)（2）平方关系sin2A+cos2A=1（3）倒数关系tanAtan(90°—A)=1（4）弦切关系tanA= sinA/cosA(5)三角函数的增减性当角度在0°~90°之间变化时，（1）正弦值随着角度的增大（或减小）而增大（或减小）（2）余弦值随着角度的增大（或减小）而减小（或增大）（3）正切值随着角度的增大（或减小）而增大（或减小）（4）余切值随着角度的增大（或减小）而减小（或增大）三角函数和差化积公式sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]三角函数积化和差公式sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]三角函数万能公式sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]三角函数半角公式sin^2(α/2)=(1-cosα)/2cos^2(α/2)=(1+cosα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα三角函数三倍角公式sin3α=3sinα-4sin^3(α)cos3α=4cos^3(α)-3cosα三角函数倍角公式sin(2α)=2sinα·cosαcos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) tan(2α)=2tanα/[1-tan^2(α)]三角函数两角和与差公式cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)三倍角公式推导tan3α=sin3α/cos3α=(sin2αcosα+cos2αsinα)/(cos2αcosα-sin2αsinα)=(2sinαcos^2(α)+cos^2(α)sinα-sin^3(α))/(cos^3(α)-cosαsin^2(α)-2sin^2(α)cosα)上下同除以cos^3(α)，得：tan3α=(3tanα-tan^3(α))/(1-3tan^2(α))sin3α=sin(2α+α)=sin2αcosα+cos2αsinα=2sinαcos^2(α)+(1-2sin^2(α))sinα=2sinα-2sin^3(α)+sinα-2sin^3(α)=3sinα-4sin^3(α)cos3α=cos(2α+α)=cos2αcosα-sin2αsinα=(2cos^2(α)-1)cosα-2cosαsin^2(α)=2cos^3(α)-cosα+(2cosα-2cos^3(α))=4cos^3(α)-3cosα即sin3α=3sinα-4sin^3(α)cos3α=4cos^3(α)-3cosα。

(完整版)初中三角函数公式表一、三角函数的基本定义在初中数学中，三角函数主要涉及正弦函数（sin）、余弦函数（cos）和正切函数（tan）。

这些函数与直角三角形的三边长度有着密切的关系。

1. 正弦函数（sin）：正弦函数表示直角三角形中，对应于一个锐角的斜边与斜边与邻边之比。

公式为：sin(θ) = 对边 / 斜边。

2. 余弦函数（cos）：余弦函数表示直角三角形中，对应于一个锐角的邻边与斜边之比。

公式为：cos(θ) = 邻边 / 斜边。

3. 正切函数（tan）：正切函数表示直角三角形中，对应于一个锐角的斜边与邻边之比。

公式为：tan(θ) = 对边 / 邻边。

二、三角函数的相互关系1. 正弦函数和余弦函数的关系：sin(θ) = cos(90° θ)，cos(θ) = sin(90° θ)。

2. 正切函数和余弦函数的关系：tan(θ) = sin(θ) / cos(θ)。

3. 正切函数和正弦函数的关系：tan(θ) = sin(θ) / cos(θ)。

三、三角函数的特殊值1. 0°：sin(0°) = 0，cos(0°) = 1，tan(0°) = 0。

2. 30°：sin(30°) = 1/2，cos(30°) = √3/2，tan(30°) =1/√3。

3. 45°：sin(45°) = √2/2，cos(45°) = √2/2，tan(45°)= 1。

4. 60°：sin(60°) = √3/2，cos(60°) = 1/2，tan(60°) = √3。

5. 90°：sin(90°) = 1，cos(90°) = 0，tan(90°) 无定义。

四、三角函数的周期性三角函数具有周期性，即函数值在一定的周期内会重复出现。

1、角：1、正角、负角、零角：逆时针方向旋转正角,顺时针方向旋转负角,不做任何旋转零角；2、与α终边相同的角,连同角α在内,都可以表示为集合{Z k k ∈⋅+=,360|αββ}3、象限的角：在直角坐标系内,顶点与原点重合,始边与x 轴的非负半轴重合,角的终边落在第几象限,就是第几象限的角；角的终边落在坐标轴上,这个角不属于任何象限;2、弧度制：1、定义：等于半径的弧所对的圆心角叫做1弧度的角,用弧度做单位叫弧度制; 2、度数与弧度数的换算：π=180弧度,1弧度57)180( ≈=π3、弧长公式：r l ||α= α是角的弧度数扇形面积：2||2121r lr S α===3、三角函数1、定义：如图2、各象限的符号：yry x r x xrx y r y ======ααααααcsc cot cos sec tan sin 4、同角三角函数基本关系式１平方关系： ２商数关系： ３倒数关系：1cos sin 22=+αα αααcos sin tan = 1cot tan =αα αα22sec tan 1=+ αααsin cos cot =1csc sin =αα αα22csc cot 1=+ 1sec cos =αα4同角三角函数的常见变形：活用“1” ①、αα22cos 1sin-=, αα2cos 1sin -±=；αα22sin 1cos -=, αα2sin 1cos -±=；②θθθθθθθ2sin 2cos sin sin cos cot tan 22=+=+,αααααααθθ2cot 22sin 2cos 2cos sin sin cos tan cot 22==-=-③ααααα2sin 1cos sin 21)cos (sin 2±=±=±, |cos sin |2sin 1ααα±=±xy+ + __O xy++__ Oαtanxy+ +__O=r αsecαsinαtan αcotcsc5、诱导公式：奇变偶不变,符号看象限公式一： ααααααtan )360tan(cos )360cos(sin )360sin(=︒⋅+=︒⋅+=︒⋅+k k k公式二： 公式三： 公式四： 公式五：ααααααtan )180tan(cos )180cos(sin )180sin(-=-︒-=-︒=-︒ ααααααtan )180tan(cos )180cos(sin )180sin(=+︒-=+︒-=+︒ ααααααtan )tan(cos )cos(sin )sin(-=-=--=- ααααααtan )360tan(cos )360cos(sin )360sin(-=-︒=-︒-=-︒ 补充：ααπααπααπcot )2tan(sin )2cos(cos )2sin(=-=-=- ααπααπααπcot )2tan(sin )2cos(cos )2sin(-=+-=+=+ ααπααπααπcot )23tan(sin )23cos(cos )23sin(=--=--=- ααπααπααπcot )23tan(sin )23cos(cos )23sin(-=+=+-=+6、两角和与差的正弦、余弦、正切 7 .辅角公式 ⎪⎪⎭⎫ ⎝⎛++++=+x b a b x b a a b a xb x a cos sin cos sin 222222 )sin()sin cos cos (sin 2222ϕϕϕ+⋅+=⋅+⋅+=x b a x x b a其中ϕ称为辅助角,ϕ的终边过点),(b a ,ab =ϕtan 多用于研究性质 8、二倍角公式：1、α2S ： αααcos sin 22sin = 2、降次公式：多用于研究性质 α2C ： ααα22sin cos 2cos -= ααα2sin 21cos sin =1cos 2sin 2122-=-=αα 212cos 2122cos 1sin 2+-=-=αααα2T ： ααα2tan 1tan 22tan -= 212cos 2122cos 1cos 2+=+=ααα 3、二倍角公式的常用变形：①、|sin |22cos 1αα=-, |cos |22cos 1αα=+；②、|sin |2cos 2121αα=-, |cos |2cos 2121αα=+③22sin 1cos sin 21cos sin 22244ααααα-=-=+； ααα2cos sin cos 44=-；④半角：2cos 12sin αα-±=,2cos 12cos αα+±=,αααcos 1cos 12tan +-±=ααααcos 1sin sin cos 1+=-=9、三角函数的图象性质1、函数的周期性：①、定义：对于函数fx ,若存在一个非零常数T,当x 取定义域内的每一个值时,都有：fx +T = fx ,那么函数fx 叫周期函数,非零常数T 叫这个函数的周期；②、如果函数fx 的所有周期中存在一个最小的正数,这个最小的正数叫fx 的最小正周期; 2、函数的奇偶性：①、定义：对于函数fx 的定义域内的任意一个x , 都有：f-x= - fx ,则称fx 是奇函数,f-x= fx ,则称fx 是偶函数②、奇函数的图象关于原点对称,偶函数的图象关于y 轴对称； ③、奇函数,偶函数的定义域关于原点对称；x y sin =图象的五个关键点：0,0,2,1,π,0,2,-1,π2,0；π3πx y sin =的对称中心为0,πk ；对称轴是直线2ππ+=k x ； )sin(ϕω+=x A y 的周期ωπ2=T ；x y cos =的对称中心为0,2ππ+k ；对称轴是直线πk x =； )cos(ϕω+=x A y 的周期ωπ2=T ； x y tan =的对称中心为点0,πk 和点0,2ππ+k ； )tan(ϕω+=x A y 的周期ωπ=T ；4、函数)0,0)(sin(>>+=ωϕωA x A y 的相关概念：)sin(ϕω+=x A y 的图象与x y sin =的关系：①、振幅变换：x y sin = x A y sin =②、周期变换：x y sin = x y ωsin =③、相位变换：x y sin = )sin(ϕ+=x y④、平移变换：x A y ωsin = )sin(ϕω+=x A y 常叙述成： ①、把x y sin =上的所有点向左0>ϕ时或向右0<ϕ时平移|ϕ|个单位得到)sin(ϕ+=x y ； ②、再把)sin(ϕ+=x y 的所有点的横坐标缩短1>ω或伸长<01<ω到原来的ω1倍纵坐标不变得到)sin(ϕω+=x y ；③、再把)sin(ϕω+=x y 的所有点的纵坐标伸长1>A 或缩短<01<A 到原来的A 倍横坐标不变得到)sin(ϕω+=x A y 的图象; 先平移后伸缩的叙述方向：)sin(ϕω+=x A y先平移后伸缩的叙述方向： )](sin[)sin(ωϕωϕω+=+=x A x A y 10、三角函数求值域当A 1>时,图象上各点的纵坐标伸长到原来的A 倍当<0A 1<时,图象上各点的纵坐标缩短到原来的A 倍 当1>ω时,图象上各点的纵坐标缩短到原来的ω1倍当<01<ω时,图象上各点的纵坐标伸长到原来的ω1倍当0>ϕ时,图象上的各点向左平移ϕ个单位倍当0<ϕ时,图象上的各点向右平移||ϕ个单位倍当0>ϕ时,图象上的各点向左平移ωϕ个单位倍 当0<ϕ时,图象上的各点向右平移||ωϕ个单位倍1一次函数型：B x A y +=sin ,例：5)123sin(2+--=πx y ,x x y cos sin =用辅助角公式化为：=+=x b x a y cos sin )sin(22ϕ+⋅+x b a ,例：x x y cos 3sin 4-=2二次函数型：①、二倍角公式的应用：x x y 2cos sin += ②、代数代换：x x x x y cos sin cos sin ++=第五章、平面向量1、空间向量：1、定义：既有大小又有方向的量叫做向量,向量都可用同一平面内的有向线段表示;2、零向量：长度为0的向量叫零向量,记作0；零向量的方向是任意的;3、单位向量：长度等于1个单位长度的向量叫单位向量；与向量a 平行的单位向量：||a a e =；4、平行向量：方向相同或相反的非零向量叫平行向量也叫共线向量,记作b a //；规定0与任何向量平行；5、相等向量：长度相同且方向相同的向量叫相等向量,零向量与零向量相等；任意两个相等的非零向量,都可以用同一条有向线段来表示,并且与有向线段的起点无关; 2、向量的运算：1、向量的加减法：2、实数与向量的积：①、定义：实数λ与向量a 的积是一个向量,记作：a λ； ②：它的长度：||||||a a ⋅=λλ；③：它的方向：当0>λ,a λ与向量a 的方向相同；当0<λ,a λ与向量a 的方向相反；当0=λ时,a λ=0； 3、平面向量基本定理：如果21,e e 是同一平面内的两个不共线的向量,那么对平面内的任一向量a ,有且只有一对实数21,λλ,使2211e e a λλ+=；不共线的向量21,e e 叫这个平面内所有向量的一组基向量,{21,e e }叫基底;4、平面向量的坐标运算：１、运算性质：()()a a a cb ac b a a b b a =+=+++=+++=+00,, ２、坐标运算：设()()2211,,,y x b y x a ==→→,则()2121,y y x x b a ±±=±→→设A 、B 两点的坐标分别为x 1,y 1,x 2,y 2,则()1212,y y x x AB --=→. 3、实数与向量的积的运算律: 设()y x a ,=→,则λ()()y x y x a λλλ,,==→,4、平面向量的数量积：①、 定义：⎪⎭⎫ ⎝⎛≤≤≠≠⋅=⋅→→→→→→→→001800,0,0cos θθb a b a b a , 00=⋅→→a . ①、平面向量的数量积的几何意义：向量a 的长度|a |与b 在a 的方向上的投影|b |θcos 的乘积； ③、坐标运算:设()()2211,,,y x b y x a ==→→,则2121y y x x b a +=⋅→→ ；向量a 的模|a |：a a a ⋅=2||22y x +=；模|a |22y x +=④、设θ是向量()()2211,,,y x b y x a ==→→的夹角,则222221212121cos y x y x y y x x +++=θ,a ⊥b 0=⋅⇔b a5、重要结论：1、两个向量平行的充要条件： →→→→=⇔b a b a λ// )(R ∈λ设()()2211,,,y x b y x a ==→→,则⇔→→b a // 01221=-y x y x 2、两个非零向量垂直的充要条件：0=⋅⇔⊥→→→→b a b a设 ()()2211,,,y x b y x a ==→→,则 02121=+⇔⊥→→y y x x b a 3、两点()()2211,,,y x B y x A 的距离：221221)()(||y y x x AB -+-=4、P 分线段P 1P 2的：设Px,y ,P 1x 1,y 1 ,P 2x 2,y 2 ,且→→=21PP P P λ ,即||21PP P P =λ则定比分点坐标公式⎪⎪⎩⎪⎪⎨⎧++=++=λλλλ112121y y y x x x , 中点坐标公式⎪⎪⎩⎪⎪⎨⎧+=+=222121y y y x x x 5、平移公式：如果点 Px,y 按向量()k h a ,=→平移至P ′x ′,y ′,则⎪⎩⎪⎨⎧+=+=.,''k y y h x x。

中考生常用三角函数公式1、同角三角函数的差不多关系倒数关系: tan cot＝1 sin csc＝1 cos sec＝1商的关系：sin/cos＝tan＝sec/csc cos/sin＝cot＝csc/sec平方关系：sin^2()＋cos^2()＝1 1＋tan^2()＝sec^2() 1＋cot^2()＝csc^2()平常针对不同条件的常用的两个公式sin +cos =1tan *cot =1一个专门公式（sina+sin）*（sina+sin）=sin（a+）*sin（a-）2、锐角三角函数公式正弦：sin =的对边/ 的斜边余弦：cos =的邻边/的斜边正切：tan =的对边/的邻边余切：cot =的邻边/的对边3、二倍角公式正弦sin2A=2sinAcosA余弦1.Cos2a=Cos^2(a)-Sin^2(a) =2Cos^2(a)-1 =1-2Sin^2(a)2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1正切tan2A=（2tanA）/（1-tan^2(A)）4、三倍角公式sin3=4sinsin(/3+)sin(/3-)cos3=4coscos(/3+)cos(/3-)tan3a = tan a tan(/3+a) tan(/3-a)5、n倍角公式sin（n a）=Rsina sin（a+/n）……sin（a+（n-1）/n）。

其中R=2^（n-1）6、半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA); cot(A/2)=sinA/(1-cosA)=(1+cos A)/sinA. sin^2(a/2)=(1-cos(a))/2 cos^2(a/2)=(1+cos(a))/2 tan(a/2)=(1-cos(a))/s in(a)=sin(a)/(1+cos(a))7、和差化积sin+sin = 2 sin[(+)/2] cos[(-)/2]sin-sin = 2 cos[(+)/2] sin[(-)/2]cos+cos = 2 cos[(+)/2] cos[(-)/2]cos-cos = -2 sin[(+)/2] sin[(-)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)8、两角和公式cos(+)=coscos-sinsincos(-)=coscos+sinsinsin(+)=sincos+cossinsin(-)=sincos -cossin9、积化和差sinsin = [cos(-)-cos(+)] /2 coscos = [cos(+)+cos(-)]/2 sincos = [sin(+) +sin(-)]/2 cossin = [sin(+)-sin(-)]/210、双曲函数sinh(a) = [e^a-e^(-a)]/2 cosh(a) = [e^a+e^(-a)]/2 tanh(a) = sin h(a)/cos h(a)公式一：设为任意角，终边相同的角的同一三角函数的值相等：sin（2 k＋）= sin cos（2k＋）= cos tan（2k＋）= tan cot（2k＋）= cot 公式二：设为任意角，的三角函数值与的三角函数值之间的关系：sin （＋）= -sin cos（＋）= -cos tan（＋）= tan cot（＋）= cot 公式三：任意角与-的三角函数值之间的关系：sin（-）= -sin cos（-）= cos tan（-）= -tan cot（-）= -cot公式四：利用公式二和公式三能够得到与的三角函数值之间的关系：s in（）= sin cos（）= -cos tan（）= -tan cot（）= -cot公式五：利用公式-和公式三能够得到2与的三角函数值之间的关系：s in（2）= -sin cos（2）= cos tan（2）= -tan cot（2）= -cot公式六：/2及3/2与的三角函数值之间的关系：sin（/2+）= cos cos（/ 2+）= -sin tan（/2+）= -cot cot（/2+）= -tan sin（/2-）= cos cos（/2-）=sin tan（/2-）= cot cot（/2-）= tan sin（3/2+）= -cos cos（3/2+）= sin tan（3/2+）= -cot cot（3/2+）= -tan sin（3/2-）= -cos cos（3/2-）= -sin tan（3/2-）= cot cot（3/2-）= tan (以上kZ) Asin(t+)+ Bsin(t+) = {(A +B +2ABcos(-)} sin{ t + arcsin[ (Asin+Bsin) / {A^2 +B^2; +2ABcos(-)} } 表示根号,包括{……}中的内容11、诱导公式sin(-) = -sin cos(-) = cos tan (-)=-tan sin(/2-) = cos cos(/2-) = sin si n(/2+) = cos cos(/2+) = -sin sin() = sin cos() = -cos sin() = -sin cos() = -cos tanA= sinA/cosA tan（/2＋）＝－cot tan（/2－）＝cot tan（－）＝－tan tan（＋）＝tan 诱导公式记背诀窍：奇变偶不变，符号12、万能公式sin=2tan(/2)/[1+(tan(/2))] cos=[1-(tan(/2))]/[1+(tan(/2))] tan=2tan(/2)/[1-(t an(/2))]13、其它公式(1) (sin)+(cos)=1(2)1+(tan)=(sec)(3)1+(cot)=(csc)(4)关于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC (5)cotA cotB+cotAcotC+cotBcotC=1 (6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)c ot(C/2)(7)(cosA）+(cosB）+(cosC）=1-2cosAcosBcosC(8)（sinA）+（sinB）+（sinC）=2+2cosAcosBcosC家庭是幼儿语言活动的重要环境，为了与家长配合做好幼儿阅读训练工作，小孩一入园就召开家长会，给家长提出早期抓好幼儿阅读的要求。