初中数学三角函数公式汇总,没有比这更全的!

初中数学必背三角函数公式大全三角函数是初中数学中非常重要的概念之一，它在解决各种与三角形相关的问题时起着关键作用。

在学好三角函数的过程中，熟练掌握一些重要的三角函数公式是必不可少的。

本文将介绍初中数学必背的三角函数公式，帮助学生更好地理解和运用。

一、正弦函数公式正弦函数常用的公式有：1. 正弦定理：对于任意三角形ABC，有以下关系成立：a/sinA = b/sinB = c/sinC = 2R其中，a、b、c分别表示三角形ABC的三边长度，A、B、C表示其对应的角，R表示三角形的外接圆半径。

2. 余弦定理：对于任意三角形ABC，有以下关系成立：a^2 = b^2 + c^2 - 2bc·cosAb^2 = a^2 + c^2 - 2ac·cosBc^2 = a^2 + b^2 - 2ab·cosC其中，a、b、c分别表示三角形ABC的三边长度，A、B、C表示其对应的角。

3. 正弦函数的基本关系：对于任意角θ，其正弦函数的定义为：s inθ = y/r其中，y表示角θ所对应的直角三角形的对边长度，r表示斜边长度。

二、余弦函数公式余弦函数常用的公式有：1. 余弦函数的基本关系：对于任意角θ，其余弦函数的定义为：cosθ = x/r其中，x表示角θ所对应的直角三角形的邻边长度，r表示斜边长度。

2. 正弦与余弦的关系：对于任意角θ，有以下关系成立：sin^2θ + cos^2θ = 1三、正切函数公式正切函数常用的公式有：1. 正切函数的基本关系：对于任意角θ，其正切函数的定义为：tanθ = y/x其中，y表示角θ所对应的直角三角形的对边长度，x表示邻边长度。

2. 正切函数的倒数关系：对于任意角θ，有以下关系成立：tanθ = 1/cotθ其中，cotθ表示θ的余切值。

四、其他重要公式除了前面介绍的三角函数公式外，还有一些其他重要的公式，如：1. 三角函数的正负关系：对于任意角θ，有以下关系成立：sin(-θ) = -sinθcos(-θ) = cosθ2. 倍角公式：对于任意角θ，有以下关系成立：sin(2θ) = 2sinθ·cosθcos(2θ) = cos^2θ - sin^2θ = 1 - 2sin^2θ = 2cos^2θ - 13. 半角公式：对于任意角θ/2，有以下关系成立：sin(θ/2) = ±√[(1 - cosθ)/2]cos(θ/2) = ±√[(1 + cosθ)/2]其中，正负号由θ的象限决定。

初中数学三角函数公式汇总一、正弦函数公式1. 正弦函数的基本定义：在直角三角形中，对于一个锐角A，正弦函数定义为：sin A = 对边 / 斜边2. 正弦函数的倒数公式：两个锐角的正弦函数互为倒数，即：sin (90° - A) = 1 / sin A3. 正弦函数的和差公式：sin (A ± B) = sin A · cos B ± cos A · sin B4. 正弦函数的倍角公式：sin 2A = 2 · sin A · cos A二、余弦函数公式1. 余弦函数的基本定义：在直角三角形中，对于一个锐角A，余弦函数定义为：cos A = 邻边 / 斜边2. 余弦函数的倒数公式：两个锐角的余弦函数互为倒数，即：cos (90° - A) = 1 / cos A3. 余弦函数的和差公式：cos (A ± B) = cos A · cos B ∓ sin A · sin B4. 余弦函数的倍角公式：cos 2A = cos²A - sin²A = 2 · cos²A - 1 = 1 - 2 · sin²A三、正切函数公式1. 正切函数的基本定义：在直角三角形中，对于一个锐角A，正切函数定义为：tan A = 对边 / 邻边2. 正切函数的倒数公式：两个锐角的正切函数互为倒数，即：tan (90° - A) = 1 / tan A3. 正切函数的和差公式：tan (A ± B) = (tan A ± tan B) / (1 ∓ tan A · tan B)4. 正切函数的倍角公式：tan 2A = (2 · tan A) / (1 - tan²A)四、余切函数公式1. 余切函数的基本定义：在直角三角形中，对于一个锐角A，余切函数定义为：cot A = 邻边 / 对边 = 1 / tan A2. 余切函数的倒数公式：两个锐角的余切函数互为倒数，即：cot (90° - A) = 1 / cot A3. 余切函数的和差公式：cot (A ± B) = (cot A · cot B - 1) / (cot B ± cot A)4. 余切函数的倍角公式：cot 2A = (cot²A - 1) / (2 · cot A)五、正割函数和余割函数公式1. 正割函数的定义：在直角三角形中，对于一个锐角A，正割函数定义为：sec A = 斜边 / 邻边 = 1 / cos A2. 余割函数的定义：在直角三角形中，对于一个锐角A，余割函数定义为：csc A = 斜边 / 对边 = 1 / sin A以上是初中数学常见的三角函数公式汇总，这些公式在解决三角函数相关问题时非常有用。

三角函数公式大全三角函数是数学中非常重要的一个分支，广泛应用于物理学、工程学、计算机科学等多个领域。

下面为大家带来一份三角函数公式大全。

一、基本三角函数1、正弦函数（sin）：在直角三角形中，一个锐角的正弦是它的对边与斜边的比值。

即 sinA ＝ a ／ c （其中 A 为锐角，a 为 A 的对边，c 为斜边）。

2、余弦函数（cos）：一个锐角的余弦是它的邻边与斜边的比值。

即 cosA ＝ b ／ c （其中 b 为 A 的邻边）。

3、正切函数（tan）：一个锐角的正切是它的对边与邻边的比值。

即 tanA ＝ a ／ b 。

二、同角三角函数基本关系1、平方关系：sin²A ＋ cos²A ＝ 1 。

2、商数关系：tanA ＝ sinA ／ cosA 。

三、诱导公式1、终边相同的角的三角函数值相等：sin(2kπ ＋ A) ＝ sinA ，cos(2kπ ＋ A) ＝ cosA ，tan(2kπ ＋ A) ＝ tanA （k ∈ Z）。

2、关于 x 轴对称：sin(A) ＝ sinA ，cos(A) ＝ cosA ，tan(A) ＝tanA 。

3、关于 y 轴对称：sin(π A) ＝ sinA ，cos(π A) ＝ cosA ，tan(π A) ＝ tanA 。

4、关于原点对称：sin(π ＋ A) ＝ sinA ，cos(π ＋ A) ＝ cosA ，tan(π ＋ A) ＝ tanA 。

5、 90°相关：sin(π/2 A) ＝ cosA ，cos(π/2 A) ＝ sinA 。

四、两角和与差的三角函数公式1、两角和的正弦：sin(A ＋ B) ＝ sinAcosB ＋ cosAsinB 。

2、两角差的正弦：sin(A B) ＝ sinAcosB cosAsinB 。

3、两角和的余弦：cos(A ＋ B) ＝ cosAcosB sinAsinB 。

4、两角差的余弦：cos(A B) ＝ cosAcosB ＋ sinAsinB 。

初中数学三角函数公式最全三角函数是数学中重要的概念和工具之一，在初中数学中也是一个重要的知识点。

掌握了三角函数的基本概念和公式，可以解决很多几何和物理相关的问题。

下面将介绍一些初中数学中三角函数的常见公式。

1.正弦定理：在任意三角形ABC中，边长分别为a，b，c，对应的角度为A，B，C。

则有：a/sin A = b/sin B = c/sin C2.余弦定理：在任意三角形ABC中，边长分别为a，b，c，对应的角度为A，B，C。

则有：c^2 = a^2 + b^2 - 2ab cos C3.正弦函数的性质：sin(A ± B) = sin A cos B ± cos A sin Bsin(180° ± θ) = ±sin θsin²θ + cos²θ = 1sin²θ = 1/2(1 - cos 2θ)4.余弦函数的性质：cos(A ± B) = cos A cos B ∓ sin A sin Bcos(180° ± θ) = -cos θcos²θ + sin²θ = 1cos²θ = 1/2(1 + cos 2θ)5.正切函数的性质：tan(A ± B) = (tan A ± tan B) / (1 ∓ tan A tan B) tan(180° ± θ) = ±tan θ6.三角函数的周期性：sin(θ ± 360°n) = sin θcos(θ ± 360°n) = cos θtan(θ ± πn) = tan θ7.三角函数的倒数关系：sin θ = 1 / csc θcos θ = 1 / sec θtan θ = 1 / cot θ8.三角函数的和差化积公式：sin(A ± B) = sin A cos B ± cos A sin Bcos(A ± B) = cos A cos B ∓ sin A sin Btan(A ± B) = (tan A ± tan B) / (1 ∓ tan A tan B)9.三角函数的倍角公式：sin 2θ = 2sin θ cos θcos 2θ = cos²θ - sin²θ= 2cos²θ - 1= 1 - 2sin²θtan 2θ = 2tan θ / (1 - tan²θ)10.三角函数的半角公式：sin(θ/2) = ±√[(1 - cos θ)/2]cos(θ/2) = ±√[(1 + cos θ)/2]tan(θ/2) = ±√[(1 - cos θ)/(1 + cos θ)]以上是初中数学中常见的三角函数公式，可以通过这些公式来解决各种三角函数的计算问题。

三角函数公式大全及记忆口诀一、正弦函数（sine function）公式：1. 正弦函数的定义：在直角三角形中，正弦函数是对边与斜边之比，表示为sinθ。

2. 正弦函数的基本关系式：sinθ = 对边 / 斜边3. 弦函数的平方和恒等式：sin²θ + cos²θ = 1二、余弦函数（cosine function）公式：1. 余弦函数的定义：在直角三角形中，余弦函数是邻边与斜边之比，表示为cosθ。

2. 余弦函数的基本关系式：cosθ = 邻边 / 斜边3. 弦函数与余弦函数的关系：cosθ = sin(90° - θ)三、正切函数（tangent function）公式：1. 正切函数的定义：在直角三角形中，正切函数是对边与邻边之比，表示为tanθ。

2. 正切函数的基本关系式：tanθ = 对边 / 邻边3. 弦函数与正切函数的关系：tanθ = sinθ / cosθ四、余切函数（cotangent function）公式：1. 余切函数的定义：在直角三角形中，余切函数是邻边与对边之比，表示为cotθ。

2. 余切函数的基本关系式：cotθ = 邻边 / 对边3. 弦函数与余切函数的关系：cotθ = 1 / tanθ = cosθ / sinθ五、正割函数（secant function）公式：1. 正割函数的定义：在直角三角形中，正割函数是斜边与邻边之比，表示为secθ。

2. 正割函数的基本关系式：secθ = 斜边 / 邻边= 1 / cosθ六、余割函数（cosecant function）公式：1. 余割函数的定义：在直角三角形中，余割函数是斜边与对边之比，表示为cscθ。

2. 余割函数的基本关系式：cscθ = 斜边 / 对边= 1 / sinθ七、和差公式：1. 正弦函数和差公式：sin(θ±φ) = sinθcosφ ± cosθsinφ2. 余弦函数和差公式：cos(θ±φ) = cosθcosφ ∓ sinθsinφ3. 正切函数和差公式：tan(θ±φ) = (tanθ ± tanφ) / (1 ∓tanθtanφ)八、倍角公式：1. 正弦函数倍角公式：sin2θ = 2sinθcosθ2. 余弦函数倍角公式：cos2θ = cos²θ - sin²θ = 2cos²θ - 1= 1 - 2sin²θ3. 正切函数倍角公式：tan2θ = (2tanθ) / (1 - tan²θ)九、半角公式：1. 正弦函数半角公式：sin(θ/2) = ±√[(1 - cosθ) / 2]2. 余弦函数半角公式：cos(θ/2) = ±√[(1 + cosθ) / 2]3. 正切函数半角公式：tan(θ/2) = ±√[(1 - cosθ) / (1 +cosθ)]十、和差化积公式：1. 正弦函数和差化积公式：sinθ ± sinφ = 2sin[(θ ±φ)/2]cos[(θ ∓ φ)/2]2. 余弦函数和差化积公式：cosθ + cosφ = 2cos[(θ +φ)/2]cos[(θ - φ)/2]3. 正切函数和差化积公式：tanθ ± tanφ = sin(θ ± φ) /cosθcosφ以上是三角函数的常用公式。

初中三角函数常用公式大全一、基本关系式：1. 正弦定理：在任意三角形ABC中，有a/sinA=b/sinB=c/sinC=2R，其中a，b，c分别为三角形ABC的三边，A，B，C为对应的角，R为三角形的外接圆半径。

2. 余弦定理：在任意三角形ABC中，有c²=a²+b²-2abcosC。

3. 正弦公式：在任意三角形ABC中，有sinA/a=sinB/b=sinC/c。

4. 余弦公式：在任意三角形ABC中，有cosA=(b²+c²-a²)/2bc，cosB=(c²+a²-b²)/2ac，cosC=(a²+b²-c²)/2ab。

二、常用比值关系：1. 任意角的正弦公式：在直角三角形中，sinθ=对边/斜边。

2. 任意角的余弦公式：在直角三角形中，cosθ=邻边/斜边。

3. 任意角的正切公式：在直角三角形中，tanθ=对边/邻边。

4. 任意角的余切公式：在直角三角形中，cotθ=邻边/对边。

5. 任意角的正割公式：在直角三角形中，secθ=斜边/邻边。

6. 任意角的余割公式：在直角三角形中，cscθ=斜边/对边。

三、特殊角的值：1. π/6的正弦和余弦值：sin(π/6)=1/2，cos(π/6)=√3/22. π/4的正弦和余弦值：sin(π/4)=cos(π/4)=√2/23. π/3的正弦和余弦值：sin(π/3)=√3/2，cos(π/3)=1/24. π/2的正弦和余弦值：sin(π/2)=1，cos(π/2)=0。

四、和差化积公式：1. sin(A±B)=sinAcosB±cosAsinB。

2. cos(A±B)=cosAcosB∓sinAsinB。

3. tan(A±B)=(tanA±tanB)/(1∓tanAtanB)。

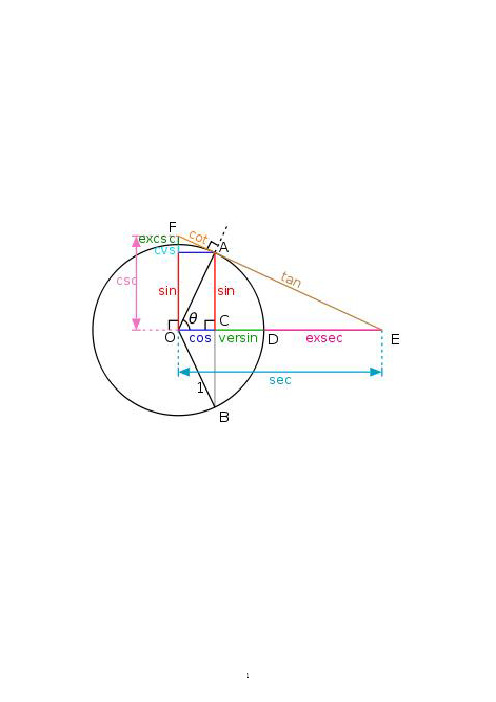
三角函数公式一、任意角的三角函数在角α的终边上任取．．一点),(y x P ,记：22y x r +=， 正弦函数：r y=αsin 余弦函数：r x =αcos 正切函数：x y =αtan余切函数：y x =αcot 正割函数：xr=αsec余割函数：yr=αcsc二、同角三角函数的基本关系式六边形记忆法：图形结构“上弦中切下割,左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。

”倒数关系：1csc sin =⋅x x ,1sec cos =⋅x x ，1cot tan =⋅x x 。

商数关系：x x x cos sin tan =，xxx sin cos cot =。

平方关系：1cos sin 22=+x x ，x x 22sec tan 1=+，x x 22csc cot 1=+。

积的关系：sinx=tanx·cosx cosx=sinx·cotx tanx=sinx·secxcotx=cosx·cscx secx=tanx·cscx cscx=secx·cotx三、诱导公式公式一：设α为任意角,终边相同的角的同一三角函数的值相等:sin（2kπ＋α）＝sinα cos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanα cot（2kπ＋α)＝cotα (其中k∈Z) 公式二：设α为任意角，π＋α的三角函数的值与α的三角函数值之间的关系： sin（π＋α）＝－sinα cos（π＋α）＝－cosα tan（π＋α）＝tanα cot（π＋α）＝cotα公式三：任意角α与－α的三角函数值之间的关系： sin（－α）＝－sinα cos（－α）＝cosα tan(－α）＝－tanα cot（－α）＝－cotα公式四：利用公式二和公式三可以得到π－α与α的三角函数值之间的关系： sin（π－α）＝sinα cos（π－α）＝－cosα tan（π－α）＝－tanα cot(π－α）＝－cotα 公式五：απ-2与α的三角函数值之间的关系:sin（απ-2）＝cosα cos（απ-2）＝sinα tan（απ-2）＝cotα cot（απ-2）＝tanα公式六:απ+2与α的三角函数值之间的关系:sin（απ+2）＝cosα cos（απ+2）＝－sinαtan(απ+2)＝－cotα cot（απ+2）＝－tanα公式七：απ-23与α的三角函数值之间的关系：sin(απ-23）＝－cosα cos（απ-23）＝－sinαtan（απ-23)＝cotα cot（απ-23）＝tanα公式八：απ+23与α的三角函数值之间的关系：sin(απ+23）＝－cosα cos（απ+23）＝sinαtan（απ+23）＝－cotα cot（απ+23）＝－tanα公式九：利用公式一和公式三可以得到2π－α与α的三角函数值之间的关系： sin（2π－α)＝－sinα cos(2π－α）＝cosα tan（2π－α)＝－tanα cot（2π－α）＝－cotα⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值，前面加上一个把α看成．．锐角时原函数值的符号。

三角函数公式大全三角函数是数学中一个重要的分支，在几何、物理、工程等众多领域都有着广泛的应用。

掌握三角函数的公式对于解决相关问题至关重要。

下面就为大家呈现一份较为全面的三角函数公式大全。

一、基本三角函数定义在直角三角形中，我们定义三个基本的三角函数：正弦（sin）、余弦（cos）和正切（tan）。

对于一个锐角θ，其对边与斜边的比值为正弦，即sinθ ＝对边／斜边；邻边与斜边的比值为余弦，即cosθ ＝邻边／斜边；对边与邻边的比值为正切，即tanθ ＝对边／邻边。

二、同角三角函数基本关系1、平方关系：sin²θ ＋cos²θ ＝ 1这意味着对于任何一个角度θ，其正弦的平方加上余弦的平方总是等于 1。

2、商数关系：tanθ ＝sinθ ／cosθ三、诱导公式诱导公式用于将任意角的三角函数值转化为锐角的三角函数值。

1、sin(α) ＝sinα，cos(α) ＝cosα，tan(α) ＝tanα2、sin(π ＋α) ＝sinα，cos(π ＋α) ＝cosα，tan(π ＋α) ＝tanα3、sin(π α) ＝ si nα，cos(π α) ＝cosα，tan(π α) ＝tanα4、sin(2π α) ＝sinα，cos(2π α) ＝cosα，tan(2π α) ＝tanα四、两角和与差的三角函数公式1、sin(α ＋β) ＝sinαcosβ ＋cosαsinβ2、sin(α β) ＝sinαcosβ cosαsinβ3、cos(α ＋β) ＝cosαcosβ sinαsinβ4、cos(α β) ＝cosαcosβ ＋sinαsinβ5、 tan(α ＋β) ＝（tanα ＋tanβ) ／（1 tanαtanβ)6、tan(α β) ＝（tanα tanβ) ／（1 ＋tanαtanβ)五、二倍角公式1、sin2α ＝2sinαcosα2、cos2α ＝cos²α sin²α ＝2cos²α 1 ＝1 2sin²α3、tan2α ＝2tanα ／（1 tan²α)六、半角公式1、sin²(α/2) ＝（1 cosα) ／ 22、cos²(α/2) ＝（1 ＋cosα) ／ 23、tan(α/2) ＝（1 cosα) ／sinα ＝sinα ／（1 ＋cosα)七、万能公式1、sinα ＝2tan(α/2) ／（1 ＋tan²(α/2)）2、cosα ＝（1 tan²(α/2)）／（1 ＋tan²(α/2)）3、tanα ＝2tan(α/2) ／（1 tan²(α/2)）八、积化和差公式1、sinαcosβ ＝（1/2)sin(α ＋β) ＋sin(α β)2、cosαsinβ ＝（1/2)sin(α ＋β) sin(α β)3、cosαcosβ ＝（1/2)cos(α ＋β) ＋cos(α β)4、sinαsinβ ＝（1/2)cos(α ＋β) cos(α β)九、和差化积公式1、sinα ＋sinβ ＝2sin(α ＋β) ／2cos(α β) ／ 22、sinα sinβ ＝2cos(α ＋β) ／2sin(α β) ／ 23、cosα ＋cosβ ＝2cos(α ＋β) ／2cos(α β) ／ 24、cosα cosβ ＝－2sin(α ＋β) ／2sin(α β) ／ 2十、辅助角公式asinx ＋ bcosx ＝√（a²＋ b²)sin(x ＋φ)，其中tanφ ＝ b ／ a这些三角函数公式在解决各种数学问题中都有着重要的作用。

初中三角函数公式及定理大全1、正弦定理：在三角形中，各边和它所对的角的正弦的比相等，即a/sinA=b/sinB=c/sinC=2R 。

（其中R为外接圆的半径），2、第一余弦定理：三角形中任意一边等于其他两边以及对应角余弦的交叉乘积的和，即a=c cosB + b cosC。

初中三角函数公式及定理大全1锐角三角函数定义:锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec)，余割(csc)都叫做角A的锐角三角函数。

正弦(sin)：对边比斜边，即sinA=a/c余弦(cos)：邻边比斜边，即cosA=b/c正切(tan)：对边比邻边，即tanA=a/b余切(cot)：邻边比对边，即cotA=b/a正割(sec)：斜边比邻边，即secA=c/b余割(csc)：斜边比对边，即cscA=c/a初中三角函数公式及定理大全2互余角的关系sin(π-α)=cosα, cos(π-α)=sinα,tan(π-α)=cotα, cot(π-α)=tanα.积的关系sinα=tanα·cosαcosα=cotα·sinαtanα=sinα·secαcotα=cosα·cscαsecα=tanα·cscαcscα=secα·cotα初中三角函数公式及定理大全3平方关系sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)倒数关系tanα·cotα=1sinα·cscα=1cosα·secα=1初中三角函数公式及定理大全4三角函数的和差化积公式sinA+sinB=2sin[(A+B)/2]cos[(A-B)/2]sinA-sinB=2cos[(A+B)/2]sin[(A-B)/2]cosA+cosB=2cos[(A+B)/2]cos[(A-B)/2]cosA-cosB=-2sin[(A+B)/2]sin[(A-B)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)。

初中三角函数公式大全一、正弦定理在任意三角形ABC中，我们可以利用正弦定理计算三角形的边与角之间的关系。

正弦定理的表达式如下：a/sinA = b/sinB = c/sinC其中a、b、c表示三角形的三条边的长度，A、B、C表示对应的内角。

利用正弦定理，我们可以求解出任意一个角的大小，或者求解出任意一条边的长度。

二、余弦定理余弦定理和正弦定理类似，也是用于计算三角形的边与角之间的关系。

余弦定理的表达式如下：c² = a² + b² - 2abcosCb² = a² + c² - 2accosBa² = b² + c² - 2bccosA其中a、b、c表示三角形的三条边的长度，A、B、C表示对应的内角。

余弦定理可以帮助我们计算三角形边的长度，特别是当已知两边和它们之间的夹角时。

三、正切公式对于任意角度θ，我们可以利用正切公式计算其正切值：tanθ = sinθ/cosθ正切公式可以帮助我们计算角度的正切值，常常用于解决与直角三角形相关的问题。

四、倍角公式倍角公式是用来计算角度的二倍角的三角函数值。

倍角公式的表达式如下：sin2θ = 2sinθcosθcos2θ = cos²θ - sin²θtan2θ = (2tanθ)/(1-tan²θ)五、半角公式半角公式是用来计算角度的一半或二分之一角的三角函数值。

半角公式的表达式如下：sin(θ/2) = ±√[(1-cosθ)/2]cos(θ/2) = ±√[(1+cosθ)/2]tan(θ/2) = ±√[(1-cosθ)/(1+cosθ)]半角公式可以帮助我们计算角度的一半或二分之一角的三角函数值。

六、常用的三角函数关系在学习三角函数时，我们需要掌握一些常用的三角函数关系。

这些关系可以帮助我们在不同的三角函数之间进行转换。

初中数学三角函数公式初中数学三角函数公式大全其它公式(1) (sinα)+(cosα)=1(2)1+(tanα)=(secα)(3)1+(cotα)=(cscα) 证明下面两式,只需将一式,左右同除(sinα)，第二个除(cosα)即可(4)对于任意非直角三角形,总有 tanA+tanB+tanC=tanAtanBtanC证: A+B=π-C tan(A+B)=tan(π-C) (tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得 tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)+(cosB)+(cosC)=1-2cosAcosBcosC(8)(sinA)+(sinB)+(sinC)=2+2cosAcosBcosC其他非重点三角函数csc(a) = 1/sin(a) sec(a) = 1/cos(a)上面的内容是初中数学三角函数公式大全之其它公式，想必同学们都能熟记于心了吧。

在即将到来的期末考试中，同学们想要拿高分就来关注我们的吧。

初中数学正方形定理公式关于正方形定理公式的内容精讲知识，希望同学们很好的掌握下面的内容。

正方形定理公式正方形的特征：①正方形的四边相等；②正方形的四个角都是直角；③正方形的两条对角线相等，且互相垂直平分，每一条对角线平分一组对角；正方形的判定：①有一个角是直角的菱形是正方形；②有一组邻边相等的矩形是正方形。

希望上面对正方形定理公式知识的讲解学习，同学们都能很好的掌握，相信同学们会取得很好的成绩的哦。

三角函数公式大全一、基本定义及性质1. 正弦函数（sin）：sin A = 对边 / 斜边cos A = 临边 / 斜边tan A = 对边 / 临边余切函数（cot）：cot A = 临边 / 对边2.零度三角函数：sin 0° = 0, cos 0° = 1, tan 0° = 0, cot 0° = ∞3.π/6弧度三角函数：sin (π/6) = 1/2, cos (π/6) = √3/2, tan (π/6) = 1/√3, cot (π/6) = √34.π/4弧度三角函数：sin (π/4) = √2/2, cos (π/4) = √2/2, tan (π/4) = 1, cot (π/4) = 15.π/3弧度三角函数：sin (π/3) = √3/2, cos (π/3) = 1/2, tan (π/3) = √3, cot (π/3) = 1/√36.相反角关系：sin (-A) = -sin A, cos (-A) = cos A, tan (-A) = -tan A, cot (-A) = -cot A7.90°三角函数：sin 90° = 1, cos 90° = 0, tan 90° = ∞, cot 90° = 08.π/2弧度三角函数：sin (π/2) = 1, cos (π/2) = 0, tan (π/2) = ∞, cot (π/2) = 09.倒数关系：sin (π - A) = sin A, cos (π - A) = -cos A, tan (π - A) = -tan A, cot (π - A) = -cot A10.余角关系：sin (π/2 - A) = cos A, cos (π/2 - A) = sin A, tan (π/2 -A) = cot A, cot (π/2 - A) = tan A二、和差与倍角公式1.和差公式：sin (A ± B) = sin A cos B ± cos A sin Bcos (A ± B) = cos A cos B ∓ sin A sin Btan (A ± B) = (tan A ± tan B) / (1 ∓ tan A tan B)2.二倍角公式：sin 2A = 2 sin A cos Acos 2A = cos^2 A - sin^2 A = 2 cos^2 A - 1 = 1 - 2 sin^2 A tan 2A = (2 tan A) / (1 - tan^2 A)三、万能角公式（三角函数的倒数、减角公式、二倍角公式的推广形式）1.正弦函数倒数公式：csc A = 1 / sin A2.余弦函数倒数公式：sec A = 1 / cos A3.正切函数倒数公式：cot A = 1 / tan A4.减角公式：sin (A - B) = sin A cos B - cos A sin Bcos (A - B) = cos A cos B + sin A sin Btan (A - B) = (tan A - tan B) / (1 + tan A tan B)5.二倍角公式推广形式：sin 2A = 2 sin A cos Acos 2A = cos^2 A - sin^2 A = 2 cos^2 A - 1 = 1 - 2 sin^2 A tan 2A = (2 tan A) / (1 - tan^2 A)四、积和差公式1.积公式：sin A sin B = (1/2)[cos(A-B) - cos(A+B)]cos A cos B = (1/2)[cos(A-B) + cos(A+B)]sin A cos B = (1/2)[sin(A-B) + sin(A+B)]2.差公式：sin A - sin B = 2 cos[(A+B)/2] sin[(A-B)/2]cos A - cos B = -2 sin[(A+B)/2] sin[(A-B)/2]sin A + sin B = 2 sin[(A+B)/2] cos[(A-B)/2]cos A + cos B = 2 cos[(A+B)/2] cos[(A-B)/2]五、其他重要性质1. 正弦函数的周期：2π，即sin (x + 2π) = sin x余弦函数的周期：2π，即cos (x + 2π) = cos x2.正弦函数的奇偶性：sin (-x) = -sin x，即 sin 函数是奇函数sin (π + x) = -sin x，即 sin 函数是周期为2π的周期函数3.余弦函数的奇偶性：cos (-x) = cos x，即 cos 函数是偶函数cos (π + x) = -cos x，即 cos 函数是周期为2π的周期函数4.正弦函数和余弦函数的间接关系：sin^2 x + cos^2 x = 1。

初中三角函数的公式有半角公式sin(A/2)=±√((1-cosA)/2)、倍角公式Sin2A=2SinA*CosA、两角和与差公式Sin2A=2SinA*CosA、平方关系公式sin²α+cos²α=1、倒数关系公式tanα·cotα=1等等。

1初中数学三角函数公式锐角三角函数公式sinα=∠α的对边/斜边cosα=∠α的邻边/斜边tanα=∠α的对边/∠α的邻边cotα=∠α的邻边/∠α的对边2倍角公式Sin2A=2SinA?CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1tan2A=(2tanA)/(1-tanA^2)(注：SinA^2是sinA的平方sin2(A))2初中三角函数正切定理公式在平面三角形中，正切定理说明任意两条边的和除第一条边减第二条边的差所得的商等于这两条边的对角的和的一半的正切除第一条边对角减第二条边对角的差的一半的正切所得的商。

正切定理：(a+b)/(a-b)=tan((α+β)/2)/tan((α-β)/2)。

3初中三角函数余弦定理定义：对于任意三角形，任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。

对于边长为a、b、c而相应角为A、B、C的三角形，有：a^2=b^2+c^2-2bc·cosAb^2=a^2+c^2-2ac·cosBc^2=a^2+b^2-2ab·cosC也可表示为：cosC=(a^2+b^2-c^2)/2abcosB=(a^2+c^2-b^2)/2accosA=(c^2+b^2-a^2)/2bc这个定理也可以通过把三角形分为两个直角三角形来证明。

如果这个角不是两条边的夹角，那么三角形可能不是唯一的(边-边-角)。

要小心余弦定理的这种歧义情况。

延伸定理：第一余弦定理(任意三角形射影定理)设△ABC的三边是a、b、c，它们所对的角分别是A、B、C，则有：a=b·cosC+c·cosB，b=c·cosA+a·cosC，c=a·cosB+b·cosA。

三角函数公式大全锐角三角函数公式sin α=∠α的对边/ 斜边cos α=∠α的邻边/ 斜边tan α=∠α的对边/ ∠α的邻边cot α=∠α的邻边/ ∠α的对边倍角公式Sin2A=2SinA CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1tan2A=2tanA/1-tanA^2注：SinA^2 是sinA的平方sin2A三倍角公式sin3α=4sinα·sinπ/3+αsinπ/3-αcos3α=4cosα·cosπ/3+αcosπ/3-αtan3a = tan a ·tanπ/3+a·tanπ/3-a三倍角公式推导sin3a=sin2a+a=sin2acosa+cos2asina辅助角公式Asinα+Bcosα=A^2+B^2^1/2sinα+t,其中sint=B/A^2+B^2^1/2cost=A/A^2+B^2^1/2tant=B/AAsinα+Bcosα=A^2+B^2^1/2cosα-t,tant=A/B降幂公式sin^2α=1-cos2α/2=versin2α/2cos^2α=1+cos2α/2=covers2α/2tan^2α=1-cos2α/1+cos2α推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=sinα/2+cosα/2^2=2sina1-sin²a+1-2sin²asina=3sina-4sin³acos3a=cos2a+a=cos2acosa-sin2asina=2cos²a-1cosa-21-sin²acosa=4cos³a-3cosasin3a=3sina-4sin³a=4sina3/4-sin²a=4sina√3/2²-sin²a=4sinasin²60°-sin²a=4sinasin60°+sinasin60°-sina=4sina2sin60+a/2cos60°-a/22sin60°-a/2cos60°-a/2=4sinasin60°+asin60°-acos3a=4cos³a-3cosa=4cosacos²a-3/4=4cosacos²a-√3/2²=4cosacos²a-cos²30°=4cosacosa+cos30°cosa-cos30°=4cosa2cosa+30°/2cosa-30°/2{-2sina+30°/2sina-30°/2}=-4cosasina+30°sina-30°=-4cosasin90°-60°-asin-90°+60°+a=-4cosacos60°-a-cos60°+a=4cosacos60°-acos60°+a上述两式相比可得tan3a=tanatan60°-atan60°+a半角公式tanA/2=1-cosA/sinA=sinA/1+cosA;cotA/2=sinA/1-cosA=1+cosA/sinA.sin^2a/2=1-cosa/2cos^2a/2=1+cosa/2tana/2=1-cosa/sina=sina/1+cosa三角和sinα+β+γ=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sin β·sinγcosα+β+γ=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sin β·cosγtanα+β+γ=tanα+tanβ+tanγ-tanα·tanβ·tanγ/1-tanα·tanβ-tanβ·tanγ-tan γ·tanα两角和差cosα+β=cosα·cosβ-sinα·sinβcosα-β=cosα·cosβ+sinα·sinβsinα±β=sinα·cosβ±cosα·sinβtanα+β=tanα+tanβ/1-tanα·tanβtanα-β=tanα-tanβ/1+tanα·tanβ和差化积sinθ+sinφ= 2 sinθ+φ/2 cosθ-φ/2sinθ-sinφ= 2 cosθ+φ/2 sinθ-φ/2cosθ+cosφ= 2 cosθ+φ/2 cosθ-φ/2cosθ-cosφ= -2 sinθ+φ/2 sinθ-φ/2tanA+tanB=sinA+B/cosAcosB=tanA+B1-tanAtanBtanA-tanB=sinA-B/cosAcosB=tanA-B1+tanAtanB积化和差sinαsinβ= cosα-β-cosα+β/2cosαcosβ= cosα+β+cosα-β/2sinαcosβ= sinα+β+sinα-β/2cosαsinβ= sinα+β-sinα-β/2诱导公式sin-α= -sinαcos-α= cosαtan —a=-tanαsinπ/2-α= cosαcosπ/2-α= sinαsinπ/2+α= cosαcosπ/2+α= -sinαsinπ-α= sinαcosπ-α= -cosαsinπ+α= -sinαcosπ+α= -cosαtanA= sinA/cosAtanπ/2＋α＝－cotαtanπ/2－α＝cotαtanπ－α＝－tanαtanπ＋α＝tanα诱导公式记背诀窍：奇变偶不变,符号看象限万能公式sinα=2tanα/2/1+tan＾α/2cosα=1-tan＾α/2/1+tan＾α/2tanα=2tanα/2/1-tan＾α/2其它公式1sinα^2+cosα^2=121+tanα^2=secα^231+cotα^2=cscα^2证明下面两式,只需将一式,左右同除sinα^2,第二个除cosα^2即可4对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-CtanA+B=tanπ-CtanA+tanB/1-tanAtanB=tanπ-tanC/1+tanπtanC整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπn∈Z时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论5cotAcotB+cotAcotC+cotBcotC=16cotA/2+cotB/2+cotC/2=cotA/2cotB/2cotC/27cosA^2+cosB^2+cosC^2=1-2cosAcosBcosC8sinA^2+sinB^2+sinC^2=2+2cosAcosBcosC9sinα+sinα+2π/n+sinα+2π2/n+sinα+2π3/n+……+sinα+2πn-1/n=0cosα+cosα+2π/n+cosα+2π2/n+cosα+2π3/n+……+cosα+2πn-1/n=0 以及sin^2α+sin^2α-2π/3+sin^2α+2π/3=3/2tanAtanBtanA+B+tanA+tanB-tanA+B=0。

初中关于三角函数的所有公式初中三角函数的公式有和差角公式、和差化积公式、积化和差公式、倍角公式、半角公式、万能公式等等，接下来看一下公式的具体内容。

三角函数的和差角公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-cossinBcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)三角函数的和差化积公式sinA+sinB=2sin[(A+B)/2]cos[(A-B)/2]sinA-sinB=2cos[(A+B)/2]sin[(A-B)/2]cosA+cosB=2cos[(A+B)/2]cos[(A-B)/2]cosA-cosB=-2sin[(A+B)/2]sin[(A-B)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)三角函数的积化和差公式sinAsinB=-[cos(A+B)-cos(A-B)]/2cosAcosB=[cos(A+B)+cos(A-B)]/2sinAcosB=[sin(A+B)+sin(A-B)]/2cosAsinB=[sin(A+B)-sin(A-B)]/2三角函数诱导公式诱导公式一：终边相同的角的同一三角函数的值相等设α为任意锐角，弧度制下的角的表示：sin(2kπ+α)=sinα(k∈Z)cos(2kπ+α)=cosα(k∈Z)tan(2kπ+α)=tanα(k∈Z)cot(2kπ+α)=cotα(k∈Z)诱导公式二：π+α的三角函数值与α的三角函数值之间的关系设α为任意角，弧度制下的角的表示：sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα诱导公式三：任意角α与-α的三角函数值之间的关系sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα诱导公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα诱导公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα诱导公式六：π/2±α及3π/2±α与α的三角函数值之间的关系sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanα三角函数的倍角公式Sin2A=2SinA*CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1 tan2A=(2tanA)/(1-tanA^2)三角函数的万能公式sin(a)=[2tan(a/2)]/[1+tan2(a/2)]cos(a)=[1-tan2(a/2)]/[1+tan2(a/2)]tan(a)=[2tan(a/2)]/[1-tan2(a/2)]。

中考生常用三角函数公式1、同角三角函数的差不多关系倒数关系: tan cot＝1 sin csc＝1 cos sec＝1商的关系：sin/cos＝tan＝sec/csc cos/sin＝cot＝csc/sec平方关系：sin^2()＋cos^2()＝1 1＋tan^2()＝sec^2() 1＋cot^2()＝csc^2()平常针对不同条件的常用的两个公式sin +cos =1tan *cot =1一个专门公式（sina+sin）*（sina+sin）=sin（a+）*sin（a-）2、锐角三角函数公式正弦：sin =的对边/ 的斜边余弦：cos =的邻边/的斜边正切：tan =的对边/的邻边余切：cot =的邻边/的对边3、二倍角公式正弦sin2A=2sinAcosA余弦1.Cos2a=Cos^2(a)-Sin^2(a) =2Cos^2(a)-1 =1-2Sin^2(a)2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1正切tan2A=（2tanA）/（1-tan^2(A)）4、三倍角公式sin3=4sinsin(/3+)sin(/3-)cos3=4coscos(/3+)cos(/3-)tan3a = tan a tan(/3+a) tan(/3-a)5、n倍角公式sin（n a）=Rsina sin（a+/n）……sin（a+（n-1）/n）。

其中R=2^（n-1）6、半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA); cot(A/2)=sinA/(1-cosA)=(1+cos A)/sinA. sin^2(a/2)=(1-cos(a))/2 cos^2(a/2)=(1+cos(a))/2 tan(a/2)=(1-cos(a))/s in(a)=sin(a)/(1+cos(a))7、和差化积sin+sin = 2 sin[(+)/2] cos[(-)/2]sin-sin = 2 cos[(+)/2] sin[(-)/2]cos+cos = 2 cos[(+)/2] cos[(-)/2]cos-cos = -2 sin[(+)/2] sin[(-)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)8、两角和公式cos(+)=coscos-sinsincos(-)=coscos+sinsinsin(+)=sincos+cossinsin(-)=sincos -cossin9、积化和差sinsin = [cos(-)-cos(+)] /2 coscos = [cos(+)+cos(-)]/2 sincos = [sin(+) +sin(-)]/2 cossin = [sin(+)-sin(-)]/210、双曲函数sinh(a) = [e^a-e^(-a)]/2 cosh(a) = [e^a+e^(-a)]/2 tanh(a) = sin h(a)/cos h(a)公式一：设为任意角，终边相同的角的同一三角函数的值相等：sin（2 k＋）= sin cos（2k＋）= cos tan（2k＋）= tan cot（2k＋）= cot 公式二：设为任意角，的三角函数值与的三角函数值之间的关系：sin （＋）= -sin cos（＋）= -cos tan（＋）= tan cot（＋）= cot 公式三：任意角与-的三角函数值之间的关系：sin（-）= -sin cos（-）= cos tan（-）= -tan cot（-）= -cot公式四：利用公式二和公式三能够得到与的三角函数值之间的关系：s in（）= sin cos（）= -cos tan（）= -tan cot（）= -cot公式五：利用公式-和公式三能够得到2与的三角函数值之间的关系：s in（2）= -sin cos（2）= cos tan（2）= -tan cot（2）= -cot公式六：/2及3/2与的三角函数值之间的关系：sin（/2+）= cos cos（/ 2+）= -sin tan（/2+）= -cot cot（/2+）= -tan sin（/2-）= cos cos（/2-）=sin tan（/2-）= cot cot（/2-）= tan sin（3/2+）= -cos cos（3/2+）= sin tan（3/2+）= -cot cot（3/2+）= -tan sin（3/2-）= -cos cos（3/2-）= -sin tan（3/2-）= cot cot（3/2-）= tan (以上kZ) Asin(t+)+ Bsin(t+) = {(A +B +2ABcos(-)} sin{ t + arcsin[ (Asin+Bsin) / {A^2 +B^2; +2ABcos(-)} } 表示根号,包括{……}中的内容11、诱导公式sin(-) = -sin cos(-) = cos tan (-)=-tan sin(/2-) = cos cos(/2-) = sin si n(/2+) = cos cos(/2+) = -sin sin() = sin cos() = -cos sin() = -sin cos() = -cos tanA= sinA/cosA tan（/2＋）＝－cot tan（/2－）＝cot tan（－）＝－tan tan（＋）＝tan 诱导公式记背诀窍：奇变偶不变，符号12、万能公式sin=2tan(/2)/[1+(tan(/2))] cos=[1-(tan(/2))]/[1+(tan(/2))] tan=2tan(/2)/[1-(t an(/2))]13、其它公式(1) (sin)+(cos)=1(2)1+(tan)=(sec)(3)1+(cot)=(csc)(4)关于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC (5)cotA cotB+cotAcotC+cotBcotC=1 (6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)c ot(C/2)(7)(cosA）+(cosB）+(cosC）=1-2cosAcosBcosC(8)（sinA）+（sinB）+（sinC）=2+2cosAcosBcosC家庭是幼儿语言活动的重要环境，为了与家长配合做好幼儿阅读训练工作，小孩一入园就召开家长会，给家长提出早期抓好幼儿阅读的要求。