第2课时 函数的解析式与定义域

科 目数学 年级 高三 备课人 高三数学组 第 课时 2.1函数的解析式及定义域与值域考纲定位 理解函数的概念；掌握简单函数的定义域的求法；掌握求解析式的常用方法.疑难提示 1、要注意区间的正确表示，特别是分清开区间与闭区间的区别；2、简单函数的定义域和值域的求法；3、对符号()y f x =的理解及解析式的求法.【考点整合】1、函数的概念设A 、B 是非空的数集，如果按照某种确定的对应关系f ，使对于集合A 中的 ，在集合B 中都有 的数()f x 和它对应，那么就称:f A B →为从集合A 到集合B 的一个函数，其中x 的取值范围A 叫函数的 ， 叫函数的值域，值域是 的子集.2、函数的三要素： 为函数的三要素.两函数相同，当且仅当3、函数的表示法有 ， 和 .4、映射的概念设A 、B 是两个非空的集合，如果按某一个确定的对应关系f ，使对于集合A 中的 ，在集合B 中都有 的元素y 和它对应，那么就称:f A B →为从集合A 到集合B 的一个映射.5、函数定义域的求法：6、基本初等函数的值域：(一次函数、二次函数、反比例函数、指数函数、对数函数、三角函数)【真题演练】1、(2011 浙江)设函数20()0x x f x x x -≤⎧=⎨>⎩若()4f a =，则实数a =（ ）A.-4或-2B.-4或2C.-2或4D.-2或22、(2012 江西)下列函数中，与函数31y x=定义域相同的函数是（ ） A.1sin y x = B.ln x y x = C.x y xe = D.sin x y x= 3、(2012 江西)设函数211()lg 1x x f x x x ⎧+≤=⎨>⎩若((10))f f =（ ） A.lg101 B.2 C.1 D.04、(2012 安徽)下列函数中，不满足(2)2()f x f x =的是（ ）A.()||f x x =B.()||f x x x =-C.()1f x x =+D.()f x x =-5、(2012 江苏)函数6()12log f x x =-的定义域为6、(2010 江苏)已知函数210()10x x f x x ⎧+≥=⎨<⎩，则满足不等式2(1)(2)f x f x ->的x 的取值范围是【经典例题】一、函数的定义域：例1、(1)函数(1)y x x x =-+的定义域为 ； (2)函数02lg(2)(1)12x y x x x -=+-+-的定义域为 ；(3)已知函数()y f x =的定义域是[0，4]，则2(1)(3)y f x f x x =++-的定义域是变式训练：1、若函数(1)y f x =+的定义域是[-2，3），则(21)y f x =-的定义域是2、若函数1()x f x e x m=-+的定义域是R ，则实数m 的取值范围是 二、函数的值域例2、分别求下列函数的值域(1)1y x =+ (2)22y x x =-+ (3)22([0,3])y x x x =-+∈ (4)213x y x +=- (5) (6)21y x x =+-变式训练：求下列函数的值域(1)246([1,5))y x x x =-+∈ (2)(0)cx d y a ax b+=≠+其中 (3)21y x x =-- (4)22225(12)1x x y x x x ++=≤≤++三、函数的解析式例3、(1)已知二次函数()f x 的最小值为4，且(2)(0)6f f ==，求()f x 的解析式(2)已知2(1)f x x x +=+,求()f x 的解析式；(3)已知2()()32f x f x x +-=+，求()f x 的解析式(4)已知函数2y x x =+与函数()y g x =的图象关于点(-2,3)对称，求()g x 的解析式(5)设()f x 是R 上的函数,且满足(0)1f =,并且对任意实数,x y 都有()()(21)f x y f x y x y -=--+，求()f x 的解析式变式训练：(1)已知2211()f x x x x +=+，求()f x ；(2)已知12()()3f x f x x+=，求()f x ；【作业】《胜券在握》P4页第1、2题；【上本作业】《胜券在握》P4页第3、4、5题.。

函数定义域与解析式【教学目标】一、函数定义域【知识点】1.函数是一种非空的数集组成的映射，是从自变量x 到应变量y 的对应关系；期中x 的范围叫做定义域；2.定义域的常见形式有分式，根式，指数，对数，复合函数以及抽象函数；【定义域常见类型】一 、具体函数定义域的常见类型：1.分式中分母不为零2.偶次根式非负3.零次幂底数非零4. 当题中出现多个函数的四则运算及复合时，注意考虑每一个函数定义域并取交集二 、抽象函数常见类型1.已知()f x 定义域求()()f g x 定义域2已知()()f g x 定义域求()f x 定义域3. 已知()()f g x 定义域求()()f h x 定义域（一）具体函数【例题讲解】★☆☆例题1：求函数11y x =+的定义域； 答案： {}|1x x ≠−解析： 10,1x x +≠≠−，{}|1x x ∴≠−★☆☆练习1．求函数2123y x x =−−的定义域； 答案：{}|13x x x ≠−≠且解析：2230x x −−≠()()310x x −+≠，{}|13x x x ∴≠−≠且★☆☆例题2． 求函数y答案：{}R|1x x ∈≥解析：,x x −≥≥101，{}R|1x x ∴∈≥★☆☆练习1：求函数y =答案：[)(,-],−∞⋃+∞13解析：2230x x −−≥，()()310x x −+≥13x x ≤−≥或，(][),,∴−∞−⋃+∞13 ★☆☆例题3．求函数()023y x =−的定义域 3,2⎫⎛⎫+∞⎪ ⎪⎭⎝⎭解析：230x −≠3,2⎫⎛⎫+∞⎪ ⎪⎭⎝⎭★☆☆练习1求函数0221x y x −⎛⎫= ⎪+⎝⎭的定义域 ()1,22,2⎫⎛⎫−+∞⎪ ⎪⎭⎝⎭()1,22,2⎫⎛⎫−+∞⎪ ⎪⎭⎝⎭★☆☆例题4．．求函数y解析：1010x x −≥−≥且★☆☆练习1．求函数()04y x =−的定义域； 答案：(][)(),13,44,+−∞−∞解析：2230x x −−≥且40x −≠(][)(),13,44,+x ∴∈−∞−∞（二）抽象函数★☆☆例题5．已知()f x 定义域是[]1,3，求()21f x +的定义域答案：[]0,1解析： 因为()f x 的定义是[]1,3,即()f x 中,[]1,3x ∈,那么()21f x +中,[]211,3x +∈,得[]0,1x ∈则()21f x +中,[]0,1x ∈∴ ()21f x +的定义域是[]0,1★☆☆练习1．已知()f x 定义域是()0,1，求()2f x 的定义域答案： ()()1,00,1−解析：因为()f x 的定义是()0,1,即()f x 中,()0,1x ∈,那么()2f x 中, ()20,1x ∈,得()()1,00,1x ∈−则()2f x 中, ()()1,00,1x ∈−∴ ()2f x 的定义域是()()1,00,1x ∈−★☆☆例题6．已知()1f x −定义域是[]3,3−，求()f x 的定义域.答案：[]4,2−．解析：∵()1f x −的定义域为[]3,3−，即33x −≤≤∴412x −≤−≤即函数()f x 定义域为[]4,2−．★☆☆练习1已知)2f 定义域是[]4,9，求()f x 的定义域答案：[]0,1即函数()f x 定义域为[]0,1．★☆☆例题7．已知()21f x +定义域是()3,5，求()41f x −的定义域答案：()2,3.解析：∵(21)f x +定义域为()3,5，即35x <<，∴72111x <+< ，则()f x 定义域为()7,11，∴(41)f x −定义域为74111x <−<，∴23x <<．即()41f x −的定义域为()2,3.★☆☆练习1已知()1f x +定义域是()2,3−，求()222f x −的定义域2,32⎫⎛⎪ ⎪ ⎭⎝解析：∵()1f x +定义域为()2,3−，即23x −<<，∴114x −<+< ，则()f x 定义域为()1,4−，∴()222f x −定义域为21224x −<−<， 2,32⎫⎛⎪ ⎪ ⎭⎝2,32⎫⎛⎪ ⎪ ⎭⎝★☆☆例题8．若函数()f x = 的定义域为R ，则实数a 的取值范围.答案：(],0−∞解析：偶次根号下非负，当x 的范围为R 时，20x a −≥在R 上恒成立，等价于2a x ≤在R 上恒成立求出a 的范围为0a ≤，(],0a ∴∈−∞★☆☆练习1若函数()212f x x ax a=−+ 的定义域为R ，则实数a 的取值范围. 答案：()0,1解析：分式型函数分母不为零，当x 的范围为R 时，220x ax a −+≠恒成立；2(2)40a a ∆=−−<即01a <<； 所以a 的取值范围是()0,1.知识点要点总结：一 具体函数定义域的常见类型：1.分式中分母不为零2.偶次根式非负3.零次幂底数非零4. 当题中出现多个函数的四则运算及复合时，注意考虑每一个函数定义域并取交集5. 实际问题中除考虑函数解析式有意义外，还应考虑实际问题本身的要求．二．抽象函数的定义域问题(1)若已知函数f (x )的定义域为[a ，b ]，其复合函数f (g (x ))的定义域由不等式a ≤g (x )≤b 求出；(2)若已知函数f (g (x ))的定义域为[a ，b ]，则f (x )的定义域为g (x )在x ∈[a ，b ]上的值域．二、函数的解析式【知识点】求函数解析式的四种常用方法1. 拼凑法：将等号右侧的式子拼凑成关于f 后括号内东西的表达式，然后将其直接写成x ．2. 换元法：已知复合函数(())f g x 的解析式，可用换元法，此时要注意新元的取值范围.3.待定系数法：已知函数类型．①正比例函数：(0)y kx k =≠； ②反比例函数：(0)k y k x=≠； ③一次函数：(0)y kx b k =+≠；④二次函数：2(0)y ax bx c a =++≠．4.方程组法：两个f ，将题目中的x 换成另一个括号内的东西构造方程组．比如：若给出()f x 和()f x −，或()f x 和1()f x 的一个方程，则可以x 代换x −（或1x），构造出另一个方程，解此方程组，消去()f x −（或1()f x）即可求出()f x 的表达式。

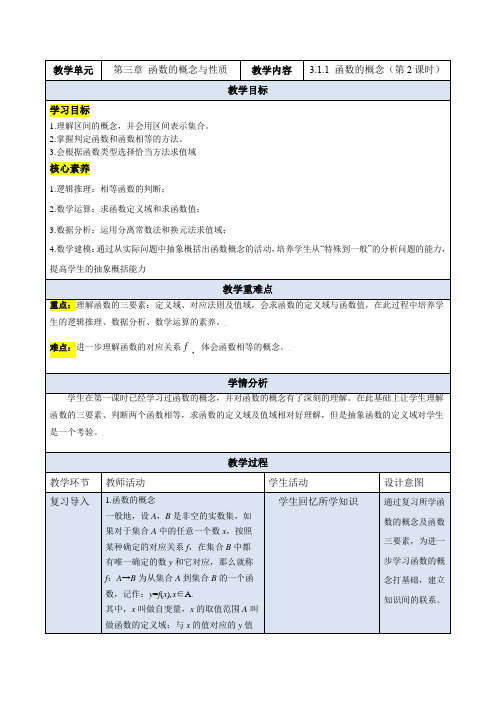
重点：理解函数的三要素：定义域、对应法则及值域，会求函数的定义域与函数值，在此过程中培养学生的逻辑推理、数据分析、数学运算的素养。

难点：进一步理解函数的对应关系f，体会函数相等的概念。

学生在第一课时已经学习过函数的概念，并对函数的概念有了深刻的理解。

在此基础上让学生理解函数的三要素、判断两个函数相等，求函数的定义域及值域相对好理解，但是抽象函数的定义域对学生是一个考验。

注意：1、区间是集合的另一种表示形
式，注意与不等式的区别。

如：x ≥－1与[－1，＋∞)是完全不同的 2、写区间的端点时，一定注意书写准确
根据具体实例结合数形结合让学
生加深对区间的
理解，使实例成
为理解概念的一
种思维载体。

【练一练】 (1)用区间表示{x |x ≥0且x ≠2}注意区间左端点
【例1】 把下列数集用区间表示： (1){x |x ≥－1}； (2){x |x <0}；
(3){x |－1<x <1}； (4){x |0<x <1或2≤x ≤4}.
；
量的值求对应的
函数值，提高学
生数学运算的核
心素养，为求函
数的值域打好基．
础。

通过函数的定义，学生自主归纳出两个函数是同一个函数的概念，培养学生数学抽象的核心素养。

通过具体的例子，使学生掌握同一函数的判断方法.
通过课堂练习，巩固本节学习的内容。

第2课时函数的定义域与值域[目标] 1.了解构成函数的要素，理解函数相等的概念；2.会求简单函数的定义域与值域；3.会求形如f(g(x))的函数的定义域．[重点] 函数相等的概念，求函数的值域．[难点] 求函数的值域，求形如f(g(x))的函数的定义域.知识点一函数相等[填一填]1．条件：①定义域相同；②对应关系完全一致．2．结论：两个函数相等．[答一答]1．若两个函数的定义域和值域相同，它们是否为同一函数？对应关系和值域相同呢？提示：观察下表：对于f1(x)和f2(x)，定义域和值域虽相同，但对应关系不同，故不是同一函数；对于f3(x)和f4(x)，对应关系和值域虽相同，但定义域不同，故不是同一函数．知识点二函数的定义域[填一填]函数的定义域是使函数有意义的所有自变量的集合．求函数的定义域时，一般遵循以下原则：1．f(x)是整式时，定义域是全体实数的集合．2．f (x )是分式时，定义域是使分母不为0的一切实数的集合． 3．f (x )是偶次根式时，定义域是使被开方式为非负值的实数的集合． 4．零(负)指数幂的底数不能为零．5．对于含字母参数的函数，求其定义域时，需根据问题的具体情况对字母参数进行讨论．6．由实际问题确定的函数，其定义域除使函数有意义外，还要符合问题的实际意义．[答一答]2．函数f (x )＝x －1x －2＋(x －1)0的定义域为( D ) A ．{x |x ≥1} B ．{x |x >1}C ．{x |1≤x <2或x >2}D ．{x |1<x <2或x >2}解析：要使函数有意义，则只需⎩⎪⎨⎪⎧x －1≥0，x －2≠0，x －1≠0，解得1<x <2或x >2，所以函数的定义域为{x |1<x <2或x >2}．故选D.知识点三 函数的值域[填一填]求函数的值域是一个较复杂的问题，要首先明确两点：一是值域的概念，即对于定义域A 上的函数y ＝f (x )，其值域就是指其函数值的集合：{f (x )|x ∈A }；二是函数的定义域、对应关系是确定函数的依据．另外，在求函数的值域时，要根据所给的函数的形式，采用相应的方法．[答一答]3．已知函数y ＝x 2，x ∈{0,1,2，－1}，函数y ＝x 2的值域是什么？提示：当x ＝0时，y ＝0；当x ＝±1时，y ＝1；当x ＝2时，y ＝4.所以函数的值域是{0,1,4}．类型一 函数相等的判断[例1] 下列各组函数： ①f (x )＝x 2－xx ，g (x )＝x －1；②f (x )＝x x ，g (x )＝x x； ③f (x )＝x ＋1·1－x ，g (x )＝1－x 2； ④f (x )＝(x ＋3)2，g (x )＝x ＋3；⑤汽车匀速运动时，路程与时间的函数关系f (t )＝80t (0≤t ≤5)与一次函数g (x )＝80x (0≤x ≤5)．其中表示相等函数的是____________(填上所有正确的序号)． [答案] ③⑤[解析] ①不同，定义域不同，f (x )定义域为{x |x ≠0}，g (x )定义域为R .②不同，对应法则不同，f (x )＝1x，g (x )＝x .③相同，定义域、对应法则都相同．④不同，值域不同，f (x )≥0，g (x )∈R .⑤相同，定义域、对应法则都相同．讨论函数问题时，要保持定义域优先的原则.判断两个函数是否相等，要先求定义域，若定义域不同，则不相等；若定义域相同，再化简函数的解析式，若解析式相同，则相等，否则不相等.[变式训练1] 下列各组中两个函数是否表示相等函数？ (1)f (x )＝6x ，g (x )＝63x 3； (2)f (x )＝x 2－9x －3，g (x )＝x ＋3；(3)f (x )＝x 2－2x －1，g (t )＝t 2－2t －1.解：(1)g (x )＝63x 3＝6x ，它与f (x )＝6x 定义域相同，对应关系也相同，所以是相等函数． (2)f (x )＝x 2－9x －3＝x ＋3(x ≠3)，它与g (x )＝x ＋3的定义域不同，故不是相等函数．(3)虽然自变量用不同的字母表示，但两个函数的定义域和对应关系都相同，故是相等函数．类型二 函数的定义域 命题视角1：求具体函数的定义域[例2] 求下列函数的定义域，结果用区间表示： (1)y ＝x ＋2＋1x 2－x －6；(2)y ＝(x ＋1)0|x |－x .[解] (1)要使函数有意义，则有⎩⎪⎨⎪⎧ x ＋2≥0，x 2－x －6≠0⇒⎩⎪⎨⎪⎧x ≥－2，x ≠－2且x ≠3，故函数的定义域是(－2,3)∪(3，＋∞)．(2)要使函数有意义，必须满足⎩⎪⎨⎪⎧x ＋1≠0，|x |－x >0，解得⎩⎪⎨⎪⎧x ≠－1，x <0，故函数的定义域是(－∞，－1)∪(－1,0)．求函数的定义域就是求使函数式有意义的自变量的取值范围.当一个函数式由两个以上数学式子的和、差、积、商的形式构成时，定义域是使各部分都有意义的公共部分的集合.[变式训练2] 求下列函数的定义域： (1)y ＝1－x ＋1x ＋5；(2)y ＝31－1－x.解析：(1)由已知得⎩⎪⎨⎪⎧1－x ≥0，x ＋5≠0，解得x ≤1且x ≠－5.所求定义域为{x |x ≤1且x ≠－5}．(2)由已知得⎩⎪⎨⎪⎧1－x ≥0，1－1－x ≠0，解得x ≤1且x ≠0.所求定义域为{x |x ≤1且x ≠0}．命题视角2：求抽象函数的定义域[例3] (1)已知函数f (x )的定义域是[－1,4]，求函数f (2x ＋1)的定义域． (2)已知函数f (2x ＋1)的定义域是[－1,4]，求函数f (x )的定义域．[分析] 在对应关系相同的情况下， f (x )中x 应与f (g (x ))中g (x )的取值范围相同，据此可解答该题．[解] (1)由已知f (x )的定义域是[－1,4]， 即－1≤x ≤4.故对于f (2x ＋1)应有－1≤2x ＋1≤4. ∴－2≤2x ≤3，∴－1≤x ≤32.∴f (2x ＋1)的定义域是⎣⎡⎦⎤－1，32. (2)由已知f (2x ＋1)的定义域是[－1,4]，即f (2x ＋1)中，应有－1≤x ≤4，∴－1≤2x ＋1≤9. ∴f (x )的定义域是[－1,9]．因为f (g (x ))就是用g (x )代替了f (x )中的x ，所以g (x )的取值范围与f (x )中的x 的取值范围相同.若已知函数f (x )的定义域为[a ，b ]，则函数f (g (x ))的定义域是指满足不等式a ≤g (x )≤b 的x 的取值范围；而已知f (g (x ))的定义域是[a ，b ]，指的是x ∈[a ，b ]，要求f (x )的定义域，就是求x ∈[a ，b ]时g (x )的值域.[变式训练3] 若函数y ＝f (x )的定义域是[0,2]，则函数g (x )＝f (2x )x －1的定义域是( B )A ．[0,1]B ．[0,1)C ．[0,1)∪(1,4]D ．(0,1)解析：因为f (x )的定义域为[0,2]，所以对于函数g (x )满足0≤2x ≤2，且x ≠1，故x ∈[0,1)．类型三 求函数的值域[例4] 求下列函数的值域． (1)f (x )＝3x －1，x ∈[－5,2)； (2)y ＝2x ＋1，x ∈{1,2,3,4,5}； (3)y ＝x 2－4x ＋6，x ∈[1,5)；(4)y ＝5x －14x ＋2.[解] (1)∵x ∈[－5,2)，∴－15≤3x <6，∴－16≤3x －1<5，∴函数f (x )＝3x －1，x ∈[－5,2)的值域是[－16,5)． (2)∵x ∈{1,2,3,4,5}，∴2x ＋1∈{3,5,7,9,11}，即所求函数的值域为{3,5,7,9,11}． (3)y ＝x 2－4x ＋6＝(x －2)2＋2.∵x ∈[1,5)，∴其图象如图所示， 当x ＝2时，y ＝2；当x ＝5时，y ＝11. ∴所求函数的值域为[2,11)． (4)y ＝5x －14x ＋2＝54(4x ＋2)－1－1044x ＋2＝54(4x ＋2)－1444x ＋2＝54－72(4x ＋2).∵72(4x ＋2)≠0，∴y ≠54，∴函数y ＝5x －14x ＋2的值域为{y ∈R |y ≠54}．根据函数关系式，选择恰当的方法求函数的值域.(1)对于一次函数，已知自变量的取值范围，依据简单不等式的运算，求得函数的取值范围，即为函数的值域；(2)对于二次函数，可借助图象求函数的值域；(3)通过分离常数，借助反比例函数的特征求值域.无论哪种方法求值域，都应注意定义域的限制.[变式训练4] 求下列函数的值域： (1)y ＝2x ＋1，x ∈{0,1,3,4}； (2)y ＝xx ＋1；(3)y ＝x 2－4x ，x ∈[1,4]． 解：(1)∵y ＝2x ＋1，x ∈{0,1,3,4}， ∴y ∈{1,3,7,9}．(2)∵y ＝xx ＋1＝(x ＋1)－1x ＋1＝1－1x ＋1，且1x ＋1≠0， ∴函数y ＝xx ＋1的值域为{y |y ≠1}．(3)配方，得y ＝(x －2)2－4. ∵x ∈[1,4]，∴函数的值域为[－4,0].1．函数f (x )＝x ＋1＋12－x的定义域为( A ) A ．[－1,2)∪(2，＋∞) B ．(－1，＋∞) C ．[－1,2)D ．[－1，＋∞)解析：由⎩⎪⎨⎪⎧x ＋1≥0，2－x ≠0，解得x ≥－1且x ≠2.故选A.2．函数f (x )＝x 2＋1(0<x ≤2且x ∈N *)的值域是( D ) A ．{x |x ≥1} B ．{x |x >1} C ．{2,3}D ．{2,5}解析：∵0<x ≤2且x ∈N *， ∴x ＝1或x ＝2. ∴f (1)＝2，f (2)＝5， 故函数的值域为{2,5}．3．若函数f (x )与g (x )＝32－x －2是相等的函数，则函数f (x )的定义域是[2,6)∪(6，＋∞)．解析：∵2－x －2≠0，∴x ≠6，又x －2≥0，∴x ≥2，∴g (x )的定义域为[2,6)∪(6，＋∞)． 故f (x )的定义域是[2,6)∪(6，＋∞)．4．已知函数f (x )的定义域为{x |－1<x <1}，则函数f (2x ＋1)的定义域为{x |－1<x <0}． 解析：因为f (x )的定义域为{x |－1<x <1}， 所以－1<2x ＋1<1，解得－1<x <0.所以f (2x ＋1)的定义域为{x |－1<x <0}． 5．试求下列函数的定义域与值域： (1)f (x )＝(x －1)2＋1； (2)y ＝5x ＋4x －1；(3)y ＝x －x ＋1.解：(1)函数的定义域为R ，因为(x －1)2＋1≥1，所以函数的值域为{y |y ≥1}． (2)函数的定义域为{x |x ≠1}，y ＝5x ＋4x －1＝5＋9x －1，所以函数的值域为{y |y ≠5}．(3)要使函数式有意义，需x ＋1≥0，即x ≥－1，故函数的定义域为{x |x ≥－1}．设t ＝x ＋1，则x ＝t 2－1(t ≥0)，于是y ＝t 2－1－t ＝(t －12)2－54，又t ≥0，故y ≥－54，所以函数的值域为{y |y ≥－54}．——本课须掌握的三大问题1．两个函数当且仅当它们的三要素完全相同时才表示同一函数，根据它们之间的关系，判断两个函数是否为同一函数，主要看它们的定义域和对应法则是否相同．因为只要定义域相同，对应法则相同，则值域就相同．2．研究函数问题必须树立“定义域优先”原则．求函数定义域一般有三种类型：(1)函数来自实际问题的定义域；(2)已知函数解析式求定义域；(3)抽象函数求定义域．3．求值域的方法有：(1)观察法：根据定义域和对应关系求出；(2)数形结合法：作出函数的图象，然后求解；(3)配方法：配方求解；(4)分离常数法：添一项、减一项，分离出常数再求解；(5)换元法：可以将无理函数转换成有理函数再求解．学习至此，请完成课时作业7 学科素养培优精品微课堂 复合函数与抽象函数开讲啦 1.复合函数的概念如果函数y ＝f (t )的定义域为A ，函数t ＝g (x )的定义域为D ，值域为C ，则当C ⊆A 时，称函数y ＝f (g (x ))为f (t )与g (x )在D 上的复合函数，其中t 叫做中间变量，t ＝g (x )叫做内层函数，y ＝f (t )叫做外层函数．2．抽象函数的概念没有给出具体解析式的函数，称为抽象函数． 3．抽象函数或复合函数的定义域理解抽象函数或复合函数的定义域，要明确以下几点： (1)函数f (x )的定义域是指x 的取值范围．(2)函数f (φ(x ))的定义域是指x 的取值范围，而不是φ(x )的范围．(3)f (t )，f (φ(x ))，f (h (x ))三个函数中的t ，φ(x )，h (x )在对应关系f 下的范围相同． [典例] 若函数f (x )的定义域为[0,1]，求g (x )＝f (x ＋m )＋f (x －m )(m >0)的定义域． [解] ∵f (x )的定义域为[0,1]，∴g (x )＝f (x ＋m )＋f (x －m )中自变量x 需满足⎩⎪⎨⎪⎧ 0≤x ＋m ≤1，0≤x －m ≤1，解得⎩⎪⎨⎪⎧－m ≤x ≤1－m ，m ≤x ≤1＋m .当1－m ＝m ，即m ＝12时，x ＝12；当1－m >m ，即0<m <12时，如图1，m ≤x ≤1－m .当1－m <m ，即m >12时，如图2，x ∈∅.综上所述，当0<m <12时，g (x )的定义域为[m,1－m ]；当m ＝12时，g (x )的定义域为⎩⎨⎧⎭⎬⎫12；当m >12时，函数g (x )的定义域为∅.[对应训练] 已知函数f (x ＋3)的定义域为[－4,5]，则函数f (2x －3)的定义域为⎣⎡⎦⎤1，112. 解析：∵函数f (x ＋3)的定义域为[－4,5]，∴－4≤x ≤5，∴－1≤x ＋3≤8，即函数f (x )的定义域为[－1,8]．由－1≤2x －3≤8，解得1≤x ≤112.故函数f (2x －3)的定义域为⎣⎡⎦⎤1，112.。

第2课时 函数相等复 习1.函数的概念.2.函数的定义域的求法.导入新课思路1.当实数a 、b 的符号相同,绝对值相等时,实数a=b;当集合A 、B 中元素完全相同时,集合A=B;那么两个函数满足什么条件才相等呢？引出课题:函数相等.思路2.我们学习了函数的概念,y=x 与y=xx 2是同一个函数吗？这就是本节课学习的内容,引出课题:函数相等.推进新课新知探究提出问题①指出函数y=x+1的构成要素有几部分？②一个函数的构成要素有几部分？③分别写出函数y=x+1和函数y=t+1的定义域和对应关系,并比较异同.④函数y=x+1和函数y=t+1的值域相同吗？由此可见两个函数的定义域和对应关系分别相同,值域相同吗？⑤由此你对函数的三要素有什么新的认识？讨论结果：①函数y=x+1的构成要素为:定义域R ,对应关系x→x+1,值域是R.②一个函数的构成要素为:定义域、对应关系和值域,简称为函数的三要素.其中定义域是函数的灵魂,对应关系是函数的核心.当且仅当两个函数的三要素都相同时,这两个函数才相同. ③定义域和对应关系分别相同.④值域相同.⑤如果两个函数的定义域和对应关系分别相同,那么它们的值域一定相等.因此只要两个函数的定义域和对应关系分别相同,那么这两个函数就相等.应用示例思路11.下列函数中哪个与函数y=x 相等？ (1)y=(x )2;(2)y=33x ;(3)y=2x ;(4)y=x x 2. 活动：让学生思考两个函数相等的条件后,引导学生求出各个函数的定义域,化简函数关系式为最简形式.只要它们定义域和对应关系分别相同,那么这两个函数就相等.解：函数y=x 的定义域是R ,对应关系是x→x.(1)∵函数y=(x )2的定义域是［0,+∞),∴函数y=(x )2与函数y=x 的定义域R 不相同.∴函数y=(x )2与函数y=x 不相等.(2)∵函数y=33x 的定义域是R , ∴函数y=33x 与函数y=x 的定义域R 相同. 又∵y=33x =x,∴函数y=33x 与函数y=x 的对应关系也相同. ∴函数y=33x 与函数y=x 相等.(3)∵函数y=2x 的定义域是R ,∴函数y=2x 与函数y=x 的定义域R 相同.又∵y=2x =|x|,∴函数y=2x 与函数y=x 的对应关系不相同.∴函数y=2x 与函数y=x 不相等. (4)∵函数y=xx 2的定义域是(-∞,0)∪(0,+∞), ∴函数y=xx 2与函数y=x 的定义域R 不相同, ∴函数y=(x )2与函数y=x 不相等.点评：本题主要考查函数相等的含义.讨论函数问题时,要保持定义域优先的原则.对于判断两个函数是否是同一个函数,要先求定义域,若定义域不同,则不是同一个函数;若定义域相同,再化简函数的解析式,若解析式相同(即对应关系相同),则是同一个函数,否则不是同一个函数. 变式训练判断下列各组的两个函数是否相同,并说明理由.①y=x-1,x ∈R 与y=x-1,x ∈N ;②y=4-x 2与y=2-x ·2x +;③y=1+x 1与u=1+x1; ④y=x 2与y=x 2x ;⑤y=2|x|与y=⎩⎨⎧<-≥;0,2,0,2x x x x ⑥y=f(x)与y=f(u).是同一个函数的是________(把是同一个函数的序号填上即可).解：只需判断函数的定义域和对应法则是否均相同即可.①前者的定义域是R ,后者的定义域是N ,由于它们的定义域不同,故不是同一个函数;②前者的定义域是{x|x≥2或x≤-2},后者的定义域是{x|x≥2},它们的定义域不同,故不是同一个函数;③定义域相同均为非零实数,对应法则相同都是自变量取倒数后加1,那么值域必相同,故是同一个函数;④定义域是相同的,但对应法则不同,故不是同一个函数;⑤函数y=2|x|=⎩⎨⎧<-≥,0,2,0,2x x x x 则定义域和对应法则均相同,那么值域必相同,故是同一个函数;⑥定义域相同,对应法则相同,那么值域必相同,故是同一个函数.故填③⑤⑥.思路21.判断下列函数f(x)与g(x)是否表示同一个函数,说明理由.(1)f(x)=(x-1)0,g(x)=1. (2)f(x)=x-1,g(x)=12x -x 2+.(3)f(x)=x 2,g(x)=(x+1)2.(4)f(x)=x 2-1,g(u)=u 2-1.活动：学生思考函数的概念及其三要素,教师引导学生先判断定义域是否相同,当定义域相同时,再判断它们的对应关系是否相同.解：(1)∵f(x)=(x-1)0的定义域是{x|x≠1},函数g(x)=1的定义域是R ,∴函数f(x)=(x-1)0与函数g(x)=1的定义域不同.∴函数f(x)=(x-1)0与函数g(x)=1不表示同一个函数.(2)∵f(x)=x-1的定义域是R ,g(x)=12x -x 2+=21)-(x 的定义域是R , ∴函数f(x)=x-1与函数g(x)=12x -x 2+的定义域相同.又∵g(x)=12x -x 2+=21)-(x =|x-1|, ∴函数f(x)=x-1与函数g(x)=12x -x 2+的对应关系不同.∴函数f(x)=x-1与函数g(x)=12x -x 2+不表示同一个函数.(3)很明显f(x)=x 2和g(x)=(x+1)2的定义域都是R ,又∵f(x)=x 2和g(x)=(x+1)2的对应关系不同,∴函数f(x)=x 2和g(x)=(x+1)2不表示同一个函数.(4)很明显f(x)=x 2-1与g(u)=u 2-1的定义域都是R ,又∵f(x)=x 2-1与g(u)=u 2-1的对应关系也相同,∴函数f(x)=x 2-1与g(u)=u 2-1表示同一个函数.变式训练1.2007湖北黄冈模拟,理13已知函数f(x)满足f(ab)=f(a)+f(b)且f(2)=p,f(3)=q,则f(36)=_______. 解：由题意得f(36)=f(6×6)=f(6)+f(6)=2f(6)=2f(2×3)=2［f(2)+f(3)］=2p+2q.答案：2p+2q2.函数y=f(x)的图象与直线x=2的公共点共有( )A.0个B.1个C.0个或1个D.不确定答案：C2.设y 是u 的函数y=f(u),而u 又是x 的函数u=g(x),设M 表示u=g(x)的定义域,N 是函数y=f(u)的值域,当M∩N≠∅时,则y 成为x 的函数,记为y=f[g(x)].这个函数叫做由y=f(u)及u=g(x)复合而成的复合函数,它的定义域为M∩N,u 叫做中间变量,f 称为外层函数,g 称为内层函数.指出下列复合函数外层函数和内层函数,并且使外层函数和内层函数均为基本初等函数. (1)y=11+x ;(2)y=(x 2-2x+3)2;(3)y=x x112+-1. 活动：让学生思考有哪些基本初等函数,它们的解析式是什么. 解：(1)设y=u 1,u=x+1, 即y=11+x 的外层函数是反比例函数y=u1,内层函数是一次函数u=x+1. (2)设y=u 2,u=x 2-2x+3,即y=(x 2-2x+3)2的外层函数是二次函数y=u 2,内层函数是二次函数u=x 2-2x+3.(3)设y=u 2+u-1,u=x 1, 即y=xx 112+-1的外层函数是二次函数y=u 2+u-1,内层函数是反比例函数u=x 1. 点评：到目前为止,我们所遇到的函数大部分是复合函数,并且是由正、反比例函数和一、二次函数复合而成的,随着学习的深入,我们还会学习其他复合函数.复合函数是高考重点考查的内容之一,应引起我们的重视.变式训练1.2004重庆高考,文2设f(x)=1122+-x x ,则)21()2(f f =_______. 答案：-12.2006安徽高考,理15函数f(x)对任意实数x 满足条件f(x+2)=)(1x f ,若f(1)=-5,则f ［f(5)］=.分析:∵函数f(x)对任意实数x 满足条件f(x+2)=)(1x f ,∴f(x+4)=f ［(x+2)+1］=)2(1+x f =f(x). ∴f(1)=f(1+4)=f(5).又∵f(1)=-5,∴f(5)=-5.∴f ［f(5)］=f(-5)=f(-5+4)=f(-1)=f(-1+4)=f(3)=f(1+2)=)1(1f =51-. 答案：51-知能训练1.下列给出的四个图形中,是函数图象的是( )A.①B.①③④C.①②③D.③④图1-2-1-2答案：B2.函数y=f(x)的定义域是R ,值域是［1,2］,则函数y=f(2x-1)的值域是_______.答案：［1,2］3.下列各组函数是同一个函数的有________.①f(x)=3x ,g(x)=x x ;②f(x)=x 0,g(x)=01x ; ③f(x)=u 2-,g(u)=u2-;④f(x)=-x 2+2x,g(u)=-u 2+2u. 答案：②③④拓展提升问题:函数y=f(x)的图象与直线x=m 有几个交点？探究:设函数y=f(x)定义域是D,当m ∈D 时,根据函数的定义知f(m)唯一,则函数y=f(x)的图象上横坐标为m 的点仅有一个(m,f(m)),即此时函数y=f(x)的图象与直线x=m 仅有一个交点;当m D 时,根据函数的定义知f(m)不存在,则函数y=f(x)的图象上横坐标为m 的点不存在,即此时函数y=f(x)的图象与直线x=m 没有交点.综上所得,函数y=f(x)的图象与直线x=m 有交点时仅有一个,或没有交点.课堂小结(1)复习了函数的概念,总结了函数的三要素;(2)学习了复合函数的概念;(3)判断两个函数是否是同一个函数.作业1.设M={x|-2≤x≤2},N={y|0≤y≤2},给出下列4个图形,其中能表示以集合M 为定义域,N 为值域的函数关系是( )图1-2-1-3分析:A 中,当0<x≤2时,N 中没有元素与x 对应,不能构成函数关系;C 中一个x 有两个y 与之对应,所以不是函数关系;D中,表示函数关系,但是表示的函数值域不是N.答案：B2.某公司生产某种产品的成本为1000元,以1100元的价格批发出去,随生产产品数量的增加,公司收入_______,它们之间是关系________.分析:由题意,多生产一单位产品则多收入100元.生产产品数量看成是自变量,公司收入看成是因变量,容易得出对于自变量的每一个确定值,因变量都有唯一确定值与之对应,从而判断两者是函数关系.答案：增加函数3.函数y=x2与S=t2是同一函数吗?答:函数的确定只与定义域与对应关系有关,而与所表示的字母无关,因此y=x2与S=t2表示的是同一个函数.因此并非字母不同便是不同的函数,这是由函数的本质决定的.设计感想本节教学内容主要是依据高考说明,对课本内容适当拓展,重点对函数的相等问题进行了引申,设计时对拓展的内容采取渐进式,设计时本着逐步提高、拓展,不能急于求成,否则事倍功半.。