12.3.2 角的平分线的判定 练习

人教版数学八年级上册12．3.2角的平分线的判定培优训练一．选择题（本大题共10小题，每小题3分，共30分）1．△ABC是一个任意三角形，用直尺和圆规作出∠A，∠B的平分线，如果两条平分线交于点O，那么下列选项中不正确的是()A．点O一定在△ABC的内部B．∠C的平分线一定经过点OC．点O到△ABC三边的距离一定相等D．点O到△ABC三顶点的距离一定相等2．在正方形网格中，∠AOB的位置如图所示，到∠AOB两边距离相等的点应是()A．点M B．点NC．点P D．点Q3．△ABC是一个任意三角形，用直尺和圆规作出∠A，∠B的平分线，如果两条平分线交于点O，那么下列说法中不正确的是( )A．点O一定在△ABC的内部B．∠C的平分线一定经过点OC．点O到△ABC的三边距离一定相等D．点O到△ABC三顶点的距离一定相等4．如图，O是△ABC内一点，且O到三边AB，BC，CA的距离OF＝OD＝OE，若∠BAC＝70°，则∠BOC的度数是( )A．35°B．145°C．55°D．125°5．如图，AD⊥OB，BC⊥OA，垂足分别为D，C，AD与BC相交于点P，若PA＝PB，则∠1与∠2的大小关系是()A．∠1＝∠2 B．∠1＞∠2C．∠1＜∠2 D．无法确定6．如图，在△ABC中，∠ABC，∠ACB外角的平分线相交于点F，连接AF，则下列结论正确的是() A．AF平分BC B．AF平分∠BACC．AF⊥BC D．以上结论都正确7．如图，已知∠ABC，小彬借助一把没有刻度且等宽的直尺，按如图的方法画出了∠ABC的平分线BP.他这样做的依据是()A．在一个角的内部，且到角两边的距离相等的点在这个角的平分线上B．角的平分线上的点到这个角两边的距离相等C．三角形三条角平分线的交点到三边的距离相等D．以上均不正确8. 如图，OP是∠AOB的平分线，点C，D分别在角的两边OA，OB上，添加下列条件，不能判定△POC ≌△POD的选项是()A．PC⊥OA，PD⊥OBB．OC＝ODC．∠OPC＝∠OPD9．△ABC是一个任意三角形，用直尺和圆规作出∠A，∠B的平分线，如果两条平分线交于点O，那么下列选项中不正确的是()A．点O一定在△ABC的内部B．∠C的平分线一定经过点OC．点O到△ABC三边的距离一定相等D．点O到△ABC三顶点的距离一定相等10．如图，在四边形ABCD中，AB＝CD，BA和CD的延长线交于点E，若点P使得S△PAB＝S△PCD，则满足此条件的点P( )A．有且只有1个B．有且只有2个C．组成∠E的角平分线D．组成∠E的角平分线所在的直线(E点除外)二．填空题（共8小题，3*8=24）11. 如图，PD⊥OA，PE⊥OB，点D，E为垂足，PD＝6 cm，当PE＝___cm时，点P在∠AOB的平分线上．12．如图，DE⊥AB于点E，DF⊥BC于点F，且DE＝DF，若∠DBC＝50°，则∠ABC＝______°.13．如图，点P在∠AOB内部，PC⊥OA于点C，PD⊥OB于点D，PC＝3 cm，当PD＝____cm时，P点在∠AOB的平分线上．14．在△ABC中，点D在BC边上，DE⊥AB于点E，DF⊥AC于点F，DE＝DF，∠B＝50°，∠C ＝70°，那么∠DAF＝________，∠ADE＝_______．15．如图，已知△ABC的周长是20，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD＝3，△ABC的面积是___．16．如图，O是△ABC内的一点，且O到△ABC的三边AB，BC，CA的距离OF＝OD＝OE，若∠A ＝70°，则∠BOC＝_________．17．如图，OP平分∠MON，PE⊥OM于点E，PF⊥ON于点F，OA＝OB，则图中有____对全等三角形．18．直线l1，l2，l3表示三条两两相互交叉的公路，现在拟建一个货物中转站，要求它到三条公路的距离都相等，则可供选择的地址有____处．三．解答题（共9小题，66分）19．(6分)如图，∠ABC的平分线与∠ACB的外角平分线相交于点D，连接AD.求证：AD是∠BAC 的外角平分线．20．(6分) 如图，BD＝CD，BF⊥AC于点F，CE⊥AB于点E.求证：点D在∠BAC的角平分线上．21．(6分) 如图，PA＝PB，∠1＋∠2＝180°，求证：OP平分∠AOB.22．(6分) 如图，∠ABC的角平分线与∠ACB的外角平分线相交于点D，连接AD.求证：AD是∠BAC的外角平分线．23．(6分) 如图，D，E，F分别是△ABC三边上的点，CE＝BF，△DCE和△DBF的面积相等．求证：AD平分∠BAC.24．(8分) 已知点O到△ABC的两边AB，AC所在直线的距离相等，且OB＝OC.(1)如图①，若点O在边BC上，求证：∠ABC＝∠ACB；(2)如图②，若点O在△ABC的内部，∠OBC＝∠OCB，求证：∠ABC＝∠ACB；(3)若点O在△ABC的外部，则∠ABC＝∠ACB成立吗？请画图表示．25．(8分) 如图，在四边形ABDC中，∠D＝∠B＝90°，点O为BD的中点，且OA平分∠BAC.(1)求证：OC平分∠ACD；(2)求证：OA⊥OC；(3)求证：AB＋CD＝AC.参考答案：1-5DADDA 6-10BADDD11. 612. 10013. 314. 30°，60°15. 3016. 125°17. 318. 419. 解：过点D分别作DE⊥AB，DG⊥AC，DF⊥BC，垂足分别为点E，G，F.又∵BD平分∠ABC，CD平分∠ACF，∴DE＝DF，DG＝DF，∴DE＝DG，∴AD平分∠EAC，即AD是∠BAC的外角平分线20. 解：∵CE⊥AB于E，BF⊥AC于F，∴∠BED＝∠CFD＝90°，又∵∠EDB＝∠CDF，BD＝CD，∴△BED≌△CFD(AAS)，∴ED＝DF，∴点D在∠BAC的角平分线上21. 解：过点P作PE⊥AO，PF⊥OB，垂足分别为E，F，∵∠1＋∠2＝180°，∠2＋∠PBO＝180°，∴∠1＝∠PBO，在△PAE和△PBF中，∠AEP＝∠BFP，∠1＝∠PBF，PA＝PB，∴△PAE≌△PBF，∴PE＝PF，∴OP平分∠AOB22. 解：过点D分别作DE⊥AB，DG⊥AC，DF⊥BC，垂足分别为E，G，F，∵BD平分∠ABC，CD平分∠ACF，∴DE＝DF，DG＝DF，∴DE＝DG，∴AD平分∠EAC.即AD是∠BAC的外角平分线∵S △DCE ＝12CE·DG ，S △DBF ＝12BF·DH ，S △DCE ＝S △DBF ， ∴12CE·DG ＝12BF·DH.又∵CE ＝BF ，∴DG ＝DH ， ∴点D 在∠BAC 的平分线上，即AD 平分∠BAC24. 解：(1)过点O 分别作OE ⊥AB ，OF ⊥AC ，E ，F 分别为垂足，则OE ＝OF ， 在Rt △OEB 和Rt △OFC 中，OB ＝OC ，OE ＝OF ，∴Rt △OEB ≌Rt △OFC(HL)，∴∠ABC ＝∠ACB(2)过点O 分别作OE ⊥AB ，OF ⊥AC ，E ，F 分别为垂足，则OE ＝OF ，由HL 可证Rt △OEB ≌Rt △OFC ，∴∠OBE ＝∠OCF ，∵∠OBC ＝∠OCB ，∴∠ABC ＝∠ACB(3)不一定成立，如图25. 解：(1)过点O 作OE ⊥AC 于E ，∵∠B ＝90°，OA 平分∠BAC.∴OB ＝OE ，∵点O 为BD 的中点，∴OB ＝OD ，∴OE ＝OD ，∵∠D ＝90°，∴OC 平分∠ACD(2)在Rt △ABO 和Rt △AEO 中，∵AO ＝AO ，OB ＝OE ，∴Rt △ABO ≌Rt △AEO(HL)，∴∠AOB ＝∠AOE.同理，∠COD ＝∠COE ，∴∠AOC ＝∠AOE ＋∠COE ＝12×180°＝90°， ∴OA ⊥OC(3)∵Rt △ABO ≌Rt △AEO ，∴AB ＝AE ，同理可得CD ＝CE ，。

12.3角的平分线的性质—2023-2024学年人教版数学八年级上册堂堂练1.如图,OP平分,于点A,,点Q是射线OM上的一个动点,则下列结论正确的是( )A. B. C. D.2.如图，在中，，以顶点A为圆心，适当长度为半径画弧，分别交AC、AB于点M、N，再分别以点M、N为圆心，大于的长度为半径画弧，两弧交于点P，作射线AP交BC于点D，若，，则的面积是( )A.15B.30C.45D.603.角平分线的作法（尺规作图）①以点O为圆心，任意长为半径画弧，交OA、OB于C、D两点；②分别以C、D为圆心，大于CD长为半径画弧，两弧交于点P；③过点P作射线OP，射线OP即为所求.角平分线的作法依据的是( )A.SSSB.SASC.AASD.ASA4.如图，在中，，AD平分，交BC于点D．已知，，则的面积为( )A.80B.40C.20D.105.如图，的三边AB，BC，CA长分别是20，30，40，其三条角平分线将分为三个三角形，则等于( )A. B. C. D.6.如图，，，若，，则D到AB的距离为________。

7.如图，直线a，b，c表示3条互相交叉的公路.若要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的站址有______________处.8.如图，，M是BC的中点，DM平分，求证：AM平分.答案以及解析1.答案：C解析:平分,于点A,点P到OM的距离等于线段PA的长度,当时,PQ有最小值,的最小值,,即,故选C2.答案：C解析：如图，作于点E，由题意知AD是的角平分线，，，，的面积，故选C.3.答案：A解析：如下图所示：连接CP、DP，在与中，由作图可知：，，故选A.4.答案：B解析：如图，作于E，，，，故选B.5.答案：C解析：过点O作于D，于E，于F，点O是内心，，，故选C.6.答案： 4.解析：作于E，，，，，，，，故答案为：4．7.答案：4解析：如图，根据角平分线的性质定理，可知内部有1个点，另外与的平分线的交点、与的平分线的交点、与的平分线的交点，共4处站址可供选择.8.解析：如图，过点M作于F，，DM平分，，M是BC的中点，，，又，点M在的平分线上，AM平分.。

2018年秋八年级数学上册第十二章《全等三角形》12.3 角的平分线的性质12.3.2 角的平分线的判定课时作业（新版）新人教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018年秋八年级数学上册第十二章《全等三角形》12.3 角的平分线的性质12.3.2 角的平分线的判定课时作业（新版）新人教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018年秋八年级数学上册第十二章《全等三角形》12.3 角的平分线的性质12.3.2 角的平分线的判定课时作业（新版）新人教版的全部内容。

第2课时角的平分线的判定知识要点基础练知识点1角的平分线的判定1。

如图，DB⊥AB,DC⊥AC，BD=DC,∠BAC=80°,则∠BAD=(B)A.10°B.40°C。

30° D.20°2。

在正方形网格中,∠AOB的位置如图所示,到两边距离相等的点应是（C）A。

C点 B.D点C.E点D。

F点3.如图，△OPD和△OPE是两个直角三角形，PD=3 cm，当PE=3 cm时,OP平分∠AOB.知识点2角的平分线的实际应用4。

如图，已知∠ABC，小彬借助一把没有刻度且等宽的直尺，按如图的方法画出了∠ABC的平分线BP。

他这样做的依据是（A)A。

在一个角的内部，且到角两边的距离相等的点在这个角的平分线上B.角平分线上的点到这个角两边的距离相等C。

三角形三条角平分线的交点到三条边的距离相等D.以上选项都不对5.如图,要在河流的右侧、公路的左侧M区处建一个工厂,位置选在到河流和公路的距离相等,并且到河流与公路交叉A处的距离为1 cm（指图上距离)的地方,则图中工厂的位置应选在哪里?并说明理由.解：工厂的位置应选在∠A的平分线上，且到点A的距离为1 cm的地方.理由：角平分线上的点到角的两边的距离相等.知识点3角平分线与三角形的结合6.如图所示是一块三角形的草坪,现要在草坪上建一个凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在(B)A。

专题12.3 角的平分线的性质1.角平分线的定义将一个已知的角平分为两个相等的角的射线叫做这个已知角的平分线。

2.作角平分线（尺规作图，四弧一线）角平分线的作法（尺规作图）①以点O为圆心，任意长为半径画弧，交OA、OB于C、D两点；②分别以C、D为圆心，大于CD长为半径画弧，两弧交于点P；③过点P作射线OP，射线OP即为所求．3.角平分线的性质定理：角平分线上的点到角的两边的距离相等。

符号语言：∵OP平分∠AOB，AP⊥OA，BP⊥OB，∴AP=BP.4.角平分线性质定理的逆定理：到角的两边距离相等的点在角的平分线上。

符号语言：∵AP⊥OA，BP⊥OB，AP=BP，∴点P在∠AOB的平分线上.5.角平分线的综合应用（1）为推导线段相等、角相等提供依据和思路；（2）实际生活中的应用．6.证明命题基本方法（1）明确命题中的已知和求（包括隐含条件，如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形等所隐含的边角关系）（2）根据题意，画出图形，并用数字符号表示已知和求证.（3）经过分析，找出由已知推出求证的途径，写出证明过程.【例题1】已知：OC平分∠MON，P是OC上任意一点，PA⊥OM，PB⊥ON，垂足分别为点A、点B．求证：PA＝PB．【答案】见解析。

【解析】证明：∵PA⊥OM，PB⊥ON∴∠PAO＝∠PBO＝90°∵OC平分∠MON∴∠1＝∠2在△PAO和△PBO中，∴△PAO≌△PBO∴PA＝PB【例题2】已知：点P是∠MON内一点，PA⊥OM于A，PB⊥ON于B，且PA＝PB．求证：点P在∠MON的平分线上．【答案】见解析。

【解析】证明：连结OP在Rt△PAO和Rt△PBO中，PA=PB OP=OP∴Rt△PAO≌Rt△PBO（HL）∴∠1＝∠2∴OP平分∠MON即点P在∠MON的平分线上．【例题3】已知：如图，在R t△ABC中，∠C＝90°，D是AC上一点，DE⊥AB于E，且DE＝DC．（1）求证：BD平分∠ABC；（2）若∠A＝36°，求∠DBC的度数．【答案】见解析。

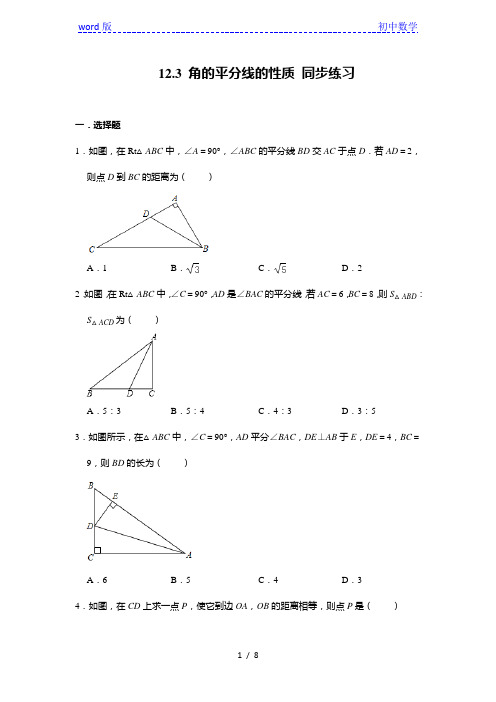
12.3 角的平分线的性质同步练习一．选择题1．如图，在Rt△ABC中，∠A＝90°，∠ABC的平分线BD交AC于点D．若AD＝2，则点D到BC的距离为（）A．1 B．C．D．22．如图，在Rt△ABC中，∠C＝90°，AD是∠BAC的平分线，若AC＝6，BC＝8，则S△ABD：S△ACD为（）A．5：3 B．5：4 C．4：3 D．3：53．如图所示，在△ABC中，∠C＝90°，AD平分∠BAC，DE⊥AB于E，DE＝4，BC＝9，则BD的长为（）A．6 B．5 C．4 D．34．如图，在CD上求一点P，使它到边OA，OB的距离相等，则点P是（）A．线段CD的中点B．CD与过点O作CD的垂线的交点C．CD与∠AOB的平分线的交点D．以上均不对5．点P在∠AOB的平分线上，点P到OA边的距离等于m，点Q是OB边上的一个动点，则PQ与m的大小关系是（）A．PQ＜m B．PQ＞m C．PQ≤m D．PQ≥m6．如图，在△ABC中，∠ACB的外角平分线与∠ABC的外角平分线相交于点D．则下列结论正确的是（）A．AD平分BC B．AD平分∠CAB C．AD平分∠CDB D．AD⊥BC7．如图在△ABC中，∠ACB＝90°，BE平分∠ABC，DE⊥AB于D，如果△ADE的周长为6cm，AC＝4cm，那么AD等于（）A．2cm B．4cm C．3cm D．6cm8．如图，点O在△ABC内，且到三边的距离相等．若∠A＝40°，则∠BOC等于（）A．110°B．115°C．125°D．130°9．如图，∠MON＝60°．①以点O为圆心，2cm长为半径画弧，分别交OM、ON于点A、C；②在分别以A、C为圆心，2cm长为半径画弧，两弧交于点B；③连结AB、BC，则四边形OABC的面积为（）A．4cm2B．2cm2C．4cm2D．2cm210．如图，四边形ABDC中，对角线AD平分∠BAC，∠ACD＝136°，∠BCD＝44°，则∠ADB的度数为（）A．54°B．50°C．48°D．46°二．填空题11．如图，在Rt△ABC中，∠ACB＝90°，AD平分∠BAC交BC于点D，若AB＝5，DC ＝2，则△ABD的面积为．12．如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于点E，DF⊥AC于点F，若△ABC的面积为21cm2，AB＝8cm，AC＝6cm，则DE的长为cm．13．如图，点E在∠BOA的平分线上，EC⊥OB，垂足为C，点F在OA上，若∠AFE ＝30°，EC＝3，则EF＝．14．如图，若BD⊥AE于B，DC⊥AF于C，且DB＝DC，∠BAC＝40°，∠ADG＝130°，则∠DGF＝．15．如图，已知在△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB交BC于点D，DE⊥AB 于点E，AB＝8cm，那么△DEB的周长是cm．三．解答题16．如图，已知CD是△ABC的角平分线，DE⊥BC，垂足为E，若AC＝4，BC＝10，△ABC的面积为14，求DE的长．17．如图，点P是∠MON中一点，P A⊥OM于点A，PB⊥ON于点B，连接AB，∠P AB ＝∠PBA．求证：OP平分∠MON．18．如图，在△ABC中，AD平分∠BAC，∠C＝90°，DE⊥AB于点E，点F在AC上，BD＝DF．（1）求证：CF＝EB．（2）若AB＝12，AF＝8，求CF的长．参考答案1．D2．A3．B4．C5．D6．B7．A8．A9．B10．D11．512．313．614．150°15．816．解：过点D作DF⊥AC交CA的延长线于点F，如图，∵CD平分∠ACB，DE⊥BC于E，∴DF＝DE．∵△ABC的面积为14，∴S△BCD+S△ACD＝14，∴×DE×10+×DF×4＝14，即5DE+2DE＝14，∴DE＝2．17．证明：∵∠P AB＝∠PBA，∴P A＝PB，∵P A⊥OM于点A，PB⊥ON于点B，∴OP平分∠MON．18．（1）证明：∵AD平分∠BAC，∠C＝90°，DE⊥AB于E，∴DE＝DC．在△CDF与△EDB中，，∴Rt△CDF≌Rt△EDB（HL），∴CF＝EB．（2）解：设CF＝x，则AE＝12﹣x，∵AD平分∠BAC，DE⊥AB，∴CD＝DE．在△ACD与△AED中，，∴△ACD≌△AED（HL），∴AC＝AE，即8+x＝12﹣x，解得x＝2，即CF＝2．。

第2课时角的平分线的判定习题角的平分线是将一个角分成两个相等的角的线段。

角的平分线的判定方法有以下几种：1.利用三角形内角和定理：对于一个三角形ABC，如果角BAD的平分线BE与边AC重合，则角BAD等于角DAE，即角BAD的平分线BE将角BAD分成两个相等的角。

2.利用垂直平分线的性质：如果有一条线段AD垂直于一条线段BC，并且将角ABC分成两个相等的角，则线段AD是角ABC的平分线。

3.利用角的外切圆：对于一个三角形ABC，如果角BAD的平分线BE与角ABC的外切圆相切于点E，则角BAD的平分线BE将角ABC分成两个相等的角。

下面是一些角的平分线的判定习题及其答案：习题1：在△ABC中，角BAD的平分线BE与边AC重合，证明角BAD等于角DAE。

解答：由平分线的定义可知，角BAD的平分线BE将角BAD分成两个相等的角。

又因为平分线BE与边AC重合，所以角BAD等于角DAE。

习题2：在△ABC中，角BAD的平分线BE与边AC相交于点D，且角BAD等于角DAE，证明BE是角ABC的平分线。

解答：由角BAD等于角DAE可知，角BAD的平分线BE将角BAD分成两个相等的角。

又因为角BAD的平分线BE与边AC相交于点D，所以BE将角ABC分成两个相等的角，即BE是角ABC的平分线。

习题3：在△ABC中，角BAD的平分线BE与角ABC的外切圆相切于点E，证明角BAD等于角DAE。

解答：由平分线的定义可知，角BAD的平分线BE将角BAD分成两个相等的角。

又因为角BAD的平分线BE与角ABC的外切圆相切于点E，所以角BAD等于角DAE。

习题4：在△ABC中，角BAD的平分线BE与角ABC的外切圆相切于点E，证明BE是角ABC的平分线。

解答：由角BAD的平分线BE与角ABC的外切圆相切于点E可知，角BAD的平分线BE将角ABC分成两个相等的角。

所以BE是角ABC的平分线。

12.3 角的平分线的性质专题一利用角的平分线的性质解题1．如图，在△ABC中，AC=AB，D在BC上，若DF⊥AB，垂足为F，DG⊥AC，垂足为G，且DF=DG．求证：AD⊥BC.2．如图，已知CD⊥AB于点D，BE⊥AC于点E，BE，CD交于点O，且AO平分∠BAC．求证：OB=OC．3．如图，在Rt△ABC中，∠C=90°，21BAC B∠∠，AD是∠∶∶BAC的角平分线，DE⊥AB于点E，AC=3 cm，求BE的长．专题二角平分线的性质在实际生活中的应用4．如图，三条公路把A、B、C三个村庄连成一个三角形区域，某地区决定在这个三角形区域内修建一个集贸市场，要使集贸市场到三条公路的距离相等，则这个集贸市场应建在（）A．在AC、BC两边高线的交点处B．在AC、BC两边中线的交点处C．在∠A、∠B两内角平分线的交点处D．在AC、BC两边垂直平分线的交点处5．如图，要在河流的南边，公路的左侧M区处建一个工厂，位置选在到河流和公路的距离相等，并且到河流与公路交叉A处的距离为1cm（指图上距离），则图中工厂的位置应在__________，理由是__________．6．已知：有一块三角形空地，若想在空地中找到一个点，使这个点到三边的距离相等，试找出该点．（保留作图痕迹）状元笔记【知识要点】1．角的平分线的性质角的平分线上的点到角的两边的距离相等．2．角的平分线的判定角的内部到角的两边的距离相等的点在角的平分线上．【温馨提示】1．到三角形三边距离相等的点是三角形三条角平分线的交点，不是其他线段的交点．2．到三角形三边距离相等的点不仅有内角的平分线的交点，还有相邻两外角的平分线的交点，这样的点共有4个．【方法技巧】1．利用角的平分线的性质解决问题的关键是：挖掘角的平分线上的一点到角两边的垂线段．若已知条件存在两条垂线段——直接考虑垂线段相等，若已知条件存在一条垂线段——考虑通过作辅助线补出另一条垂线段，若已知条件不存在垂线段——考虑通过作辅助线补出两条垂线段．2．利用角平分线的判定解决问题的策略是：挖掘已知图形中一点到角两边的垂线段．若已知条件存在两条垂线段——先证明两条垂线段相等，然后说明角平分线或角的关系；若已知条件存在一条垂线段——考虑通过作辅助线补出另一条垂线段，再证明两条垂线段相等；若已知条件不存在垂线段——考虑通过作辅助线补出两条垂线段后，证明两条垂线段相等．参考答案:1．证明：∵DF AB DG AC DF DG ⊥⊥=，，，∴AD 是BAC ∠的平分线，∴BAD CAD =∠∠．在ABD △和ACD △中，⎪⎩⎪⎨⎧=∠=∠=（公共边）（已求）已知）AD AD DAC DAB AC AB (∴SAS)ABD ACD (△≌△．∴ADB ADC =∠∠．又∵180BDA CDA +=︒∠∠，∴90BDA =︒∠，∴AD BC ⊥．2．证明：∵AO 平分∠BAC ，OD ⊥AB ，OE ⊥AC ，∴OD =OE ，在Rt △BDO 和Rt △CEO 中，⎪⎩⎪⎨⎧∠=∠=∠=∠,,COE DOB OEOD CEO BDO∴(ASA)BDO CEO △≌△．∴OB =OC ．3．解：∵∠C =90°，∴∠BAC +∠B =90°，又DE ⊥AB ，∴∠C =∠AED =90°，又21BAC B =∶∶∠∠，∴∠A =60°，∠B =30°，又∵AD 平分∠BAC ，DC ⊥AC ，DE ⊥AB ，∴DC =DE ，∴3AE AC ==cm ．在Rt △DAE 和Rt △DBE 中，⎪⎩⎪⎨⎧=∠=∠∠=∠.DE DE BEDAED B DAE∴△DAE ≌△DBE （AAS ），∴3BE AE == cm ．4．C 解析：根据角平分线的性质，集贸市场应建在∠A 、∠B 两内角平分线的交点处．故选C ．5．∠A 的角平分线上，且距A1cm 处 角平分线上的点到角两边的距离相等6．解：作两个角的平分线，交点P 就是所求作的点．人教版七年级上册期末测试卷一、选择题(每题3分，共30分)1．某天的最高气温是8℃，最低气温是－3℃，那么这天的温差是( )A．－3℃B．8℃C．－8℃D．11℃2．下列立体图形中，从上面看能得到正方形的是( )3．下列方程是一元一次方程的是( )A．x－y＝6 B．x－2＝xC．x2＋3x＝1 D．1＋x＝34．今年某市约有108 000名应届初中毕业生参加中考，108 000用科学记数法表示为( )A．0.108×106B．10.8×104C．1.08×106D．1.08×1055．下列计算正确的是( )A．3x2－x2＝3 B．3a2＋2a3＝5a5C ．3＋x ＝3xD ．－0.25ab ＋14ba ＝0 6．已知ax ＝ay ，下列各式中一定成立的是( )A ．x ＝yB ．ax ＋1＝ay －1C ．ax ＝－ayD ．3－ax ＝3－ay7．某商品每件标价为150元，若按标价打8折后，再降价10元销售，仍获利10%，则该商品每件的进价为( )A ．100元B ．105元C ．110元D ．120元8．如果一个角的余角是50°，那么这个角的补角的度数是( )A ．130°B ．40°C ．90°D ．140°9．如图，C ，D 是线段AB 上的两点，点E 是AC 的中点，点F 是BD 的中点，EF ＝m ，CD ＝n ，则AB 的长是( )A ．m －nB ．m ＋nC ．2m －nD ．2m ＋n10．下列结论： ①若a ＋b ＋c ＝0，且abc ≠0，则a ＋c 2b ＝－12； ②若a ＋b ＋c ＝0，且a ≠0，则x ＝1一定是方程ax ＋b ＋c ＝0的解；③若a ＋b ＋c ＝0，且abc ≠0，则abc ＞0；④若|a |>|b |，则a －b a ＋b>0. 其中正确的结论是( )A ．①②③B ．①②④C ．②③④D ．①②③④二、填空题(每题3分，共24分)11．－⎪⎪⎪⎪⎪⎪⎪⎪－23的相反数是________，－15的倒数的绝对值是________．12．若－13xy 3与2x m －2y n ＋5是同类项，则n m ＝________. 13．若关于x 的方程2x ＋a ＝1与方程3x －1＝2x ＋2的解相同，则a 的值为________．14．一个角的余角为70°28′47″，那么这个角等于____________．15．下列说法：①两点确定一条直线；②两点之间，线段最短；③若∠AOC ＝12∠AOB ，则射线OC 是∠AOB 的平分线；④连接两点之间的线段叫做这两点间的距离；⑤学校在小明家南偏东25°方向上，则小明家在学校北偏西25°方向上，其中正确的有________个．16．在某月的月历上，用一个正方形圈出2×2个数，若所圈4个数的和为44，则这4个日期中左上角的日期数值为________．17．规定一种新运算：a△b＝a·b－2a－b＋1，如3△4＝3×4－2×3－4＋1＝3.请比较大小：(－3)△4________4△(－3)(填“>”“＝”或“<”)．18．如图是小明用火柴棒搭的1条“金鱼”、2条“金鱼”、3条“金鱼”……则搭n条“金鱼”需要火柴棒__________根．三、解答题(19，20题每题8分，21～23题每题6分，26题12分，其余每题10分，共66分)19．计算：(1)－4＋2×|－3|－(－5)；(2)－3×(－4)＋(－2)3÷(－2)2－(－1)2 018.20．解方程：(1)4－3(2－x)＝5x；(2)x －22－1＝x ＋13－x ＋86.21．先化简，再求值：2(x 2y ＋xy )－3(x 2y －xy )－4x 2y ，其中x ＝1，y ＝－1.22．有理数b 在数轴上对应点的位置如图所示，试化简|1－3b |＋2|2＋b |－|3b －2|.23．如图①是一些小正方体所搭立体图形从上面看得到的图形，方格中的数字表示该位置的小正方体的个数．请在如图②所示的方格纸中分别画出这个立体图形从正面看和从左面看得到的图形．24．已知点O是直线AB上的一点，∠COE＝90°，OF是∠AOE 的平分线．(1)当点C，E，F在直线AB的同侧时(如图①所示)，试说明∠BOE＝2∠COF.(2)当点C与点E，F在直线AB的两侧时(如图②所示)，(1)中的结论是否仍然成立？请给出你的结论，并说明理由．25．为鼓励居民节约用电，某市电力公司规定了电费分段计算的方法：每月用电不超过100度，按每度电0.50元计算；每月用电超过100度，超出部分按每度电0.65元计算．设每月用电x度．(1)当0≤x≤100时，电费为________元；当x>100时，电费为____________元．(用含x的整式表示)(2)某用户为了解日用电量，记录了9月前几天的电表读数．该用户9月的电费约为多少元？(3)该用户采取了节电措施后，10月平均每度电费0.55元，那么该用户10月用电多少度？26．如图，O为数轴的原点，A，B为数轴上的两点，点A表示的数为－30，点B表示的数为100.(1)A，B两点间的距离是________．(2)若点C也是数轴上的点，点C到点B的距离是点C到原点O的距离的3倍，求点C表示的数．(3)若电子蚂蚁P从点B出发，以6个单位长度/s的速度向左运动，同时另一只电子蚂蚁Q恰好从点A出发，以4个单位长度/s的速度向左运动，设两只电子蚂蚁同时运动到了数轴上的点D，那么点D表示的数是多少？(4)若电子蚂蚁P从点B出发，以8个单位长度/s的速度向右运动，同时另一只电子蚂蚁Q恰好从点A出发，以4个单位长度/s的速度向右运动．设数轴上的点N到原点O 的距离等于点P到原点O的距离的一半(点N在原点右侧)，有下面两个结论：①ON＋AQ的值不变；②ON－AQ的值不变，请判断哪个结论正确，并求出正确结论的值．(第26题)答案一、1.D 2.A 3.D 4.D 5.D 6.D7．A 8.D 9.C 10.B二、11.23；5 12.－8 13.－514．19°31′13″15.3 16.717．> 18.(6n＋2)三、19.解：(1)原式＝－4＋2×3＋5＝－4＋6＋5＝7；(2)原式＝12＋(－8)÷4－1＝12－2－1＝9.20．解：(1)去括号，得4－6＋3x＝5x.移项、合并同类项，得－2x＝2.系数化为1，得x＝－1.(2)去分母，得3(x－2)－6＝2(x＋1)－(x＋8)．去括号，得3x－6－6＝2x＋2－x－8.移项、合并同类项，得2x＝6.系数化为1，得x＝3.21．解：原式＝2x2y＋2xy－3x2y＋3xy－4x2y＝(2x2y－3x2y－4x2y)＋(2xy＋3xy)＝－5x2y＋5xy.当x＝1，y＝－1时，原式＝－5x2y＋5xy＝－5×12×(－1)＋5×1×(－1)＝5－5＝0.22．解：由题图可知－3<b<－2.所以1－3b>0，2＋b<0，3b－2<0.所以原式＝1－3b－2(2＋b)＋(3b－2)＝1－3b－4－2b＋3b－2＝－2b－5.23．解：如图所示．24．解：(1)设∠COF＝α，则∠EOF＝90°－α.因为OF是∠AOE的平分线，所以∠AOE＝2∠EOF＝2(90°－α)＝180°－2α.所以∠BOE＝180°－∠AOE＝180°－(180°－2α)＝2α.所以∠BOE＝2∠COF.(2)∠BOE＝2∠COF仍成立．理由：设∠AOC＝β，则∠AOE＝90°－β，又因为OF是∠AOE的平分线，所以∠AOF＝90°－β2.所以∠BOE＝180°－∠AOE＝180°－(90°－β)＝90°＋β，∠COF＝∠AOF＋∠AOC＝90°－β2＋β＝12(90°＋β)．所以∠BOE＝2∠COF.25．解：(1)0.5x；(0.65x－15)(2)(165－123)÷6×30＝210(度)，210×0.65－15＝121.5(元)．答：该用户9月的电费约为121.5元．(3)设10月的用电量为a度．根据题意，得0.65a－15＝0.55a，解得a＝150.答：该用户10月用电150度．26．解：(1)130(2)若点C在原点右边，则点C表示的数为100÷(3＋1)＝25；若点C在原点左边，则点C表示的数为－[100÷(3－1)]＝－50.故点C表示的数为－50或25.(3)设从出发到同时运动到点D经过的时间为t s，则6t －4t＝130，解得t＝65.65×4＝260，260＋30＝290，所以点D表示的数为－290.(4)ON－AQ的值不变．设运动时间为m s，则PO＝100＋8m，AQ＝4m. 由题意知N为PO的中点，得ON＝12PO＝50＋4m，所以ON＋AQ＝50＋4m＋4m＝50＋8m，ON－AQ＝50＋4m－4m＝50.故ON－AQ的值不变，这个值为50.。

人教版八年级数学上册12.3角平分线的性质课时训练（含答案）人教版八年级数学上册12.3 角平分线的性质课时训练一、选择题1. 如图，PD⊥AB，PE⊥AC，垂足分别为D，E，且PD＝PE，则△APD与△APE 全等的理由是()A．SAS B．AAA C．SSS D．HL2. 如图，P是∠AOB的平分线OC上一点，PD⊥OA，垂足为D.若PD＝2，则点P到边OB的距离是()A．4 B. 3 C．2 D．13. 如图，P为OC上一点，PM⊥OA，PN⊥OB，垂足分别为M，N，PM＝PN，∠BOC＝30°，则∠AOB的度数为()A．30°B．45°C．60°D．50°4. 下面是黑板上给出的尺规作图题，需要回答横线上符号代表的内容．已知∠AOB.求作：∠AOB的平分线．作法如下：①以点O为圆心，适当长为半径画弧，交OA于点M，交__○__于点N；②分别以点__⊕__为圆心，大于__△__的长为半径画弧，两弧在__?__的内部交于点C；③画射线OC，OC即为所求．则下列回答正确的是()A．○表示OA B．⊕表示M，CC．△表示MN D．?表示∠AOB5. 如图，在直角坐标系中，AD是Rt△OAB的角平分线，点D的坐标是(0，-3)，那么点D到AB的距离是()A.3B.-3C.2D.-26. 如图,利用尺规作∠AOB的平分线OC,其作法如下:(1)以点O为圆心,适当长为半径画弧,与OA,OB分别交于点D,E;(2)分别以点D,E为圆心,大于DE的长为半径画弧,两弧在∠AOB的内部交于点C;(3)画射线OC,则射线OC就是∠AOB的平分线.这样作图的原理是三角形全等的一种判定方法,这种判定方法是()A.SSSB.SASC.ASAD.AAS7. 如图,AB∥CD,以点A为圆心,小于AC的长为半径画弧,与AB,AC分别交于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧在∠CAB的内部交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC 的大小是()A.20°B.25°C.30°D.40°8. 如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于12MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D.若CD＝4，AB＝16，则△ABD的面积是()A．14 B．32 C．42 D．569. 如图，已知在四边形ABCD中，∠BCD＝90°，BD平分∠ABC，AB＝6，BC ＝9，CD＝4，则四边形ABCD的面积是()A．24 B．30C．36 D．4210. 如图,AD是△ABC的角平分线,DE⊥AB,AB=6 cm,DE=4 cm,S△ABC=30 cm2,则AC的长为()A.10 cmB.9 cmC.4.5 cmD.3 cm二、填空题11. 如图，OP为∠AOB的平分线，PC⊥OB于点C，且PC＝3，点P到OA的距离为________．12. 如图,在△ABC中,两条外角平分线交于点P,PM⊥AC交AC的延长线于点M.若PM=6 cm,则点P到AB的距离为.13. 将两块完全相同的三角尺在∠AOB的内部如图摆放，两块三角尺较短的直角边分别与∠AOB的两边重合，且含30°角的顶点恰好也重合于点C，则射线OC 即为∠AOB的平分线，理由是______________________．14. 如图，∠B＝∠D＝90°，根据角平分线的性质填空：(1)若∠1＝∠2，则________＝________．(2)若∠3＝∠4，则________＝________．15. 如图,在△ABC中,E为AC的中点,AD平分∠BAC交BC于点D,AB︰AC=2︰3,AD与BE相交于点O.若△OAE的面积比△BOD的面积大1,则△ABC的面积是.三、解答题16. 育新中学校园内有一块直角三角形(Rt△ABC)空地，如图所示，园艺师傅以角平分线AD为界，在其两侧分别种上了不同的花草，在△ABD区域内种植了一串红，在△ACD区域内种植了鸡冠花，并量得两直角边AB＝20 m，AC＝10 m，分别求一串红与鸡冠花两种花草的种植面积．17. 如图，已知∠1=∠2,BA18. 如图，在∠AOB的两边OA，OB上分别取点D，M和点E，N，使OM=ON，OD=OE，DN和EM相交于点C.求证:点C在∠AOB的平分线上.19. 如图，A，B两点分别在射线OM，ON上，点C在∠MON的内部且CA＝CB，CD⊥OM，CE⊥ON，垂足分别为D，E，且AD＝BE.(1)求证：OC平分∠MON；(2)如果AO＝10，BO＝4，求OD的长．20. 如图，在Rt△ABC中，∠ACB＝90°，∠B＝60°，AD，CE是角平分线，AD 与CE相交于点F，FM⊥AB，FN⊥BC，垂足分别为M，N.求证：FE＝FD.人教版八年级数学上册12.3 角平分线的性质课时训练-答案一、选择题1. 【答案】D2. 【答案】C[解析] 如图，过点P作PE⊥OB于点E.∵P是∠AOB的平分线OC上一点，PD⊥OA，PE⊥OB，∴PE＝PD＝2.3. 【答案】C[解析] ∵点P在OC上，PM⊥OA，PN⊥OB，PM ＝PN，∴OC是∠AOB的平分线．∵∠BOC＝30°，∴∠AOB＝60°.4. 【答案】D5. 【答案】A[解析] 如图，过点D作DE⊥AB于点E.∵点D的坐标是(0，-3)，∴OD=3.∵AD是△OAB的角平分线，∴ED=OD=3，即点D到AB的距离是3.6. 【答案】A7. 【答案】A[解析] 由题意可得AH平分∠CAB.∵AB∥CD,∴∠C+∠CAB=180°,∠HAB=∠AHC.∵∠ACD=140°,∴∠CAB=40°.∵AH平分∠CAB,∴∠HAB=20°.∴∠AHC=20°.8. 【答案】B[解析] 如图，过点D作DH⊥AB于点H. 由作法得AP平分∠BAC.∵DC⊥AC，DH⊥AB，∴DH＝DC＝4.∴S△ABD＝12×16×4＝32.9. 【答案】B[解析] 过点D作DH⊥AB交BA的延长线于点H. ∵BD平分∠ABC，∠BCD＝90°，∴DH＝CD＝4.∴四边形ABCD的面积＝S△ABD＋S△BCD＝12AB·DH＋12BC·CD＝12×6×4＋12×9×4＝30.10. 【答案】B[解析] 如图,过点D作DF⊥AC于点F.∵AD是△ABC的角平分线,DE⊥AB,∴DE=DF=4.∵AB=6,∴S △ABC =S △ABD +S △ACD =×6×4+AC ×4=30, 解得AC=9(cm).故选B .二、填空题11. 【答案】3 【解析】如解图，过点P 作PD ⊥OA 于点D ，∵OP 为∠AOB 的平分线，PC ⊥OB 于点C ，∴PD ＝PC ，∵PC ＝3，∴PD ＝3，即点P 到点OA 的距离为3.12. 【答案】6 cm[解析] 如图,过点P 作PN ⊥BC 于点N ,PQ ⊥AB 交AB 的延长线于点Q.∵BP ,CP 是两条外角的平分线,PM ⊥AC ,∴PN=PM ,PQ=PN.∴PQ=PM.∵PM=6 cm,∴PQ=6 cm,即点P 到AB 的距离为6 cm .13. 【答案】角的内部到角的两边距离相等的点在角的平分线上14. 【答案】(1)BCCD (2)AB AD15. 【答案】10[解析] 如图,过点D 作DM ⊥AC 于点M ,DN ⊥AB 于点N.∵AD 平分∠BAC,DM ⊥AC ,DN ⊥AB , ∴DM=DN.∵S △ABD ︰S △ADC =BD ︰DC ,且S △ABD =·AB ·DN ,S △ADC =·AC ·DM ,∴BD ∶DC=AB ∶AC=2∶3. 设△ABC 的面积为S ,则S △ADC =S.∵E 为AC 的中点, ∴S △BEC =S.∵△OAE 的面积比△BOD 的面积大1, ∴△ADC 的面积比△BEC 的面积大1. ∴S-S=1.∴S=10.故答案为10.三、解答题16. 【答案】解：如图，过点D 作DE ⊥AB 于点E ，DF ⊥AC 于点F.∵AD 是∠BAC 的平分线，∴DE ＝DF. ∵AB ＝20 m ，AC ＝10 m ，∴S △ABC ＝12×20×10＝12×20·DE ＋12×10·DF ，解得DE ＝203(m)．∴△ACD 的面积＝12×10×203＝1003(m 2)，△ABD 的面积＝12×20×203＝2003(m 2)．故一串红的种植面积为2003 m 2，鸡冠花的种植面积为1003 m 2.17. 【答案】证明:如图,过点P 作PE ⊥BA 交BA 的延长线于点E.又∵∠1=∠2,PF ⊥BC ,∴PE=PF ,∠PEA=∠PFC=90°. 在Rt △PEA 与Rt △PFC 中,∴Rt △PEA ≌Rt △PFC (HL). ∴∠P AE=∠PCB. ∵∠P AE+∠BAP=180°, ∴∠PCB+∠BAP=180°.18. 【答案】证明:如图，过点C 作CG ⊥OA 于点G ，CF ⊥OB 于点F .在△MOE 和△NOD 中，∴△MOE ≌△NOD (SAS). ∴S △MOE =S △NOD .∴S △MOE -S 四边形ODCE =S △NOD -S 四边形ODCE ，即S △MDC =S △NEC .由三角形面积公式得DM ·CG=EN ·CF .∵OM=ON ，OD=OE ，∴DM=EN.∴CG=CF . 又∵CG ⊥OA ，CF ⊥OB ，∴点C 在∠AOB 的平分线上.19. 【答案】解：(1)证明：∵CD ⊥OM ，CE ⊥ON ，∴∠CDA ＝∠CEB ＝90°.在Rt △ACD 与Rt △BCE 中，CA ＝CB ，AD ＝BE ，∴Rt △ACD ≌Rt △BCE(HL)．∴CD＝CE.又∵CD ⊥OM ，CE ⊥ON ，∴OC 平分∠MON. (2)在Rt △ODC 与Rt △OEC 中，CD ＝CE ，OC ＝OC ，∴Rt △ODC ≌Rt △OEC. ∴OD ＝OE. 设BE ＝x.∵BO ＝4，∴OE ＝OD ＝4＋x. ∵AD ＝BE ＝x ，∴AO ＝OD ＋AD ＝4＋2x ＝10. ∴x ＝3.∴OD ＝4＋3＝7.20. 【答案】证明：如图，连接BF.∵F 是△ABC 的角平分线AD ，CE 的交点，∴BF 平分∠ABC. ∵FM ⊥AB ，FN ⊥BC ，∴FM ＝FN ，∠DNF ＝∠EMF ＝90°.∵在Rt △ABC 中，∠ACB ＝90°，∠ABC ＝60°，∴∠BAC ＝30°.∵AD 平分∠BAC ，∴∠DAC ＝12∠BAC ＝15°. ∴∠CDA ＝75°.∵CE 平分∠ACB ，∠ACB ＝90°，∴∠ACE ＝45°. ∴∠MEF ＝75°＝∠NDF. 在△DNF 和△EMF 中，∠DNF ＝∠EMF ，∠NDF ＝∠MEF ，FN ＝FM ，∴△DNF ≌△EMF(AAS)．∴FE ＝FD.。