2016年寒假学习成果检测-数学

16年七年级数学寒假作业有答案孩子们迫不及待的想在寒假畅快的玩一把，但是别忘了寒假作业哦。

小编给同学们整理发布了七年级数学寒假作业。

一、细心选一选(每题2分，共20分)1、下列图形中不可以折叠成正方体的是( )2、如图所示的立方体，如果把它展开，可以是下列图形中的( )*3、数轴上有两点A、B分别表示实数a、b，则线段AB的长度是( )A. a-bB. a+bC. │a-b│D. │a+b│4、已知线段AB，在BA的延长线上取一点C，使CA=3AB，则线段CA与线段CB之比为( )A. 3︰4B. 2︰3C. 3︰5D. 1︰25、如图所示，直线AB和CD相交于O，EO⊥AB，那么图中∠AOD 与∠AOC的关系是( )A. 对顶角B. 相等C. 互余D. 互补6、如图所示，点在直线PQ上，是的平分线，是的平分线，那么下列说法错误的是( )A. 与互余B. 与互余C. 与互补D. 与互补7、如图所示，下列条件中，不能判断l1∥l2的是( )A. ∠1=∠3B. ∠2=∠3C. ∠4=∠5D. ∠2+∠4=180°*8、如图所示是某中学七年级学生参加课外活动人数的扇形统计图，若参加舞蹈类的学生有42人，则参加球类活动的学生人数有( )A. 145人B. 147人C. 149人D. 151人*9、一个四边形切掉一个角后变成( )A. 四边形B. 五边形C. 四边形或五边形D. 三角形或四边形或五边形*10、下列说法中正确的有( )①同位角相等. ②凡直角都相等. ③一个角的余角一定比它的补角小.④在直线、射线和线段中，直线最长. ⑤两点之间的线段的长度就是这两点间的距离.⑥如果一个角的两边分别平行于另一个角的两边，则这两个角一定相等.A. 0个B. 1个C. 2个D. 3个二、仔细填一填(每题2分，共20分)11、如图所示，其中共有________对对顶角.12、，则它的余角等于________; 的补角是，则 =_______.13、如图所示，已知CB=4，DB=7，D是AC的中点，则AC=_________ .14、如图所示，AC⊥BC，CD⊥AB，点A到BC边的距离是线段_____的长，点B到CD边的距离是线段_____的长，图中的直角有_____________，∠A的余角有_______________，和∠A相等的角有__________.15、如图所示，直线AB、EF相交于点D，∠ADC=90 o ，若∠1与∠2的度数之比为1：4，则∠CDF、∠EDB的度数分别是 .*16、如图所示，已知AB∥CD，EF交AB于M交CD于F，MN⊥EF 于M，MN交CD于N，若∠BME=110 °，•则∠MND=_____. *17、如图所示，若直线a，b分别与直线c，d相交，且∠1+∠3=90°，∠2-∠3=90 °， ∠4=115°，那么∠3=__________.18、图(1)(2)是根据某地近两年6月上旬日平均气温情况绘制的折线统计图，通过观察图表，可以判断这两年6月上旬气温比较稳定的年份是。

2016学年度七年级数学寒假作业答案8.1答案问题导学问题1 问题2(1) (2) 问题3 全是错的问题探究问题1(1) (2) (3) (4) 问题2(1) (2)243 (3) 问题评价1. B2.C3.A4.(1)ab (2) (3)3,5,65.(1) (2) (3)06. (吨)8.2 幂的乘方和积的乘方(1)答案【问题导学】问题1.计算：(1) (2) (m是正整数); (3) (4)问题2.计算：(1) (2)问题3.下面的计算对不对?如果不对，应怎样改正?(1)错 (a5)2=a10; (2)错a5·a2=a7; (3)对 (x6)3=x18; (4)错(xn+1)2=x2n+2.【问题探究】问题1.(1)若4·8m·16m =29，则m= 1 .(2)如果2a=3，2b=6，2c=12，那么a、b、c的关系是 a问题2.计算：(1)(-x2)·(x3)2·x= (2)[(x-y)3]4= (3)[(103)2]4=【问题评价】1.C2.C3.计算：(1) (2) (3) (4) 4.计算：(1) (2) 5.(1)5400(2)18.2 幂的乘方和积的乘方(2)答案问题导学：问题1：(1)216，216(2)-216，-216(3)- ，- 问题2：(3)(3×2)n =3n×2n，(ab)n =an×bn 问题3: (ab)n =anbn(abc)n=anbncn问题探究:问题1. (1)(5m)3 =53m3 =125 m3(2)(-xy2)3=-x3(y2)3 =-x3y6(3)(3xy2)2= 32 x2 (y2)2 =9 x2 y4(4)(-2ab3c2)4 =(-2)4 a4 (b3)4 (c2)4=16 a4 b12 c8问题2.计算：(1) =( × ) 2000 × ( )2 =(2) =(-0.125×4) 5 × 45 =-32(3) = + -9 = -7(4) = =问题评价1.计算：(1) =- a3b3 (2) = x8y12(3) =4 × 106 (4) =(-2)3 (a3 ) 3 (y4 ) 3 =-8a9y12 2.计算：(1) =4(2) =97 =-13.若，则 -3 a3bc2;若，则 2ab2 或-2ab2.4.已知，求的值.解： =(-1)2n x2ny2n= (xn )2 (yn) 2= 52×(-2)2=25×4=1008.3 同底数幂的除法(1)问题导学1.(1)―( )5 (2)―x12 (3)27x6 (4)5x22.计算下列各式：(1) = = (2) = 9(3) = a3(4) = a303.归纳法则：同底数幂的除法：同底数幂相除，底数不变，指数相减.4.(7.9×103)×3600÷1000÷(1.0×103)=28.44倍问题探究问题1.计算：(1) (2) (3) (4) =x6 = ―a3 = a3b3 = p2m―1问题2.计算：(1) (2) = x+y = x4y6z2(3) (4) = 54m÷52m-1 = a9= 52m+1【问题评价】1.如果，则m、n的关系是m―2n=1 .2.若xm = 2，xn = 5，则x m+n = 10 ，x m-n =3.下面的计算是否正确?如有错误，请改正.(1) (错，=a4) (2) (对)(3) (错，= m4) (4) (错，= z4)4.计算：(1) (2) (3) =m20 = q6 = a4b4(4) (5) (6) =x4y = 32m-3 =m12 +m45. = =34÷43 =课题：8.3 同底数幂的除法(2)【问题导学】问题1.4,3,2,1,0，-1，-2,3,2,1,0，-1，-3问题2.①1，②1，③1，【问题探究】问题1.用小数或分数表示下列各数：(1) (2) (3) (4)0.000028问题2.计算：(1) (2) (3) (4)问题3.计算：(1)5;(2)0.0036;(3)a3(4) ;问题4.(1)x=-2;(2)x﹦-1.【问题评价】1.1; ;2.计算：(1)-1;(2)1;(3)4;(4)6.3.×;×;√;×4.(1)x≠0;(2)当x≠-5;(3)x=-4或-6.5.(1)0.01;(2) ;(3) ;(4)0.000021;6. .课题：8.3 同底数幂的除法(3)【问题导学】问题1.(1)0.00…01= ;(2) ，，，，- 。

2016年小学三年级寒假作业数学答案（含解析）重点推荐：小学生寒假安全教育小学生寒假电影2016年小学三年级寒假作业数学答案（含解析）1.用简便方法计算下列各题：①729+154+271②7999+785+215答：①原式=729+271+154=1154②原式=7999+(785+215)=89992.用简便方法计算下列各题：①8376+2538+7462+1624②997+95+548答：原式=(8376+1624)+(2538+7462)=20000原式=(997+3)+(92+548)=16403.求和：①3+4+5++99+100②4+8+12++32+36③65+63+61++5+3+1答：①原式=(3+100)times;98divide;2=5047②原式=(4+36)times;9divide;2=180③原式=(65+1)times;33divide;2=10894.用简便方法计算下列各题：① 958-596②1543+498答：①原式=958-(600-4)=958-600+4=362②原式=1543+(500-2)=1543+500-2=20415.巧算下列各题：①5000-2-4-6--98-100② 103+99+103+96+105+102+98+98+101+102答：①原式=5000-(2+4+6++98+100)=5000-(2+100)times;50divide;2=5000-2550=2450②原式=100times;10+(3+3+5+2+1+2)-(1+4+2+2) =1000+16-9=10076.求下列数据的平均数：199，202，195，201，196，201答：取200为基准数，先求和，再求平均数。

[200times;6+(2+1+1)-(1+5+4)]divide;6=(1200+4-10)divide;6=1194divide;6=199答：解答过程：①填千位亚=1。

2016学年数学寒假作业答案参考：初三年级一、选择题1.A2.D3.D4.D5.C6.B7.A8.B 9.B 10.D二、填空题11.3 12. 13.-1 14.=三、15.解：==.16.解：四、17.方程另一根为，的值为4。

18.因为a+b=2++2-=4，a-b=2+-(2-)=2，ab=(2+)(2-)=1所以=五、19.解：设我省每年产出的农作物秸杆总量为a，合理利用量的增长率是x，由题意得：30%a(1+x)2=60%a，即(1+x)2=2∴x1≈0.41，x2≈-2.41(不合题意舍去)。

∴x≈0.41。

即我省每年秸秆合理利用量的增长率约为41%。

20.解：(1)∵方程有实数根∴Δ=22-4(k+1)≥0解得k≤0，k的取值范围是k≤0(5分)(2)根据一元二次方程根与系数的关系，得x1+x2=-2, x1x2=k+1x1+x2-x1x2=-2 + k+1由已知，得 -2+ k+1lt;-1 解得 kgt;-2又由(1)k≤0 ∴ -2∵ k为整数∴k的值为-1和0. (5分)六、21. (1)由题意，得解得∴ (3分)又A点在函数上，所以，解得所以解方程组得七、22.解：(1)设宽为x米，则：x(33-2x+2)=150，解得：x1=10，x2= 7.5当x=10时，33-2x+2=15lt;18当x=7.5时，33-2x+2=20gt;18，不合题意，舍去∴鸡场的长为15米，宽为10米。

(5分)(2)设宽为x 米，则：x(33-2x+2)=200，即x2-35x+200=0Δ=(-35)2-4×2×200=1225-1600lt;0方程没有实数解，所以鸡场面积不可能达到200平方米。

(9分)(3)当0当15≤alt;20时，可以围成一个长方形鸡场;当a≥20时，可以围成两个长宽不同的长方形鸡场;(12分)八、23.(1)画图(2分)(2)证明：由题意可得：△ABD≌△ABE，△ACD≌△ACF .∴∠DAB=∠EAB ，∠DAC=∠FAC ，又∠BAC=45°，∴∠EAF=90°.又∵AD⊥BC∴∠E=∠ADB=90°∠F=∠ADC=90°.又∵AE=AD，AF=AD∴AE=AF.∴四边形AEGF是正方形. (7分)(3)解：设AD=x，则AE=EG=GF=x.∵BD=2，DC=3∴BE=2 ，CF=3∴BG=x-2，CG=x-3.在Rt△BGC中，BG2+CG2=BC2∴( x-2)2+(x-3)2=52.化简得，x2-5x-6=0解得x1=6，x2=-1(舍去)，所以AD=x=6. (12分)以上就是为大家整理的2016学年数学寒假作业答案参考：初三年级，怎么样，大家还满意吗?希望对大家的学习有所帮助，同时也祝大家学习进步，考试顺利!。

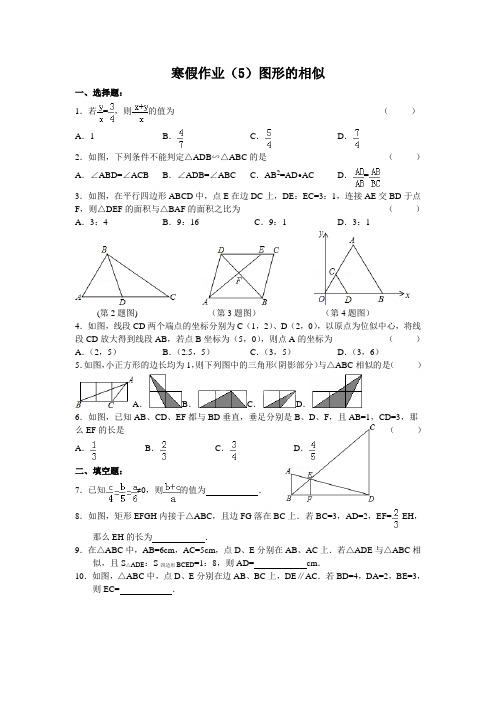
寒假作业（5）图形的相似一、选择题：1．若=，则的值为（）A．1 B．C．D．2．如图，下列条件不能判定△ADB∽△ABC的是（）A．∠ABD=∠ACB B．∠ADB=∠ABC C．AB2=AD•AC D．=3．如图，在平行四边形ABCD中，点E在边DC上，DE：EC=3：1，连接AE交BD于点F，则△DEF的面积与△BAF的面积之比为（）A．3：4 B．9：16 C．9：1 D．3：1(第2题图) （第3题图）（第4题图）4．如图，线段CD两个端点的坐标分别为C（1，2）、D（2，0），以原点为位似中心，将线段CD放大得到线段AB，若点B坐标为（5，0），则点A的坐标为（）A．（2，5）B．（2.5，5）C．（3，5）D．（3，6）5．如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是（）A．B．C．D．6．如图，已知AB、CD、EF都与BD垂直，垂足分别是B、D、F，且AB=1，CD=3，那么EF的长是（）A．B．C．D．二、填空题：7．已知≠0，则的值为．8．如图，矩形EFGH内接于△ABC，且边FG落在BC上．若BC=3，AD=2，EF=EH，那么EH的长为．9．在△ABC中，AB=6cm，AC=5cm，点D、E分别在AB、AC上．若△ADE与△ABC相似，且S△ADE：S四边形BCED=1：8，则AD=cm．10．如图，△ABC中，点D、E分别在边AB、BC上，DE∥AC．若BD=4，DA=2，BE=3，则EC=．（第8题图）（第10题图）三、解答题：11．如图，在4×3的正方形方格中，△ABC和△DEC的顶点都在边长为1的小正方形的顶点上．（1）填空：∠ABC= °，BC=（2）判断△ABC与△DEC是否相似，并证明你的结论12.如图，在直角梯形ABCD中，∠ABC=90°，AD∥BC，AD=4，AB=5，BC=6，点P是AB上一个动点，当PC+PD的和最小时，PB的长为多少？13.如图，正方形ABCD中，M为BC上一点，F是AM的中点，EF⊥AM，垂足为F，交AD的延长线于点E，交DC于点N．（1）求证：△ABM∽△EFA；（2）若AB=12，BM=5，求DE的长14.已知：△ABC在直角坐标平面内，三个顶点坐标分别为A（0，3）、B（3，4）、C（2、2）（正方形网格中每个小正方形的边长是一个单位长度）．（1）画出△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是；（2）以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是；（3）△A2B2C2的面积是多少平方单位？寒假作业（五）答案一、选择题：1.D2.D3.B4.B5.C6.C二、填空题：7.．．9.．10.．8.三、解答题：11.①135，2②△ABC与△DEC相似理由：由图可知，AB=2，ED=2∴==∵∠ABC=∠DEC=135°，∴△ABC∽△CED12. 延长CB到E，使EB=CB，连接DE交AB于P．则DE就是PC+PD的和的最小值．∵AD∥BE，∴∠A=∠PBE，∠ADP=∠E，∴△ADP∽△BEP，∴AP：BP=AD：BE=4：6=2：3，∴PB=PA，又∵PA+PB=AB=5，∴PB=AB=3．故答案为：313.（1）证明：∵四边形ABCD是正方形，∴AB=AD，∠B=90°，AD∥BC，∴∠AMB=∠EAF，又∵EF⊥AM，∴∠AFE=90°，∴∠B=∠AFE，∴△ABM∽△EFA；（2）解：∵∠B=90°，AB=12，BM=5，∴AM==13，AD=12，∵F是AM的中点，∴AF=AM=6.5，∵△ABM∽△EFA，∴，即，∴AE=16.9，∴DE=AE﹣AD=4.9．14.（1）如图所示：C 1（2，﹣2）；故答案为：（2，﹣2）；（2）如图所示：C 2（1，0）；故答案为：（1，0）；（3）∵ =20， =20， =40，∴△A 2 B 2 C 2是等腰直角三角形，∴△A 2 B 2 C 2的面积是： × × =10平方单位．故答案为：10．寒假作业(2) 圆一、选择题：1．如图，在⊙O中，直径CD垂直于弦AB，若∠C=25°，则∠BOD的度数是.......（）A．25°B．30°C．40°D．50°2．如图，已知PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P=40°，则∠BAC 的大小是（）A．70°B．40°C．50°D．20°3．一扇形的半径为60cm，圆心角为120°，用它做一个圆锥的侧面，则底面半径为（）A．5cm B. 10cm C. 20cm D. 30cm4．⊙o的半径是13，弦AB∥CD，AB=24，CD=10，则AB与CD的距离是..........（）A．7 B．17 C．7或17 D．4第1题第2题5．已知⊙O的半径为15，弦AB的长为18，点P在弦AB上且OP=13，则AP的长为（）A．4 B．14 C．4或14 D．6或146．A是半径为5的⊙O内的一点，且OA=3，则过点A且长小于10的整数弦的条数（）A．1条B．2条C．3条D．4条二、填空题：7．圆中一条弦所对的圆心角为60°，那么它所对的圆周角度数为度．8．①平分弦的直径垂直与该弦；②经过三个点一定可以作圆；③三角形的外心到三角形各顶点的距离都相等；④半径相等的两个半圆是等弧．其中正确的有．9．⊙O1和⊙O2相切，两圆的圆心距为9cm，⊙1O的半径为4cm，则⊙O2的半径为．10．如图，⊙O是△ABC的外接圆，连接OA，OB，∠OBA=48°，则∠C的度数为．11．如图，圆内一条弦CD与直径AB相交成30°角，且分直径成1cm和5cm两部分，则这条弦的弦心距是．12．如图，将△ABC绕点C旋转60°得到△A′B′C′，已知AC=6，BC=4，则线段AB扫过图形（阴影部分）的面积为．（结果保留π）第12题第13题第14题三、解答题：13．如图，AB是⊙O的弦（非直径），C、D是AB上的两点，并且AC=BD.求证：OC=OD.14．如图，四边形ABCD内接于⊙O，点E在对角线AC上，EC=BC=DC．（1）若∠CBD=39°，求∠BAD的度数；（2）求证：∠1=∠2．15．如图，在△ABC中，∠C=90°，AC+BC=8，点O是斜边AB上一点，以O为圆心的⊙O 分别与AC，BC相切于点D，E．（1）当AC=2时，求⊙O的半径；（2）设AC=x，⊙O的半径为y，求y与x的函数关系式．16．如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接PB、AB，∠PBA=∠C．（1）求证：PB是⊙O的切线；（2）连接OP，若OP∥BC，且OP=8，⊙O的半径为2，求BC的长．寒假作业（2）圆答案一．选择题:1．D．2．D．3．C．4．C．5．C．6．C．二．填空题:7．30或150．8．③④．95cm或13cm．10．42°．11．1cm ．12．．三．解答题:13．证明（略）14.（1）解：∵BC=DC，∴∠CBD=∠CDB=39°，∵∠BAC=∠CDB=39°，∠CAD=∠CBD=39°，∴∠BAD=∠BAC+∠CAD=39°+39°=78°；（2）证明：∵EC=BC，∴∠CEB=∠CBE，而∠CEB=∠2+∠BAE，∠CBE=∠1+∠CBD，∴∠2+∠BAE=∠1+∠CBD，∵∠BAE=∠CBD，∴∠1=∠2．15. 解：（1）连接OE，OD，在△ABC中，∠C=90°，AC+BC=8，∵AC=2，∴BC=6；∵以O为圆心的⊙O分别与AC，BC相切于点D，E，∴四边形OECD是正方形，tan∠B=tan∠AOD===，解得OD=，∴圆的半径为；（2）∵AC=x，BC=8﹣x，在直角三角形ABC中，tanB==，∵以O为圆心的⊙O分别与AC，BC相切于点D，E，∴四边形OECD是正方形．tan∠AOD=tanB===，解得y=﹣x2+x．16.（1）证明：连接OB，∵AC是⊙O的直径，∴∠ABC=90°，∴∠C+∠BAC=90°，∵OA=OB，∴∠BAC=∠OBA，∵∠PBA=∠C，∴∠PBA+∠OBA=90°，即PB⊥OB，∴PB是⊙O的切线；（2）解：∵⊙O的半径为2，∴OB=2，AC=4，∵OP∥BC，∴∠C=∠BOP，又∵∠ABC=∠PBO=90°，∴△ABC∽△PBO，∴，即，∴BC=2．寒假作业（3）数据与概率一、选择题：1．某气象小组测得连续五天的日最低气温并计算出平均气温与方差后，整理得出下表（有两个数据被遮盖）．第一天第二天第三天第四天第五天平均气温方差1℃﹣1℃2℃0℃■1℃■被遮盖的两个数据依次是（）A．2℃，2B．3℃，65C．3℃，2 D．2℃，852．甲、乙二人在相同条件下各射靶10次，每次射靶成绩如图所示，经计算得x甲=x乙=7，S2甲=1.2，S2乙=5.8，则下列结论中不正确的是（）A．甲、乙的总环数相等B．甲的成绩稳定C．甲、乙的众数相同D．乙的发展潜力更大3.一组数据按从小到大排列为2，4，8，x，10，14．若这组数据的中位数为9，则这组数据的众数为() A．6 B．8 C．9 D．14.一组数据：2，3，4，x 中，若中位数与平均数相等，则数x 不可能是 ( )A ．1B ．2C ．3D ．55．如图的四个转盘中，C ．D 转盘分成8等分，若让转盘自由转动一次，停止后，指针落在阴影区域内的概率最大的转盘是 （ ）A ．B ．C ．D ．6．有A 、B 两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6），以小莉掷A 立方体朝上的数字为x 、小明掷B 立方体朝上的数字为y 来确定点P （x ，y ），那么他们各掷一次所确定的点P 落在抛物线24y x x =-+上的概率为 （ ）A ．118 B ．112C ．19D ．16二、填空题：7．若x 1、x 2、x 3、x 4、x 5这5个数的方差是2，则x 1﹣1、x 2﹣1、x 3﹣1、x 4﹣1、x 5﹣1这5个数的方差是 ．8．在4张卡片上分别写有1～4的整数，随机抽取一张后放回，再随机地抽取一张，那么第二次取出的数字能够整除第一次取出的数字的概率是 ．9．箱子中装有4个只有颜色不同的球，其中2个白球，2个红球，4个人依次从箱子中任意摸出一个球，不放回，则第二个人摸出红球且第三个人摸出白球的概率是_______． 10．如果一组数据﹣2，0，3，5，x 的极差是9，那么这组数据的平均数是 ． 三、解答题：11．甲、乙两班参加学校迎“青奥”知识比赛，两班的参赛人数相等．比赛结束后，依据两分数 6分 7分 8分 9分 人数11036乙班学生迎“青奥”知识比赛成绩统计表（1）经计算乙班学生的平均成绩为7.7分，中位数为7分，请计算甲班学生的平均成绩、中位数，并从平均数和中位数的角度分析哪个班的成绩较好；（2）如果学校决定要组织6个人的代表队参加市级团体赛，为了便于管理，决定依据本次比赛成绩仅从这两个班的其中一个班中挑选参赛选手，你认为应选哪个班？请说明理由．12．甲乙两人在相同条件下各射靶10次，甲10次射靶的成绩的情况如图所示，乙10次射靶的成绩依次是：3环、4环、5环、8环、7环、7环、8环、9环、9环、10环． （1）请在图中画出乙的射靶成绩的折线图． （2）请将下表填完整：平均数方差 中位数 命中9环及以上次数 甲 7 1.2 乙4.83①从平均数和方差相结合看（分析谁的成绩稳定些）； ②从平均数和中位数相结合看（分析谁的成绩好些）．13．甲口袋中装有3个相同的小球，它们分别写有数值﹣1，2，5；乙口袋中装有3个相同的小球，它们分别写有数值﹣4，2，3．现从甲口袋中随机取一球，记它上面的数值为x ，再从乙口袋中随机取一球，记它上面的数值为y ．设点A 的坐标为（x ，y ）． （1）请用树状图或列表法表示点A 的坐标的各种可能情况； （2）求点A 落在42-+=x x y 的概率．参考答案1～6.C C D B A B 7．5 8．12 9．1310．2.6或0.4 11.解：（1）甲班学生的平均成绩为6×25%+7×20%+8×35%+9×20%=7.5（分） 甲班的中位数为（8分）由于平均数7.5＜7.7，所以从平均数来看，乙班的成绩较好； 由于中位数8＞7，所以从中位数来看，甲班的成绩较好． （2）应选乙班．因为选6人参加市级团体赛，其中乙班有6人的成绩为（9分）， 而甲班只有4人的成绩为（9分），所以应选乙班． ∴五年资助的总人数为5÷20%=25人， ∴08年资助了25﹣3﹣6﹣5﹣7=4人，∴方差为2人2，12．解：（1）如图：（2）平均数 方差 中位数 命中9环及以上次数 甲 7 1.2 7 1 乙74.87.53（3）①∵平均数相同，22S S <甲乙，∴甲的成绩比乙的成绩稳定． ②∵平均数相同，甲的中位数＜乙的中位数，乙的成绩比甲的成绩好些．13．（1）略；（2）92．寒假作业（4）二次函数一、选择题：1. 函数y=x 2-2x+3的图象的顶点坐标是( )A. (1，-4)B.(-1，2)C. (1，2)D.(0，3)2.已知函数2(3)21y k x x =-++的图象与x 轴有交点，则k 的取值范围是 ( )A ． k ＜4B ．k ≤4C. k ＜4且k ≠3D. k ≤4且k ≠33.若一次函数b ax y +=的图象经过二、三、四象限，则函数bx ax y +=2( )A. B. C. D.4.将函数2x y =的图象向左平移1个单位，再向上平移2个单位后，所得图象的函数表达O yxO yx O yx O yx式是 ( )A.2)1(2+-=x y B.2)1(2++=x y C.2)1(2--=x y D.2)1(2-+=x y5.下列函数：①x y -=；②x y =；③xy 1=；④2x y =．当0<x 时，y 随x 的增大而减小的函数有( )A ．1个B ．2个C ．3个D ．4个6.若0>b ，则二次函数12-+=bx x y 2的图象的顶点在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限 二、填空题：7. y ＝2x 2－bx ＋3的对称轴是直线x ＝1，则b 的值为__________8.已知抛物线c x ax y ++=2与x 轴交点的横坐标为1-，则c a +=_________.9.校运动会铅球比赛时，小林推出的铅球行进的高度y （米）与水平距离x （米）满足关系式为：35321212++-=x x y ，则小林这次铅球推出的距离是 米．10. 将抛物线221216y x x =-+绕它的顶点旋转180°，所得抛物线的解析式是 . 11. 已知二次函数y ＝x 2－(a ＋2)x ＋9图像的顶点在坐标轴上，则a ＝ ．12.已知实数y x y x x y x +=-++则满足,033,2的最大值为 .三、解答题：13.如果函数232(3)1m m y m x mx -+=-++是二次函数，求m 的值．14．如图，二次函数y=ax 2+bx+c 的图象经过A 、B 、C 三点．（1）观察图象，写出A 、B 、C 三点的坐标，并求出抛物线解析式； （2）求此抛物线的顶点坐标和对称轴；（3）当m 取何值时，ax 2+bx+c=m 有两个不相等的实数根．15.如图，直角△ABC 中，∠C=90°，，，点P 为边BC 上一动点，PD ∥AB ，PD 交AC 于点D ，连接AP ． （1）求AC 、BC 的长；（2）设PC 的长为x ，△ADP 的面积为y ．当x 为何值时，y 最大，并求出最大值．16．如图，已知关于x 的二次函数y ＝x 2＋mx 的图像经过原点O ，并且与x 轴交于点A ，对称轴为 直线x ＝1．（1）常数m ＝ ，点A 的坐标为 ；（2）若关于x 的一元二次方程x 2＋mx ＝n （n 为常数）有两个不相等的实数根，求n 的取值范围；（3）若关于x 的一元二次方程x 2＋mx －k ＝0（k 为常数）在－2＜x ＜3的范围内有解，求k 的取值范围．17.如图，已知抛物线y=（x ﹣2）（x+a ）（a ＞0）与x 轴交于点B 、C ，与y 轴交于点E ，且点B 在点C 的左侧．（1）若抛物线过点M （﹣2，﹣2），求实数a 的值； （2）在（1）的条件下，解答下列问题； ①求出△BCE 的面积；②在抛物线的对称轴上找一点H ，使CH+EH 的值最小，直接写出点H 的坐标．OyxA二次函数复习参考答案一、选择题：1~6 C B C B C D二、填空题：7．4 8．1 9．10 10．y=-2x2+12x-20 11．4或-8或-2 12．4三、解答题：13．解：根据二次函数的定义：m2﹣3m+2=2，且m﹣3≠0，解得：m=0．14．解：（1）由题意得：A、B、C三点的坐标分别为：（﹣1，0）、（0，﹣3）、（4，5）；设该二次函数的解析式为：y=ax2+bx+c，由题意得：，解得：a=1，b=﹣2，c=﹣3，∴该抛物线解析式为：y=x2﹣2x﹣3．（2）由（1）知：y=x2﹣2x﹣3=（x﹣1）2﹣4，∴该抛物线的顶点坐标为（1，﹣4），对称轴为x=1．（3）由题意得：x2﹣2x﹣3=m，即x2﹣2x﹣3﹣m=0①，若该方程组有两个不相等的实数根，则必有△=（﹣2）2﹣4×1×（﹣3﹣m）＞0，解得：m＞﹣4．即当m＞﹣4时，ax2+bx+c=m有两个不相等的实数根．15．解：（1）在Rt△ABC中，，，得，∴AC=2，根据勾股定理得：BC=4；（3分）（2）∵PD∥AB，∴△ABC∽△DPC，∴；设PC=x，则，，∴∴当x=2时，y的最大值是1．16．解：（1）m=-2，A(2,0)；（2）n＞-1．（3）-1≤k＜817．解：（1）将M（﹣2，﹣2）代入抛物线解析式得：﹣2=（﹣2﹣2）（﹣2+a），解得：a=4；（2）①由（1）抛物线解析式y=（x﹣2）（x+4），当y=0时，得：0=（x﹣2）（x+4），解得：x1=2，x2=﹣4，∵点B在点C的左侧，∴B（﹣4，0），C（2，0），当x=0时，得：y=﹣2，即E（0，﹣2），∴S△BCE=×6×2=6；②由抛物线解析式y=（x﹣2）（x+4），得对称轴为直线x=﹣1，根据C与B关于抛物线对称轴直线x=﹣1对称，连接BE，与对称轴交于点H，即为所求，设直线BE解析式为y=kx+b，将B（﹣4，0）与E（0，﹣2）代入得：，解得：，∴直线BE解析式为y=﹣x﹣2，将x=﹣1代入得：y=﹣2=﹣，则H（﹣1，﹣）．寒假作业（6）三角函数与货比三家一、选择题：1.sin60°的相反数是（）A.12- B.3322.在Rt△ABC中，∠C=900，AC=4，AB=5，则sinB的值是（）A.23B.35C.34D.453.把△ABC三边的长度都扩大为原来的3倍，则锐角A的正弦函数值（）A．不变 B．缩小为原来的13C．扩大为原来的3倍 D．不能确定第4题图第6题图4.在2015年的体育中考中，某校6名学生的体育成绩统计如图，则这组数据的众数、中位数、方差依是()A.18，18，1B.18，17.5，3C.18，18，3D.18，17.5，15.下列说法中不正确的是( )A.抛掷一枚硬币，硬币落地时正面朝上是随机事件B.把4个球放入三个抽屉中，其中一个抽屉中至少有2个球是必然事件C.任意打开七年级下册数学教科书，正好是97页是确定事件D.一只盒子中有白球m个，红球6个，黑球n个(每个球除了颜色外都相同).如果从中任取一个球，取得的是红球的概率与不是红球的概率相同，那么m与n的和是66.如图，为测量某物体AB的高度，在D点测得A点的仰角为30º，朝物体AB方向前进20米到达点C，再次测得A点的仰角为60º，则物体的高度为（）A.103米B.10米C.203米D.203二、填空题：7.计算cos 60º=__________; sin45°=_________.8.在Rt △ABC 中,∠C=900,AB=6,cosB=23,则BC 的长为___________.9.如图所示，△ABC 的顶点是正方形网格的格点，则sinA 的值为__________.10.如图，在边长相同的小正方形组成的网格中，点A 、B 、C 、D 都在这些小正方形的顶点上，AB 、CD 相交于点P ，则tan ∠APD 的值是 ．11.如图所示，机器人从A 点沿着西南方向行了42个单位，到达B 点后观察到原点O 在它的南偏东60°的方向上，则原来A 点的坐标为___________.(结果保留根号）．三、解答题：12.计算：（1）︒⋅︒-︒-︒+︒30tan 60tan 45tan 60cos 30sin （2）11|12|2sin 45---+︒13.如图所示，在△ABC 中，AD 是BC 边上的高，DAC B ∠=cos tan . （1）求证：AC ＝BD ; （2）若121312sin ==BC C ，，求AD 的长.14.如图，某校教学楼AB 的后面有一建筑物CD ，当光线与地面的夹角是22°时，教学楼在建筑物的墙上留下高2米的影子CE ；而当光线与地面夹角是45°时，教学楼顶A 在地面上的影子F 与墙角C 有13米的距离（B 、F 、C 在一条直线上）(1)求教学楼AB 的高度；(2)学校要在A 、E 之间挂一些彩旗，请你求出A 、E 之间的距离（结果保留整数）.（参考数据：sin22°≈38，cos22°≈1516，tan22°≈25）15.如图所示，电路图上有四个开关A ，B ，C ，D 和一个小灯泡，闭合开关D 或同时闭合开关A ，B ，C 都可以使小灯泡发光.CBA(1)任意闭合其中一个开关，则小灯泡发光的概率等于 ；(2)任意闭合其中两个开关，请用画树状图或列表的方法求出小灯泡发光的概率.16.如图，直线PQ 与⊙O 相交于点A 、B ，BC 是⊙O 的直径，BD 平分∠CBQ 交⊙O 于点D ，过点D 作DE⊥PQ，垂足为E ． （1）求证：DE 与⊙O 相切；（2）连结AD ，己知BC=10，BE=2，求sin ∠BAD 的值．寒假作业（6）答案一、选择题：1-6:C D A A A C 二、填空题：7.21 , 22 ;8.4; 9. 55; 10.2; 11.40,343⎛⎫+ ⎪⎝⎭12．（1）-1 （2）3213．(1)证明略 (2)8 14．(1)12(2)2715.（1）P=O.25 (2)P=0.516.证明：（1）连结OD ，则OD=OB, ∴∠OBD=∠ODB. ∵BD 平分∠CBQ ， ∴∠OBD=∠DBQ. ∵ DE ⊥PQ , ∴∠BED=90°.∴ ∠EBD + ∠BDE = 90°. ∴ ∠EDB + ∠BDO = 90°. 即：∠ODE = 90°.∴ DE ⊥OD , ∴DE 是⊙O 的切线. （2）连结CD ， 则∠CDB = 90°=∠BED, ∵ ∠CBD =∠DBE.∴ △CBD ∽△DBE.∴BC BDBD BE=即：2BD =BC ·BE=10×2=20, ∴ BD=25∴DE=4, ∴AB=6, ∴AE=8, ∴sin ∠BAD=55寒假作业（1） 一元二次方程一、选择题:1.方程()()1132=-+x x 的解的情况是（ ）A ．有两个不相等的实数根B ．没有实数根C ．有两个相等的实数根D ．有一个实数根2.若关于x 的一元二次方程的两个根为11x =，22x =，则这个方程是（ ） A.2320x x +-=B.2320x x -+=C.2230x x -+=D.2320x x ++=3.以3、4为两边长的三角形的第三边长是方程040132=+-x x 的根，则这个三角形的周长为（ ）A.15或12B.12C.15D.以上都不对 4.关于x 的方程220x ax a -+=的两根的平方和是5，则a 的值是（ ）A.－1或5B.1C.5D.－15.某种花卉每盆的盈利与每盆的株数有一定的关系，每盆植3株时，平均每株盈利4元；若每盆增加1株，平均每株盈利减少0.5元，要使每盆的盈利达到15元，每盆应多植多少株？设每盆多植x 株，则可以列出的方程是（ ）A .340.515x x +-=）（（）B .340.515x x ++=（）（）C .430.515x x +-=（）（）D . 140.515x x +-=（）（） 6.已知实数a ，b 分别满足2640a a -+=，2640b b -+=，则b aa b+的值是（ ） A.2 B.7 C.2或7 D.不确定 二、填空题:7.已知x 满足=+=+-xx x x 1,0152则 . 8. 已知关于x 的方程x 2+（1﹣m ）x +=0有两个不相等的实数根，则m 的最大整数值是 ．9.已知关于x 的一元二次方程230x x --=的两个实数根分别为α、β，则(3)(3)αβ++ = .10.若方程0962=+-x kx 有实数根，则K 满足的条件为 .11. 一个两位数等于它的个位数的平方，且个位数字比十位数字大3，则这个两位数为 . 三、解答题:12.选择适当方法解下列方程：（1）0152=+-x x ； （2）()()2232-=-x x x ；（3）x 2－5x －6=0； （4）x 2+2x －2=0（用配方法）13.已知关于的方程22(1)(1)0m x m x m --++=． （1）m 为何值时，此方程是一元一次方程？（2）m 为何值时，此方程是一元二次方程？并写出一元二次方程的二次项系数、一次项系数及常数项.14.已知关于x 的一元二次方程2(6)890a x x --+=有实根．（1）求a 的最大整数值；（2）当a 取最大整数值时，求出该方程的根．15.关于x 的方程04)2(2=+++k x k kx 有两个不相等的实数根.（1）求k 的取值范围.（2）是否存在实数k ，使方程的两个实数根的倒数和等于0?若存在，求出k 的值；若不存在，说明理由.16.某商场礼品柜台春节期间购进大量贺年卡，一种贺年卡平均每天可售出500张，每张盈利0.3元.为了尽快减少库存，商场决定采取适当的降价措施，调查发现，如果这种贺年卡的售价每降低0.1元，那么商场平均每天可多售出100张，商场要想平均每天盈利120元，每张贺年卡应降价多少元?寒假作业（1）答案一、选择题：1—6：A B B D A C二、填空题：7． 5 8. 0 9. 9 10. K ≤1 11. 25或26三、解答题：12.（1）152x =252x = (2) 122,3x x ==(3) 126,1x x ==-(4) 121,1x x ==13. （1）由题意得，⎩⎨⎧≠+=-,01,012m m 即当1m =时，方程22(1)(1)0m x m x m --++=是一元一次方程.（2）由题意得，210m -≠，即当1m ≠±时，方程22(1)(1)0m x m x m --++=是一元二次方程.此方程的二次项系数是21m -、一次项系数是(1)m -+、常数项是m .14. （1）根据题意得64469060a a ∆=-⨯-⨯≥-≠（）且， 解得709a ≤且a ≠6， ∴ a 的最大整数值为7.（2）当a=7时，原方程变形为2890x x -+=，644928∆=-⨯=，∴ x ，∴ 14x =24x =15. （1）由Δ=（k +2）2－4k ·4k ＞0，解得k ＞－1.又∵ k ≠0，∴ k 的取值范围是k ＞－1且k ≠0.（2）不存在符合条件的实数k . 理由如下：设方程2(2)04k kxk x +++=的两根分别为1x 、2x ， 由根与系数的关系有 122k x x k ++=-，1214x x ⋅=， 又01121=+x x ，则k k 2+-=0.∴ 2-=k . 由（1）知，2-=k 时，Δ＜0，原方程无实数解.∴ 不存在符合条件的实数k .16．设每张贺年卡应降价x 元， 则依题意得100(0.3)5001200.1x x ⎛⎫-+= ⎪⎝⎭， 整理，得21002030x x +-=，解得120.1,0.3x x ==-（不合题意，舍去）.∴0.1x =.答：每张贺年卡应降价0.1元。

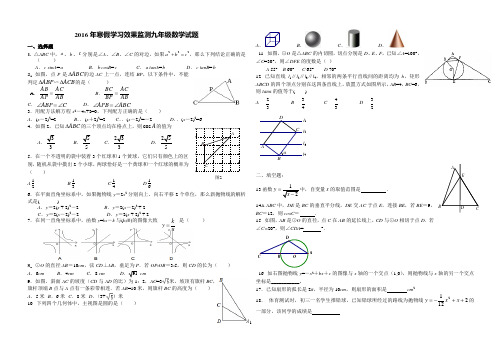
2016年寒假学习效果监测九年级数学试题一、选择题1. .△ABC 中，a 、b 、c 分别是∠A 、∠B 、∠C 的对边，如果222c b a =+，那么下列结论正确的是（ ） A ．c sinA =a B ．b cosB =c C ．a tanA =b D ．c tanB =b 2．如图，点P 是ABC ∆的边AC 上一点，连结BP ，以下条件中，不能判定ABP ∆∽ACB ∆的是（ ）A ．AB AC AP AB = B ．AB ACBP BC = C ．C ABP ∠=∠ D ．ABC APB ∠=∠3．用配方法解方程x 2－4x +2=0，下列配方正确的是（ ） A ．(x －2)2=2 B ．．(x ＋2)2=2 C ．．(x －2)2=－2 D ．．(x －2)2=6 4．如图2，已知ABC ∆的三个顶点均在格点上，则cos A 的值为ABCD5．在一个不透明的袋中装着3个红球和1个黄球，它们只有颜色上的区别，随机从袋中摸出2个小球，两球恰好是一个黄球和一个红球的概率为（ ）A .12B .13C .14D .166．在平面直角坐标系中，如果抛物线y ＝2x 2分别向上、向右平移2个单位，那么新抛物线的解析式是( )A ．y ＝2(x + 2)2－2B ．y ＝2(x －2)2 + 2C ．y ＝2(x －2)2－2D ．y ＝2(x + 2)2 + 2 7．在同一直角坐标系中，函数y =kx －k 与(k ≠0)的图像大致是（ ）8．⊙O 的直径AB ＝10cm ，弦CD ⊥AB ，垂足为P ．若OP :OB ＝3:5，则CD 的长为（ ） A ．6cm B ．4cm C ．8 cm D ．91 cm9．如图，斜面AC 的坡度（CD 与AD 的比）为1：2，AC =3米，坡顶有旗杆BC ，旗杆顶端B 点与A 点有一条彩带相连．若AB =10米，则旗杆BC 的高度为（ ） A ．5米 B ．6米 C ．8米 D ．（3+）米10. 下列四个几何体中，主视图是圆的是（ ）AB ．C ．D ．11. 如图，⊙O 是△ABC 的内切圆，切点分别是D 、E 、F ，已知∠A =100°，∠C =30°，则∠DFE 的度数是（ ）A .55°B .60°C .65°D .70°12. 已知直线l 1∥l 2∥l 3∥l 4，相邻的两条平行直线间的距离均为h ，矩形ABCD 的四个顶点分别在这四条直线上，放置方式如图所示，AB =4，BC =6，则tanα的值等于( ) A .23 B . 34 C . 43 D . 32二、填空题： 13.函数y =x 的取值范围是 ． 14△ABC 中，DE 是BC 的垂直平分线，DE 交AC 于点E ，连接BE ，若BE ＝9，BC ＝12，则cosC ＝ ． 15. 如图，AB 是⊙O 的直径，点C 在AB 的延长线上，CD 与⊙O 相切于点D ．若∠C=20°，则∠CDA = °．A16. 如右图抛物线y =－x 2＋bx ＋c 的图像与x 轴的一个交点（1,0），则抛物线与x 轴的另一个交点坐标是___________。

2016小学六年级寒假作业数学答案一、静心思考、填补空白(每空1分)18.8428.262.73282.733.253:213.06:23厘米秒克60至100都可以或1开放题二、明辨是非，正确判断(每空1分)√×√××三、去伪存真、慎重选择(每空1分)ACACB四、耐心细致、认真计算1.直接写出得数(每题0.5分)60211.3412.560.00890或142.求未知数解：2X=40…(2分)解：3X=5…(2分)解：x=×…(1分) X=20…(1分)X=…(1分)x=…(1分)X=…(1分)3.脱式计算1+0.54÷0.9-0.759×+9×+9×(÷)=1+0.6-0.75…(1分)=9×(++1)…(2分)=×(×)…(1分) =1.6-0.75…(1分)=18…(1分)=×…(1分)=0.85…(1分)=…(1分)(+-)×362-[+(-)]=×36+×36-×36(1分)=2-[+](1分)=16+30-14(1分)=2-(1分)=32(1分)=1(1分)五、手脑并用,实际操作1、作图题：2分画的三角形,底是4,高是6。

2、测量与计算：3分需要的材料:一根绳子一块石头一把米尺……(1分)用绳子一头绑上石头放入井中,沉入井底,再拎起绳子,量出绳子浸湿的长度即水的深度,再用米尺量出井口的直径,用3.14乘半径的平方再乘水深,就能测量出水的体积。

……(2分)以上就是为大家整理的六年级寒假作业数学答案，希望对大家有所启发!精心整理，仅供学习参考。

小学六年级数学寒假作业答案2016 第 9 页1) 1/20 1 1/4 7/3 2 3/7 12 1/6 9 52) (1) 8/9 9 1/9(2) 3/ 2 ÷3/8=4 3/2 ÷4=3/8(3) 4/3 1/12(4) > > 3) (1) × (2) × (3) × (4) √第 10 页4)(1) A (2) B (3) C (4) C5)(1) 7/9 ÷35/36=4/5(2) 4/5 ×3/4=3/5( 吨)(3) 8 ÷2/3 ×1/6=8 ×3/2 ×1/6=2(4) 180 ×1/3 ÷2/3=60 ×3/2=90第 11 页6) (1) 2+2=2 ×2 或0+0=0 ×0(2) ① 4/15 , 4/15 ② 9/70 , 9/70③ 25/66 , 25/66 ④ 36/91 , 36/91(3) 4 , 7 , 3/7 , 3/7 ,2/3 ×2/5 = 2/3 - 2/5( 此小题答案多种)7)(1) 21 ÷ 7/17 =51( 枚)(2) 8 ÷(1-3/4)=8 ×4=32( 千克)(3) 750 ÷(1-7/32)=750 ÷32/25=960( 米)第12 页(4) 96-45=51( 页)明明: 96 ×3/4-15=72-15=72-15=57( 页) ≠51( 页)聪聪: 96 ×1/2+3=48+3=51( 页)=51( 页)答: 聪聪说得对.提高篇:(1) 原式=2010/2011 ×(2011+1)=2010+2010/2011=2010 又2010/2011( 对不起, 打出的分数在博文中显现不出来, 只能这样打了)(2) 原式=63/2 ×2/3+124/3 ×3/4+205/4 ×4/5=21+31+41=93(3) 原式=3/2 ×4/3 ×5/4 ×…… ×100/99 ×101/100=101/2第13 页1)10 1/2 1 16/25 6/5 5/16 1/12 1/22)(1) 5:6 6:5 (2) 4:5 4:9 (3) 15 12 30/503) 2:3 2/3 2:1 2 5:1 5 5:2 5/24)(1) ×第14 页(2 )×(3 )√(4 )×5 )(1 )X=5/21 X=2/11 X=3/26 ) 4/5 ， 53 ， 7/6 ， 18/77 )( 1 ) 12 0 ÷5/6=144 (吨)第15 页(2 )(42-24 )÷1/4=18 ×4=72(3 )18 ÷3/5-18=30-18=12 (人)(4 )(2/5 ÷4) ×(2/5 ÷4)=1/10 ×1/10=1/100( 平方米)8 )(1 )5.4 ÷(1+8 )=5.4 ÷9=0.6 (千克)0.6 ×8=4.8 (千克)(2 )360 ×(1-1/3 )=240 (只) 5+3=8 (份)黑兔：240 ×5/8=150 (只)灰兔：240 ×3/8=90 (只)白兔：360 ×1/3=120 (只)第16 页( 3 ) 9 ， 36 ， 12提高篇1 )( 1 ) 7 ： 9 (2 ) 2 ：3 ： 5 ( 3 ) 3 ：4 ： 102 )梨的质量是橘子的 2/5 ，说明梨和橘子质量的比是 2 ： 5则梨、橘子和苹果质量的比是 2 ： 5 ： 6 ，即三种水果共分成 2+5+6=13 (份)梨占 2/13 ，所以梨有260 ×2/13=40 (千克) 第 17 页1) 1/5 1 1/25 2 6/51/4 28/45 9 又 3/52)(1) C (2) B (3) B (4) A3) (1) 15 24 0.375(2) 10:1 , 10(3) 40 , 50(4 ) 8 又 1/3第 18 页(5) 3:4(6) 1/5 1/4(7) 7/64) 80+60+100=240( 千瓦时 )小明家: 12 0 ×80/240=40( 元) 小红家:120 ×60/240=30( 元)小华家:120 ×100/240=50( 元)5) X=5/2 X=1/186) 答: 这个比与教科书中的比不同. 体育比赛中只是记载得分情况.第19 页7) (1) 1+2+3=6( 份 )低年级:36 0 ×1/6=60( 本)中年级:360 ×2/6=120( 本)高年级:360 ×3/6=180( 本)(2) 2+3=5 (份) 3/ 5 ×2/5=6/25 (千克)( 3 )① 0. 5 ×1000=500 (千克)② 1000+1=1001 药液：160.16 ×1/1001=0.16 (千克)(4 )5+3=8 (份) 白昼：24 ×5/8=15 (小时) 24 ×3/8=9 (小时)第20 页(5 ) 350 ×(1-1/7 )=350 ×6/7=300 (千米/ 时)(6 )解：设这条水渠全长X 千米。