哈尔滨工程大学试卷11

哈尔滨工程大学考研真题一、简要说明下列各种力产生的原因、求解思路及表达式1、 沿程阻力2、形状阻力3、惯性阻力4、机翼升力5、湍流应力二、图示水箱1中的水经光滑无阻力的圆孔口水平射出，冲到一平板上。

平板封盖着另一水箱2的孔口，水箱1中水位高度为1h ，水箱2 的水位高度为2h ，两孔口中心重合，而且直径12d d /2=。

若射流的形状时对称的，冲击到平板后转向平行于平板的方向，并向四周均匀流出。

假定流动是无粘性不可压缩定常的，平板和水质量力不计。

当已知1h 和水的密度ρ时，求保持平板封盖住水箱2的孔口时2h 的最大值。

三、工程中常用文丘里管测量管路中水的流量。

管路和收缩管段截面积分别为1S 、2S ，水的密度和U 型测压计中液体的密度分别为ρ、m ρ，且m ρρ〈。

若不计水的粘性，试导出倾斜管路中水的流量Q 与测压计中液体的高度差读数h 之间的关系式。

四、设在平面直角域中点A （a ，b ）处放着一个强度为Q 的平面点源，0,0x y ==是半无限固体壁面，远方压力为ρ∞。

试求： 1. 平面流动复势W(z)； 2. 壁面上流体的速度分布；3. 壁面0x =上流体的压力分布。

五、两块无限长二维平行平板如图所示，其间充满两种密度和粘性系数分别为12,ρρ和12,μμ的液体，高度分别为1h ，2h 。

已知下板静止，上板以速度U 向右运动，全流场应力相同，不计重力，流体运动为层流。

试求流场中的速度分布。

六、圆球在静水中释放后上浮，圆球的半径为a ，水和圆球的密度分别为,w m ρρ。

忽略水的粘性，试求圆球上浮运动之距离随时间的变化规律。

标准答案 一、（分析）考察学生对流体力学中出现的专业中常用的有关力的掌握程度。

1、沿程阻力：管道壁面粘性摩擦和粗糙度引起的阻力。

表达为圆管沿程阻力系数，2f l Vh d gλ∆= 2、形状阻力：由于粘性和流动分离产生的压力沿流动方向投影的合力。

求得压力后积分或试验测得，20cos 12p n D sD D p ds C U A αρ==⎰⎰或3、惯性阻力：非定常运动改变流体的惯性引起的阻力。

考研哈工大试题及答案一、选择题（每题2分，共10分）1. 下列哪个选项是哈尔滨工业大学的简称？A. 哈工大B. 哈师大C. 哈理工D. 哈工程答案：A2. 哈尔滨工业大学位于哪个省份？A. 黑龙江省B. 吉林省C. 辽宁省D. 内蒙古自治区答案：A3. 考研初试中，数学科目满分为多少分？A. 100分B. 150分C. 200分D. 300分答案：B4. 下列哪一项不是考研复试的内容？A. 笔试B. 面试C. 体检D. 体育测试答案：D5. 考研复试通常在初试成绩公布后的多长时间内进行？A. 1个月B. 2个月C. 3个月D. 4个月答案：B二、填空题（每题2分，共10分）1. 考研初试成绩一般由________和________两部分组成。

答案：公共课、专业课2. 考研复试时，考生需要携带的材料包括________、________和准考证等。

答案：身份证、学生证3. 考研复试中，面试环节主要考察考生的________能力和________能力。

答案：专业、沟通4. 考研初试中，英语科目的考试时间为________分钟。

答案：1805. 考研初试成绩公布后，考生可以通过________和________查询成绩。

答案：研招网、学校官网三、简答题（每题10分，共20分）1. 简述考研复试的重要性。

答案：考研复试是选拔研究生的重要环节，它不仅考察考生的专业知识和技能，还考察考生的综合素质和学术潜力。

复试成绩在最终录取中占有重要比重，因此考生需要认真准备，充分展示自己的实力。

2. 描述考研初试和复试的区别。

答案：考研初试主要考察考生的公共课和专业课知识，通常以笔试形式进行。

复试则更注重考生的综合素质和专业能力，包括面试、笔试和体检等环节。

初试成绩是进入复试的门槛，而复试成绩则直接影响最终的录取结果。

四、论述题（每题20分，共40分）1. 论述如何有效准备考研复试。

答案：有效准备考研复试的方法包括：一是提前了解复试流程和要求，二是复习专业知识和技能，三是加强沟通和表达能力训练，四是进行模拟面试练习，五是保持良好的心态和身体状况。

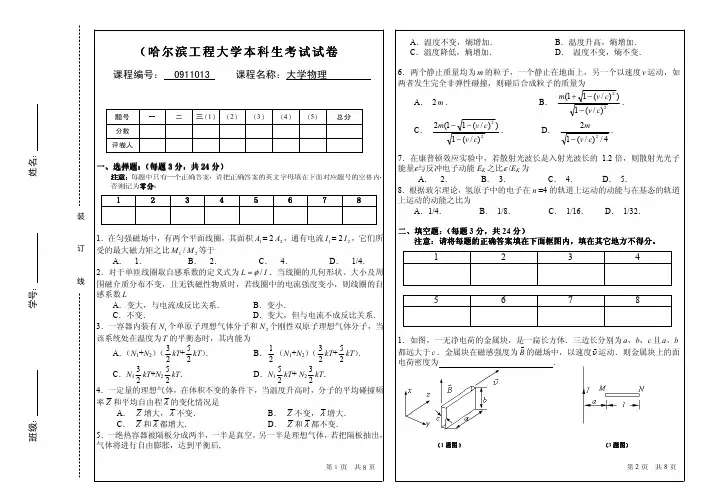
（哈尔滨工程大学本科生考试试卷A．温度不变，熵增加． C．温度降低，熵增加．B．温度升高，熵增加． D． 温度不变，熵不变．课程编号： 0911013 课程名称：大学物理6．两个静止质量均为 m 的粒子，一个静止在地面上，另一个以速度 v 运动，如两者发生完全非弹性碰撞，则碰后合成粒子的质量为m(1 + 1 − (v / c)2 )A． 2 m ．B．．题号 一 二 三（1） （2） （3） （4） （5） 总分1 − (v / c)2分数2m(1 − 1 − (v / c)2 )C．．D．2m ．评卷人1 − (v / c)21 − (v / c)2 / 4：7．在康普顿效应实验中，若散射光波长是入射光波长的 1.2 倍，则散射光光子一、否注选则意择记：题每为：题零（中分每只。

题有一3 个分正，确共答2案4，分请）把正确答案的英文字母填在下面对应题号的空格内，能量ε与反冲电子动能 EK 之比ε /EK 为A． 2．B． 3．C． 4．D． 5．8．根据玻尔理论，氢原子中的电子在 n =4 的轨道上运动的动能与在基态的轨道12345678上运动的动能之比为A．1/4．B． 1/8．C． 1/16． D． 1/32．姓名装学号订1．在匀强磁场中，有两个平面线圈，其面积 A1 = 2 A2 ，通有电流 I1 = 2 I 2 ，它们所受的最大磁力矩之比 M1 / M 2 等于A． 1．B． 2．C． 4．D． 1/4．二、填空题：（每题 3 分，共 24 分）注意：请将每题的正确答案填在下面框图内，填在其它地方不得分。

12342．对于单匝线圈取自感系数的定义式为 L = φ / I ．当线圈的几何形状、大小及周线：围磁介质分布不变，且无铁磁性物质时，若线圈中的电流强度变小，则线圈的自感系数 L A．变大，与电流成反比关系．B．变小．5678C．不变．D．变大，但与电流不成反比关系．3．一容器内装有 N1 个单原子理想气体分子和 N 2 个刚性双原子理想气体分子，当该系统处在温度为T 的平衡态时，其内能为A．（N1+N2）（3 2kT+5 2kT）．B．1 2（N1+N2）（3 2kT+5 2kT）．C．N13 2kT+N25 2kT．D．N15 2kT+N23 2kT．、 、 、 1．如图，一无净电荷的金属块，是v一扁长方体．三边长v分别为 a b c 且 a b都远大于 c ．金属块在磁感强度为 B 的磁场中，以速度v 运动．则金属块上的面电荷密度为．4．一定量的理想气体，在体积不变的条件下，当温度升高时，分子的平均碰撞频率 Z 和平均自由程 λ 的变化情况是：A． Z 增大， λ 不变． C． Z 和 λ 都增大．B． Z 不变， λ 增大． D． Z 和 λ 都不变．5．一绝热容器被隔板分成两半，一半是真空，另一半是理想气体，若把隔板抽出， 气体将进行自由膨胀，达到平衡后,（1 题图）（3 题图）第1页 共8页第2页 共8页班级2．一平行板空气电容器的两极板都是半径为 R 的圆形导体片，在充电时，板间（本题 分） 三、计算题：（共 52 分）1、 10 如图所示，一半径为 R 的均匀带电无限长直圆筒，面电荷密度为电场强度的变化率为 dE / dt ．若略去边缘效应，则两板间的位移电流为． σ ．该筒以角速度ω 绕其轴线匀速旋转．试求：圆筒内部的磁感强度．3．如图所示，一段长度为 l 的直导线 MN，水平放置在载电流为 I 的竖直长导线 旁与竖直导线共面，并从静止由图示位置自由下落，则 t 秒末导线两端的电势差 U M − U N = ______________________．4．如图 3 所示的曲线分别表示了氢气和氦气在同一温度下的分子速率的分布情 况．由图可知，氢气分子的最概然速率为______________________．（ 的 ． 的 ． ） H2 M mol = 2 ×10−3 kg mol-1; He M mol = 4 ×10−3 kg mol-1装订线（4 题图）（8 题图）5．一定量的理想气体在 p − V 图中的等温线与绝热线交点处两线的斜率之比为 0.714，则其定体摩尔热容为．6．设以氮气(视为刚性分子理想气体)为工作物质进行卡诺循环，在绝热膨胀过程中气体的体积增大到原来的两倍，则该循环的效率为．7．假如电子运动速度与光速可以比拟，则当电子的动能等于它静止能量的 2 倍时，普朗克常量 ，电子静止质量 其德布罗意波长为 (．h =6.63×10-34 J·sme=9.11×10-31 kg)8．一粒子被限制在相距为 l 的两个不可穿透的壁之间，如图所示．描写粒子状态 的波函数为ψ = cx(l − x) ，其中 c 为待定常量．求在 0~ 1 l 区间发现该粒子的概3率．．第3页 共8页第4页 共 8页（本题 分） 2、10 一半径为 R 的无限长半圆柱面型导体，与轴线上的长直导线载有等值相反的电流 I，如图所示.求：半无限长圆柱面电流单位长度上所受的力.（本题 分） 3、 10 无限长直导线旁有一与其共面的矩形线圈，直导线中通有v 恒定电流 I，将此直导线及线圈共同置于随时间变化的而空间分布均匀的磁场 B 中．设∂B>0v ，当线圈以速度 v垂直长直导线向右运动时，求线圈在如图所示位置时的∂t感应电动势．：姓名装订线：学号班级：第5页 共8页第6页 共8页（本题 分） 4、 10 1 mol 双原子分子理想气体作如图的可逆循环过程，其中 1－2 为直线，2－3 为绝热线，3－1 为等温线．已知T2 = 2T1 ，V3 = 8V1 ，θ = 450 。

为两个随机事件，则下列选项中正确的是 。

(A) ()A B B A -=U (B) ()A B B B -=U (C) ()A B B A -⊂⎡⎤⎣⎦U(D) ()A B B A -⊃⎡⎤⎣⎦U2. 设随机变量X 服从参数为(0)λλ>的泊松分布，且{1}{2}P X P X ===，则(1)D X +的值为 。

(A) 2(B) 3(C) 14(D) 543. 设随机变量X 与Y 相互独立且都服从参数为(0)λλ>的指数分布，则),min(Y X 服从 。

(A) 参数为λ的指数分布 (B) 参数为λ2的指数分布 (C) 参数为2λ的指数分布 (D) ),0(λ上的均匀分布4. 设n X X X ,,,21Λ是来自正态总体),(2σμN 的简单随机样本，X 表示样本均值，2S 表示样本方差，则下列选项中错误的是 。

(A))1,0(~N nX σμ-(B))(~n t nSX μ-(C))1(~)1(222--n S n χσ(D) X 与2S 相互独立5. 设n X X X ,,,21Λ是来自正态总体),(2σμN 的简单随机样本，若进行假设检验，当 时，一般采用统计量nSX T 0μ-=。

(A) μ已知，检验220σσ=(B) μ未知，检验220σσ=(C) 2σ已知，检验0μμ=(D) 2σ未知，检验0μμ=1. 某人向同一目标独立重复进行射击，每次射击命中的概率为)10(<<p p ，则此人第4次射击恰好是第2次命中目标的概率为 。

2. 在[0,1]中随机取数x ，在[1,2]中随机取数y ，则事件32x y ⎧⎫+≥⎨⎬⎩⎭的概率为 。

3. 设随机变量X 与Y 相互独立且服从同一分布：1{}{}3k P X k P Y k +====(0,1)k =，则概率{}P X Y =的值为 。

4. 设随机变量X 的数学期望为μ，方差为2σ，则由契比雪夫不等式可知概率{}3P X μσ-≥≤ 。

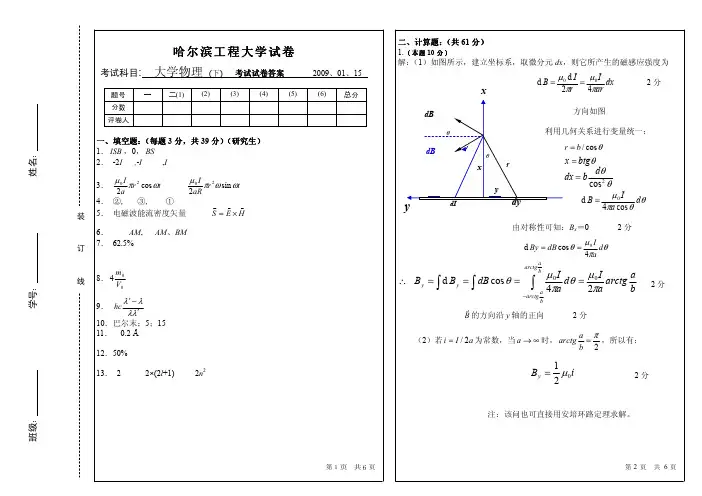
班级：学号：第1页 共2页第2页 共2页所有试题答案均需写在答题册上，写在本试卷上无效。

一、简答题（每空1分，共60分）1.组合声纳参数中噪声隐蔽级的表达式为 ；混响隐蔽级的表达式为；它们都表示主动声纳正常工作所需的最低 。

2.主动声纳的背景干扰有 和 。

其中 是平稳的随机过程，是非平稳的随机过程。

对应两种不同干扰背景的主动声纳方程分别为和 。

3.在水声学中，声压级的定义式为 ；声强级的定义式为 ；声压级与声强级相等的条件为 。

4.已知发射换能器的辐射声功率为100W ，则距离声源声中心1m 处无指向性声源的声强为 W /㎡；声源级为 dB 。

5.传播损失的一般表示式为 。

其中几何衰减项为 、物理衰减项为 。

6.影响海水声速的三个主要因素为 、 、 。

海水中声速的典型结构有 、 、 、 。

7.一般情况下，声波的频率越低，海水的吸收衰减 ，传播距离 ；但当声波的频率低于波导的 频率时，简正波水平方向的波数由实数变为 ，波导中的简正波蜕化为 的简正波，传播距离反而 。

8.射线声学的两个基本方程分别为 方程和 方程。

由Snell 折射定律可知，声线总是向 的方向弯曲；当介质的声速为常数时，声线轨迹为 ；当介质的声速梯度为常数时，声线轨迹为 ，圆的半径为 。

9.声波在 声道和 声道中能够远距离传播。

10.邻近海面水下点源声场声压振幅随距离的变化关系表现为：近场菲涅耳干涉区，声压振幅随距离 减小，远场夫琅和费区，声压振幅随距离 减小。

11.水池中测量目标强度，一般可采用比较法或直接测量法，但应注意：第一，声源与目标之间的距离和目标与水听器之间的距离都应满足 条件。

第二，应保证 条件得到满足。

第三，合理选取发射信号 。

12.目标回声信号的形成主要有 、 、 、 。

回声信号的一般特征为 、 、、 。

13.根据混响形成原因的不同，习惯上将海洋混响分为 、 和 ；其中和 又统称为界面混响。

混响的瞬时值服从 分布；振幅服从 分布。

A. 微分分布B. 能量注量C. 能量注量率D.积分分布 3、能注量率的量纲是（ D ）A. Cm 2kg -1B. Jm 2Kg -1C. Jm -2 s -1D.Jm -2s 1 4、单位径迹长度上产生离子对数称为（ C ）。

A. 质量减弱系数B. 能量损失率C. 比离电离D. 碰撞阻止本领 5、当量剂量的单位是（ B ）A. 戈瑞（Gray ）B. 希沃特（Sv ）C. 贝可（Bq ）D. 库仑（C ） 6、在内照射的剂量系数是指在年龄为t 0时的每单位摄入的( A )大小。

A 、待积有效剂量 B 、待积吸收剂量 C 、待积比有效能量 D 、待积年摄入量7、低Z 介质在前，高Z 介质在后，则总积累因子值（ A ）A. ］高)(,[d E B μγB. ］低)(,[d E B μγC. ］］低高)(,[)(,[d E B d E B μμγγ•D. ］高低)(,)[(min ,d E B μγ四、多选题（每题1分，共5分） 1、属于随机性效应有( AC )。

A 、癌症B 、不育C 、白血病D 、β射线的皮肤烧伤 2、下列的国际单位是J ٠kg 可能剂量学量有( ABD )。

A 、吸收剂量B 、当量剂量C 、照射量D 、有效剂量3、电子的电离能量损失和辐射能量损失之比与( AD )因素相关。

A 、带电粒子的能量 B 、带电粒子的原子序数 C 、带电粒子的质量 D 、吸收物质的原子序数4、人类引起活动天然照射的升高因素有( ABCD )。

A 、煤开采B 、有色金属工业C 、石油工业D 、民航工业 5、人的外照射急性放射病可分为( ABC )。

A 、骨髓型急性放射病 B 、肠型急性放射病 C 、脑型急性放射病 D 、血液型急性放射病五、问答题（每题10分，共20分）1、β粒子外照射防护有哪些特点，对β源的屏蔽设计有哪些考虑因素？2、核电厂的辐射源项有哪些？六、计算题（每题10分，共20分）。

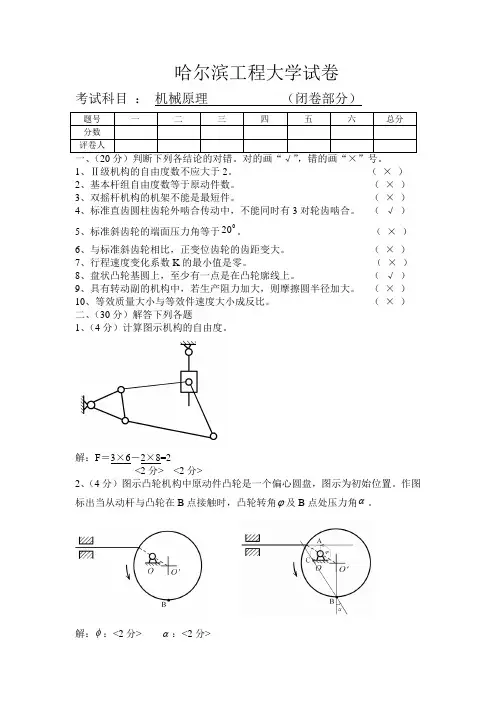
哈尔考试科目：机械原理（闭卷部分）1、Ⅱ级机构的自由度数不应大于2。

（×）2、基本杆组自由度数等于原动件数。

（×）3、双摇杆机构的机架不能是最短件。

（×）4、标准直齿圆柱齿轮外啮合传动中，不能同时有3对轮齿啮合。

（√）20。

（×）5、标准斜齿轮的端面压力角等于06、与标准斜齿轮相比，正变位齿轮的齿距变大。

（×）7、行程速度变化系数K的最小值是零。

（×）8、盘状凸轮基圆上，至少有一点是在凸轮廓线上。

（√）9、具有转动副的机构中，若生产阻力加大，则摩擦圆半径加大。

（×）10、等效质量大小与等效件速度大小成反比。

（×）二、（30分）解答下列各题1、（4分）计算图示机构的自由度。

解：F＝3×6－2×8=2<2分> <2分>2、（4分）图示凸轮机构中原动件凸轮是一个偏心圆盘，图示为初始位置。

作图标出当从动杆与凸轮在B点接触时，凸轮转角ϕ及B点处压力角α。

解：φ：<2分> α：<2分>3、（9分）图示斜面中，滑块受铅垂向下力Q 及与斜面平行力F 。

斜面倾角为λ，滑块与斜面间摩擦系数f 及Q 已确定。

求滑块匀速上升及匀速下降时，该斜面效率表达式各是什么？解：F=Qsin λ+ f Q λ F 0= Qsin λ <3分>η = sin λ/（ sin λ+ f c λ） <3分> η= （sin λ－fco λ）/sin λ <3分> ＜3×3=9分＞ 4、（4分）图示铰链四杆机构中，所标数字代表杆长，单位为cm 。

若使该机构为双曲柄机构，试确定AD 杆长的取值范围。

解：0﹤ AD ≦20 <4分>5、（9分）国产正常齿标准直齿圆柱齿轮外啮合，已知：mm d 35.1501b =，mm d a 2562=，5.1i 12=，又知1*=a h ，25.0*=c ，α=20°，求：1d 、m 、和b1p解：d 1= d b /cos α=160mm <3分> 依ｄa1 =i 12 d 1+２h *m 得m=8mm <3分>p b =πmcos α=23．62 mm <3分> ＜3×3=9分＞哈尔滨工程大学试卷考试科目 ： 机械原理 （开卷部分）三、（16分）图示轴类转子中，知两端面A 及B 上分别有不平衡质量A m 、B m ，方位如图。

2011年春季学期《传热学》（A 卷）答案一．（10分）外直径为50mm 的蒸汽管道外表面温度为400℃，其外包裹有厚度为40mm 、导热系数为0.11W/(m·K)的矿渣棉。

矿渣棉外又包有厚为45mm 的煤灰泡沫砖，导热系数为0.12W/(m·K)，煤灰泡沫砖外表面温度为50℃，试求通过每米长该保温层的热损失，并给出矿渣棉外表面温度。

解：由多层圆筒壁的导热热流量公式可知：()()()132113222ln ln l t t d d d d πλλ-Φ=+（3分）其中4001=t ℃,503=t ℃,1=l m,12350,130,220d mm d mm d mm === （2分）=1λ0.11W/(m·K),=2λ 0.12W/(m·K) 带入公式，可得：25.168=ΦW （1分）设矿渣棉外表面温度为2t ，则由能量守恒定律可知：()()122112ln l t t d d πλ-Φ=（3分），代入数据，可得：39.1672=t ℃（1分） 二．（10分）直径为12mm 、初始温度为1150K 的钢球，突然被放置于温度为325K 、表面传热系数为20W/(m 2·K)的空气中冷却。

已知钢球的物性如下：λ=40W/(m·K)，ρ=7800kg/m 3，c=600J/(kg·K)。

试确定钢球中心温度被冷却到400K 所需的时间？如果考虑辐射的影响，冷却时间应延长还是缩短？解：这是一个典型的非稳态热传导问题，先计算其毕渥数的大小：1.0001.0403006.020)/<=⨯==λA V h Bi （，故可以利用集总参数法计算此非稳态问题。

（2分） 由公式：⎪⎪⎭⎫ ⎝⎛-=--=∞∞τρθθcV hA t t t t exp 00 （4分） 可得：⎪⎪⎭⎫⎝⎛---=∞∞t t t t hA cV0ln ρτ（1分） 代入数值，可得：21.1122=τs （1分）如果考虑辐射的影响，则钢球的散热强度增强，冷却时间会缩短。

1. 已知1e ,0,()1sin ,0.xx a x f x x x x -⎧-≤⎪=⎨⎪>⎩为连续函数，则a = .2. 已知函数2xy x =，则微分1d |x y == d x .3. 函数x y xe =的n 阶麦克劳林公式中，含nx 项的系数是 . 4. 已知定积分220111()cos ()d 0x c x c x ++=⎰，则常数c = .5. 心形线1cos (02)r θθπ=+≤≤的全长为 .1. 当0x +→时，与等价的无穷小量是（ ）. (A) 1-(B )(ln 1+ (C ) 1-(D ) 12. 设函数e ()()(1)x bf x x a x -=--有无穷间断点0x =、可去间断点1x =，则常数,a b 的值为 （ ）.(A ) 0a =，1b = (B ) 0a =，e b = (C ) a 任意，1b =(D ) a 任意，e b =3. 设()33f x x x q =-+，其中常数()2,2q ∈-，则()f x 的零点的个数为 （ ）.(A ) 1(B ) 2 (C ) 3 (D ) 44. 下列广义积分收敛的是（ ）.(A )1x +∞⎰(B )0d xxex --∞⎰(C )1311d x x-⎰(D )1+∞⎰哈尔滨工程大学本科生考试试卷（ 2010 年 秋季 学期）5. 下列说法正确的是 （ ）.(A ) 已知数列{}n x 单调递增，非负函数()f x 单调递减，则数列{()}n f x 收敛 (B ) 设函数()f x 连续，且满足()m f x M ≤≤，其中,m M 为常数，则()()d ()b am b a f x x M b a -≤≤-⎰(C ) 11(1)d (1)1x x x e e x e C ααα++=+++⎰ (D ) 设函数()f x 连续，若00(,())x f x 是曲线()y f x =的拐点，则0()f x不是()f x 的极值1. 计算极限210tan lim x x x x +→⎛⎫ ⎪⎝⎭.2. 已知函数()y y x =是由方程arctan x y=d d y x ，22d d y x .3. 已知函数()y y x =由参数方程2221212201e e d (1)e d t y t u u x t u u u ⎧=⎪⎨⎪=+⎩⎰⎰确定，求d d y x ，22d d yx .4. 设()22e d x t x t -Φ=⎰，求（1）()y x =Φ的单调区间； （2）()y x =Φ的凹凸区间.1. 计算积分x ⎰.2. 计算积分241xx⎰.3. 设()f x ''在[0,1]连续，且(0)1,(2)3,f f ==(2)5,f '=计算积分10(2)d .x f x x ''⎰已知抛物线22y x =-、直线y x =以及y 轴在第一象限围成了平面图形D ，求（1）D 的面积； （2）D 绕y 轴旋转一周所得的旋转体的体积.1. 当0x >时，证明不等式：2cos xe x x ->-.2. 已知函数()f x 在[]0,1上有二阶导数，10()d 0f x x =⎰，(0)(1)0f f ==.（1）证明：存在(0,1)ξ∈，使得()0f ξ=； （2）证明：存在(0,1)η∈，使得22()()1f f ηηηη'''=+.3. 利用N ε-语言，证明极限2233lim212n n n n →∞+=-.微积分A(一)2010级期末试题（A 卷） 参考答案及评分标准(2011年1月11日)一、填空题（每小题3分，共15分）1. 12. 23.1(1)!n - 4. 32- 5. 8二、单项选择题（每小题3分，共15分）1. B2. B3. C4. D5. A三、计算题（每小题8分，共32分）1. 解答：1tan tan 00tan tan lim()lim(1)xx x x x x x x x x x x x x++-⋅-→→-=+ ……2分而22322000tan sec 1tan 1lim lim lim 333x x x x x x x x x x +++→→→--=== 所以21130tan lim()x x x e x+→= ……6分2. 解答：方程两边同时对x 求导：2222y xy x yy x y x y''-+=++ 故dy y x dx x y -=+ ，即 12dy xdx x y=-+ ……4分 ()222223(1)2()2()d y x y x y x y dx x y x y '+-+-+=-=++ ……4分3. 解答：221221e d (1)ed y tu u u u u =+⎰⎰两边对t 求导：2222(1)t y t e y t e '=+，故2222(1)t y t y e t e -'=+ ……3分 22222222d (1)d (1)t y y t t t y ye t e e x x t e --'+==='+； ……3分 222222d ()(2)2d y y y y de dy e y ye x dx dx---==-=-。

(,,)A x y z =连续偏导数，则下列运算没有意义的是rot(rot )A )A grad(div )Agrad(rot )A分方程xy y '''+=其对应的的一个特解为ln x ，则的通解为 。

22ln x C x ++2ln x C x x ++e x x C x ++e x x C -++)(1)n a+3. 将函数21()23f x x x =--展开成x 的幂级数，并指出收敛域。

4. 设函数)(x f 以π2为周期,其在),[ππ-上的表达式为x x f 2)(=,试将)(x f 展开成周期为π2的傅里叶级数。

微积分A （二）A 卷期末考试答案及评分标准（2011年7月15日）一、填空题（每小题3分，共15分） 1. 11d d x y x y +；2. 12-；3. 12x y +；4. π；5. 222e 2y x C y =--。

二、单项选择题（每小题3分，共15分）1. B ；2. D ；3. C ；4. D ；5. A 。

三、计算题I （每小题7分，共28分）1. 解答：12zf yf x ∂''=+∂21112222()zf x y f xyf f x y∂'''''''=++++∂∂2. 解答：12121(1)(1)(1)lim lim (1)(1)(1)n nn n n n n nu a a a a u a a a a +++→∞→∞+++=⋅+++1lim 1n n aa +→∞=+ 1a <时，1lim 1n n nua u +→∞=<1a >时，1lim 01n n nuu +→∞=<1a =时，11lim 12n n nu u +→∞=<综上，对任何0a >，级数都是收敛的。

3. 解答：()d M x y z v Ω=++⎰⎰⎰111L L L +-⎰⎰[(e cos 1)xDy -⎰⎰20d d 2RDx y x +⎰⎰⎰2(4)2R π+ 22,0y R z +≤=31)d d (1)d y z y ∑++''∑+∑∑-⎰⎰⎰⎰223(x y z Ω++⎰⎰⎰2/23d sin ππθ⎰⎰5265R R ππ=+。

第2页 共 2页Figure 1 Figure 22. (12 points)series coefficients:X [k ] = -j δ[k - 2] + j δ[k +2] + 2δ[k - 3] + 2δ[k + 3], ω0 = π(2) Determine the discrete-time Fourier series (DTFS) coefficients of the periodic signals depicted in Fig.3.Figure 3 Figure 46. (10 points)Determine and draw sketches of the Fourier series and Fourier transform representation of the square wave depicted in Fig.47. (8 points)(1) Compute the discrete-time Fourier transform (DTFT) of the signal depicted in Fig.5.Figure 5 Figure 6(2) Draw the Fourier transform of a impulse-train sampled version of the continuous-time signal having the Fourier transform depicted in Fig.6 for (a) T = 1/2(s) and (b) T = 2(s), where T is sampling period.8. (6 points)Shown in Fig.7 is the frequency response H (j ω) of a continuous-time filter. For each of the input signals x (t ) below, determine the filtered output signal y (t ).(1) x (t ) = cos(2πt +θ) (2) x (t ) = cos(4πt +θ)第3页 共4页 第4页 共 4页Figure 79. (8 points)Find the inverse Fourier transform of the following spectra: (1) X (j ω) = 2δ(ω - 4) (2) X (e j ω) = 2cos(2ω)(3) X (j ω) = ⎩⎨⎧><πωπωω,0,cos 2(4) X (e j ω) = ⎩⎨⎧<<-otherw ise02 4,/,πωπωj e , on -π < ω < π10. (16 points)Consider a continuous-time LTI system for which the input x (t ) and output y (t ) are related by the differential equationy" (t ) - y' (t ) - 6y (t ) = x' (t ) + x (t )(1) Determine the frequency response H (j ω) of the system.(2) Determine the system function H (s) of the system. Sketch the pole-zero plot of H (s )(3) Determine the system impulse response h (t ) for each of the following cases:(a) The system is stable; (b) The system is causal.(4) Let x (t ) = e -2t u (t ). Find the output y (t ) of the causal system.11. (6 points)Consider a message signal m (t ) with the spectrum shown in Fig.8. The message bandwith ωm = 2π×103 rad/s. The signal is applied to a product modulator, together with a carrier wave A c cos(ωc t ), producing the modulated signal s (t ). The modulated signal is next applied to a synchronous demodulator (shown in Fig.9).(1) Determine the spectrum of the demodulator output when (a) the carrier frequency ωc = 2.5π×103 rad/s and (b) the carrier frequency ωc = 1.5π×103 rad/s.(2) What is the lowest carrier frequency for which each component of the modulated signal s (t ) is uniquely determined by m (t ).Figure 8 Figure 912. (6 points)(1) Draw a sketch of the spectrum ofx (t ) = cos(50πt )sin(700πt )Label the frequencies and complex amplitudes of each component.(2) Determine the minimum sampling frequency that can be used to sample x (t ) without aliasing for any of the components.。

2011-01-041、（）.Ａ．Ｂ．Ｃ．Ｄ．不存在2、若在发散，则它在（）.A. 收敛Ｂ．收敛 C. 发散 D. 均不正确3、已知函数，则，分别是的（）.Ａ．二阶极点、孤立奇点Ｂ．二阶极点、非孤立奇点Ｃ．可去奇点、孤立奇点Ｄ．可去奇点、非孤立奇点4、映射在处的旋转角为（）.Ａ．Ｂ． C. D.5、下列命题或论断中，正确的个数是（）.I：Ⅱ：设解读，则是的共轭调和函数III：的导数存在的充要条件是的偏导数分别存在Ⅳ：在任意圆环域不能展开为洛朗级数Ａ．Ｂ．Ｃ．Ｄ．36、设，则 .7、若函数为某一解读函数的虚部，则常数 .8、设函数的泰勒展开式为，则它的收敛半径为 .9、设信号，则通过Fourier变换得到的频谱函数 .10、设，则通过Laplace逆变换得到 .11、函数在何处可导？何处解读？12、设是解读函数，且，求.13、计算积分，其中为负向，为整数.14、计算积分，其中为正向.15、利用留数定理计算定积分.16、求函数在下列要求下的级数(泰勒或者洛朗级数)展开：(1) 圆内；(2) 环内；(3) 环内.17、设正向，试求：(1) 在复平面上除去的点处的函数表达式；(2) 及.18、按照要求逐步完成下列有关保形映射的问题.(1) Z平面阴影部分是角形区域，如下图所示。

通过何种变换，保形映射为.(2) ，在下图中画出经过该映射后的区域.19、质量为的物体挂在弹簧系数为的弹簧一端（如下图所示），其中常数为固有频率，为作用在物体上的外力。

若物体从静止平衡位置开始运动，物体的初始位移初始速度大小，根据牛顿定律可得到方程：假设在初始时刻时，物体受到外力（为单位冲击函数），应用Laplace变换，求解物体的运动规律。

x20、假设在给定区域D解读，且，若为常数，证明：为常数.21、若收敛而级数发散，证明：幂级数的收敛半径为1.。