一阶数字低通滤波器
- 格式:doc
- 大小:20.50 KB
- 文档页数:1

一阶滤波算法在信号处理中,滤波是一种常用的技术,它可以通过去除或者削弱一些不需要的信号成分,从而使得信号更加清晰、稳定。
一阶滤波算法是滤波中的一种基础算法,它可以被广泛应用于各种领域,例如声音处理、图像处理、控制系统等等。
本文将介绍一阶滤波算法的原理、应用以及优缺点。
一、一阶滤波算法的原理一阶滤波算法的原理很简单,它是一种线性滤波算法,可以用一个一阶差分方程来描述:y(n) = a * x(n) + (1-a) * y(n-1)其中,x(n) 是输入信号,y(n) 是输出信号,a 是一个常数,通常被称为滤波器系数,它的取值范围是 0 到 1。
当 a 接近于 1 时,滤波器对输入信号的影响就越大;当 a 接近于 0 时,滤波器对输入信号的影响就越小。
y(n-1) 是上一个时刻的输出信号,也就是滤波器的记忆。
一阶滤波算法可以被看作是一个低通滤波器,它的截止频率可以通过滤波器系数 a 来控制。
当 a 的取值较小时,滤波器的截止频率也会较小,从而可以滤除高频噪声;当 a 的取值较大时,滤波器的截止频率也会较大,从而可以保留信号中的高频成分。
二、一阶滤波算法的应用一阶滤波算法可以被广泛应用于各种领域,例如:1. 声音处理:一阶滤波器可以用来去除声音中的噪声,从而使得声音更加清晰、自然。
例如,当我们在使用手机录音时,就可以通过一阶滤波器来去除背景噪声,使得录音效果更加好。
2. 图像处理:一阶滤波器可以用来去除图像中的噪点,从而使得图像更加清晰、细腻。
例如,在数字相机中,就可以通过一阶滤波器来去除图像中的色彩噪点,使得照片更加美观。
3. 控制系统:一阶滤波器可以用来对控制系统中的信号进行滤波,从而使得系统更加稳定、可靠。
例如,在飞机上,就可以通过一阶滤波器来滤除飞机振动信号中的高频成分,从而使得飞机更加平稳、安全。
三、一阶滤波算法的优缺点一阶滤波算法作为一种基础算法,具有以下的优缺点:1. 优点:(1) 简单易用:一阶滤波算法的原理非常简单,可以很容易地实现。

一阶滤波方法范文一阶滤波方法是一种基本的信号处理方法,广泛应用于多个领域,包括电子工程、通信工程、控制系统等。
它通常用于去除信号中的高频成分或低频成分,以实现信号的平滑或高通/低通滤波的效果。
下面将介绍一阶滤波方法的基本原理、常见的滤波器类型和应用示例等内容。
一阶滤波方法的基本原理是基于一个简单的差分方程,其中当前时刻的输出值仅与当前时刻和上一时刻的输入值有关。
这种方法被称为一阶滤波器,因为它是一阶差分方程的离散版本。
一阶滤波器的传输函数具有一阶多项式的形式,通常表示为:H(z)=(z-a)/(z-b)其中z是复变量,a和b是滤波器的系数。
根据a和b的取值不同,一阶滤波器可以实现不同的滤波效果,包括高通、低通和带通滤波器等。
最常见的一阶滤波器类型是一阶低通滤波器和一阶高通滤波器。
一阶低通滤波器将高频成分抑制,只允许低频信号通过。
一阶高通滤波器则将低频成分抑制,只允许高频信号通过。
这两种滤波器都有不同的应用场景。
一阶低通滤波器通常用于平滑信号,去除噪声或快速变化的成分。
在控制系统中,一阶低通滤波器常用于减小传感器采样误差引起的高频振荡。
在音频信号处理中,一阶低通滤波器常用于去除高频噪声或实现平滑音量调节。
一阶高通滤波器常用于去除信号中的直流分量或低频成分。
在通信系统中,一阶高通滤波器可以用于去除信号中的直流偏移,提高信号的品质和可靠性。
在音频信号处理中,一阶高通滤波器可以用于提取音频信号中的高频成分,如人声或乐器的高音部分。
除了一阶低通和高通滤波器外,还有其他一些常见的一阶滤波器类型,如一阶带通滤波器和一阶带阻滤波器。
一阶带通滤波器可以选择指定频率范围内的信号通过,其他频率范围的信号被抑制。
一阶带阻滤波器则是选择指定频率范围外的信号通过,其他频率范围的信号被抑制。
这些滤波器类型在不同应用领域中都有广泛的应用。
为了实现一阶滤波方法,可以使用不同的工具和技术。
在模拟电路中,可以使用电容和电阻等元件构成一阶滤波器。
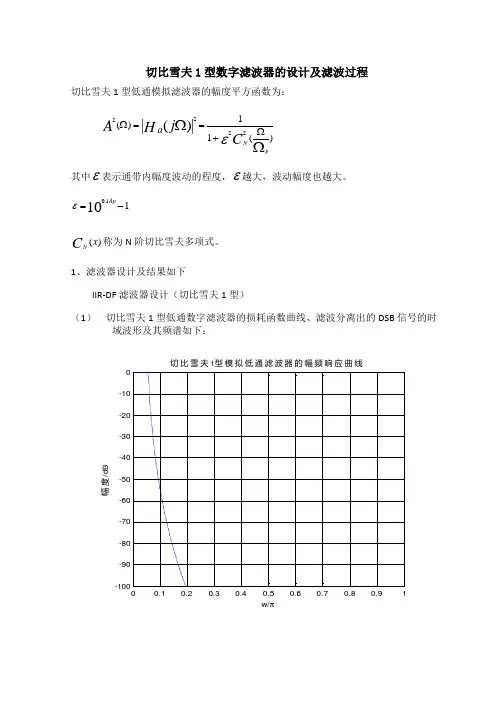
切比雪夫1型数字滤波器的设计及滤波过程切比雪夫1型低通模拟滤波器的幅度平方函数为:)(11)(2222|)(|ΩΩΩ+==ΩpNCj H Aa ε其中ε表示通带内幅度波动的程度,ε越大,波动幅度也越大。
1101.0-=Apε)(x CN称为N 阶切比雪夫多项式。
1、滤波器设计及结果如下IIR-DF 滤波器设计(切比雪夫1型)(1) 切比雪夫1型低通数字滤波器的损耗函数曲线、滤波分离出的DSB 信号的时域波形及其频谱如下:0.10.20.30.40.50.60.70.80.91-100-90-80-70-60-50-40-30-20-100w/π幅度/d B切比雪夫1型模拟低通滤波器的幅频响应曲线00.010.020.030.040.050.060.070.08-1-0.500.51t/sy 1(t )y1(t)的时域波形f/Hz幅度y1(t)的频谱其中阶数N=7(2) 切比雪夫1型带通数字滤波器的损耗函数曲线、滤波分离出的DSB 信号的时域波形及其频谱如下:0.10.20.30.40.50.60.70.80.91-100-90-80-70-60-50-40-30-20-100w/幅度/d B切比雪夫1型带通数字滤波器幅频响应曲线0.010.020.030.040.050.060.070.08-1-0.500.51t/sy 2(t )y2(t)的时域波形200400600800100012001400160018002000f/Hz幅度y2(t)的频谱其中阶数N=8(3)切比雪夫1型高通数字滤波器的损耗函数曲线、滤波分离出的DSB 信号的时域波形及其频谱如下:0.10.20.30.40.50.60.70.80.91-100-90-80-70-60-50-40-30-20-100w/幅度/d B切比雪夫1型高通数字滤波器幅频响应曲线0.010.020.030.040.050.060.070.08-1-0.500.51t/sy 3(t )y3(t)的时域波形f/Hz幅度y3(t)的频谱其中N=73、结果分析特点:误差值在规定的频段上等波纹变化。

一阶低通滤波c代码以下是一个简单的一阶低通滤波器的C代码实现。
一阶低通滤波器通常用于平滑数据,减少噪声。
它的工作原理是基于前一个输出样本和当前输入样本来计算新的输出样本。
请注意,以下代码假定你已经定义了一个合适的数据类型(如float),并且你的编译器支持基本的数学运算。
c#include <stdio.h>// 定义数据类型typedef float DataType;// 一阶低通滤波器结构体typedef struct {DataType alpha; // 滤波系数,取值范围0到1DataType prevOutput; // 上一次的输出值} FirstOrderLowPassFilter;// 初始化滤波器void initFilter(FirstOrderLowPassFilter *filter, DataType alpha) {filter->alpha = alpha;filter->prevOutput = 0.0;}// 应用滤波器DataType applyFilter(FirstOrderLowPassFilter *filter, DataType input) { DataType output = filter->alpha * input + (1.0 - filter->alpha) * filter->prevOutput;filter->prevOutput = output;return output;}int main() {FirstOrderLowPassFilter filter;DataType input, output;// 初始化滤波器,设置滤波系数为0.1initFilter(&filter, 0.1);// 假设我们有一个输入信号,这里用简单的for循环模拟for (int i = 0; i < 10; i++) {input = (i % 2 == 0) ? 10.0 : 0.0; // 模拟一个方波信号output = applyFilter(&filter, input);printf("Input: %f, Output: %f\n", input, output);}return 0;}以上代码首先定义了一个FirstOrderLowPassFilter结构体,它包含滤波系数alpha 和上一个输出值prevOutput。

数字低通滤波
数字低通滤波是一种信号处理技术,用于去除高频噪声,保留低频信号。
在数字信号处理中,低通滤波器是最常用的滤波器之一。
它可以应用于音频、图像、视频等领域,以提高信号质量和减少噪声。
数字低通滤波器的原理是将高频信号滤除,只保留低频信号。
在数字信号处理中,低通滤波器通常使用数字滤波器实现。
数字滤波器是一种将数字信号转换为另一个数字信号的系统。
数字滤波器可以分为两类:有限长冲激响应(FIR)滤波器和无限长冲激响应(IIR)滤波器。
有限长冲激响应滤波器是一种数字滤波器,其冲激响应是有限的。
这种滤波器的特点是稳定性好、相位响应线性、易于设计和实现。
有限长冲激响应滤波器的设计方法有窗函数法、频率抽样法、最小二乘法等。
无限长冲激响应滤波器是一种数字滤波器,其冲激响应是无限长的。
这种滤波器的特点是具有更好的频率响应特性,但相位响应不是线性的。
无限长冲激响应滤波器的设计方法有双线性变换法、频率变换法、极点零点法等。
数字低通滤波器的应用非常广泛。
在音频处理中,数字低通滤波器可以用于去除高频噪声,提高音频质量。
在图像处理中,数字低通滤波器可以用于去除图像中的高频噪声,使图像更加清晰。
在视频
处理中,数字低通滤波器可以用于去除视频中的高频噪声,提高视频质量。
数字低通滤波器是一种非常重要的信号处理技术。
它可以应用于音频、图像、视频等领域,以提高信号质量和减少噪声。
在实际应用中,我们需要根据具体的需求选择合适的数字低通滤波器,并进行适当的参数调整,以达到最佳的滤波效果。

一阶低通滤波器不同离散方法结果英文回答:A first-order low-pass filter is a type of analogfilter that allows low-frequency signals to pass through while attenuating high-frequency signals. It is a simple and commonly used filter due to its ease of implementation and low cost.There are two main methods for designing a first-order low-pass filter: the continuous-time (CT) method and the discrete-time (DT) method. The CT method designs the filter in the analog domain, while the DT method designs thefilter in the digital domain.The transfer function of a first-order low-pass filter is given by:H(s) = 1 / (1 + sRC)。
where:s is the complex frequency variable.R is the resistance in the filter.C is the capacitance in the filter.The cutoff frequency of the filter, which is the frequency at which the filter starts to attenuate the signal, is given by:f = 1 / (2πRC)。

将普通硬件RC低通滤波器的微分方程用差分方程来表求,变可以采用软件算法来模拟硬件滤波的功能,经推导,低通滤波算法如下:
Yn=a* Xn+(1-a)*Yn-1
式中Xn——本次采样值
Yn-1——上次的滤波输出值;
,a——滤波系数,其值通常远小于1;
Yn——本次滤波的输出值。
由上式可以看出,本次滤波的输出值主要取决于上次滤波的输出值(注意不是上次的采样值,这和加权平均滤波是有本质区别的),本次采样值对滤波输出的贡献是比较小的,但多少有些修正作用,这种算法便模拟了具体有教大惯性的低通滤波器功能。
滤波算法的截止频率可用以下式计算:
fL= a/2Pit pi为圆周率3.14…
式中a——滤波系数;
,t——采样间隔时间;
例如:当t=0.5s(即每秒2次),a=1/32时;
fL=(1/32)/(2*3.14*0.5)=0.01Hz
当目标参数为变化很慢的物理量时,这是很有效的。
另外一方面,它不能滤除高于1/2采样频率的干搅信号,本例中采样频率为2Hz,故对1Hz以上的干搅信号应采用其他方式滤除,
低通滤波算法程序于加权平均滤波相似,但加权系数只有两个:a和1-a。
为计算方便,a取一整数,1-a用256-a,来代替,计算结果舍去最低字节即可,因为只有两项,a和1-a,均以立即数的形式编入程序中,不另外设表格。
虽然采样值为单元字节(8位A/D)。
为保证运算精度,滤波输出值用双字节表示,其中一个字节整数,一字节小数,否则有可能因为每次舍去尾数而使输出不会变化。
设Yn-1存放在30H(整数)和31H(小数)两单元中,Yn存放在32H(整数)和33H(小数)中。

一阶低通滤波器有源低通滤波器计算利用R、L、C所组成的滤波电路称作无源滤波器,它有很多的缺点。
其中的电感L本身具有电阻与电容,使得输出结果会偏离理想值,而且会消耗电能。
若只利用R、C再附加放大器则形成主动滤波器,它有很多的优点,例如:不使用电感使得输出值趋近理想值;在带通范围能提高增益,减少损失;用放大器隔离输出、入端,使之可以使用多级串联。
1、一阶低通滤波器(一节RC网路)截止频率:频率低于时→电压增益频率高于时→衰减斜率:每10倍频率20dB图1 电路组成图2 响应曲线所谓低通滤波器(LPS:low pass filter)是允许低频讯号通过,而不允许高频讯号通过的滤波器。
图3所示是RC低通滤波电路,其电压回路公式:其增益可得实际增益为增益值是频率的函数,在低频区ω极小,RωC << 1,A V(ω) = 1讯号可通;在高频区ω极大,RωC >> 1,A V(ω) = 0信号不通。
RωC = 1时是通与不通的临界点,此时的频率定义为截止频率:。
图4所示RC低通滤波电路的增益随频率的变化是缓慢的,故其不是一个好的滤波电路。
图5所示是低通有源滤波器,它的增益显示在图6。
低通有源滤波器在低频区的增益为:V O/V I=(R1+R2)/R2其推导如下:在低频区RC串联之电位降都在电容,故V in = V C = Vp。
见图5,因负回馈,电路在线性工作区,于是我们有关系式:,可知电容C之电位降与电阻R2之电位降相同,又流过R1与R2之电流相同均为I,故得到在高频区RC串联之电位降都在电阻,故V C = V p = 0。
因负回馈,电路在线性工作区,于是有关系式:,得到R2之电位降为0,I = 0,V0 = 0。
图3 RC低通无源滤波电路图4 RC低通滤波电路之输出讯号振幅与频率的关系图5 低通有源滤波器图6 低通主动滤波器增益图7 理想的低通滤波器增益。

速度环常用滤波算法全文共四篇示例,供读者参考第一篇示例:速度环是一种常用的控制系统,在许多工程领域得到广泛应用,例如电动车辆控制、风力发电机控制、风扇调速等。
速度环的目的是使系统的输出速度达到期望值,从而实现系统的稳定工作。
在速度环控制中,滤波算法是非常重要的一环,它可以帮助系统减小噪声的影响,平滑系统输出并提高系统的稳定性。
目前,常用的速度环滤波算法包括低通滤波、卡尔曼滤波、中值滤波等。
下面我们将详细介绍一下这三种算法的原理和应用。
一、低通滤波算法低通滤波是最简单且常用的一种滤波算法。
其原理是通过减小信号中高频成分的幅值,以减少噪声的影响。
在速度环中,低通滤波算法可以使系统输出更加平滑,减小波动,并提高系统的响应速度和稳定性。
低通滤波算法的实现非常简单,通常采用一阶滤波器或者二阶滤波器。
一阶滤波器的传递函数为:H(s) = 1 / (Ts + 1)T为滤波器的时间常数,s为复频率变量。
通过调整时间常数T的大小,可以得到不同的滤波效果。
在实际应用中,可以通过实验确定最佳的T值,以满足系统的需求。
二、卡尔曼滤波算法卡尔曼滤波是一种用于估计系统状态的优化算法,在速度环中也得到了广泛的应用。
其原理是通过运用贝叶斯原理,将系统的状态以及对该状态的不确定性进行估计,从而实现最优的滤波效果。
卡尔曼滤波算法包括预测步骤和更新步骤。
预测步骤是根据系统的模型预测下一时刻的状态和不确定性,更新步骤是通过测量获得的信息来修正预测值,以得到更加准确的状态估计。
卡尔曼滤波算法具有较高的精度和鲁棒性,在速度环中可以有效地减小噪声的影响,并提高系统的稳定性和控制性能。
中值滤波算法的实现非常简单,只需将样本数据进行排序,然后取中间的值作为输出。
在实际应用中,可以通过改变样本数据的窗口大小来调整滤波效果,例如选择窗口大小为3或5可以获得可靠的滤波效果。
速度环常用的滤波算法包括低通滤波、卡尔曼滤波和中值滤波等。
这些算法可以帮助系统减小噪声的影响,平滑系统输出并提高系统的稳定性。

数字低通滤波器原理
数字低通滤波器是一种常用的信号处理工具,用于去除信号中高频成分,保留低频成分。
其原理基于采样定理和频域抽样。
根据采样定理,一个信号的最高频率成分不能超过其采样频率的一半。
在数字信号处理中,采样频率通常是已知的,因此可以根据需要选择一个截止频率来设计数字低通滤波器。
数字低通滤波器通过在频域对信号进行滤波,将高于截止频率的频谱成分去除。
常用的数字低通滤波器有FIR滤波器和IIR
滤波器。
FIR滤波器是一种非递归滤波器,其输出只依赖于输入和滤波
器的系数。
FIR滤波器的传递函数是一个有限长度的冲激响应,通过对输入信号与滤波器的冲激响应进行卷积运算来实现滤波。
IIR滤波器是一种递归滤波器,其输出不仅依赖于输入和滤波
器的系数,还依赖于其过去的输出。
IIR滤波器的传递函数是
一个有无穷长度的冲激响应,可以通过不同的结构实现,如直接形式、间接形式和级联形式。
设计数字低通滤波器需要选择适当的滤波器结构和滤波器参数。
常见的设计方法有窗函数法、频率采样法和最小均方误差法。
这些方法可以根据要求的滤波器性能来确定滤波器的系数。
最后,将输入信号通过数字低通滤波器进行处理,可以得到滤波后的信号,该信号去除了高于截止频率的高频成分,保留了
低频成分。
因此,数字低通滤波器在信号处理和通信系统中有着广泛的应用。
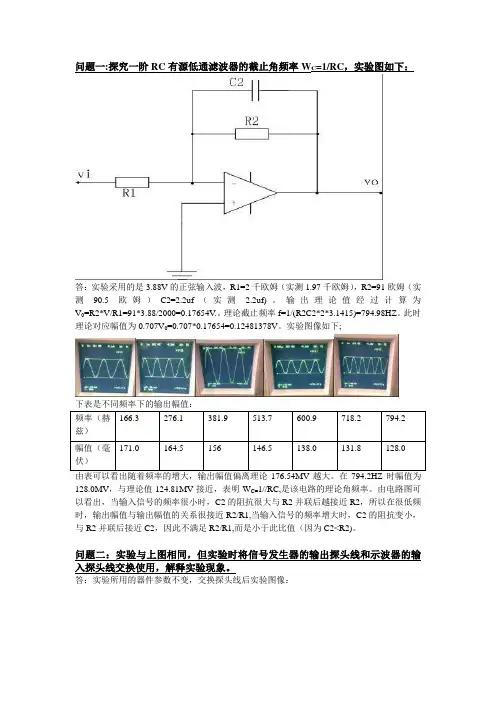
问题一:探究一阶RC有源低通滤波器的截止角频率W C=1/RC,实验图如下:答:实验采用的是3.88V的正弦输入波,R1=2千欧姆(实测1.97千欧姆),R2=91欧姆(实测90.5欧姆)C2=2.2uf(实测 2.2uf)。
输出理论值经过计算为V0=R2*V/R1=91*3.88/2000=0.17654V.。
理论截止频率f=1/(R2C2*2*3.1415)=794.98HZ。
此时理论对应幅值为0.707V0=0.707*0.17654=0.12481378V。
实验图像如下;下表是不同频率下的输出幅值:166.3 276.1 381.9 513.7 600.9 718.2 794.2频率(赫兹)171.0 164.5 156 146.5 138.0 131.8 128.0幅值(毫伏)由表可以看出随着频率的增大,输出幅值偏离理论176.54MV越大。
在794.2HZ时幅值为128.0MV,与理论值124.81MV接近,表明W C=1//RC,是该电路的理论角频率。
由电路图可以看出,当输入信号的频率很小时,C2的阻抗很大与R2并联后越接近R2,所以在很低频时,输出幅值与输出幅值的关系很接近R2/R1,当输入信号的频率增大时,C2的阻抗变小,与R2并联后接近C2,因此不满足R2/R1,而是小于此比值(因为C2<R2)。
问题二:实验与上图相同,但实验时将信号发生器的输出探头线和示波器的输入探头线交换使用,解释实验现象。
答:实验所用的器件参数不变,交换探头线后实验图像:下表是不同频率下的输出幅值:频率(赫兹)249.5 185.5 595 685.4 712 788 1000 2000幅值(毫伏)16.4 145.5 134.0 126.0 121.6 117.0 112.0 70.5由表可以看出,同上表具有相同的变化规律,即:随着输入信号的频率的增大,输出幅值呈减少趋势,与上表不同的是:输出幅值随信号频率增大而衰减的程度比实验一结果大,在685.4HZ时,就衰减到理论截止频率124.8MV左右。
这个问题基本解决了,谢谢楼上解释,下面是我的更详细的步骤对如图所示一阶低通滤波器,建立电路的微分方程:设输入电流i(t)则对输入端ui(t)=R*i(t)+1/C∫i(t)dt ------------------------1对输出端uo(t)= 1/C∫i(t)dt -------------------------2 2式两边微分得Cduo(t)/dt=i(t) -------------------------3将2,3带入1式得RCduo(t)/dt+uo(t)=ui(t) -------------------------4此即为一阶低通滤波器的微分方程。
对4式进行拉氏变换得sRCUo(s)+Uo(s)=Ui(s) -------------------------5其传导函数为G(s)=Uo(s)/Ui(s)=1/(1+sRC)=(1/RC)/(s+(1/RC))令ωc=1/RC, 则上式可写做G(s)=ωc/(s+ωc) --------------------------6令s=jω, 则由6H(jω)= ωc/( jω+ωc) ---------------------------7将7式分子分母同乘(ωc- jω)得H(jω)= ωc^2/(ωc^2+ω^2)-jωcω/(ωc^2+ω^2)其复角θ=arctan((-ωcω/(ωc^2+ω^2))/(ωc^2/(ωc^2+ω^2)))θ=-arctan(ω/ωc)此即为一阶低通滤波器的相频特性,当输入信号ω=截止频率ωc时,得=45°。
将4式写成差分形式得RC(uo(k)-uo(k-1))/T+uo(k)=ui(k)整理得uo(k)=uo(k-1)+T/RC(ui(k)-uo(k))其中:ωc=1/RC=2*pi*fc即uo(k)=uo(k-1)+T*2*pi*fc*(ui(k)-uo(k))此即为一阶低通滤波器的差分形式,可用于程序中对信号进行数字滤波。
篇一:[一阶低通滤波器]【我是工程师】从模拟到数字深入理解一阶RC低通滤波已更新~第一次发帖,跟在公司写报告一样,不知道如何从最简单的部分展开以及组织语言,大概列个框架,写写自己的理解,如果纰漏还请大神们指正~1、RC低通滤波时域分析2、RC低通滤波频域分析3、软件上常用滤波算法4、Z变换(离散化)没人看,自己继续~1、RC低通滤波时域分析不废话,先上图,典型的RC滤波电路如下电工们对此电路都极为熟悉吧,不管直流、交流、脉冲信号都可以用它,不管什么产品原理图上必定都有这个玩意,先从我们最初认识它的时域开始吧,尽管现在已经退化到看见一阶微分方程就想死的地步^^。
首先电容电流:根据基尔霍夫电压定律写出如下微分方程由于Vi的单位是V,所以RC的单位则是时间,也就是大家熟知的时间常数t=RC。
OK,至此大家是不是觉得一阶系统还是相当简单吧,那么如何求解这一阶微分方式还是交给数字本身吧,结果如下假设电容初始电压为0.Mathcad 计算如下一阶RC系统的阶跃响应曲线如下1 这么快就过去了,哎,放假的日子总是这么短暂,忧伤之余还是赶紧来更帖子~2、RC低通滤波频域分析图1简化如下,以电容电压为输出,电路的网络函数为令Wc即为截止频率。
则幅值和相角函数如下根据上边公式画出一阶RC低通滤波的幅频和相频特性曲线,Mathcad计算如下幅频特性曲线改用对数坐标如下如上幅频和相频特性曲线,当w<Wc时,幅值是平行与横坐标的直线,基本没有衰减。
当w>>Wc时,是斜率与-20dB/十倍频成比例的一条直线。
当w=Wc时,增益衰减至0.707,即-3dB,相位滞后45°,对于低通滤波器,该频率通常被称为截止频率。
人气不多,谢谢娜姐给上了首页,动力十足呀~频域大家搞电源的接触比较多,相对熟悉,我就埋个坑先从软件上常用的滤波算法说起吧。
3、软件上常用滤波算法当年还是菜鸟时,在网上流传有常用的10种软件滤波算法(最初源自21ic匠人之手),简单介绍如下1)限幅滤波法先根据经验判断,确定两次采样允许的最大偏差值,设为A。
低通滤波器低通滤波器的基本电路特点是,只允许低于截止频率的信号通过。
(1)一阶低通Butterworth滤波电路下图a和b是用运算放大器设计的两种一阶Butterworth滤波电路的电路。
图a是反相输入一阶低通滤波器,实际上就是一个积分电路,其分析方法与一阶积分电路相同。
基本滤波电路演示图b是同相输入的一阶低通滤波器。
根据给定的电路图可以得到对滤波器来说,更关心的是正弦稳态是的行为特性,利用拉氏变换与富氏变换的关系,有下图是上式RC=2时的幅频特性和相频特性波特图。
RC=2时一阶Butterworth低通滤波器的频率响应特性(2)二阶低通Butterworth滤波电路下图是用运算放大器设计的二阶低通Butterworth滤波电路。
二阶Butterworth低通滤波电路直接采用频域分析方法得到其中k = 1+R1/R2 。
令Q=1/(3-k),w0=1/RC,则可以写成其中k相当于同相放大器的电压放大倍数,叫做滤波器的通带增益,Q叫做品质因数,w0叫做特征角频率。
下图是二阶低通滤波器在RC=2时的波特图,其中图a是Q>0.707时的效果,图b是Q=0.707时的效果,图c是Q<0.707时的效果。
(a) Q>0.707(b) Q=0.707(c)Q<0.707二阶低通滤波器在RC=2时的波特图从图中可以看出,当Q>0.707 或Q<0.707时,通带边沿处会出现比较大的不平坦现象。
因此,品质因数表明了滤波器通带的状态。
一般要求Q=0.707。
由此可以得到这就是二阶Butterworth滤波器电压增益得计算0.707公式。
令Q=0.707,得0.414R2 = 0.707R1通常把最大增益倍所对应的信号频率叫做截止频率,这时滤波器具有3dB的衰减。
利用滤波器幅频特性的概念,可以得到截止频率w0 =w =1/RC,即f =1/2pRC高通滤波器的特点是,只允许高于截止频率的信号通过。
an1078 一阶数字低通滤波器推导和相位延迟
计算
一阶数字低通滤波器是一种常见的滤波器类型,用于去除信号中高频成分,保
留低频成分。
在数字信号处理中,一阶数字低通滤波器通常由差分方程描述,可以通过推导得到其频率响应和相位延迟。
首先,我们可以通过拉普拉斯变换将一阶低通滤波器的模拟原型转换为数字域。
一阶低通滤波器的模拟原型传递函数为H(s) = 1 / (s + ωc),其中ωc为截止频率。
通过双线性变换将传递函数转换为数字域的传递函数H(z),可以得到H(z) = (1 -
e^(-ωc*T)) / (1 - e^(-ωc*T)*z^(-1)),其中T为采样周期。
接下来,我们可以通过差分方程描述数字低通滤波器。
一阶数字低通滤波器的
差分方程形式为y[n] = (1 - α) * x[n] + α * y[n-1],其中α为滤波器的系数,通常为0到1之间的值,决定了滤波器的截止频率。
通过不断迭代差分方程,可以得到滤波器的频率响应。
为了计算一阶数字低通滤波器的相位延迟,我们可以通过频率响应来推导。
一
阶低通滤波器的频率响应为H(e^jω) = (1 - e^(-jω)) / (1 - e^(-jω)e^(-jωcT)),其中ω
为频率,ωc为截止频率,T为采样周期。
通过频率响应的相位,可以计算滤波器
的相位延迟。
综上所述,一阶数字低通滤波器的推导和相位延迳计算是通过频率响应和差分
方程来完成的。
通过推导滤波器的频率响应和差分方程,我们可以得到滤波器的特性,并计算出滤波器的相位延迟,从而更好地理解和应用一阶数字低通滤波器。
代码实现一阶数字低通滤波摘要:一、滤波原理介绍二、一阶数字低通滤波器的代码实现1.滤波器转移函数设计2.滤波器系数计算3.滤波器在Python中的实现三、滤波效果分析与验证四、应用场景及实际应用建议正文:一、滤波原理介绍数字低通滤波器是一种在数字信号处理中广泛应用的滤波器,主要用于去除高频噪声和保留低频信号。
一阶数字低通滤波器是数字低通滤波器的一种,其特点是过渡带宽较窄,通带内波动较小。
接下来我们将介绍如何实现一阶数字低通滤波器。
二、一阶数字低通滤波器的代码实现1.滤波器转移函数设计一阶数字低通滤波器的转移函数为:H(z) = 1 / (1 + ωs / ωp)其中,ωs为采样频率,ωp为截止频率。
2.滤波器系数计算根据转移函数,可以计算出滤波器的系数:a0 = 1 / (1 + ωs / ωp)a1 = -2 * ωs * a0b0 = 1 - a1b1 = -a03.滤波器在Python中的实现利用Python编写一阶数字低通滤波器的代码如下:```pythonimport numpy as npdef butter_lowpass(fs, fp, order=2):wn = np.pi * fp / fsb, a = signal.butter(order, wn, btype="low")return b, afs = 1000 # 采样频率fp = 50 # 截止频率order = 2 # 滤波器阶数b, a = butter_lowpass(fs, fp, order)```二、滤波效果分析与验证通过Matlab或其他信号处理工具,可以对滤波器进行仿真分析,观察滤波效果。
将上述Python代码在Matlab中运行,可得到滤波后的信号。
通过对比原始信号和滤波后的信号,可以验证滤波器的效果。
三、应用场景及实际应用建议一阶数字低通滤波器广泛应用于各种信号处理场景,如图像处理、声音处理等。
一阶滤波器的阻尼比摘要:一、一阶滤波器的概念二、一阶滤波器的阻尼比三、一阶滤波器的应用四、一阶滤波器的设计五、一阶滤波器的性能分析六、一阶滤波器与其他滤波器的比较七、一阶滤波器的发展趋势正文:一、一阶滤波器的概念一阶滤波器,又称一阶低通滤波器,是一种最基本的数字滤波器。
它的主要作用是去除信号中的高频干扰,保留信号的低频部分。
在实际应用中,一阶滤波器常用于信号处理、控制系统、通信系统等领域。
二、一阶滤波器的阻尼比阻尼比是衡量一阶滤波器性能的一个重要参数。
它表示了滤波器对信号的衰减程度,决定了滤波器在抑制干扰信号的同时,对信号的衰减程度。
阻尼比的计算公式为:阻尼比= 滤波器的传递函数的零点/ 滤波器的传递函数的极点。
三、一阶滤波器的应用在信号处理领域,一阶滤波器常用于去除图像、声音等信号中的高频干扰。
在控制系统,一阶滤波器用于系统的速度环、位置环等环节,以提高系统的稳定性和精度。
在通信系统中,一阶滤波器用于去除噪声、干扰信号,提高信号的传输质量。
四、一阶滤波器的设计设计一阶滤波器的主要步骤包括:确定滤波器的类型、选择滤波器的截止频率、设计滤波器的传递函数、分析滤波器的性能。
在设计中,需要关注的参数包括:截止频率、阻尼比、滤波器的阶数等。
五、一阶滤波器的性能分析一阶滤波器的性能分析主要包括:频率响应分析、稳定性分析、逼近性能分析等。
通过这些分析方法,可以评估一阶滤波器在实际应用中的性能优劣。
六、一阶滤波器与其他滤波器的比较一阶滤波器与其他滤波器(如二阶滤波器、高阶滤波器)相比,具有结构简单、计算复杂度低、容易实现等优点。
但同时,一阶滤波器的性能也相对较差,对信号的衰减程度较小,对高频干扰的抑制能力较弱。
七、一阶滤波器的发展趋势随着科技的进步,一阶滤波器在技术上不断发展和创新。
将普通硬件RC低通滤波器的微分方程用差分方程来表求,变可以采用软件算法来模拟硬件滤波的功能,经推导,低通滤波算法如下:
Yn=a* Xn+(1-a)*Yn-1
式中Xn——本次采样值
Yn-1——上次的滤波输出值;
,a——滤波系数,其值通常远小于1;
Yn——本次滤波的输出值。
由上式可以看出,本次滤波的输出值主要取决于上次滤波的输出值(注意不是上次的采样值,这和加权平均滤波是有本质区别的),本次采样值对滤波输出的贡献是比较小的,但多少有些修正作用,这种算法便模拟了具体有教大惯性的低通滤波器功能。
滤波算法的截止频率可用以下式计算:
fL= a/2Pit pi为圆周率3.14…
式中a——滤波系数;
,t——采样间隔时间;
例如:当t=0.5s(即每秒2次),a=1/32时;
fL=(1/32)/(2*3.14*0.5)=0.01Hz
当目标参数为变化很慢的物理量时,这是很有效的。
另外一方面,它不能滤除高于1/2采样频率的干搅信号,本例中采样频率为2Hz,故对1Hz以上的干搅信号应采用其他方式滤除,
低通滤波算法程序于加权平均滤波相似,但加权系数只有两个:a和1-a。
为计算方便,a取一整数,1-a 用256-a,来代替,计算结果舍去最低字节即可,因为只有两项,a和1-a,均以立即数的形式编入程序中,不另外设表格。
虽然采样值为单元字节(8位A/D)。
为保证运算精度,滤波输出值用双字节表示,其中一个字节整数,一字节小数,否则有可能因为每次舍去尾数而使输出不会变化。
设Yn-1存放在30H(整数)和31H(小数)两单元中,Yn存放在32H(整数)和33H(小数)中。