第2讲 效用函数与需求函数
- 格式:ppt
- 大小:1.14 MB
- 文档页数:54


平新乔《微观经济学十八讲》第2讲 间接效用函数与支出函数1.设一个消费者的直接效用函数为12ln u q q α=+。
求该消费者的间接效用函数。
并且运用罗尔恒等式去计算其关于两种物品的需求函数。
并验证:这样得到的需求函数与从直接效用函数推得的需求函数是相同的。
解:(1)①当20y p α->时,消费者的效用最大化问题为:12122,112m ln ax q q s t q p p yq q q α..+=+构造拉格朗日函数:()121122ln L q q q y p p q αλ--=++L 对1q 、2q 和λ分别求偏导得:1110L p q q αλ∂=-=∂ ① 2210Lp q λ∂=-=∂ ② 11220q Ly p p q λ∂=--=∂ ③ 从①式和②式中消去λ后得:211p q p α*=④再把④式代入③式中得:222y p p q α*-=⑤ 从而解得马歇尔需求函数为:211p q p α*=222y p p q α*-=由⑤式可知:当20y p α->时,20q *>,消费者同时消费商品1和商品2。
将商品1和商品2的马歇尔需求函数代入效用函数中得到间接效用函数:()()2112122,,,ln p v p p y p q q y u p ααα**=+-=②当20y p α-≤时,消费者只消费商品1,为角点解的情况。
从而解得马歇尔需求函数为:11q y p *=20q *= 将商品1和商品2的马歇尔需求函数代入效用函数中得到间接效用函数:()()12121,,,ln v p p y u q p y q α**== (2)①当20y p α->时,此时的间接效用函数为:()()2112122,,,lnp v p p y p q q yu p ααα**=+-= 将间接效用函数分别对1p 、2p 和y 求偏导得:11v p p α∂=-∂ 2222v y p p p α∂=-∂ 21v y p ∂=∂ 由罗尔恒等式,得到:1112121v p p p v y p q p αα*∂∂=-==∂∂ 222222221y p v p p y p y q v p p αα*-∂∂-=-==∂∂②当20y p α-≤时,间接效用函数为()()12121,,,lnv p p y u q p yq α**==,将间接效用函数分别对1p 、2p 和y 求偏导得:11v p p α∂=-∂ 20v p ∂=∂ v y yα∂=∂ 由罗尔恒等式,得到:1111v p p y v y p yq αα*∂∂=-==∂∂ 2200v p v y y q α*∂∂=-==∂∂ (3)比较可知,通过效用最大化的方法和罗尔恒等式的方法得出的需求函数相同。

需求函数,收入效应和替代效应:理论和实证David Autor14.03 2004 秋季1马歇尔需求中的价格变化●消费者预算的微小变化(即I的上升或者下降)都涉及到消费线自原始位置向内或向外平行移动。
这样的经济学是很简单的。
既然这样的移动保持了价格比率,那么它对消费者的边际替代率(MRS)就没有任何影响,,除非选定的商品组合在一开始或者最终处于边角解答中。
●保持其他商品价格和收入不变,一种商品的价格上升在经济学上有着更复杂的效应:— 它使得预算线由原始位置向内移动了。
换言之,消费者现在更穷了。
与之相对的是“收入效应”。
— 它改变了预算线的斜率,这样消费者就面临了一个不同的市场交易比率。
与之相对的是“价格效应”。
●尽管两种移动是同时发生的,但它们的概念是有区别的,而且对消费者行为而言也存在不同的含意。
1.1收入效应首先,考虑“收入效应”。
在一个两商品的经济体中,预算线由原始位置向内移动有什么影响:1.总消费?[下降]2.效用?[下降]3.对的消费?[答案取决于是正常物品或是低档物品]4.对的消费?[答案取决于是正常物品或是低档物品]1.2替代效应●在同一个两商品的经济体中,对的消费会有什么变化,若:而且效用保持不变?●换句话说,我们想要得出:●在应用MRS递减公理的情况下,我们有●总之,保持效用不变,替代效应总是负的。
●相反地,按照上面的推理,收入效应的符号却是不确定的,取决于是正常物品还是低档物品。
1.3商品的类型替代效应总是负的而收入效应却是不确定的,这就引出了三种类型的商品的划分:1.正常物品:。
对于这种商品,价格的上升和收入的下降有着相同的影响 — 更少的消费量。
尽管只观察了从到的移动,我们也能理解这种移动由两个部分组成:从到的移动(替代效应)和从到的移动(收入效应)。
2.低档物品:。
对于这种商品,收入和替代效应是相互抵消的。
为什么?甚至于尽管导数是同号的,它们的效应也是相反的。
因为价格的上升减少了实际收入 — 从而通过收入效应增加了消费,即便是替代效应同时也使消费减少。







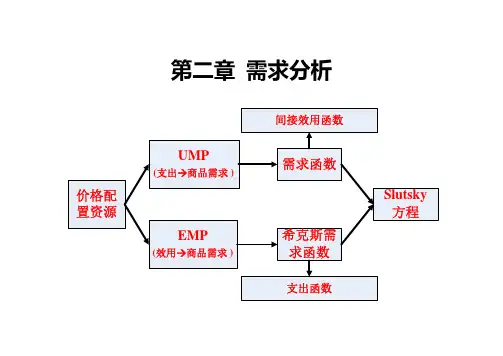
第二章需求分析一、需求函数(一)瓦尔拉斯需求函数商品需求定义:预算集中的效用最大化的解X *,反映*x 与P 与W 的关系称为需求函数,表示成n w +∈R p x ),(。
例子:建立L 函数:)()(),,(221112121x p x p w x x x x L --++==λλρρρ 一阶条件为:0)(111111211=-+=∂∂--p x x x x L λρρρρρρ 0)(121211212=-+=∂∂--p x x x x L λρρρρρρ 02211=--=∂∂x p x p w Lλ21121)(p p x x =-ρ,直接推导112121122111)(---=⇒=ρρρp p x x x p p x代入2211x p x p w +=,得到:121111111211211112112121)()(--------+=+==ρρρρρρρρρρρρp p wp p pp p wp p px x ;12111122---+=ρρρρρp p wp x令1-=ρρr ,则有:r r r p p wp x 21111+=-,rr r p p wp x 21122+=-需求函数的三个性质(1)在价格和收入上,需求函数是零次齐次的:即对于任给p ,w 和满足0>a ,有),(),(w p x aw ap x =经济含义是:如果价格和收入以同一比例变化,则消费者的需求数量保持不变。
(2)瓦尔拉斯法则:任给),(w p x x ∈有w x p =⋅经济含义:消费者会在有生之年用光他的全部资源(财富)。
(3)凸性和唯一性。
如果)(⋅u 是拟凹的,则),(w p x 是一个凸集。
思考如何证明。
若)(⋅u 是严格拟凹的,则),(w p x 只包含单一的元素。
(二)间接效用函数定义:)],([),(*w p x u w p v =,即需求函数代入原效用函数。
例子:2121ln )1(ln ),(x x x x u αα-+= s.t. w x p x p =+2211 构造拉格朗日函数:()()221121ln 1ln x p x p w x x L --+-+=λαα 一阶条件: 01111=-=∂∂p x x L λα (1);()011222=--=∂∂p x x L λα (2)02211=--=∂∂x p x p w Lλ(3) ()()2112121p p x x =-⋅⇒αα 12211p p x x ⋅-⋅=αα (4) 或21121p p x x ⋅-⋅=αα (5)将(5)代入(3) w x p x p w p p x p x p =⋅-+⇒=⋅-+111121121111αααα111111111p w x w x p w x p αααα=⇒=⋅⎪⎭⎫ ⎝⎛⇒=⋅⎪⎭⎫ ⎝⎛-+将(4)代入(3)w x p x p w x p p p x p =+-⋅⇒=+⋅-⋅222222122111αααα()22222211111p w x w x p w x p αααα-=⇒=⎪⎭⎫ ⎝⎛-⇒=⎪⎭⎫ ⎝⎛+-然后求解间接效用函数:将需求函数代入目标函数:2121ln )1(ln ),(x x x x u αα-+=()21211ln)1(ln),,(p wp ww p p v αααα--+=()()[]21ln ln 1ln )1(ln ln ln p w p w -+--+-+=αααα()()()()21ln 1ln 11ln 1ln ln ln p w p w αααααααα---+--+-+=()()()αααααα--++---=1ln 1ln ln 1ln ln 21p p w∴c p p w w p p v +---=2121ln )1(ln ln ),,(αα 其中:)1ln()1(ln αααα--+=c 。
已知马歇尔需求函数求效用函数
马歇尔需求函数又称为巴科斯函数,是经济学里最重要的基本函数之一,其定义为消费者估计消费支出,其根据消费者的财富来定义,用符号表示为Q = f(m),其中Q代表消费量,m表示财富。
马歇尔需求函数的特性为正相关,即增加财富会使消费支出增加,减少财富则消费支出减少。
由马歇尔需求函数求效用函数,可以把效用函数U定义为对消费者消费支出的效用。
由马歇尔需求函数Q=f(m),可以得到以下效用函数:U=f(Q) 。
效用函数U反映了受资源和消费者现有财富限制,消费者在一定财富下所获得的收益度,或者说物品所获得的效用。
效用函数为消费者在物品的需求时的决策做出指导,也会对消费者的选择产生影响。
总结下来,从马歇尔需求函数能求出效用函数,其定义为消费者估计消费支出,其根据消费者的财富来衡量,可以反映消费者在一定财富下所获得的收益度,或者说物品所获得的效用,对消费者的选择产生影响。
高鸿业版西方经济学(微观部分)名词解释价格:价格是经济参与者之间相互联系和传递经济信息的机制。
需求:指消费者在一定时期内在各种可能的价格水平下愿意而且能够购买的商品数量。
需求函数:是表示一种商品的需求数量和影响该需求数量的各种因素之间的相互关系。
需求表:是表示某种商品的各种价格水平和与各种价格水平相对应的该商品的需求数量之间的数字序列表。
供给:是指生产者在一定时期内在各种可能的价格水平下愿意而且能够提供出售的该种商品的数量。
供给函数:表示一种商品的供给量和该商品价格之间存在着一一对应的关系。
供给表:是表示某种商品的各种价格和与各种价格相对应的该商品的供给数量之间关系的数字序列表。
均衡:指经济事物中有关的变量在一定条件的相互作用下所达到的一种相对静止的状态。
局部均衡:是就单个市场或部分市场的供求与价格之间的关系和均衡状态进行分析。
一般均衡:是就一个经济社会的所有市场的供求与价格之间的关系好均衡状态进行分析。
均衡价格:指一种商品的市场需求量和市场供给量相等时的价格。
均衡数量:在均衡价格水平下的相等的供求数量。
市场出清:市场上需求量与供给量相等的状态。
需求量的变动:是指在其他条件不变时,由商品的价格变动所引起的该商品的需求数量的变动。
需求的变动:是指在某商品价格不变的条件下,由于其他因素变动所引起的该商品的需求数量的变动。
供给量的变动:是指在其他条件不变时,由某商品的价格变动所引起的该商品供给数量的变动。
供给的变动:是指在某商品价格不变的条件下,由于其他因素变动所引起的该商品的供给数量的变动。
供求定理:在其他条件不变的情况下,需求变动分别引起均衡价格和均衡数量的同方向的变动;供给变动引起均衡价格的反方向的变动,引起均衡数量的同方向的变动。
经济理论:是在对现实的经济事物的主要特征和内在联系进行概括和抽象的基础上,对现实的经济事物进行的系统描述。
经济模型:是指用来描述所研究的经济事物的有关经济变量之间相互关系的理论结构。
效⽤最⼤化问题中的三个函数——需求函数、间接效⽤函数、⽀出函数需求函数:性质:关于所有价格和收⼊零次齐次性(所有商品价格与收⼊乘以t倍),最优化需求数量保持不变。
1. CES需求函数CES需求函数的函数形式为:构造朗格朗⽇表达式:求偏导数得到⼀阶条件:根据上式求得需求函数:从上式看出我们确实可以得到⼀个对于任意的CES函数的需求函数。
但是个⼈建议,由于CES函数有不同的“形式”(⽐如说也是⼀种CES函数,所以在实际做题求解CES函数的需求函数的过程中,建议重复上述证明步骤,⽤构造拉格朗⽇表达式,利⽤⼀阶条件来求解需求函数)当的时候,此时为完全互补效⽤函数,利⽤消费者为了效⽤最⼤化只会选择L型⽆差异曲线顶点消费的特征来直接求解,就不⽤构造朗格朗⽇表达式了。
除此之外,联系弹性和之前讲过的(点击链接回顾)的概念,我们不难发现,,即替代弹性等于1为分界线。
举例说明:当的时候,此时商品x花费的收⼊份额为不是常数,越⾼,x的相对价格越⾼,它所花费的收⼊份额就越⼩。
换⾔之,x的需求对其价格的反应就⾮常敏感,价格的上升减少了x的总花费。
不过收⼊的变化并不影响消费份额。
U (x ,y )=+δx δδy δf =+δx δ+δy δλ(I −p x −x p y )y ⎩⎨⎧=x −λp =0∂x ∂f δ−1x =x −λp =0∂x∂f δ−1x =I −p x −p y =0∂λ∂f x y ⎩⎨⎧x =p (1+())x p y p x 1−δδy =p (1+())y p x p y 1−δδI δU =(αx +11ραx )22ρρ1δ→∞δ=0σ=1−δ1δ=0.5x =p (1+())x p y p x I p x /I =x 1/[1+(p /p )]x y p x2. 柯布道格拉斯需求函数柯布-道格拉斯效⽤函数的表达式为:同样可以利⽤朗格朗⽇法来算出需求函数,由于过程重复,在此不做赘述,得到如下的结果:由此我们得到⼀个重要的结论,在柯布道格拉斯效⽤函数情形下,消费者会花费⽐例的收⼊去购买商品x,⽤的⽐例去购买y。