当前位置：文档之家 › 第一章 逻辑代数基础

第一章 逻辑代数基础

  • 格式：doc
  • 大小：89.50 KB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

数字电路：第一章 逻辑代数基础

数字电路：第一章 逻辑代数基础

1•A=A 0+A=A
AB+AC+BC=AB+AC (A+B)(A+C)(B+C) = (A+B)(A+C)
§1—5 用代数法化简逻辑式
最简与或表达式： 1、乘积项的个数最少(用门电路实现，用
的与门数最少)。 2、在满足1的条件下，乘积项中的变量最少
(与门的输入端最少)。 省器件：用最少的门，门的输入也最少
“异或”门电路的用处
(1)可控的数码原/反码输出器 A0=A A1=A
(2)作数码同比较器 (3)求两数码的算术和
AB F 00 0 01 1 10 1 11 0
§1—4 基本规则
1）代入规则： A•B=A+B 用A=CD代替A,等式仍成立
CD•B=CD+B=C+D+B 2)反演规则：
F: 若：“•”“+”,“+”“•”,“0”“1”,“1”“0” 原变量反变量，反变量原变量
A B
F
F=AB AC ACD BD
A B
1
C
1
D
“与非”表达 式
&
&
&
F
&
&
2、“或非” F=A+B+C
A
A
B >1 C
FB C
+
F
F=A+B+A+C+D+B+D
“或非”表达 式
3、“与或非” F=AB+CD
A & >1 B C D
A
F
B C
D
+F

数字电路(第一章逻辑代数基础)

数字电路(第一章逻辑代数基础)
数字电路技术基础
东南大学计算机系
电话： 025-3792757 Email：qqliu@
刘其奇
1
第一章 逻辑代数基础
1-1 概述
1-1-1 数字量和模拟量
自然界中物理量分为两大类：
数字量：它们的变化在时间上和数量上都是离散的； 在时间上不连续。
模拟量：它们的变化在时间上或数值上是连续的。 数字信号：表示数字量的信号，是在两个稳定状态之 间作阶跃式变化的信号。 脉冲：是一个突然变化的电压或电流信号。
11
有权码
常用BCD码 十进制数
0 1 2 3 4 5 6 7 8 9
无权码
8421BCD
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001
5421BCD
0000 0001 0010 0011 0100 1000 1001 1010 1011 1100
22
2）变量常量关系定律
0、 1律：A • 1 = A; (2 )
A • 0 = 0;（1）
A + 1 = 1; （11） A + 0 = A（12） ;
互补律：A • A = 0； ） A + A = 1;（14） （4
3）逻辑代数的特殊定律
重叠律：A • A = A； ） A + A = A; （13） （3
Y = A + A BC( A + BC + D) + BC = A + ( A + BC)( A + BC + D) + BC = A + A ( A + BC + D) + BC( A + BC + D) + BC = A + BC

逻辑代数基础

逻辑代数基础

第一章逻辑代数基础1.1概述1.1.1模拟信号和数字信号电子电路中的信号可以分为两大类：模拟信号和数字信号。

模拟信号——时间连续、数值也连续的信号。

数字信号——时间上和数值上均是离散的信号。

（如电子表的秒信号、生产流水线上记录零件个数的计数信号等。

这些信号的变化发生在一系列离散的瞬间，其值也是离散的。

）数字信号只有两个离散值，常用数字0和1来表示，注意，这里的0和1没有大小之分，只代表两种对立的状态，称为逻辑0和逻辑1，也称为二值数字逻辑。

数字电路的特点和分类传递与处理数字信号的电子电路称为数字电路。

1、数字电路的特点数字电路与模拟电路相比主要有下列优点：（1）由于数字电路是以二值数字逻辑为基础的，只有0和1两个基本数字，易于用电路来实现，比如可用二极管、三极管的导通与截止这两个对立的状态来表示数字信号的逻辑0和逻辑1。

（2）由数字电路组成的数字系统工作可靠，精度较高，抗干扰能力强。

它可以通过整形很方便地去除叠加于传输信号上的噪声与干扰，还可利用差错控制技术对传输信号进行查错和纠错。

（3）数字电路不仅能完成数值运算，而且能进行逻辑判断和运算，这在控制系统中是不可缺少的。

（4）数字信息便于长期保存，比如可将数字信息存入磁盘、光盘等长期保存。

（5）数字集成电路产品系列多、通用性强、成本低。

由于具有一系列优点，数字电路在电子设备或电子系统中得到了越来越广泛的应用，计算机、计算器、电视机、音响系统、视频记录设备、光碟、长途电信及卫星系统等，无一不采用了数字系统。

2、数字电路的分类按集成度分类：数字电路可分为小规模（SSI，每片数十器件）、中规模（MSI，每片数百器件）、大规模（LSI，每片数千器件）和超大规模（VLSI，每片器件数目大于1万）数字集成电路。

集成电路从应用的角度又可分为通用型和专用型两大类型。

1.1.2 数制与码制1. 数制一．几种常用的计数体制1、十进制(Decimal)数码为：0～9；基数是10。

第1章 逻辑代数基础

第1章 逻辑代数基础
5、三个重要运算规则
①代入规则：任何一个含有变量 A 的等式，如果将所有出现 A 的位置都用
同一个逻辑函数代替，则等式仍然成立。这个规则称为代入规则。 例如，已知等式 AB A B ，用函数 Y=AC 代替等式中的 A，
根据代入规则，等式仍然成立，即有：
( AC) B AC B A B C
A
E
B Y
4
第1章 逻辑代数基础---三种基本运算
功能归纳：
真值表：
开关 A 开关 B 断开 断开 闭合 闭合 断开 闭合 断开 闭合
灯Y 灭 灭 灭 亮
A 0 0 1 1
B 0 1 0 1
Y 0 0 0 1
将开关接通记作1，断开记作0；灯亮记作1，灯灭记作0。可以作出如
上表格来描述与逻辑关系，这种把所有可能的条件组合及其对应结果一一列
的逻辑函数， 并记为：
F f ( A, B, C , )
3
第1章 逻辑代数基础---三种基本运算
②三种基本运算
a.与逻辑（与运算）
定义:仅当决定事件（Y）发生的所有条件（A，B，C，…）均满足 时，事件（Y）才能发生。表达式为：
Y=A· C· B· …=ABC…
描述:开关A，B串联控制灯泡Y
法进行描述。每种方法各具特点，可以相互转换。 ①真值表
将输入变量的各种可能取值和相应的函数值排列在一起而组成的表格。
真值表列写方法：每一个变量均有0、1两种取值，n个变量共有2n种不 同的取值，将这2n种不同的取值按顺序（一般按二进制递增规律）排列起
来，同时在相应位置上填入函数的值，便可得到逻辑函数的真值表。
原式左边
AB A C ( A A ) BC

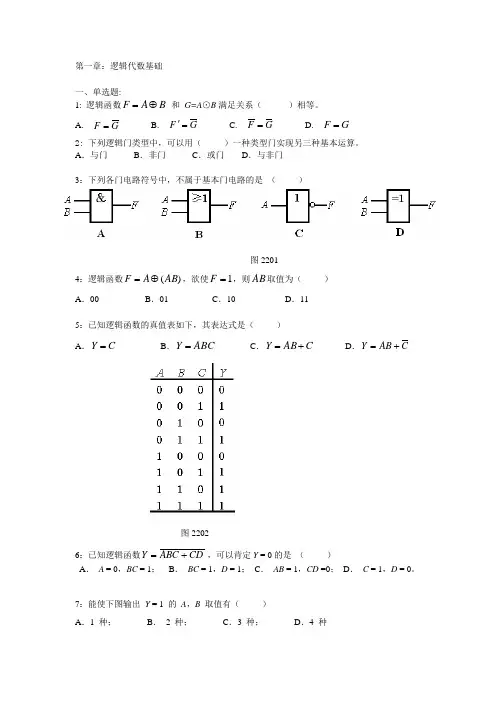
01A第一章 逻辑代数基础

01A第一章 逻辑代数基础

正、负逻辑：在实际应用中，器件的输入、输出量用逻辑电平表示， 负逻辑：在实际应用中，器件的输入、输出量用逻辑电平表示，
正逻辑：用高电平表示逻辑1 低电平表示逻辑0 正逻辑：用高电平表示逻辑1，低电平表示逻辑0 负逻辑：用低电平表示逻辑1 高电平表示逻辑0 用图表示） 负逻辑：用低电平表示逻辑1，高电平表示逻辑0（用图表示）
四 二进制代码
编码 ：用二进制数表示文字、符号等信息的过程 用二进制数表示文字、 二进制代码： 二进制代码：用来进行编码之后的二进制数
8421BCD码（ Binary Coded Decimal Codes）为十进制数的二进制编码形式 码 ）
8421码 码
十进制码
8421码 码
十进制码 伪码(冗余码 伪码 冗余码) 冗余码 伪码(冗余码 冗余码) 伪码 冗余码 伪码(冗余码 冗余码) 伪码 冗余码 伪码(冗余码 冗余码) 伪码 冗余码 伪码(冗余码 冗余码) 伪码 冗余码 伪码(冗余码 冗余码) 伪码 冗余码
若用逻辑表达式 来描述， 来描述，则可写为
L = A ⋅B 或L = AB
与运算——只有当决定一件事情的条件全部具备之后， 与运算 只有当决定一件事情的条件全部具备之后，这件事情 只有当决定一件事情的条件全部具备之后 才会发生。我们把这种因果关系称为与逻辑 与逻辑。 才会发生。我们把这种因果关系称为与逻辑。 总结： 总结：有0出0，全1出1
1.3基本逻辑运算和基本逻辑门 基本逻辑运算和基本逻辑门
一、 基本逻辑运算
1．与运算 与逻辑举例： 与逻辑举例：首先逻辑赋值 表示开关闭合和灯亮； 设1表示开关闭合和灯亮； 0表示开关不 闭合和灯不亮， 闭合和灯不亮， 则得真值表 真值表。 则得真值表。
这种以列表的方式来真实的反映出输出和输入变量的正确关系的方法叫 做图形法或真值表法。 做图形法或真值表法。 真值表的情况有2 是输入变量个数， 真值表的情况有 n种，n是输入变量个数，列真值表时应将各种可能的 是输入变量个数 情况都列进去，顺序可以随意，但是最好按照十进制的顺序来列，以免漏掉。 情况都列进去，顺序可以随意，但是最好按照十进制的顺序来列，以免漏掉。

1第一章知识资料逻辑代数基础

1第一章知识资料逻辑代数基础

0 A=0 1+A=1
A A=0 A+A=1
2、定理
A+A=A A•A=A
A=A
(德•摩根定律)
A•B=A+B A+B=A•B
交换律 A B=B A A+B=B+A
A B A•B A+B 00 1 1 01 1 1 10 1 1 11 0 0
结合律 A (B C)=(A B) C A+(B+C)=(A+B)+C
数字电路的特点
（3）在两种电路中，晶体管的工作状态不同。 数字电路中晶体管工作在开关状态，也就 是交替地工作在饱和与截止两种状态，而 在模拟电路中晶体管多工作在放大状态。
（4）数字电路采用二进制，主要分析工具是逻 辑 代数，而模拟电路采用十进制，主要分析工 具是普通代数。
数字电路的分类
分立元件 按电路组成结构
F2=A+BD+ABCD F2=A•(B+D)•(A+B+C+D)
三、对偶规则： F: 若：“•”“+”,“+”“•”,“0”“1”,“1”“0” 则：FF F与F互为对偶函数 如果两个函数相等，则它们的对偶函数也相等。 函数对偶式的对偶式为函数本身。
1•A=A 0+A=A
AB+AC+BC=AB+AC (A+B)(A+C)(B+C) = (A+B)(A+C)
CBA
m1
CBA
m5
CBA
m2
CBA
m6
CBA
m3
CBA
m7
最小项的性质
1)最小项为“1”的取值唯一。 如：最小项ABC,只有ABC取值101时， 才为“1”，其它取值时全为“0”。

第一章：逻辑代数基础

第一章：逻辑代数基础

第一章：逻辑代数基础一、单选题:1: 逻辑函数B A F ⊕= 和 G=A ⊙B 满足关系（ ）相等。

A. G F = B. G F =' C. G F = D. G F = 2: 下列逻辑门类型中，可以用（ ）一种类型门实现另三种基本运算。

A ．与门 B ．非门 C ．或门 D ．与非门3：下列各门电路符号中，不属于基本门电路的是 （ ）图22014：逻辑函数)(AB A F ⊕=，欲使1=F ，则AB 取值为（ ） A ．00B ．01C ．10D ．115：已知逻辑函数的真值表如下，其表达式是（ ）A ．C Y =B ．ABC Y = C ．C AB Y +=D ．C AB Y +=图22026：已知逻辑函数 CD ABC Y +=，可以肯定Y = 0的是 （ ）A ． A = 0，BC = 1；B ． BC = 1，D = 1； C ． AB = 1，CD =0； D ． C = 1，D = 0。

7：能使下图输出 Y = 1 的 A ，B 取值有（ ）A ．1 种；B ． 2 种；C ．3 种；D ．4 种图22038：下图电路，正确的输出逻辑表达式是（ ）。

A ． CD AB Y += B ． 1=YC ． 0=YD ． D C B A Y +++=图22049：根据反演规则，E DE C C A Y ++⋅+=)()(的反函数为（ ） A. E E D C C A Y ⋅++=)]([ B. E E D C C A Y ⋅++=)( C. E E D C C A Y ⋅++=)( D. E E D C C A Y ⋅++=)(10：若已知AC AB C A B A =+=+,，则（ ）A ． B=C = 0B ． B=C =1 C ． B=CD ． B ≠C11：在什么情况下，“与非”运算的结果是逻辑0。

（ ）A ．全部输入是0 B. 任一个输入是0 C. 仅一个输入是0 D. 全部输入是112：逻辑函数=⊕⊕=)(B A A F （ ）A ．B B ．AC ．B A ⊕D ． B A ⊕13：逻辑式=⋅+⋅+A A A 10 （ ）A ． 0B ． 1C ． AD ．A14：逻辑函数ACDEF C AB A Y +++=的最简与或式为（ ）A ．C A Y += B.B A Y += C. AD Y = D. AB Y =15：下列逻辑函数中不相等的是（ ）。

逻辑代数基础(课件)

逻辑代数基础(课件)

图形符号
A
L
B
23
2. 或逻辑
逻辑表达式 L= A + B
只有决定某一事件的原因有一个或 一个以上具备，这一事件才能发生
AB L 00 0 01 1 10 1 11 1 或逻辑真值表
图形符号
A 1
L
B
24
3. 非逻辑
当决定某一事件的条件满足时，事 件不发生；反之事件发生
非逻辑真值表
AL
图形符号
0
1
1
0
逻辑表达式 F= A
A
1
L
25
1.3.2 常用复合逻辑运算
与非逻辑运算
或非逻辑运算
L=AB
L=A+B
L
L
与或非逻辑运算 L=AB+CD
L
26
异或运算
AB 00 01 10 11
L 0 1
1 0
逻辑表达式
L=AB=AB+ AB
图A 形符号=1
B
L
同或运算
AB 00 01 10
L 1 0
0
逻辑表达式 L=A B= AB
利用真值表
用真值表证明反演律
A B AB A+ B A• B A+B
00 1
1
1
1
01 1
1
0
0
10 1
1
0
0
11 0
0
0
0
A• B= A+B A+ B=AB
31
1.4.2 逻辑代数中的基本规则
1. 代入规则
任何一个含有某变量的等式，如果等式中 所有出现此变量的位置均代之以一个逻辑函数 式，则此等式依然成立。

逻辑代数基础教程

逻辑代数基础教程

第一章逻辑代数基础教学目标、要求：掌握逻辑函数的四种表示法；掌握逻辑代数的三种基本运算；掌握逻辑代数的公式、基本规则；掌握代数和卡诺图这两种方法化简逻辑函数。

内容提要：常用的数制和码制；基本概念；公式和定理；逻辑函数的化简方法、表示方法及其相互转换。

重点、难点：逻辑运算中的三种基本运算，逻辑函数表示方法及它们之间相互转换；用代数法化简逻辑函数的方法(难点) ；逻辑函数的卡诺图化简法(难点)。

教学方法：启发式、讨论式、探究时，理论、实验和实际应用有机结合。

教学学时：12学时概述一、逻辑代数逻辑代数是反映和处理逻辑关系的数学工具。

逻辑代数是由英国数学家George Bool在19世纪中叶创立的，所以又叫布尔代数。

直到20世纪30年代，美国人Claude E. Shannon在开关电路中找到了它的用途，因此又叫开关代数。

与普通代数相比，逻辑代数属两值函数，即逻辑变量取值只有0、1。

这里的0、1不代表数值大小，仅表示两种逻辑状态（如电平的高低、开关的闭合与断开等）。

逻辑代数中的有些规则和公式与普通代数相同，有些则完全不同。

二、二进制数表示法1．十进制有十个基本数码0、1、2、3、4、5、6、7、8、9，任意数字均由这十个基本数码构成。

逢十进一、借一当十。

同样的数码在不同的数位上代表的数值不同。

任意一个十进制数都可以表示为各个数位上的数码与其对应的权的乘积之和，称权展开式。

如：(209.04)10＝ 2×210＋0×110＋9×010＋0×110-＋4 ×210-2．二进制（1）二进制表示法有两个基本数码0、1 ，任意数字均由这两个基本数码构成。

如1011。

逢二进一、借一当二。

二进制数的权展开式：如：(101.01)2＝ 1×22＋0×12＋1×02＋0×12-＋1 ×22-＝(5.25)10（2）二进制运算运算规则：加法规则：0+0=0，0+1=1，1+0=1，1+1=10 乘法规则：0.0=0， 0.1=0 ，1.0=0，1.1=1二进制加法1101.011+11.11=10001.001二进制减法10001.001-1101.011=11.11二进制乘法11.11×101＝10010.11二进制除法10010.11÷101＝11.113.八进制数有八个基本数码0、1、2、3、4、5、6、7，任意数字均由这八个基本数码构成。

数电第一章逻辑代数基础

数电第一章逻辑代数基础
计数的基数是16，进位规则是“逢十六进一” 任意一个十六进制数D可按“权”展开为：D=ΣkiX16i 如：(2F.8)16=2×161+15×160+8×16-1=(47.5)10 下标16代表十六进制数，有时也用H（Hexadecimal）代
替下标16。
如：2F.8H=47.5D 二进制、十六进制数广泛应用于数字电路
低位
所以：(44.375)10＝(101100.011)2
3.二进制—十六进制转换 十六进制实际上也应属于二进制的范畴 将4位二进制数（恰好有16个状态）看作一个整体时，它的 进位关系正好是“逢十六进一” 所以只要以小数点为界，每4位二进制数为一组（高位不足4 位时，前面补0，低位不足4位时，后面补0），并代之以等值
注意： 不要漏掉 将十进制数展成Σki×2i的形式 0 得到二进制数:knkn-1……k1k0（有小数时还会有k-1……） =1×64+1×32+1×16+1×8+0×4+1×2+1×1 =(1111011)2
例：(123)10=64+32+16+8+0+2+1
或者：采用的方法 — 除2取余、乘2取整 原理：将整数部分和小数部分分别进行转换。 整数部分采用除 2取余法，小数部分采用乘2取整法。转换后再合并。 整数部分采用除2取余法， 先得到的余数为低位，后 得到的余数为高位。
数 字 电 路
车晓镭
第一章 逻辑代数基础
1.1 概述 1.2 逻辑代数的基本运算 1.3 逻辑代数的基本公式和常用公式 1.4 逻辑代数的基本定理 1.5 逻辑函数及其表示方法 1.6 逻辑函数的公式化简 1.7 逻辑函数的卡诺图化简法

第1章 逻辑代数基础(数字电路)

第1章 逻辑代数基础(数字电路)

Ｙ＝Ａ+ Ｙ＝Ａ+Ｂ
19:41
功能表
开关 A 断开 断开 闭合 闭合 开关 B 断开 闭合 断开 闭合 灯Y 灭 亮 亮 亮
真值表
A 0 0 1 1
B 0 1 0 1
逻辑符号
Y 0 1 1 1
实现或逻辑的电 路称为或门。或 门的逻辑符号：
逻辑代数基础
A B
9
≥1
Y=A+B
19:41
3、非逻辑（非运算） 非逻辑（非运算） 非逻辑指的是逻辑的否定。当决定事件 （Y）发生的条件（A）满足时，事件不发 生；条件不满足，事件反而发生。表达式为： Ｙ＝Ａ 开关A控制灯泡Y
数字电子技术基础
逻辑代数基础
1
19:41
•
参考书： 组、阎石，高等教育出版社。
1. 数字电子技术基础，清华大学电子学教研 2. 电子技术基础（数字电路部分），康华光， 高等教育出版社
逻辑代数基础
2
19:41
• 课程要求： 1. 掌握数字电路的基本概念、基本原理、基 本分析方法以及一些典型的电路。 2. 课堂练习与课后练习结合，每周交一次。 3. 进行期中测试，总评成绩：期末60%，期 中20%，作业10%，实验10% 。
逻辑符号
实现与逻辑的电路 称为与门。与门的 逻辑符号：
A
6
&
逻辑代数基础
B
Ｙ＝ＡＢ
19:41
Y
2、或逻辑（或运算） 或逻辑（或运算） 或逻辑的定义：当决定事件（Y）发生的各 种条件（A，B，C，…)中，只要有一个或多个 条件具备，事件（Y）就发生。表达式为： Ｙ＝Ａ＋Ｂ＋Ｃ＋… Ｙ＝Ａ＋Ｂ＋Ｃ＋… 开关A，B并联控制灯泡Y
A

逻辑代数基础知识

逻辑代数基础知识

有1出1，全0出0
非
AY
0 1
有0出1，有1出0
00 ? A0 ? 01 ? A1 ? 11 ? A A ?
A A A ?
00? 01 ? 11 ?
A 0=? A 1=? A A=?
0? 1?
A? A A? A A ?
四种常用逻辑运算：
与非
ABY
00 1 01 1 10 1 11 0
与
ABY
00 0 01 0 10 0 11 1
或
ABY
00 0 01 1 10 1 11 1
非
AY
01 10
2.逻辑表达式
与：Y=A·B 或写成：Y=AB
或： Y=A+B
非: Y A
3.逻辑符号
A
实现与、或、非逻辑运
算的单元电路分别叫做 B
& YA B
≥1 Y A 1
Y
与门、或门、非门
与门
或门
非门
Y ( A B C)( A B) ( A B)( A C)( A B) (B A A)( A C) B( A C)
例3：求 Y AC A(BC) 的反函数。
Y (AC)ABC (AC)A(BC) AC(BC) ABC
注意：
（1）变换前后的运算顺序不变，必要时可以加括 号来保证原来的运算顺序； （2）反演规则中的反变量和原变量的互换只对单 个变量有效。若在“非”号的下面有多个变量， 则在变换时，此“非”号要保持不变，而对“非” 号下面的逻辑表达式使用反演规则。
第一章 逻辑代数基础
1.1 概述 1.2 数制与码制 1.3 逻辑代数 1.4 逻辑函数 课堂练习 课后思考 本章小结
1.3 逻辑代数

第1章 逻辑代数基础

第1章 逻辑代数基础

⑧反演律
A+B= A·B
;
⑨还原律
A== A
AB=A + B
反演律也称德·摩根定理,是一个非常有用的定理.
AB=AC ? A+B=A+C ?
B=C B=C
请注意与普通代数的区别！
三、基本定理
1. 代入定理 任何一个含有变量A的逻辑等式，如果将所有 出现A的位置都代之以同一个逻辑函数F，则等式 仍然成立。 例如：根据 A B = A B
① 0－1律 A ·0=0
;
A+1=1
②自等律
A ·1=A
;
A+0=A
③重迭律
A ·A=A
;
A+A=A
④互补律 A ·A=0
;
A+A=1
⑤交换律
A ·B= B ·A
;
A+B=B+A
⑥结合律 ⑦分配律
A(BC)=(AB)C ; A(B+C)=AB+AC ;
A+(B+C)=(A+B)+C A+BC=(A+B)(A+C)
Y=F(A,B,C,·····)
A
B C
Y
逻辑网络
例如：如图所示是一举重裁判电路，试用逻辑函 数描述逻辑功能。
A为主裁判，B、C
B
A
为副裁判，Y为指
示灯，只有主裁判 和至少一名副裁判
C
Y
认为合格，试举才
算成功，指示灯才
亮
A、B、C： 1 ——认为合格，开关闭合
0 ——不合格，开关断开
Y=F（AY，B，C：）1——试举成功，指示灯亮
0

第一章 逻辑代数基础

第一章 逻辑代数基础
V(v)
t
典型模拟信号
1.1.2 数制和码制 1.1.2数制和码制
一、数制
多位数码中每一位的构成方法以及从低位 到高位的进位规则 • 十进制 Decimal system( 逢十进一） 码：0，1，2，3，4，5，6，7，8，9 基：10 权： 10i i D = k × 10 表达式： ∑i
(143.75)10 = 1×10 2 + 4 ×101 + 3 ×100 + 7 ×10 −1 + 5 ×10−2
1 = 0， 0 =1
1+A=1 0+A=A A+A=A A+ Ā=1 A+B=B+A A+(B+C)=(A+B)+C A+B •C=(A+B) •(A+C) 重叠律 互补律 交换律 结合律 分配律 反演律 还原律
A⋅ B = A+ B
A + B = A⋅ B
1.3.2若干常用公式
序号 21 22 23 24 25 26 公式 A + A·B = A A + Ā·B = A + B
A B
Y
0 1 1 1
�Y
E
0 0 1 1
0 1 0 1
或逻辑表达式为： Y=A+B A 或运算由与逻辑门电路实现，其逻辑符号为： B
≥1
Y
• 非运算：只要条件具备了，结果就不会发生；而条
件不具备时；结果就发生。 例：设1表示开关闭合或灯亮；0表示开关不闭合或灯不亮
R A Y A
�Y
0 1 1 0
编码种类 十进制数 0 1 2 3 4 5 6 7 8 9 权 8421码 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 8421 余3码 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 2421码 0000 0001 0010 0011 0100 1011 1100 1101 1110 1111 2421 5211码 0000 0001 0100 0101 0111 1000 1001 1100 1101 1111 5211 余3循环码 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第一章逻辑代数基础
一、简答题：
1、什么叫做算术运算，什么叫做逻辑运算？
答：当两个二进制数码表示数量大小时，它们之间进行的数值运算，称之为算术运算；
当两个二进制数码表示不同的逻辑状态时，它们之间可以按照指定的某种因果关系进行的运算，称之为逻辑运算。

2 逻辑代数中三种最基本的逻辑运算是什么？各遵循什么运算关系？
答：分别为与运算、或运算和非运算。

与逻辑的定义：仅当决定事件（Y）发生的所有条件（A，B，C，…）均满足
时，事件（Y）才能发生。

表达式为：Y=ABC……
或逻辑的定义：当决定事件（Y）发生的各种条件（A，B，C，…)中，只要
有一个或多个条件具备，事件（Y）就发生。

表达式为：
Y=A+B+C+……
非逻辑：决定事件发生的条件只有一个，条件不具备时事件发生（成立），条
件具备时事件不发生。

表达式为：A
Y
3 逻辑函数的五种表示方法是什么？各有什么特点？
答：分别为真值表、逻辑表达式、卡诺图、逻辑图、波形图。

4 什么叫最小项？最小项有什么性质？
答：定义：对于n个变量，如果P是一个含有n个因子的乘积项，而且每一个变量都以原变量或者反变量的形式，作为一个因子在P中出现且仅出现一次，那么就
称P是这n个变量的一个最小项。

性质：（1）每一个最小项都有一组也只有一组使其值为1的对应变量取值；
（2）任意两个不同的最小项之积恒为0；
（3）全部最小项之和恒为1。

5 卡诺图 中合并最小项的规则是什么？
答：合并逻辑相邻项。

（1）相邻单元的个数是2n
个，并组成矩形时，可以合并。

（2）卡诺圈尽可能大：利用吸收规则， 2n 个相邻单元合并，可吸收掉n 个变量。

（3）不要圈出多余圈：各最小项可以重复使用，但每一次新的组合，至少包含一个
未使用过的项，直到所有为1的项都被使用后化简工作方算完成。

（4）注意边沿和四角。

（5）如果是具有约束的逻辑函数，要注意利用约束项，可以使结果大大简化。

二、化简逻辑函数
1、将下列逻辑表达式化成最简与-或式。

（1）B AD CD B A Y ⋅+++= （2）A D DCE B D B A Y +++=
（3）C B C A C B C A Y +++= （4）B)CD A (B A Y ++=
解：（1）B AD CD B A Y ⋅+++=
B
A B C D )(B AD)(A B
AD BCD A +=+++=+++=
（2）A D DCE B D B A Y +++=
DCE )A D(B B A +++=
DCE A B D B A ++= （摩根定理）
DCE D B A ++=D B A += （吸收定理）
（3）C B C A C B C A Y +++=
C
B B A
C A C B C A C B B A C A B
A C
B
C A C B C A ++=++++=++++=
（4）B)CD A (B A Y ++=
CD B A CD
B A B A CD
B)A (B A +=∙+=++=
2、用卡诺图化简下列函数。

（1）Y=∑m （0，2，3，5，6，8，9，10，11，12，13，14，15）
（2）C B C A B A D B B C D C A Y ∙+++++∙=
（2）C B C A B A D B B C D C A Y ∙+++++∙=
解：（1）Y=∑m （0，2，3，5，6，8，9，10，11，12，13，14，15）
所得最简表达式为：D C B D B C B D C A Y +⋅+++=
（2）C B C A B A D B B C D C A Y ∙+++++∙=
所得最简表达式为：C
+
Y+
=
B
D
A
3、用卡诺图化简具有约束的逻辑函数）
m
3
）
2
1
F∑
4
=，约束条
A,
B,
C,
D
（
，
，
，
，
，
5
，
6
8
（9
，
，
件：AB+AC＝0。

解：）
，
1
2
3
D）
C,
=，约束条件：AB+AC＝0。

所得最简表达F∑
A,
B,
4
m
，
，
，
，
5
，
，
6
，
8
（9
（
式为：D
Y约束条件：AB+AC＝0。

=B
+
C+
三、分析题：
1、将下列各数转换成二进制数，并写出其奇、偶校验码。

（1）（21）10；（2）（45）10；（3）（65）10；
解：（1）（21）10＝（10101）2；奇：101010，偶：101011
（2）（45）10＝（101101）2；奇：1011011，偶：1011010
（3）（65）10＝（1000001）2；奇：10000010，偶：10000011。