当前位置：文档之家 › 大学物理一复习第四章刚体的转动共52页文档

大学物理一复习第四章刚体的转动共52页文档

  • 格式：ppt
  • 大小：1.09 MB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

大学物理第四章刚体转动

大学物理第四章刚体转动

进动和章动在自然界中实例
陀螺仪
地球极移
陀螺仪的工作原理即为进动现象。当 陀螺仪受到外力矩作用时，其自转轴 将绕某固定点作进动，通过测量进动 的角速度可以得知外力矩的大小和方 向。
地球极移是指地球自转轴在地球表面 上的移动现象，其产生原因与章动现 象类似。地球极移的周期约为18.6年 ，且极移的幅度会受到地球内部和外 部因素的影响。
天体运动
许多天体的运动都涉及到进动和章动 现象。例如，月球绕地球运动时，其 自转轴会发生进动，导致月球表面的 某些特征（如月海）在地球上观察时 会发生周期性的变化。同时，行星绕 太阳运动时也会发生章动现象，导致 行星的自转轴在空间中的指向发生变 化。
感谢观看
THANKS
02
刚体定轴转动动力学
转动惯量定义及计算
转动惯量定义
刚体绕定轴转动时，其惯性大小的量度称为转动惯量，用字母$J$表示。它是一个与刚体质量分布和转轴位置有 关的物理量。
转动惯量计算
对于形状规则的均质刚体，可以直接套用公式计算其转动惯量；对于形状不规则的刚体，则需要采用间接方法， 如分割法、填补法等，将其转化为规则形状进行计算。
刚体性质
刚体是一个理想模型，它在力的作用 下，只会发生平动和转动，不会发生 形变。
转动运动描述方式
01
02
03
定轴转动
平面平行运动
ห้องสมุดไป่ตู้
定点转动
物体绕一固定直线（轴）作转动。
物体上各点都绕同一固定直线作 不同半径的圆周运动，同时物体 又沿该固定直线作平动。
物体绕一固定点作转动。此时物 体上各点的运动轨迹都是绕该固 定点的圆周。
非惯性系下刚体转动描述方法
欧拉角描述法

大学物理—刚体的动轴转动

大学物理—刚体的动轴转动
（3）J 和质量分布有关； （4）J 和转轴有关，同一个物体对不同转轴的转 动惯量不同。 例 1: 一轻绳跨过一定滑轮，滑轮视为圆盘，绳 的两端分别悬有质量为m1和m2的物体1和2，m1< m2 如图所示。设滑轮的质量为 m ，半径为 r ，所受的 摩擦阻力矩为 m 。绳与滑轮之间无相对滑动。试求 物体的加速度和绳的张力。 解:滑轮具有一定的转动惯量。在转动中受到 阻力矩的作用，两边的张力不再相等，设物体1这 边绳的张力为T1、 T1’(T1’= T1) ，
F r sin f r sin (m r
i 1 i i i i 1 i i i i 1
N
N
N
N
2
i i
)
根据内力性质(每一对内力等值、反向、共 线,对同一轴力矩之代数和为零)，得：
f r sin
i 1 i i
i
0
得到：
F r sin (m r
1
麦克斯韦分布
所以刚体内任何一个质点的运动，都可代表整个 刚体的运动。 刚体运动时，如果刚体的各个质点在运动中 都绕同一直线圆周运动，这种运动就叫做转动， 这一直线就叫做转轴。 3. 刚体的定轴转动 定轴转动： 刚体上各点都绕同一转轴作不同半径的圆周运 动，且在相同时间内转过相同的角度。 特点： (1) 角位移，角速度和角加速度均相同；
Lz Li cos mi Ri v i cos mi ri v i
m r
2 i i
10
式中 mi ri2 叫做刚体对 Oz 轴的转动惯量， 用J表示。
麦克斯韦分布
刚体转动惯量：
J mi ri2
刚体绕定轴的角动量表达式：
Lz J

大学物理学 第4章刚体力学

大学物理学 第4章刚体力学
第四章 4.1 刚体运动学
4.1.1 刚体：
刚体力学
在外力作用下，形状和大小都不发生变化的物体 .
4.1.2 刚体的基本运动形式： （1）平动：若刚体中所有点的 运动轨迹都保持完全相同，或者 说刚体内任意两点间的连线在各 时刻总是平行. 刚体平动 质点运动
（2）转动： 定轴转动、定点转动 定轴转动: 转轴在所选参考系中固定不动的转动
(2) 由转动定律求 ，(唱片J=mR2/2)
M 4 g J 3R
2 M Rmg 3
由 0 t 可求得
2 2 0
3R t 4 g
(3) 由 2 可得在 0 到 t 2 3 R 的时间内，转过的角度为
8g
1 2 2 驱动力矩做的功为 W M mR 4
m 2 Tr T1r r 2 m 2 T2 r Tr r 2 a r
mg
2m g
解出
11 T mg 8
例：已知杆质量 m，长l，绕一端点转动， 1 2 J ml ，初水平静止，求位于任意 3
N
n
)
受力：轴支持力 N、重力mg
角时，、为多少？
J r 2 dm
r
dm
o
例1 计算质量为m，长为l 的细棒绕一端的转动惯量。 z 1 2 解： J r 2dm J o ml 3 dm m o O dm dx dx x l x dx
r 2 x2 l ml 0 0 l 3 l 3
角时机械能
t

mg
由机械能守恒可求得
J 2 l mg sin 0 2 2
3g sin l
d 3g d cos dt l dt

【精选】大学物理一复习 第四章 刚体的转动

【精选】大学物理一复习 第四章 刚体的转动

m
轮子的转动惯量 J。
h
P144作业 ４-11
受力分析：
m：mg T ma
(1)
M：TR J
(2)
物体从静止下落时满足
h at 2/2
(3)
a R
(4)
J mR 2 ( gt 2 2h ) 2h
M ,R
T
T
h
mg
书例3 一长为 l 、质量
为 m 匀质细杆竖直放置， 其下端与一固定铰链O相 接，并可绕其转动．由于 此竖直放置的细杆处于非
如令 mC 0，可得：
T1
T2
mAmB g mA mB
2）物体B 由静止出发作匀加速直线运动
v2 v02 2as
第二类问题：已知运动情况和力矩M ，求 J。
例：测轮子的转动惯量用一 M , R
根轻绳缠绕在半径为 R、质
量为 M 的轮子上若干圈后，
一端挂一质量为 m 的物体，
从静止下落 h 用了时间 t ,求
第一类问题：已知J和力矩M ：求 和以及F。
书例2 质量为mA的物体A 静止在光滑水平面 上，和一质量不计的绳索相连接，绳索跨过一
半径R、质量mC的圆柱形滑轮C，并系在另一质 量为mB 物体B上，B 竖直悬挂．滑轮与绳索间 无滑动， 滑轮与轴承间的摩擦力可略去不计．
(1)两物体的线加速度为多少？ 水平和竖直两
段绳索的张力各为多少？
A
(2) 物体 B 从静止落下
mA
C
mC
距离 y 时，其速率是多少？
mB B
解：隔离法，受力分析
A
分别根据牛二定律和转动定律列方程：
角量、线量关系式
解得：
a
mB g

大学物理—刚体的动轴转动

大学物理—刚体的动轴转动

25
麦克斯韦分布
2 1 2 d mgR J mR 3 2 dt
设圆盘经过时间t停止转动，则有
t 0 2 1 g dt R d 0 0 3 2
F1
转动 平面
F
F2
r F1 只能引起轴的
变形, 对转动无贡献。 注 （1）在定轴动问题 中，如不加说明，所指的 力矩是指力在转动平面内 的分力对转轴的力矩。
r
（2） M Z rF2 sin F2d
d r sin 是转轴到力作
用线的距离，称为力臂。
F123麦克来自韦分布例 2: 一半径为 R ，质量为 m 匀质圆盘，平放 在粗糙的水平桌面上。设盘与桌面间摩擦系数为 ，令圆盘最初以角速度 0 绕通过中心且垂直盘 面的轴旋转，问它经过多少时间才停止转动？

d r dr
R
e
解 : 因摩擦力不是集中作用于一点，而是分布 在整个圆盘与桌子的接触面上，力矩的计算要用积 分法。在图中，把圆盘分成许多环形质元，每个质 元的质量dm=rddre，所受到的阻力矩是rdmg 。
a m2 G2
a
21
式中是滑轮的角加速度，a是物体的加速度。滑轮 边缘上的切向加速度和物体的加速度相等，即
麦克斯韦分布
a r
从以上各式即可解得
m 2 m1 g M r / r m 2 m1 g M / r a
J m 2 m1 2 r 1 m 2 m1 m 2
1. 刚体的角动量
图为以角速度绕定轴oz 转动的一根均匀细棒。
L
z

ri
O
Li
把细棒分成许多质点，其中第 i 个质点的质量为 mi 当细棒以转动时，该 质点绕轴的半径为 ri

大学物理一复习第四章刚体的转动-文档资料

大学物理一复习第四章刚体的转动-文档资料

mg FT2 ma2

FT1 FT2
R
mg FT1 r
m
a1
J
a1 r
a2 R
FT1 r R
FT1'
A
mg
β
FT2
FT2'
B
mg
mg(R r)
J mR2 mr2
a1

r

J
mgr(R r) mR2 mr2
40 半径减小角速度增加。
（2）拉力作功。请考虑合外力矩为0， 为什么拉力还作功呢？
W


0
Md
在定义力矩作功 时，我们认为只 有切向力作功， 而法向力与位移 垂直不作功。
但在例题中，小 球受的拉力与位 移并不垂直，小 球的运动轨迹为 螺旋线，法向力 要作功。
o
F
r d Fn F
解得
a2

R

mgR(R r) J mR2 mr2
FT1 mg ma1
FT2 mg ma2
例2：光滑斜面倾角为 ，顶端固定一半 径为 R ，质量为 M 的定滑轮，质量为 m 的物体用一轻绳缠在定滑轮上沿斜面 下滑，求:下滑的加速度 a 。
解：物体系中先以
物体 m 研究对象，
A
分别根据牛二定律和转动定律列方程：
角量、线量关系式
解得：
a
mB g
mA mB mC 2
T1

mAmB g
mA mB mC
2
T2

(mA mC 2)mBg mA mB mC 2
如令 mC 0，可得：

大学物理-刚体的转动

大学物理-刚体的转动
刚体内所作的任何一条直线，始终保持和自 身平行的运动。平动时，刚体上各点的运动轨迹都 相同，因此，刚体上一点的运动可代表整个刚体的 运动。 ( 刚体平动的运动规律与质点的运动规律相 同）

3、刚体绕定轴转动：
rotation of a rigid body around a
z
fix axis 转轴相对于参照系不动的转动称为定轴转动。
z or
1、力矩的功： work done by torque
Fi 表示作用在刚体上P点的 外力，当物体绕轴有一角位移 d 时，力 Fi 做的元功为
d
ds
i Fi
i
P
dAi F i d r Fi cos d r Fi cos ds Fi ri cos d
因为 cos sin i
设刚体中第i个质点的质量为 mi ，速度为 vi ， 则该质点的动能是 1 1 2 Eik mi vi mi (ri ) 2 2 2 整个刚体的动能 1 1 2 Ek mi vi ( mi ri 2 ) 2 2 2
2 m r 式中 i i 正是刚体对转轴的转动惯量J
2
a
( m 2 m1 ) g
Mr
m1 m 2 J
r
( m 2 m1 ) g
Mr
当不计滑轮质量 及摩擦阻力即令
r
m0
T1 T2
Mr 0
2m1m2 g m1 m2
1 M m 2 ( 2 m1 m ) g r r 2 T2 m 2 ( g a ) 1 m1 m 2 m 2
刚体的转动动能
1 Ek J 2 2
3、刚体的转动惯量 rotational inertia (moment of inertia)

大学物理-ch4_刚体的转动汇总

大学物理-ch4_刚体的转动汇总

J
dJ
2m R2
R 0
r 3dr
1 2
mR2
m
R 2
J
常 见 刚 体 的 转 动 惯 量
三、 力矩
使物体转动，必须给定一 个作用力，另外考虑转动与力 的作用点以及作用力的方向有 关，因此在研究物体转动中引
（入1力）矩若这刚一体物所理受量力。F在转动平面内
z
Od
r
F
F
P
力臂：rsin = d 表示转轴到力作用线的垂直距离。
（2）转动惯量J的大小决定于
刚体的质量：同形状的刚体，ρ(λ,σ)越大，J 就越大 质量的分布：质量相同，dm 分布在 r 越大的地方，则 J越大 刚体的转轴位置：同一刚体依不同的转轴而有不同的J
（3）转轴相同的刚体系统的总转动惯量等于各刚体转动
惯量的代数和
J J1 J2 Jn
转动惯量的计算：
c
2
t2
2 600π 3002
π 75
rad s3
1 ct 2 π t 2
2 150
由 d π t 2
dt 150
得
d
π
t t 2dt
0
150 0
π t 3 rad
450
在 300 s 内转子转过的转数
N π (300)3 3104
2π 2π 450
例 一条缆索绕过一定滑轮拉动一升降机，滑轮半
向转动，则力矩Mz为正，反之为Mz为负。
力矩
M
r
F
M
ห้องสมุดไป่ตู้
F
方向：满足右手螺旋法则 对于定轴转动，力矩的方向沿 转轴方向，但只有两种可能， 则可用正负表示
即：力矩与坐标轴同向时为正 ，反向时为负

大学物理第四章 刚体的转动(3课时)讲解

大学物理第四章 刚体的转动(3课时)讲解

c

2
t2

2 600π 3002

π 75
rad s3
1 ct 2 π t 2
2 150
4-1 刚体的定轴转动
由 dq π t 2
dt 150
得
q
dq
π
t t 2dt
0
150 0
q π t 3 rad
450
在 300 s 内转子转过的转数
N q π (300)3 3104
第四章 刚体的转动
物理学
第五版
4-0 教学基本要求
四 理解刚体定轴转动的转动动能概 念，能在有刚体绕定轴转动的问题中正确 地应用机械能守恒定律．
能运用以上规律分析和解决包括质点 和刚体的简单系统的力学问题．
第四章 刚体的转动
物理学
第五版
第一节
第四章 刚体的转动
4-1 刚体的定轴转动
刚体：在外力作用下，形状和大小都不 发生变化的物体．(任意两质点间距离保持 不变的特殊质点组．)
18 000 r·min-1 ．转子的角加速度与时间成正
比．问在这段时间内，转子转过多少转？
解 令 ct，即 d ct ，积分
dt

t
d c tdt
得 1 ct 2
0
0
2
4-1 刚体的定轴转动
1 ct 2
2
当 t =300 s 时
18 000 r min 1 600 π rad s1
位置及方向 不变。
பைடு நூலகம்
该平面且通 过质心
刚体上 各质点都 以某一定 点为球心 的各个球 面上运动
复杂 的运动 与平动 的混合。

大学物理 第四章 刚体的转动 4-4 力矩的功 刚体绕定轴转动的动能定理

大学物理 第四章 刚体的转动 4-4 力矩的功 刚体绕定轴转动的动能定理
第四章 刚体的转动
6

物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理 -
W =∫
外力的功
θ2
θ1
1 1 2 2 M d θ = Jω 2 − Jω 1 2 2
刚体动能的改变 质点系的动能 定理在刚体中 的具体表现
刚体作为特殊的质点系， 刚体作为特殊的质点系， 满足质点系的动能定理： 满足质点系的动能定理：
方向： 方向：
dM
刚体的转动
14
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理 -
2 µ mg 2 dM = r dr 2 R
整个唱片所受的摩 擦力矩为
R
v df
o
r
dl dr
M = ∫ dM
方向： 方向：
dM
M
2 µmg M = 2 R
∫
R
0
2 r dr = µRmg 3
2
刚体的转动
第四章
非保守内力： 非保守内力：刚体内力 W
m v v
in 刚体
=0
∴W
ex
+W
in nc
=0
18
E = E0
第四章 刚体的转动
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理 -
o
选初始位置为势能零点
30
o
a
1 1 2 2 2 ( m′l + ma )ω = 2 3
o
m v v
'
l ′g (1 − cos 30o ) mga(1 − cos 30 ) + m 2
v dr φ
o
刚体的转动

大学物理学(上册)第4章 刚体的转动_OK

大学物理学(上册)第4章 刚体的转动_OK

系统，其所受外力是两者的重力以及轴处轴对
l
杆的支持力，所有这些外力对轴的力矩为零，
因此系统对轴的角动量守恒.
m1
m10l
m11l
1 3
m2l 2
3m1(0 1) 25rad s-1
m2l
24
变为 ω2 ，积分可得：
t2 t1
Mdt
J2
J1
角动量定理积分形式
21
4.4.3 角动量守恒定律
定轴转动的角动量定理
M
dL dt
若 M 0 ， L 常矢量
对于某一固定轴，当刚体所受合外力矩为零时，其角动量 保持不变。(惯性系)-----角动量守恒定律
讨论
守恒条件 M 0
若 J不变， 不变；
若 J 变， 也变，但
L J 不变.
22
内力矩不改变系统的角动量.
在冲击等问题中 M内 M外 L 常量
角动量守恒定律是自然界的一个基本定律.
自然界中存在多种守恒定律
动量守恒定律 能量守恒定律 角动量守恒定律
电荷守恒定律 质量守恒定律 宇称守恒定律等
23
例1 如图所示，一竖直悬挂的木杆，可绕杆端O处的水平
动惯量为Jz，轴与平面的交点为O，物体绕平面内通过0点 相互垂直的两轴的转动惯量分别为Jx和Jy，则有：
Z
Jz Jx Jy
XO Y
o
o´
实心圆盘
16
例1. 求质量为m，长度为 L 的均质细棒的转动惯量。（转轴
oo´通过棒的一端并与棒垂直） 0
L
解：在距转轴x处，取质量元dm，
其长度为dx
0
x dx dm
J miri2 m1r12 m2r22 m3r32 i 1

大学物理B(上)第4章 刚体的转动

大学物理B(上)第4章 刚体的转动

度 0 0，经300s 后，其转速达到 18000r·min-1 . 已知转
子的角加速度与时间成正比 . 问在这段时间内，转子转
过多少转？
（变角加速转动）
解:(1) 先求 ~ t 关系 由题意，令 ct，即 d ct，积分
dt

t
d c tdt
得 1 ct 2
z
r 刚体内任意一质元到转轴的垂直距离 i
v
转 ri P
动 平
θ
参
面
考
方
θ
向
线速度 i ri 切向加速度 ait ri
法向加速度 ain ri 2
ω
ω
定轴转动时，刚体上任意质元作圆周运动具有相同的，，
即定轴转动用角量描述最为方便。
4一– 1 刚刚体体的转定动轴的转角动速度和角加速度第四章 刚体的转动
4 – 1 刚体的定轴转动
第四章 刚体的转动
§4.1 刚体的基本运动(2)
4刚–体1 ：刚在体外的力定作轴用转下动，形状和大小都不第发四生章变刚化体的的物转体动 . （任意两质点间距离保持不变的特殊质点组） 刚体的运动形式：平动、转动 .
一. 平动
GTPD
刚体中所有点的运动轨迹都保持完全相同，或者说刚体内任 意两点间的连线总是平行于它们的初始位置间的连线 .
4例–11 刚一飞体轮的半定径轴为转动0.2m、 转速为150r第·m四in章-1，刚因体受的转制动 动而均匀减速，经 30 s 停止转动 . 试求：
(1)角加速度和在此时间内飞轮所转的圈数；
(2)制动开始后 t = 6 s 时飞轮的角速度；
(3)t = 6 s 时飞轮边缘上一点的线速度、切向加速度和法向加速度 .

大学物理第四章 刚体的转动_4-2

大学物理第四章 刚体的转动_4-2

例1：长为 l、质量
为 m 的细杆，初始
时的角速度为 0，
ol
由于细杆与桌面的
摩擦，经过时间 t
后杆静止，求摩擦 力矩 M阻。
4 – 2 力矩 转动定律 转动惯量
第四章 刚体的转动
解：以细杆为研究对象，只有摩擦阻力产生力矩，由 匀变速转动公式：
0 t
0 t 0
ol
0
t
细杆绕一端的转动惯量 J 1 ml 2
1 mgl sin J
2
4 – 2 力矩 转动定律 转动惯量
第四章 刚体的转动
1 mgl sin J
2 式中 J 1 ml2
3
得 3g sin
2l
由角加速度的定义
d d d d dt d dt d
d 3g sind
2l
代入初始条件积分 得
3g (1 cos )
l
4 – 2 力矩 转动定律 转动惯量
F
Fi 0 , Mi 0
4 – 2 力矩 转动定律 转动惯量 讨论
第四章 刚体的转动
1）若力 F 不在转动平面内，把力分解为平行和垂
直于转轴方向的两个 分量
F Fz F
其中 Fz 对转轴的力
矩为零，故 F 对转轴的
力矩 M zk r F
z
k
Fz
F
O r
F
M z rF sin
例5 一长为 l 质量为 m 匀质细杆竖直放置，其
下端与一固定铰链 O 相接，并可绕其转动 . 由于此
竖直放置的细杆处于非稳定平衡状态，当其受到微小 扰动时，细杆将在重力作用下由静止开始绕铰链O 转
动 .试计算细杆转动到与竖直线成 角时的角加速度
和角速度 .

第4章刚体转动-精选

第4章刚体转动-精选

对质量连续分布的刚体
∑
所有质点都以其垂轴 距离为半径作圆周运动
2019/11/17
35
长江大学物理教程
刚体的角动量定理
质点的角动量定理
（微分形式） （积分形式）
1.刚体的
合外力矩
冲量矩
2019/11/17
（微分形式）
角动量的时间变化率
（积分形式）
角动量的增量
36
长江大学物理教程
（微分形式） （积分形式）
刚体平动 质点运动
刚体平动的运动规律与质点的运动规律相同。
2019/11/17
7
长江大学物理教程
转动：分定轴转动和非定轴转动
刚体的平面运动
2019/11/17
8
长江大学物理教程
刚体的一般运动可看作：
随质心的平动 + 绕质心的转动 的合成
2019/11/17
9
长江大学物理教程
定轴转动参量
1. 角位置
解 细杆受重力和 铰链对细杆的约束力FN
作用，由转动定律得
1mgslinq J
2

m,l FN
θ mg
O
式中 J 1 ml 2 3
得 3g sinq
2l
2019/11/17
31
长江大学物理教程
由角加速度的定义
dωdωdθ ω d ω

m,l FN
dt dθ dt d θ
∑
∑
∑
是矢量式
与质点平动对比
2019/11/17
37
长江大学物理教程
3 刚体定轴转动的角动量守恒定律 由
若
刚体所受合外力矩
则
即

大学物理刚体的转动

大学物理刚体的转动
公式表示
$Delta E_{k} = int_{t_{1}}^{t_{2}} vec{M} cdot mathrm{d}vec{θ}$，其中$vec{M}$为合外力矩， $mathrm{d}vec{θ}$为刚体的角位移。
动能与转动惯量的关系
动能与转动惯量的关系
刚体的转动动能等于转动惯量与角速度平方的乘积的一半，即$E_{k} = frac{1}{2} I omega^{2}$，其中$I$为转动惯量，$omega$为角速度。
THANKS.
实验步骤与操作
准备实验设备和材料，检查刚体 转动装置是否稳固。
将刚体用细线悬挂于转动轴上， 调整砝码的位置，使刚体平衡。
使用测角仪测量刚体的初始角度， 记录数据。
实验步骤与操作
01
释放刚体，开始计时， 同时观察刚体的转动情 况，记录数据。
02
使用天平测量砝码的质 量，计算刚体的转动惯 量。
03
根据实验数据，计算刚 体的角速度、角加速度 等物理量。
物理意义
根据刚体的质量和形状，通过计算其 相对于某固定轴的惯性矩来确定。
反映了刚体绕固定轴转动的惯性大小。
影响因素
刚体的质量分布和形状，以及转动轴 的位置。
转动定律的应用
陀螺仪
利用角动量守恒原理制作 的陀螺仪，可以用来测量 角度和方向。
自行车轮
自行车轮在行驶过程中， 由于角动量守恒，可以通 过调整车轮的转动惯量来 改变行驶稳定性。
03
题的能力。
刚体的基本概念
02
刚体的定义
刚体：在任何力的作用下，大 小和形状保持不变，只发生刚 性变形的物体。
刚体是一个理想化的物理模型， 用于简化对实际物体运动的研 究。
刚体在现实世界中并不存在， 但可以近似地描述一些物体在 一定条件下的运动特性。

大学物理学 刚体的转动.

大学物理学 刚体的转动.

an
r
a
e v
a r a n r 2
a r e r 2 e n
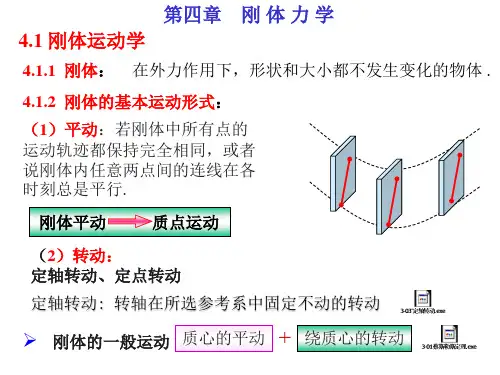
例 一匀质细棒可绕通过第其四一章端刚的体固的定转动的 水平轴O转动，如图，当细棒与水平线夹角为θ时， 其角加速度 ＝3gcos,l为棒长求。它自静止
2l
1＝3开始摆2＝ 到2时的角速度，并求
A和B点的线速度的大小。
解：＝ d 3gco sd O θ
：质量面密度
对质量体分布的刚体：dmdV
：质量体密度
第四章 刚体的转动 关于刚体对轴的转动惯量，下列说法中正确的是
（Ａ）只取决于刚体的质量，与质量的空间分布 和轴的位置无关．
（Ｂ）取决于刚体的质量和质量的空间分布，与 轴的位置无关．
（Ｃ）取决于刚体的质量、质量的空间分布和轴 的位置．
（Ｄ）只取决于转轴的位置，与刚体的质量和质 量的空间分布无关．
第四章 刚体的转动
1）若力 F不在转动平面内，把力分解为平行和垂
直于转轴方向 的两个分量
F F zF
其中 Fz 对转轴的力
矩为零，故 F对转轴的 力矩 M zk ˆ rF
z
k
Fz
F
O r F
M zr F sin
2）合力矩 等于各 分力 矩的矢 量和 M M 1 M 2 M 3
第四章 刚体的转动
3） 刚体内作用力和反作用力的力矩互相抵消
Mij
O
rj
dri
j
i Fji
Fij
Mji
M ijM ji
第四章 刚体的转动
有两个力作用在一个有固定轴的刚体上. (1)这两个力都平行于轴作用时,它们对轴的合力矩一定是零; (2)这两个力都垂直于轴作用时,它们对轴的合力矩可能是零; (3)这两个力的合力为零时,它们对轴的合力矩也一定是零; (4)当这两个力对轴的合力矩为零时,它们的合力也一定是零. 在上述说法中, (A)只有(1)是正确的. (B) (1)、(2) 正确, (3)、(4)错误, (C) (1)、(2)、(3)都正确, (4)错误. (D) (1)、(2)、(3)、(4)都正确.

大学物理：Cha.4 刚体定轴转动

大学物理：Cha.4 刚体定轴转动
每学期、每章首页
上次课的主要内容
第四章 刚体的定轴转动
本章内容、重点、难点
第一节
一、刚体
刚体的基本运动--平动
二、刚体的基本运动
+ 刚体的运动 质心的平动 平动加转动
绕质心的转动
➢ 刚体的平面运动 .
+ 刚体的运动
质心的平动 （续）平动加转动
绕质心的转动
（续）二、基本运动--平动
转动与碰撞
（续）转动与碰撞
例
木棒 子弹
联立解得
例
以弹、棒为系统 击入阶段 子弹击入木棒瞬间，系统在
竖直位置，受合外力矩为零，角动量守恒。 该瞬间之始 该瞬间之末
弹
棒弹
棒
上摆阶段 弹嵌定于棒内与棒一起上摆，
用系统动能定理，其中非保守内力的功为零，
外力（重 上摆末动能
力）的功
上摆初动能
外
其中
例
（续）刚体定轴转动定律
定律应用的注意
两个常用的转动惯量
例
细绳缠绕轮缘
初 始 静 止
轮轴无摩擦 轻绳不伸长 轮绳不打滑
变力
制动前
例
0. 5
2
制动的 阻力矩
制动过程使得
降至 0.5 时的
需时
0.5
0.5
0.693
0.693
例
例
（续）例
匀直细杆一端为 轴水平静止释放
例
由 求 本题
力臂
代入得：
11.2 km/s > v1 > 7.9 km/s
椭圆
v1 = 7.9 km/s
圆
v1
远地点
v2
近地点
卫星 的角动量对地心 守恒

大学物理 第四章 刚体的转动 4-2 力矩 转动定律 转动惯量

大学物理 第四章 刚体的转动 4-2 力矩 转动定律 转动惯量

} ⇒ω
} ⇒θ
2、 M = Jα
F = ma
}⇒
17
m反映质点的平动惯性，J 反映刚体的转动惯性。 反映质点的平动惯性， 反映刚体的转动惯性。 反映质点的平动惯性
三 转动惯量
J 的计算方法 质量离散分布
J = ∑ ∆m r
j
2 j j
J = ∑ ∆m r = (∆m )r + (∆m2 )r + L+ (∆mN )r
质量为m，长为L的细棒绕其一端的 的细棒绕其一端的J 质量为 ，长为 的细棒绕其一端的
1 2 J c = mL 12
O1
O1’
L2 1 2 J = J c + m( ) = mL 2 3
d=L/2
O2 O2’
20
竿 子 长 些 还 是 短 些 较 安 全 ？
飞轮的质量为什么 大都分布于外轮缘？ 大都分布于外轮缘？
（3） ）
1 2 对M： T2 r − T1r = J α = M r α ： 2
4、运动学： 运动学：
rα = a
（4） ）
26
解以上四个联立方程式, 解以上四个联立方程式 可得
1 T2 ' ≠ T 、
原因： 原因：
' 1
' (1)若：T2 ' = T T2 ' r −T ' r = Jα v 1 1 FN v 1 T 1 ⇒ J = mr2 = 0 ⇒m = 0 2 m
21
例1（补充例题）：一个转动惯量为2.5 kg⋅m2 、 （补充例题） 一个转动惯量为 ⋅ 例题 直径为60cm 的飞轮，正以 的飞轮，正以130 rad⋅s−1 的角速度旋转。 直径为 ⋅ 的角速度旋转。 现用闸瓦将其制动, 现用闸瓦将其制动 如果闸瓦对飞轮的正压力为 500 N, 闸瓦与飞轮之间的摩擦系数为0.50。求： 闸瓦与飞轮之间的摩擦系数为 。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4、角动量守恒定律 条件：M=0
熟练掌握
1 如图：一定滑轮两端分别悬挂质量 都是m的物块A和B，图中R和r，已知滑轮 的转动惯量为J，求A、B两物体的加速度及 滑轮的角加速度．
熟练掌握
ω d
dt
dω dt
d2
d2t
v rωe t
at r
an rω 2
an r a
et at v
a re trω 2e n
§4-2 力矩 转动定律 转动惯量
一、力矩
M r F
z
F
M Fsrin Fd O M drP*
M 的方向由右手法则确定
掌握
➢力矩的方向 对于定轴转动可用正、负号表示。
z
讨论
O
y
掌握
B
1） 是矢量、状态量 方向：右手定则确定
xA
大小：
2）角动量与参考点的选取有关
o
m
m
o
o
m
掌握
2、质点的角动量守恒定理
守恒条件：
(1) (2)
熟练掌握
例：彗星绕太阳作椭圆
r
轨道运动，太阳位于椭
圆轨道的一个焦点上，
问系统的角动量是否守
恒？近日点与远日点的
速度谁大？
二、刚体定轴转动的角动量定理及守恒定律
m,l
θ mg
O
稳定平衡状态，当其受到微小扰动时，细
杆将在重力作用下由静止开始绕铰链O 转
动．试计算细杆转动到与竖直线成角时
的角加速度和角速度．
解 细杆受重力和
铰链对细杆的约束力FN
作用，由转动定律得
M1mgslinJ
2
m,l
FN
θ
mg O
式中 J 1 ml 2 3
得 3g sin
2l
由角加速度的定义
（A）2 v 3L
（C）6 v 7L
4v （B）5 L
（D）8 v 9L
mv v om o
例2：如图所示，一静止的均匀细棒，长为L、
质量为M，可绕通过棒的端点且垂直于棒长
的光滑固定轴O在水平面内转动，转动惯量
为．一质量为m、速率为v的子弹在水平面内
沿与棒垂直的方向射出并穿出棒的自由端，
设穿过棒后子弹的速率为，则此时棒的角速
本章学习要点
1.角坐标、角位移、角速度、角加速度。 2.转动惯量、力矩，转动定律。 3.刚体转动的动能定理。 4.角动量定理、角动量守恒定律。
§4－1 刚体的平动与转动
1、角坐标、角速度、角加速度
P
角坐标 (t)
转动 o
平面
x
角速度 limd
t t0 dt
参考方向
角加速度 d
dt
2、角量与线量的关系
T1
T2
mAmBg mA mB
2）物体B 由静止出发作匀加速直线运动
v2 v02 2as
第二类问题：已知运动情况和力矩M ，求 J。
例：测轮子的转动惯量用一 M,R
根轻绳缠绕在半径为 R、质
量为 M 的轮子上若干圈后，
一端挂一质量为 m 的物体，
从静止下落 h 用了时间 t ,求
m
轮子的转动惯量 J。
dωdωdθ ω d ω
m,l FN
dt dθ dt d θ
θ
mg
3g
O
ωdω sinθdθ
2l
代入初始条件积分得 ω 3g(1cosθ)
l
或由能量守恒： mgL(1-co)s=1J2
2
2
得： ω 3g(1cosθ)
l
§4-3 角动量 角动量守恒定律
r
一、质点的角动量定理和角动量守恒定律
1、质点的角动量
第一类问题：已知J和力矩M ：求 和以及F。
书例2 质量为mA的物体A 静止在光滑水平面 上，和一质量不计的绳索相连接，绳索跨过一
半径R、质量mC的圆柱形滑轮C，并系在另一质 量为mB 物体B上，B 竖直悬挂．滑轮与绳索间 无滑动， 滑轮与轴承间的摩擦力可略去不计．
(1)两物体的线加速度为多少？ 水平和竖直两
掌握
1 刚体的角动量
LJ
2 刚体的角动量守恒定律
② 在冲击等问题中 M内M外L常量
பைடு நூலகம்子o
弹 击 入 杆
v
以子弹和沙袋为系统 动量守恒； 角动量守恒； 机械能不守恒 .
例1：光滑水平桌面上 有一长为 2L、质量为 m 匀质细杆，可绕其中点且垂直于杆的竖直光滑 固定轴自由转动，转动惯量 mL2/3， 起初杆静 止，桌面上有两个质量均为 m 的小球，各自在 垂直于杆的方向上，正对着杆的一端，以相同 速率 v 相向运动，当两个小球同时与杆的两个 端点发生完全非弹性碰撞后，与杆粘在一起转 动，则这一系统碰撞后的转动角速度应为:
W重090 Md
090mg2lcosd
1 mgl 2
m,l
mg
始末两态动能：
Ek
1J2
2
,
由动能定理： WEkEk0
Ek00
1mgl1J20
22
m,l
o
J 1 ml 2
3
3g
mg
l
小结
一、基本物理量
熟练掌握
L rm V
二、基本定理、定律
1、转动定律 2、动能定理
熟练掌握
3、角动量定理
h
P144作业 ４-11
受力分析：
m：m g Tma (1) M,R
M： T R J
(2)
T
物体从静止下落时满足
ha2t/2
aR
(3)
(4) T
h
mg J mR 2(g2t2h)
2h
书例3 一长为 l 、质量
为 m 匀质细杆竖直放置， 其下端与一固定铰链O相 接，并可绕其转动．由于 此竖直放置的细杆处于非
度应为
B
mv
(A) ML
3m v
(B) 2 ML
1 v
5m v
(C) 3 ML
(D) 7 m v
4 ML
2
O 俯视图
v
{B}
期中考题
直线运动与定轴转动规律对照
质点的直线运动
刚体的定轴转动
练习1：一细杆质量为m，
长度为l，一端固定在轴上， 静止从水平位置摆下，求
o
细杆摆到铅直位置时的角
速度。
解： 重力矩作功：
➢几个力同时作用，合力矩为
即：
合力矩的大小等于 各力矩的代数和。
F3 F2
F1
r2
r3
r1
二、转动定律
熟练掌握
MJ
J描述刚体转动惯性大小的物理量。 ❖ 质量离散分布
J m jr j 2 m 1 r 1 2 m 2 r 2 2 m jr j 2
❖ 质量连续分布
J mjrj2r2dmVr2dV j
三、转动定律应用举例 M J
1. 矢量式（定轴转动中力矩只有两个方向）；
2. 具有瞬时性且M、J、 是对同一轴而言的。
解题方法及应用举例
熟练掌握
1.确定研究对象。 2.受力分析（只考虑对转动有影响的力矩）。
3.列方程求解(平动物体列牛顿定律方程， 转动刚体列转动定律方程，并利用角量与线 量关系)。
段绳索的张力各为多少？
A
(2) 物体 B 从静止落下
mA
C
mC
距离 y 时，其速率是多少？
mB B
解：隔离法，受力分析
A
分别根据牛二定律和转动定律列方程：
角量、线量关系式
解得：
a
mBg
mAmBmC 2
T1
mAmBg mAmBmC
2
T2
(mAmC 2)mBg mAmBmC 2
如令 mC 0，可得：