下载文档原格式
统计学中的随机变量的分布与分位数概念在质量工程师的培训中，我们经常询问学员以下图形是什么曲线，学员普遍能够回答是正态分布曲线，但进一步询问学员该曲线的纵轴f(x)表示什么，许多同学以为是概率值。
其实这个曲线是正态分布概率密度曲线，f(x)是指随机变量X在观察值为x时的概率密度，如果随机变量X的单位为mm，则f(x)的单位为%/mm。
曲线与X轴所围成的面积表示概率，该面积等于1，因为随机变量的所有可能取值（即：100%）都在X轴上。
随机变量的分布与分位数概念以下是一个均值=10，标准差=0.5的正态分布概率密度曲线的例子，x=9.020的垂线与该分布的概率密度曲线和X轴所围成的左侧区域面积=0.025，该面积表示在随机变量X的总体分布中，有2.5%的值小于9.020，也就是说在总体分布中，随机变量X的取值小于9.020的概率为2.5%。
同样，x=10.98的垂线与该分布的概率密度曲线和X 轴所围成的右侧区域面积=0.025，该面积表示在随机变量X的总体分布中，有2.5%的值大于10.98，也就是说在总体分布中，随机变量X 的取值大于10.98的概率为2.5%（也即是随机变量X的取值小于10.98的概率为97.5%）。
在这个分布中，x=9.020的值被称为X的2.5%分位数（即：X2.5%=9.020），x=10.98的值被称为X的97.5%分位数（X97.5%=10.98）。
随机变量X有95%（即：97.5% -2.5%=95%）的取值落在9.020至10.98之间。
每个分位数都是随机变量所有可能取值中的某个值。
按照定义，若某个值Xp被称为随机变量X的p分位数，则随机变量X的取值小于Xp的概率为p。
随机变量的分布与分位数概念以下是该正态分布对应的累积概率分布曲线，该曲线的纵轴表示的是累积概率，比如：x=9.020对应的累积概率为2.5%（即：随机变量X的取值小于x=9.020的概率为2.5%）, x=10对应的累积概率为50%（即：随机变量X的取值小于x=10的概率为50%）, x=10.98对应的累积概率为97.5%（即：随机变量X的取值小于x=10.98的概率为97.5%）。
计算分位数的公式解释说明以及概述1. 引言1.1 概述在统计学和数据分析中，分位数是一种衡量数据集中趋势和分布的重要指标。
它用于将整个数据集划分为多个等比例的部分，并以此来描述数据的不同区间段内的特征。
计算分位数的公式是一种数学表达式，用于准确地计算某个给定数据集的各种分位数。
1.2 文章结构本文将首先介绍什么是分位数以及它在统计学中的应用。
其次，将解释和说明分位数的概念、意义以及与百分比之间的关系。
然后，我们会详细介绍常见的分位数计算公式，包括中位数和四分位数，并提供其他常用分位数公式及其应用场景举例。
最后，我们将总结文章中涉及到的主要观点和发现，并讨论计算分位数公式的重要性、局限性以及未来可能的研究方向。
1.3 目的本文旨在帮助读者更好地理解和应用计算分位数公式。
通过详细解释其意义、解读方法和具体计算步骤，读者可以对不同类型数据集中任意位置处所代表的具体含义有更清晰的认识。
此外，我们也将讨论计算分位数公式的重要性和局限性，以及未来可能的改进方向，以促进相关研究和应用的发展。
2. 计算分位数的公式：2.1 什么是分位数：分位数是统计学中常用的概念，用于描述和衡量数据集的分布情况。
它将数据集按照大小顺序划分为若干部分，从而得到具有统计意义的数值。
2.2 分位数的计算方法：要计算一个特定百分位数的值，可以按照以下步骤进行：- 将数据集按照大小顺序排列。
- 根据所需的百分位数确定相应的位置。
- 如果位置是整数，则对应位置上的值就是所需的百分位数。
- 如果位置不是整数，则需要进行插值计算，通常使用线性插值法或近似估计法。
2.3 分位数在统计学中的应用：分位数在统计学中有广泛的应用。
它可以用于描述数据集的中心趋势、离散程度以及异常值等方面。
常见的应用有以下几种情况：- 描述个体或群体收入和财富分布情况；- 衡量变量在某一区间内观测到的频率；- 在金融领域中对风险进行评估和管理；- 对股票市场进行技术分析；- 用于构建箱线图以检测离群值等。
分位数的概念分位数是指统计学中常用的一个概念，用来描述数据的分布情况。
它把一组数据分成几部分，每部分包含相同比例的数据。
分位数通常用来衡量数据的集中趋势和离散程度，是统计学和数据分析中非常重要的一个概念。
在统计学中，常用的分位数有四分位数、中位数和百分位数。
其中，四分位数又分为下四分位数（Q1）、中位数（Q2）和上四分位数（Q3）。
下四分位数是数据中25%的位置的值，中位数是数据中50%的位置的值，上四分位数是数据中75%的位置的值。
除了四分位数之外，还有百分位数，百分位数是指数据中有百分之几的观察值小于或等于它。
分位数的概念可以通过举例来更好地理解。
假设有一个班级的学生成绩数据，我们想要了解学生成绩的分布情况。
我们可以计算这组成绩的四分位数，从而找到25%、50%和75%位置的分数。
这样我们就可以得出学生成绩的集中趋势和离散程度。
比如，中位数可以帮助我们确定学生成绩的中间位置，四分位数可以帮助我们了解学生成绩中较低、中等和较高的位置，进而得出整体上学生成绩的分布情况。
分位数的计算方法有很多，最常用的是通过对数据进行排序，然后找到对应位置的数据点。
比如，要计算下四分位数，首先对数据进行排序，然后找到数据的25%位置的值即为下四分位数。
类似地，中位数和上四分位数也可以通过这种方法来计算。
分位数的应用非常广泛，它在数据分析、统计推断、风险管理等领域都有着重要的作用。
在数据分析中，分位数可以帮助我们了解数据的分布情况，发现异常值和离群点，寻找数据的集中趋势等。
在统计推断中，分位数可以用来构建置信区间、进行假设检验等。
在风险管理中，分位数可以用来衡量风险的不确定性和波动性，帮助决策者做出合理的决策。
此外，在金融领域中，分位数也有着重要的应用。
比如，价值-at-风险（Value-at-Risk，VaR）是衡量金融风险的一种常用方法，它主要通过计算分位数来对金融资产的风险进行评估。
总之，分位数是统计学中非常重要的一个概念，它可以帮助我们了解数据的分布情况，衡量数据的集中趋势和离散程度，对数据进行分析和推断，并在风险管理和决策中发挥重要作用。
分位数教学目标:1.理解分位数的概念2.会查表求常用统计分布的分位数教学内容：一、分位数的概念分位数或临界值与随机变量的分布函数有关，根据应用的需要，有三种不同的称呼，即α分位数、上侧α分位数与双侧α分位数，它们的定义如下：定义1：设随机变量X 的分布函数为()x F ，对于给定的实数α满足10<<α时，若有αx 满足(){}ααα=≤=x X P x F ，则称αx 为X 的α分位数；上侧α分位数是使{}()αλλ=-=>F X P 1的数λ，双侧α分位数是使{}()αλλ5011.F X P ==<的数1λ，使{}()αλλ50122.F X P =-=>的数2λ。
因为()()αλαλ-==-11F ,F ，所以上侧α分位数λ就是α-1分位数α-1x ；因为()()αλαλ5015021.F ,.F =-=，所以双侧α分位数1λ就是α50.的分位数α50.x ，双侧α分位数2λ就是α501.-分位数α501.x -。
二、几种常用统计分布的分位数1.标准正态分布的α分位数记作αu ，α50.分位数记作α50.u ，α501.-分位数记作α501.u -。
当X ～N(0,1)时，{}()ααα==<u F u X P 1,0，{}()ααα50501050.u F u X P .,.==<，{}()ααα50150110501.u F u X P .,.-==<--。
根据标准正态分布密度曲线的对称性，可知αα--=1u u 论述如下：当X ～N(0,1)时，{}()ααα==<u F u X P ,10， {}()ααα-==<--11101u F u X P ,，{}()ααα=-=>--11011u F u X P ,，故根据标准正态分布密度曲线的对称性，可知αα--=1u u 。
例如，u 0.10=-u 0.90=-1.282，u 0.05=-u 0.95=-1.645，u 0.01=-u 0.99=-2.326，u 0.025=-u 0.975=-1.960，u 0.005=-u 0.995=-2.576。
分位数教学目标:1.理解分位数的概念2.会查表求常用统计分布的分位数教学内容：一、分位数的概念分位数或临界值与随机变量的分布函数有关，根据应用的需要，有三种不同的称呼，即α分位数、上侧α分位数与双侧α分位数，它们的定义如下：定义1：设随机变量X 的分布函数为()x F ，对于给定的实数α满足10<<α时，若有αx 满足(){}ααα=≤=x X P x F ，则称αx 为X 的α分位数；上侧α分位数是使{}()αλλ=-=>F X P 1的数λ，双侧α分位数是使{}()αλλ5011.F X P ==<的数1λ，使{}()αλλ50122.F X P =-=>的数2λ。
因为()()αλαλ-==-11F ,F ，所以上侧α分位数λ就是α-1分位数α-1x ；因为()()αλαλ5015021.F ,.F =-=，所以双侧α分位数1λ就是α50.的分位数α50.x ，双侧α分位数2λ就是α501.-分位数α501.x -。
二、几种常用统计分布的分位数1.标准正态分布的α分位数记作αu ，α50.分位数记作α50.u ，α501.-分位数记作α501.u -。
当X ～N(0,1)时，{}()ααα==<u F u X P 1,0，{}()ααα50501050.u F u X P .,.==<，{}()ααα50150110501.u F u X P .,.-==<--。
根据标准正态分布密度曲线的对称性，可知αα--=1u u 论述如下：当X ～N(0,1)时，{}()ααα==<u F u X P ,10， {}()ααα-==<--11101u F u X P ,，{}()ααα=-=>--11011u F u X P ,，故根据标准正态分布密度曲线的对称性，可知αα--=1u u 。
例如，u 0.10=-u 0.90=-1.282，u 0.05=-u 0.95=-1.645，u 0.01=-u 0.99=-2.326，u 0.025=-u 0.975=-1.960，u 0.005=-u 0.995=-2.576。
统计学常用分布及其分位数1. 引言在统计学中，分布是指一组数据在各个取值上的分布情况。
统计学常用的分布包括正态分布、均匀分布、二项分布等。
而分位数是衡量分布上部分数据所占比例的一个指标，常用于描述数据的分布形状和集中程度。
本文将介绍统计学常用分布以及它们的分位数。
2. 正态分布及其分位数正态分布是统计学中最重要的分布之一，其分布曲线呈钟形。
它的分布的均值为μ，方差为σ^2。
正态分布的分位数可以通过查找标准正态分布表来获得。
常用的分位数包括：•第一四分位数（Q1）：将数据集分为四个部分，该分位数将数据集的前25%数据与后75%数据分开。
•第二四分位数（Q2）：也就是中位数，将数据集分为两个相等的部分。
•第三四分位数（Q3）：将数据集分为四个部分，该分位数将数据集的前75%数据与后25%数据分开。
3. 均匀分布及其分位数均匀分布是指在一段连续的数据区间内，各个数据点出现的概率是相等的。
均匀分布的分位数可以通过计算来获得。
常用的分位数包括：•下四分位数（Q1）：将数据集分为四个部分，该分位数将数据集的前25%数据与后75%数据分开。
•上四分位数（Q3）：将数据集分为四个部分，该分位数将数据集的前75%数据与后25%数据分开。
4. 二项分布及其分位数二项分布是常用的离散型分布，用于描述二分法试验在n次独立试验中成功的次数。
二项分布的分位数可以通过计算来获得。
常用的分位数包括：•下百分之P分位数：将数据集分为P%和(100-P)%两部分，下百分之P分位数将数据集的前P%数据与后(100-P)%数据分开。
5.本文介绍了统计学常用的分布及其分位数，分布的选取需要根据具体问题的特点来决定。
在实际应用中，通过计算或查表可以获得分布的分位数，从而对数据集的分布形状和集中程度有更深入的了解。
对于需要进行数据分析和统计推断的问题，了解常用分布及其分位数的特点和应用是非常重要的。
注意：本文只是对统计学常用分布及其分位数进行简要介绍，如需深入学习和应用，请参考相关的统计学教材和资料。
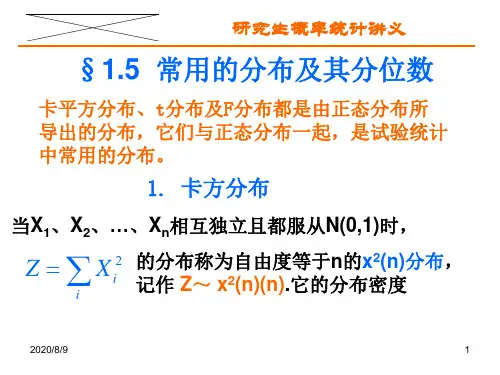
§1.4 常用的分布及其分位数1. 卡平方分布卡平方分布、t 分布及F 分布都是由正态分布所导出的分布，它们与正态分布一起，是试验统计中常用的分布。
当X 1、X 2、…、Xn 相互独立且都服从N(0,1)时，Z=∑ii X 2 的分布称为自由度等于n 的2χ分布，记作Z ～2χ(n)，它的分布密度 p(z )=⎪⎪⎩⎪⎪⎨⎧>⎪⎭⎫ ⎝⎛Γ--,,00,2212122其他z e x n z n n 式中的⎪⎭⎫ ⎝⎛Γ2n =u d e u u n ⎰∞+--012，称为Gamma 函数，且()1Γ=1，⎪⎭⎫ ⎝⎛Γ21=π。
2χ分布是非对称分布，具有可加性，即当Y 与Z 相互独立，且Y ～2χ(n )，Z ～2χ(m )，则Y+Z ～2χ(n+m )。
证明: 先令X 1、X 2、…、X n 、X n+1、X n+2、…、X n+m 相互独立且都服从N(0,1)，再根据2χ分布的定义以及上述随机变量的相互独立性，令Y=X 21+X 22+…+X 2n ，Z=X 21+n +X 22+n +…+X 2m n +，Y+Z= X 21+X 22+…+X 2n + X 21+n +X 22+n +…+X 2m n +，即可得到Y+Z ～2χ(n +m )。
2. t 分布 若X 与Y 相互独立，且X ～N(0,1)，Y ～2χ(n )，则Z =nY X 的分布称为自由度等于n 的t 分布，记作Z ～ t (n )，它的分布密度P(z)=)()(221n nn ΓΓ+2121+-⎪⎪⎭⎫ ⎝⎛+n n z 。
请注意：t 分布的分布密度也是偶函数，且当n>30时，t分布与标准正态分布N(0,1)的密度曲线几乎重叠为一。
这时， t 分布的分布函数值查N(0,1)的分布函数值表便可以得到。
3. F 分布 若X 与Y 相互独立，且X ～2χ(n )，Y ～2χ(m )， 则Z=mY n X的分布称为第一自由度等于n 、第二自由度等于m 的F 分布，记作Z ～F (n , m )，它的分布密度 p(z)=⎪⎪⎪⎩⎪⎪⎪⎨⎧>++-⎪⎭⎫ ⎝⎛Γ⎪⎭⎫ ⎝⎛Γ⎪⎭⎫ ⎝⎛+Γ•。
其他,00,2)(1222222z m n z n m n z m n m n m m n n 请注意：F 分布也是非对称分布，它的分布密度与自由度的次序有关，当Z ～F (n , m )时，Z1～F (m ,n )。
4. t 分布与F 分布的关系若X ～t(n )，则Y=X 2～F(1,n )。
证：X ～t(n )，X 的分布密度p(x )=⎪⎭⎫ ⎝⎛Γ⎪⎭⎫ ⎝⎛+Γ221n n n π2121+-⎪⎪⎭⎫ ⎝⎛+n n x 。
Y=X 2的分布函数F Y (y ) =P{Y<y }=P{X 2<y }。
当y ≤0时，F Y (y)=0，p Y (y )=0；当y >0时，F Y (y ) =P{-y <X<y } =x d x p y y )(⎰-=2x d x p y )(0⎰， Y=X 2的分布密度p Y (y )=21)(121221212n y n y n n n n ++-⎪⎭⎫ ⎝⎛Γ⎪⎭⎫ ⎝⎛Γ⎪⎭⎫ ⎝⎛+Γ•，与第一自由度等于1、第二自由度等于n 的F 分布的分布密度相同，因此Y=X2～F(1,n)。
为应用方便起见，以上三个分布的分布函数值都可以从各自的函数值表中查出。
但是，解应用问题时，通常是查分位数表。
有关分位数的概念如下：4. 常用分布的分位数1）分位数的定义分位数或临界值与随机变量的分布函数有关，根据应用的需要，有三种不同的称呼，即α分位数、上侧α分位数与双侧α分位数，它们的定义如下：当随机变量X的分布函数为F(x)，实数α满足0 <α<1 时，α分位数是使P{X< xα}=F(xα)=α的数xα，上侧α分位数是使P{X >λ}=1-F(λ)=α的数λ，双侧α分位数是使P{X<λ1}=F(λ1)=0.5α的数λ1、使P{X>λ2}=1-F(λ2)=0.5α的数λ2。
因为1-F(λ)=α，F(λ)=1-α，所以上侧α分位数λ就是1-α分位数x1-α；F(λ1)=0.5α，1-F(λ2)=0.5α，所以双侧α分位数λ1就是0.5α分位数x0.5α，双侧α分位数λ2就是1-0.5α分位数x1-0.5α。
2）标准正态分布的α分位数记作uα，0.5α分位数记作u 0.5α，1-0.5α分位数记作u1-0.5α。
当X～N(0,1)时，P{X< uα}=F 0,1(uα)=α，P{X<u0.5α}= F 0,1 (u0.5α)=0.5α，P{X<u1-0.5α}= F 0,1 (u1-0.5α)=1-0.5α。
根据标准正态分布密度曲线的对称性，当α=0.5时，uα=0；当α<0.5时，uα<0。
uα=-u1-α。
如果在标准正态分布的分布函数值表中没有负的分位数，则先查出 u1-α，然后得到uα=-u1-α。
论述如下：当X～N(0,1)时，P{X< uα}= F 0,1 (uα)=α，P{X< u1-α}= F 0,1 (u1-α)=1-α，P{X> u1-α}=1- F 0,1 (u1-α)=α，故根据标准正态分布密度曲线的对称性，uα=-u1-α。
例如，u 0.10=-u 0.90=-1.282，u 0.05=-u 0.95=-1.645，u 0.01=-u 0.99=-2.326，u 0.025=-u 0.975=-1.960，u 0.005=-u 0.995=-2.576。
又因为P{|X|< u1-0.5α}=1-α，所以标准正态分布的双侧α分位数分别是u1-0.5α和-u1-0.5α。
标准正态分布常用的上侧α分位数有：α=0.10，u 0.90=1.282；α=0.05，u 0.95=1.645；α=0.01，u 0.99=2.326；α=0.025，u 0.975=1.960；α=0.005，u 0.995=2.576。
χα(n)。
3）卡平方分布的α分位数记作2χα(n)>0，当X～2χ(n)时，P{X<2χα(n)}=α。
2χ0.005(4)=0.21，2χ0.025(4)=0.48，例如，2χ0.05 (4)=0.71，2χ0.95(4)=9.49，2χ0.975(4)=11.1，2χ0.995(4)=14.9。
24）t分布的α分位数记作tα(n)。
当X～t (n)时，P{X<tα(n)}=α，且与标准正态分布相类似，根据t分布密度曲线的对称性，也有tα(n)=-t1-α(n)，论述同uα=-u1-α。
例如，t0.95(4)=2.132，t 0.975(4)=2.776，t 0.995(4)=4.604，t 0.005(4)=-4.604，t 0.025(4)=-2.776，t 0.05(4)=-2.132。
另外，当n>30时，在比较简略的表中查不到tα(n)，可用uα作为tα(n)的近似值。
5）F分布的α分位数记作Fα(n , m)。
Fα(n , m)>0，当X～F (n , m)时，P{X<Fα(n , m)}=α。
另外，当α较小时，在表中查不出F α(n , m )，须先查F 1-α(m , n )，再求F α(n , m )=),(11n m F α-。
论述如下： 当X ～F(m , n )时，P{X< F 1-α(m , n )}=1-α， P{X 1>),(11n m F α-}=1-α，P{X 1<),(11n m F α-}=α， 又根据F 分布的定义，X 1～F(n , m )，P{X 1<F α(n , m ) }=α， 因此 F α(n , m )= ),(11n m F α-。
例如，F 0.95 (3,4)=6.59，F 0.975 (3,4)=9.98，F 0.99 (3,4)=16.7，F 0.95 (4,3)=9.12，F 0.975 (4,3)=15.1，F 0.99 (4,3)=28.7，F 0.01 (3,4)=7.281，F 0.025 (3,4)=1.151，F 0.05 (3,4)=12.91。
【课内练习】1. 求分位数①0.05(8)，②0.95(12)。
2. 求分位数① t 0.05(8)，② t 0.95(12)。
3. 求分位数①F0.05(7,5)，②F0.95(10,12)。
4. 由u 0.975=1.960写出有关的上侧分位数与双侧分位数。
5. 由t 0.95(4)=2.132写出有关的上侧分位数与双侧分位数。
6. 若X～(4)，P{X<0.711}=0.05，P{X<9.49}=0.95，试写出有关的分位数。
7. 若X～F(5,3)，P{X<9.01}=0.95，Y～F(3,5)，{Y<5.41}= 0.95，试写出有关的分位数。
8. 设X、X、…、X相互独立且都服从N(0,0.09)分布,试求P{>1.44}。
习题答案：1. ①2.73，②21.0。
2. ①-1.860，②1.782。
3. ①，②3.37。
4. 1.960为上侧0.025分位数，-1.960与1.960为双侧0.05分位数。
5. 2.132为上侧0.05分位数，-2.132与2.132为双侧0.1分位数。
6. 0.711为上侧0.95分位数，9.49为上侧0.05分位数，0.711与19.49为双侧0.1分位数。
7. 9.01为上侧0.05分位数，5.41为上侧0.05分位数，与5.41为双侧0.1分位数，与9.01为双侧0.1分位数。
8. 0.1。
